
信号処理の分野では2つの信号の関係を周波数領域で分析するために周波数応答関数という計算を多用します。Pythonでフーリエ変換が出来るようになったらあと一歩なので、ここではPythonによる周波数応答関数の計算方法を紹介します。
こんにちは。wat(@watlablog)です。ここではPythonを使って信号処理の重要計算である周波数応答関数を求めてみます!
周波数応答関数の概要
伝達関数?周波数応答関数?
機械系でも電気系でも、実物でもシミュレーションモデルでも、開発系の仕事をしている人であればあるシステムに何らかの信号を入力したときの出力を分析することが多いと思います。
僕は機械系なので構造物で例えますが、以下のようにある物体を任意の力[\(\rm N\)]で加振させ、その物体の加速度応答[\(\rm m/s^{2}\)]との比を評価することがよくあります。
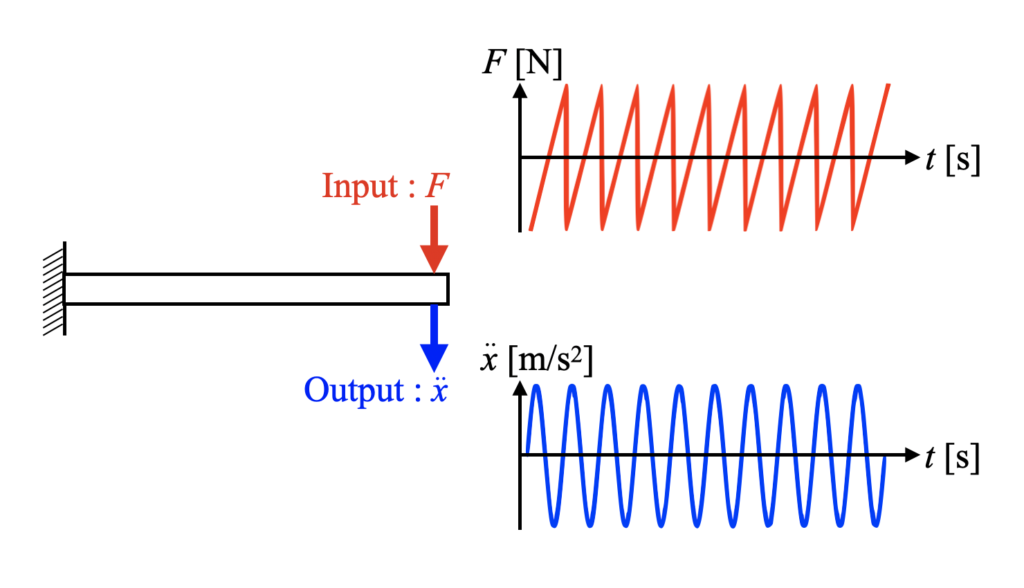
ここで、力や加速度、他にも速度や変位、ひずみや応力といった物体の状態を決定することができる量を状態量(State value)と呼び、これらの状態量を使って入力と出力の比をとったものを伝達関数(Transfer function)と呼びます。
この伝達関数の独立変数に周波数をとったものを特に周波数応答関数(FRF:Frequency Response Function)と呼びます。
実際に使う時は、単にFRFと呼ぶことが多いですね。
この周波数応答関数からは様々な情報を得ることが出来ます。ではその目的を探ってみましょう。
FRFは入力と出力の関係を分析するために計算する
先ほど図示した、入力である加振力と応答である加速度の波形は、波の形も異なるので、一見するだけでは2信号間にどのような関係があるのかを調べることは困難です。
振動している信号の分析としてはフーリエ変換を使って周波数や振幅、位相を調べることがよくありますが、それぞれの信号を別々にフーリエ変換した所で、2信号間の関係性を分析することは依然として困難なままです。
そこで、FRFの出番となります。
FRFを計算することで、
・入力の振幅に対して応答の振幅がどれだけ出たか?
・入力に対して応答はどれだけ遅れて発生したか?
…といった情報が一目瞭然となります。
さらに、それらの情報からシステムがどのような振動モードを持っているかを同定する実験モーダル解析が出来たり、プロットを工夫して共振点の評価にどれだけ誤差を含んでいるかといった分析も可能となります。
いろんな物理分野の分析に大変重宝するため、是非覚えてみましょう!
周波数応答関数の式
先ほど文章で説明した通り、入力\(I\)と出力\(O\)の比である伝達関数\(H\)で周波数\(f\)(または角振動数\(\omega \))を考慮すれば良いので、FRFは以下の式(1)で定義されます。
\[
H(\omega )=\frac{O(\omega )}{I(\omega )} \tag{1}
\]
ここで、\(I(\omega ), O(\omega )\)は共に複素数です。
一般に入力と出力の各信号は共に位相情報も周波数の関数であるので、式(2)と分母を実数にするために共役複素数\(I^{\star}(\omega )\)(複素数の虚部に-1を乗じたもの、1+2jであれば共役複素数は1-2j)を分母分子に乗じます。
\[
H(\omega )=\frac{O(\omega )I^{\star}(\omega )}{I(\omega )I^{\star}(\omega )} \tag{2}
\]
ちなみに、分母の\(I(\omega )I^{\star}(\omega )\)はパワースペクトル(Power spectrum)、分子の\(O(\omega )I^{\star}(\omega )\)はクロススペクトル(Cross spectrum)と呼ばれます。
クロススペクトル単体は2信号間の相関や位相差を分析する時に使われますが、FRFの振幅成分は入出力の比、位相成分は入出力の差を意味する関数であるとわかります。
周波数応答関数の代表例
機械系でよく使われるFRFの呼称と単位を下表に示します。参考までに。
| 呼称 | 単位 |
| コンプライアンス(Compliance) | [\(\rm m/N\)] |
| モビリティ(Mobility) | [\(\rm m/(Ns)\)] |
| アクセレランス(Accelerance) | [\(\rm m/(Ns^{2})\)] |
| 動剛性(Dynamic stiffness) | [\(\rm N/m\)] |
| 機械インピーダンス(Mechanical impedance) | [\(\rm Ns/m\)] |
| 動質量(Apparent mass) | [\(\rm Ns^{2}/m\)] |
参考文献
周波数応答関数については、以下の「モード解析入門」に式(P198くらい)や理論的背景が詳しく書いてあります。本書は振動学を学ぶ人必携の書と思いますので、是非書店等で見てみて下さい。
さて、式が出て概要がわかってきたので、早速Pythonによるコーディングをしていきましょう!
PythonでFRFを計算するコード
高速フーリエ変換(FFT)についてのおさらい
今回はフーリエ変換を既にPythonで使えるものとして話を進めますが、フーリエ変換の概要、計算上の注意点、Pythonコードについては過去に書いた「PythonでFFT!SciPyのFFTまとめ」をご覧下さい。
しかし上記記事はやや複雑な処理を複数使っています。本記事では窓関数やオーバーラップ処理は使わず、最も簡易なフーリエ変換を使ってコーディングします。
上記記事の説明は前提として、コード自体は「PythonでFFTとIFFT!逆フーリエ変換で時間波形を作る」で紹介したものを流用したいと思います。
準備:サンプルの信号を用意する
FRFの計算確認で適当に用意した信号を使うとあまり面白くありません。
ここでは出来るだけ物理的に値を確認できるよう、「工学カテゴリ」で学んだ振動モデルを使います。
シミュレーションモデル
モデルは以下に示す2自由度のばねマスダンパー系を用意しました。強制加振を入力、\(x_{2}\)の変位応答をとってFRFを計算します。
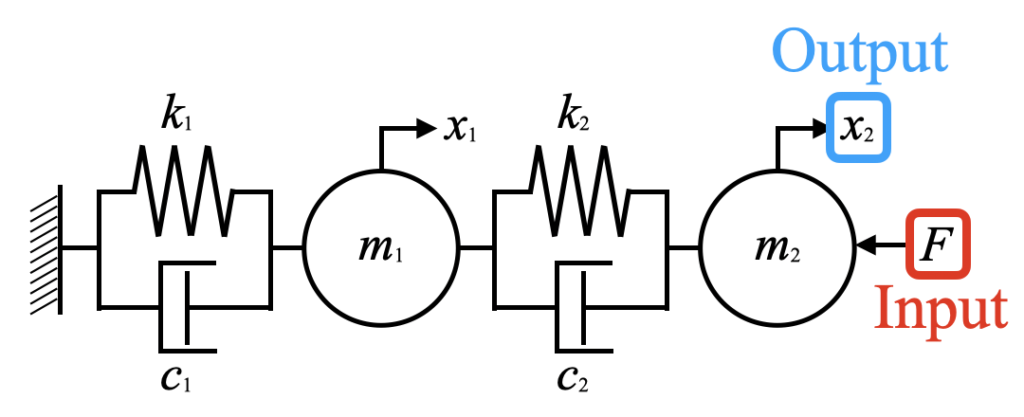
このモデルの運動方程式は式(3)です。全て行列、ベクトル形式で書いています。
\[
\mathbf{M}\mathbf{\ddot{x}}+\mathbf{C}\mathbf{\dot{x}}+\mathbf{K}\mathbf{x}=\mathbf{F} \tag{3}
\]
数値計算コードを別途.pyファイルで作成しておく
まずは上記運動方程式を数値解析するコードを「simulation.py」というファイルで作成します。
このコードは「Pythonの4次ルンゲ・クッタ法で多自由度連成振動を解く方法」でやった時とほとんど同じですが、外力をランダム加振とするために予め外力の離散1D配列を作っておく所、メインの計算実行文もdef関数にしている所が異なります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 |
import numpy as np # 運動方程式を関数として定義 def f(x, v, f): # 質量・減衰・剛性の集中定数を設定する m1 = 0.1 m2 = 0.05 c1 = 0.6 c2 = 0.3 k1 = 50.0 k2 = 40.0 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) M_inv = np.linalg.inv(M) # 質量マトリクスの逆行列 F = np.array([[0.0], [f]]) # 外力ベクトル # 減衰強制振動モデル y = np.dot(M_inv, F) - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y # シミュレーションを4次のRunge-Kutta法で実行する関数 def sim(): # 解析条件 t0 = 0.0 # 開始時間 t1 = 50.0 # 終了時間 dt = 1e-2 # 時間刻み # 初期条件 x0 = np.array([[0.0], [0.0]]) # 初期変位[m] v0 = np.array([[0.0], [0.0]]) # 初期速度[m/s] x, v = x0, v0 # 初期値に設定 t_axis = np.arange(t0, t1, dt) # 時間軸 x_sol = [] # 初期化x(変位)配列 v_sol = [] # 初期化v(速度)配列 # ガウシアンノイズを加振力に設定 force = 1.0 * np.random.normal(loc=0, scale=1, size=len(t_axis)) # 4次のRunge-Kutta法による数値解析(外力成分を離散1D波形から抽出するバージョン) iteration = 0 for t in t_axis: x_sol.append(x[1, 0]) # 2つ目の自由度の変位を結果として抽出 v_sol.append(v[1, 0]) # 2つ目の自由度の速度を結果として抽出 print('iteration=', iteration,'time=', t, force[iteration]) k11 = f(x, v, force[iteration]) * dt k12 = v * dt k21 = f(x + dt / 2, v + k11 / 2, force[iteration]) * dt k22 = (v + k11 / 2) * dt k31 = f(x + dt / 2, v + k21 / 2, force[iteration]) * dt k32 = (v + k21 / 2) * dt k41 = f(x + dt, v + k31, force[iteration]) * dt k42 = (v + k31) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 iteration += 1 return force, x_sol, dt, t_axis |
メイン:PythonでFRFを計算するコード
ボード線図を描いてみる
以下がメインの.pyファイルの内容です(グラフ化まで含んでいるので少々長いですが)。こちらのメインファイルの方には、FRF計算部分のみを関数にし、先ほどのsimulation.pyをimportしてサンプル信号を生成、その信号を使ってFRFを算出するという流れです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt import simulation # 周波数応答関数(FRF)を計算する関数 def frf(input, output, samplerate): fft_i = fftpack.fft(input) # 入力信号のフーリエ変換 fft_o = fftpack.fft(output) # 出力信号のフーリエ変換 # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) # FRFの振幅成分 amp = amp / (len(input) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(h_io.imag, h_io.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(input)) # 周波数軸を作成 return h_io, amp, phase, freq # サンプル信号を準備する(別ファイルで作成したsimulation.pyのsim()関数で計算) input, output, dt, t_axis = simulation.sim() # FRFを関数を実行して計算 h_io, amp, phase, freq = frf(input, output, 1 / dt) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(222) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(224) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') # スケールの設定をする。 ax3.set_xticks(np.arange(0, 20, 2)) ax3.set_xlim(0, 10) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax4.set_xticks(np.arange(0, 20, 2)) ax4.set_xlim(0, 10) ax4.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='Input', lw=1, color='red') ax2.plot(t_axis, output, label='Output', lw=1, color='blue') ax3.plot(freq, phase, lw=1) ax4.plot(freq, amp, lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
以下が結果です。左の2プロットが入力としてのランダム加振力、変位の時間波形です。そして右の2プロットが周波数応答関数の振幅(下)と位相(上)です。
振幅と位相を縦にプロットしたグラフをボード線図(Bode plot)と呼び、一般的に広く使われている描画方法です。
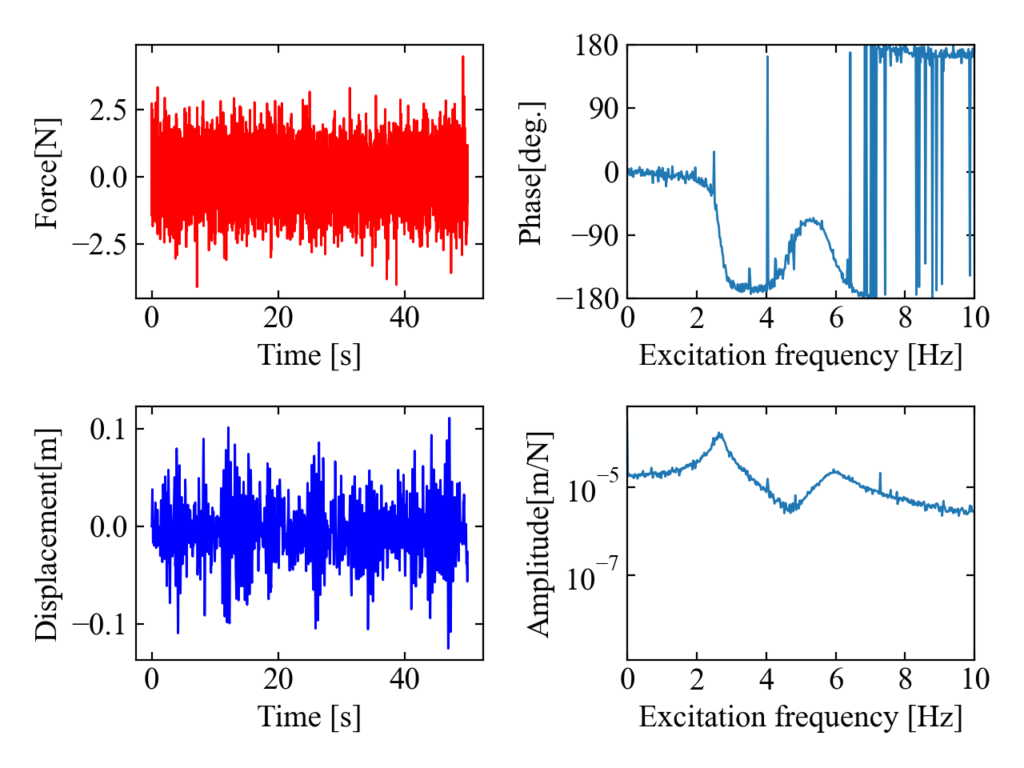
2自由度なので、振幅にはピークが2つ確認出来ます。そして振幅でピークが見える周波数には位相が90[deg.](力と変位の関係なので)になっています。
このくらいの検証しかしていませんが、モード理論通りなのでうまくいっていると考えます。
コクアド線図を描いてみる
以上でFRFの目的はおおよそ達成したのですが、他にも有用なプロット方法があるため、Pythonで再現してみたいと思います。最初はコクアド線図です。
コクアド線図は共振のピークがボード線図よりも急峻であることから、共振判別の1つの方法として使われます(あまり一般的には見ませんが)。
この線図は横軸に周波数をとり、縦軸に実部と虚部を並べます。英語でCoincident quadrature plotとなるため、Co. quad. plotとなります。
コードはグラフプロット部分のみを以下のように変更します。FRF計算関数には予め実部と虚部が入ったh_ioも出力しているのでこの部分だけでOKです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
# ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(222) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(224) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Re[m/N]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Im[m/N]') # スケールの設定をする。 ax3.set_xticks(np.arange(0, 20, 2)) ax3.set_xlim(0, 10) ax4.set_xticks(np.arange(0, 20, 2)) ax4.set_xlim(0, 10) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='Input', lw=1, color='red') ax2.plot(t_axis, output, label='Output', lw=1, color='blue') ax3.plot(freq, h_io.real, lw=1) ax4.plot(freq, h_io.imag, lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
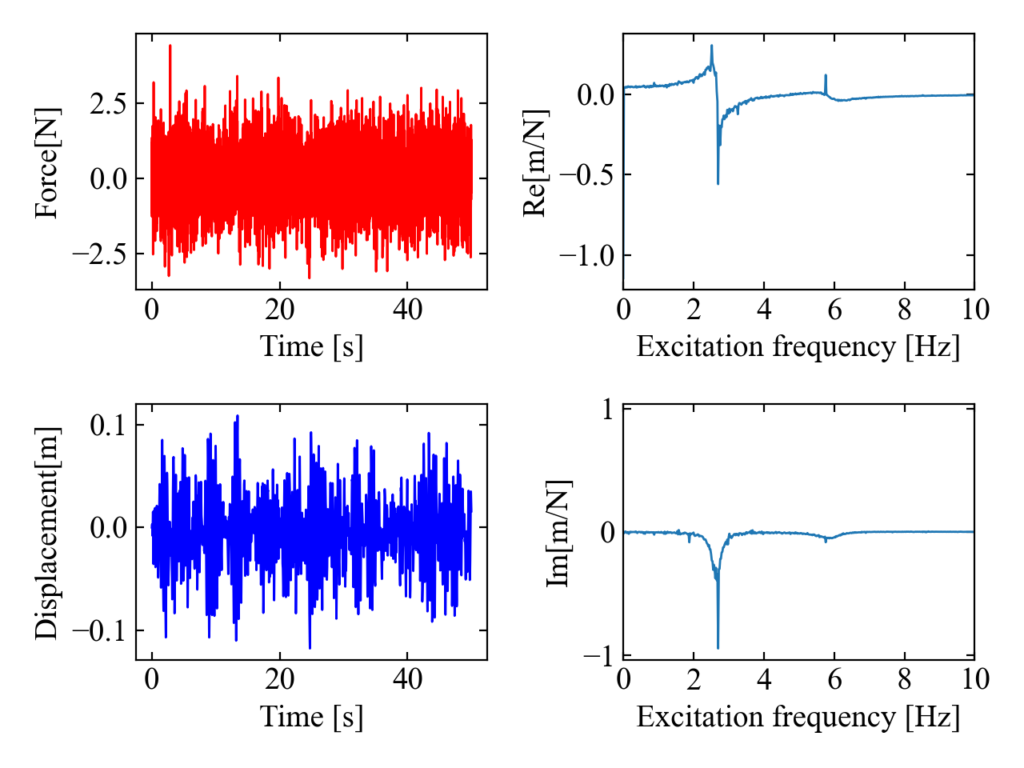
以下がコクアド線図の結果です。実部(Re)と虚部(Im)で急峻なピークが確認出来ました。
ナイキスト線図を描いてみる
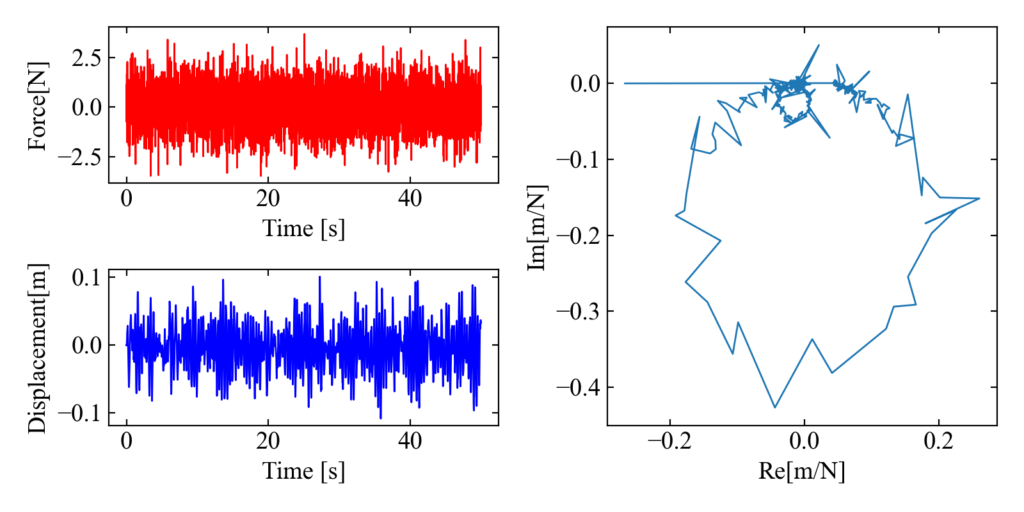
次はナイキスト線図(Nyquist plot)です。このナイキスト線図は横軸に実部、縦軸に虚部をとってプロットする図で、共振部分だけにフォーカスした図になり、1つの図だけ見れば良いというメリットがあるのでコクアド線図よりは使われているイメージです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(8, 4)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Re[m/N]') ax3.set_ylabel('Im[m/N]') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='Input', lw=1, color='red') ax2.plot(t_axis, output, label='Output', lw=1, color='blue') ax3.plot(h_io.real[0: int(len(h_io)/2)], h_io.imag[0: int(len(h_io)/2)], lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
以下がナイキスト線図のプロット結果です。実部と虚部の値が共振部分で円を描くというプロットです…が、シミュレーションと言ってもランダムノイズを加振に使用しているからか、ちょっといびつな形状をしていますね。ナイキスト線図は円の綺麗さから非線形性や誤差の割合を俯瞰できるため、実験でよく使われていますかね。
まとめ
本記事では周波数応答関数(FRF)の概要を説明し、定義式や機械系で代表的なFRFの種類を紹介しました。
また、PythonによるFRF算出コードを紹介し、実際にシミュレーションモデルを使った事例としてボード線図、コクアド線図、ナイキスト線図をそれぞれ紹介しました。
FRFは実験やシミュレーションで分野を問わず頻繁に使われる強力な信号分析手法です。是非本ページのコードを参考にしてみて下さい。
FRFを覚えたので周波数分析の幅がひろがりました!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント