
教師なし学習であるクラスタリングにはk-means法という手法があります。ここではk-means法のアルゴリズム概要を説明し、簡単に計算が可能なscikit-learnを使ったPythonによるサンプルコードを紹介します。
こんにちは。wat(@watlablog)です。本日はクラスタリングの基礎!k-means法の概要とPythonコードを紹介します!
k-means法によるクラスタリング概要
k-means法とは?
k-means法とは、クラスタリングを行うアルゴリズムの1つで教師なし学習法の中の一手法でもあります。
当ブログでは過去に、
・決定木による分類
・ランダムフォレストによる分類
・ロジスティック回帰による分類
・サポートベクターマシンによる分類
・サポートベクターマシンによる回帰
・k近傍法による分類
…と、様々な機械学習手法を紹介してきましたが、これらのどれもが教師あり学習でした。
教師あり学習とは、トレーニングデータと呼ばれる正解データを用いて学習を行う手法で、分類問題であればデータと紐付けになっているクラスラベル、回帰問題であればデータの値自体が目指すべき正解になります。
一方教師なし学習とは、トレーニングデータを使わない、つまり正解がない状態からデータの本質的な構造を抽出する手法です。
代表例としてクラスタリング(クラスター分析)が挙げられます。
他には統計の分野でよく聞く主成分分析とかも教師なし学習の1つとされていますね。
クラスタリングとは、データ群から特徴的な構造を抽出してデータを複数のクラスタ(まとまり)に分けることを意味します。
例えば、以下のような2変数で表現されたプロットがあるとしましょう。
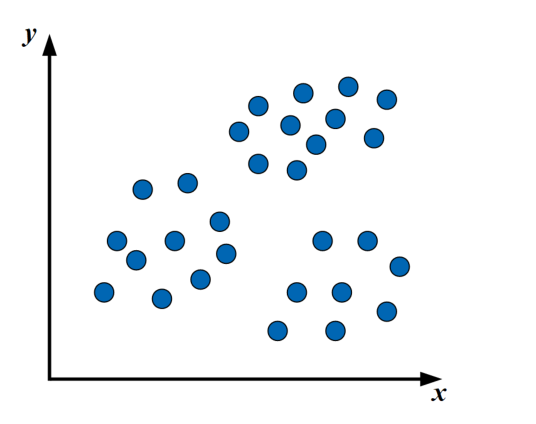
僕達人間の目で見ると、「なんとなく」…
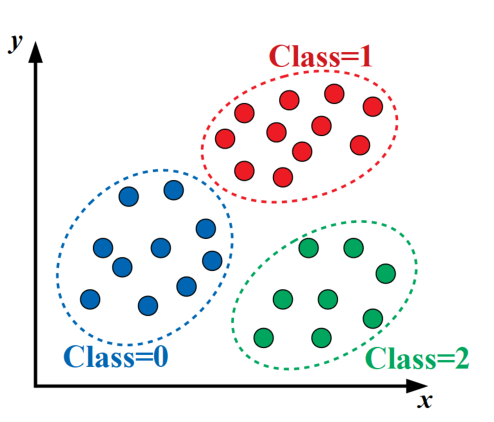
…このように分かれているような気がしませんか?(しない?)
感覚はさておき、上図のようにデータ群をあるルールに沿ってグルーピングするのがクラスタリングです。
k-means法とは、このいくつかのクラスタをk個と設定し、データの重心を探索しながら分類していく方法です。
言葉では中々イメージが湧かないと思いますので、まずはイメージを付けましょう!
k-means法の手順(numpyコードで解説)
動画でk-means法の手順を理解しよう!
ざっくりとした手順を直感的に理解するためには、言葉よりも動画の方が効率が良いと思いましたので、以下にYoutubeにアップロードしたk-means法のプロセス可視化動画を示します。
それではこれから動画の内容詳細を説明していきます。
①k個のクラスタ中心をランダムに生成する
まず始めに、k-means法のハイパーパラメータであるクラスタ数\(k\)を設定します。
最初は特に情報が無いので、データ群上にランダムに\(k\)個の点を置きます。
※次元数が増えても考え方は同じです。
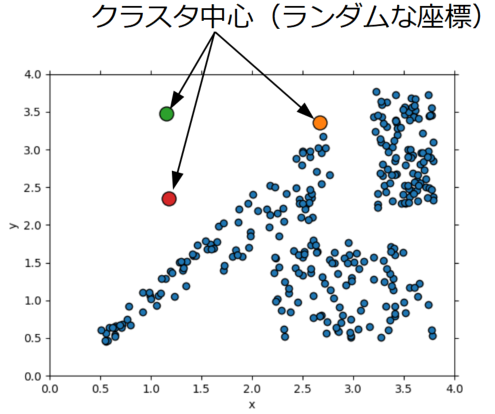
この点は本来クラスタの中心を意味する点となりますが、最初はとても中心には見えません。
②各データを最も近いクラスタに属するようにする
次に、各データとそれぞれのクラスタ中心との距離を計算して、各データと最も近いクラスタと関連をつけます(ここでは黒い線で表現しています)。
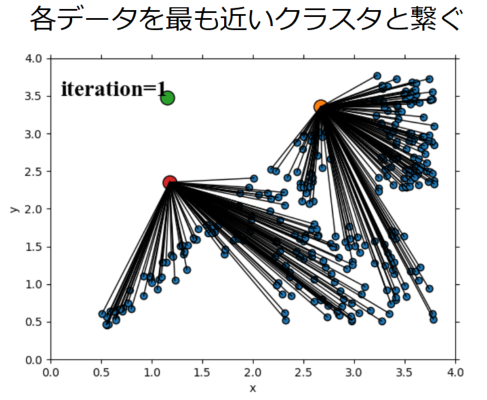
クラスタ中心はランダムな点を使っているので、中にはどの点から見ても遠い点となる場合もありますがこの点は次に再度ランダムに決定します。
③クラスタ中心をデータの重心に移動させる
仮でもデータとクラスタ中心を関連付けした後は、クラスタ中心を自身のデータ群の重心(平均)に移動させます。この時に平均計算をしていることがk-means法(k平均法)の由来になります。
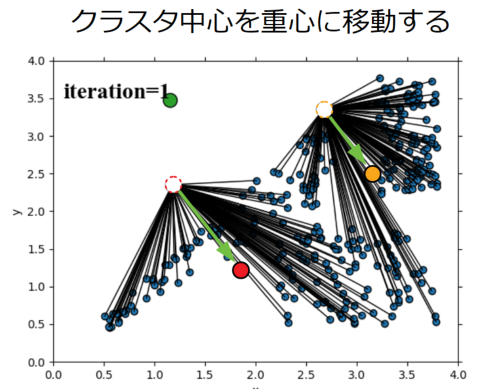
④データを再度クラスタと繋ぎ直す
クラスタ中心をデータ群の重心に移動させた後は、データとクラスタ中心の距離関係が変わってしまうので再度距離計算をし直し関連付けを更新します。
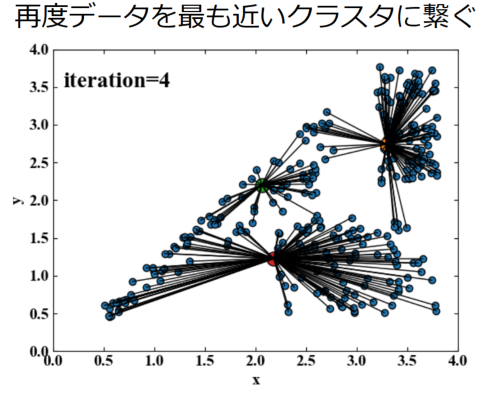
先ほどどのデータとも距離が遠かった点も、何度かランダム生成を繰り返すとそのうちどこかのデータに繋がります。
⑤クラスタ中心が動かなくなるまで繰り返す
上記計算をクラスタの中心が動かなくなるまで、具体的には移動量があるトレランスを下回るまで繰り返します。
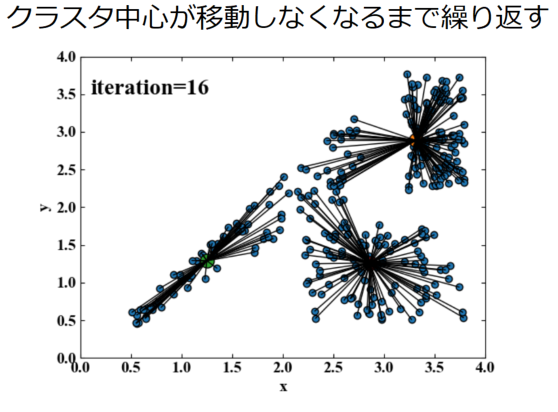
以下が最終的に得られたデータのクラスです。ちょっとオシイ気もしますが、特に正解ラベルがなくても単純なアルゴリズムでここまで分類することができました。
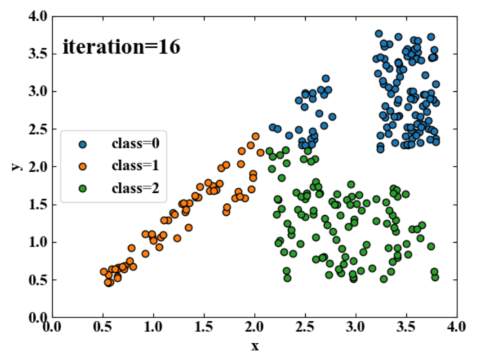
おまけ:numpyによるk-means法コード
先ほどまでの図はPythonのnumpyを使ってコーディングしたk-means法(細かい所を見ると、厳密には違うかも知れませんが)からプロットを画像にしていったものです。
\(xy\)データ限定のコードですが、参考までに以下に全コードを記載します。このコードを実行すると計算を実行した.pyファイルがあるフォルダに各イタレーションの画像がナンバリングされて保存されていきます。
コードの内容はコード内のコメントをご覧下さい。是非多変数へ対応した一般化をしたり、いじって遊んでみて下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
import numpy as np import pandas as pd from matplotlib import pyplot as plt # データを用意する(クラスタリングするためラベルは全て0)------ df = pd.DataFrame() n = 100 for i in range(3): if i == 0: x = pd.Series(np.random.uniform(0.5, 2.8, n)) y = pd.Series(x * np.random.uniform(0.8, 1.2, n)) elif i == 1: x = pd.Series(np.random.uniform(2.2, 3.8, n)) y = pd.Series(np.random.uniform(0.5, 1.8, n)) else: x = pd.Series(np.random.uniform(3.2, 3.8, n)) y = pd.Series(np.random.uniform(2.2, 3.8, n)) label = pd.Series(np.full(n, 0)) temp_df = pd.DataFrame(np.c_[x, y, label]) df = pd.concat([df, temp_df]) df.index = np.arange(0, len(df), 1) # ---------------------------------------------------------- convergence = False # 収束判定変数 tolerance = 0.001 # トレランス img_count = 0 # プロット保存枚数 iteration = 0 # イタレーション回数 k = 3 # クラスタ数 x = np.zeros(k) # クラスタ数でx座標を初期化 y = np.zeros(k) # クラスタ数でy座標を初期化 while convergence == False: # グラフ描画初期化------------------------------------------ fig = plt.figure() ax1 = plt.subplot(111) # データをプロットする ax1.scatter(df[0], df[1], label='class=0', edgecolors='black') # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 4) ax1.set_ylim(0, 4) # ---------------------------------------------------------- # 初期のクラスタ中心をランダムで用意する for j in range(k): if iteration == 0: x[j] = np.random.uniform(df[0].min(), df[0].max(), 1) # データのx範囲内でランダム値を与える y[j] = np.random.uniform(df[1].min(), df[1].max(), 1) # データのx範囲内でランダム値を与える ax1.scatter(x[j], y[j], edgecolors='black', s=150) if iteration == 0: img_count += 1 plt.savefig('fig' + str("{:05}".format(img_count)) + '.png') iteration += 1 # データを最も近いクラスタに振り分ける for m in range(len(df[0])): # データ行数分のループを回す distance = np.zeros(k) # 距離変数を初期化 for n in range(k): # クラスタ数分のループを回す line_data = df.iloc[m] # 1行抽出 xd = line_data[0] # データ点のx座標 yd = line_data[1] # データ点のy座標 distance[n] = np.sqrt((xd-x[n])**2 + (yd-y[n])**2) # クラスタ中心までの距離を計算 if n == k-1: # クラスタ数分距離を計算したら実行 df.iloc[m, 2] = np.argmin(distance) # データとクラスタ中心の距離が最小となる指標で分類 ax1.plot([xd, x[np.argmin(distance)]], [yd, y[np.argmin(distance)]], color='k', linestyle='-', linewidth=1) sum_convergence = 0 # 収束判定したかどうかをk個カウントする変数 for o in range(k): class_data = df[df[2] == o] # データフレームから1クラスタ分のデータを抽出 x_mean = class_data[0].mean() # 抽出したデータのx平均を算出 y_mean = class_data[1].mean() # 抽出したデータのy平均を算出 x_residue = np.sqrt((x_mean - x[o]) ** 2) # xデータの平均とクラスタ中心の二乗誤差(残差)を算出 y_residue = np.sqrt((y_mean - y[o]) ** 2) # yデータの平均とクラスタ中心の二乗誤差(残差)を算出 print(x_residue, y_residue) # 残差を表示 # ランダムなクラスタ中心がどのデータとも遠い場合はNaNになるので、NaNの場合は再度ランダム中心を算出する if np.isnan(x_mean) or np.isnan(y_mean): x_mean = np.random.uniform(df[0].min(), df[0].max(), 1) y_mean = np.random.uniform(df[1].min(), df[1].max(), 1) # xとy残差の両方がトレランス以下であればこのクラスタは収束 if x_residue <= tolerance and y_residue <= tolerance: sum_convergence += 1 else: x[o] = x_mean y[o] = y_mean # 全てのクラスタが収束(sum_convergence == k)したら収束判定をTrueにする if sum_convergence == k: convergence = True plt.text(0.1, 3.5, 'iteration=' + str(iteration), fontsize=20) img_count += 1 plt.savefig('fig' + str("{:05}".format(img_count)) + '.png') # おまけ:データをクラス毎に色分けしてグラフに描画する # グラフ描画初期化------------------------------------------ fig = plt.figure() ax1 = plt.subplot(111) # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 4) ax1.set_ylim(0, 4) # データをプロットする class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 class_2 = df[df[2] == 2] # ラベル2を抽出 ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') ax1.scatter(class_2[0], class_2[1], label='class=2', edgecolors='black') plt.legend(loc='center left') plt.text(0.1, 3.5, 'iteration=' + str(iteration), fontsize=20) img_count += 1 plt.savefig('fig' + str("{:05}".format(img_count)) + '.png') # ---------------------------------------------------------- |
Python/scikit-learnによるk-means法コード
全コード
先ほどまではアルゴリズムの理解を深めるためにあえて車輪の再発明をしてみましたが、Pythonには先人が積み上げた知識をライブラリにした外部パッケージがあるので、通常はこれを使います。
ここではscikit-learnという機械学習ライブラリを使ってk-means法によるクラスタリングをしてみます。
以下がscikit-learnによるk-means法のサンプルコードです。
サンプルデータ生成やグラフ表示部分を除けば、クラスタリング部分はわずか数行です。
k-means法を使うために、from sklearn.cluster import KMeansを宣言します。KMeansのn_clustersでクラスタ数\(k\)を指定しています。
.fit_predictを使うことで配列としてクラス分類結果を受け取ることができ、この配列をpandasデータフレーム置換したものが最終的なアウトプットです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
from sklearn.cluster import KMeans import numpy as np import pandas as pd from matplotlib import pyplot as plt # データを用意する(クラスタリングするためラベルは全て0)------ df = pd.DataFrame() n = 100 for i in range(3): if i == 0: x = pd.Series(np.random.uniform(0.5, 2.8, n)) y = pd.Series(x * np.random.uniform(0.8, 1.2, n)) elif i == 1: x = pd.Series(np.random.uniform(2.2, 3.8, n)) y = pd.Series(np.random.uniform(0.5, 1.8, n)) else: x = pd.Series(np.random.uniform(3.2, 3.8, n)) y = pd.Series(np.random.uniform(2.2, 3.8, n)) label = pd.Series(np.full(n, 0)) temp_df = pd.DataFrame(np.c_[x, y, label]) df = pd.concat([df, temp_df]) df.index = np.arange(0, len(df), 1) # ---------------------------------------------------------- data = df[[0, 1]] # データフレームからxyを抜き出す # k-means法によるクラスター分析 clf = KMeans(n_clusters=3) # k-meansモデルを定義 cluster = clf.fit_predict(data) # クラスター分析(分類結果が出力される) df.iloc[:, 2] = pd.Series(cluster) # 分類結果をデータと関連付ける class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 class_2 = df[df[2] == 2] # ラベル2を抽出 # ここからグラフ描画---------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' fig = plt.figure() ax1 = plt.subplot(111) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 4) ax1.set_ylim(0, 4) # データプロットする。 ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') ax1.scatter(class_2[0], class_2[1], label='class=2', edgecolors='black') plt.legend() # グラフを表示する。 plt.show() plt.close() # ---------------------------------------------------------- |
実行結果
以下が上記コードの実行結果です。先ほど自作したnumpy版の結果とほぼ一致した結果を得ることができました(データはランダム生成なので若干違うのは仕方ない)。
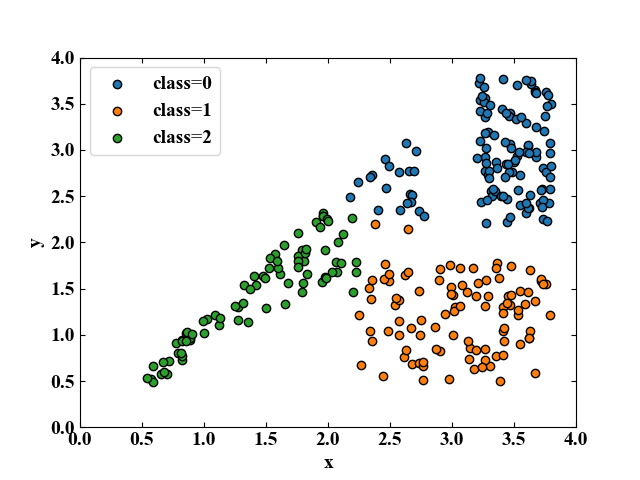
k-means法はデータが広く分布(分散が大きい)しているとうまくクラスタリングしてくれないような結果ですね。これを解決する別のアルゴリズムとかもあるのかな?
Twitterでは混合ガウスモデルはどうか?とアドバイスを頂きました!別手法についてはまたの機会にまとめようと思います!
まとめ
本ページでは教師なし学習の1つであるk-means法によるクラスタリングの概要を説明しました。
説明にはライブラリを利用するだけでなく、あえてnumpyで2変数の場合のクラスタリングを実装してみることで理解を深めることに挑戦しました。
実際にコーディングし、動画でk-means法のプロセスを眺めているとどのような変化をしているのかが一目瞭然でした。
また、最後にscikit-learnによるk-means法のコードも紹介し、ライブラリを使うことで非常に効率的なコーディングができるということも体感しました。
教師なし学習と言うと難しそうなイメージでしたが、やってみると案外簡単でしたね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント