Pythonで機械学習をする時の第一歩として線形回帰問題があります。ここでは線形回帰の中でも最も簡単な単回帰分析のPythonプログラミングを通して最初の一歩を踏み出します。
こんにちは。wat(@watlablog)です。機械学習プログラムの実装を学びます!ここでは線形回帰問題の基礎である単回帰分析を紹介します!
回帰問題を解くと未知の事象を予測できる
機械学習における予測
機械学習は主に分類や予測を目的とします。
分類とは、例えばネコの画像を入力した時にコンピュータがネコという解答を出力するといったものです。
一方予測とは、これまで蓄積されたデータから未知の値が入力されたらどういった出力になるかを予め知っておくことです。
データから有用な情報を得たり、この先に起こる現象を予想したりといった事から、マーケティングや工学をはじめとしたあらゆる分野に適用できます。
データから予測するためには、適切なモデルが必要になりますが、このモデルの決定に回帰分析という技術を使います。
回帰とは?
回帰(Regression)とは、変数間の関係を関数で表現することです。
もう少し詳細にいうと、説明変数を使って目的変数を予測する手法です。
当WATLABブログでは、「Pythonでカーブフィット!最小二乗法で直線近似する方法」や「Python多項式カーブフィット!2次以上も最小二乗法を簡単適用」で回帰直線や回帰曲線を紹介しました。
これらの記事ではまさにデータにフィットする関数を選択してパラメータを決めているので、回帰の計算をしていたことになり、この計算を使って分析することを回帰分析と呼びます。
上記2つの記事内では、下のような図を使って最小二乗法の説明を式から説明したり、実際のデータに対してカーブフィットする方法を紹介していますので、ご興味があれば読んでみて下さい。
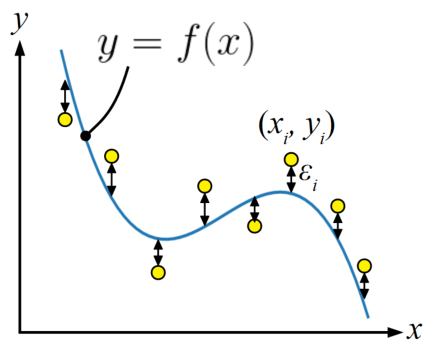
このようにデータから関数(モデル)を構築することができれば、その関数を使って未知の入力に対する出力を補間することができるので、適切なモデルが出来上がれば予測ができるようになると言えます。
実は、都内で有名な占い師は相談者から予測に必要なデータを聞き出し、頭の中で回帰分析をしているという都市伝説が…。信じるか信じないかは(略
numpyを使った回帰分析は前回学びましたが、今後機械学習プログラムを学んでいくにあたってscikit-learnによる回帰分析プログラムも使えるようにしていきましょう。
単回帰分析と重回帰分析
回帰分析を学習すると、単回帰分析と重回帰分析という単語が頻出します。
単回帰分析とは、1つの説明変数から目的変数を予測する分析手法を意味します。 重回帰分析は複数の説明変数を使う所が単回帰分析との違いとなります。
このページではまずは基本のキとして、scikit-learnを使った単回帰分析の方法を紹介します。
scikit-learnによる単回帰分析のコード
scikit-learnについて
本ページではscikit-learnについてはほとんど触れていませんが、「Python機械学習!scikit-kearnインストールと例題」でインストールと動作確認用のコードを紹介していますので、これからscikit-learnをインストールするという方は是非参考にしてみて下さい。
全コード
まずは全コードを以下に載せます。詳細は下の方で解説します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 |
from sklearn import linear_model import numpy as np from matplotlib import pyplot as plt # データを用意する a = 1.0 # 直線の傾き b = 0.5 # y切片 x = np.arange(1.0, 8.0, 0.2) # 横軸を作成 noise = np.random.normal(loc=0, scale=0.5, size=len(x)) # ガウシアンノイズを生成 y = a * x + b + noise # 学習用サンプル波形 # scikit-learnのmodel.fitではデータの次元を明示する必要がある # reshapeを使って各データを1Dデータと明示する x = x.reshape(-1, 1) y = y.reshape(-1, 1) # 線形回帰をする model = linear_model.LinearRegression() # 線形回帰モデルを定義 model.fit(x, y) # 学習実行 reg_y = model.predict(x) # xに対する予測値を計算 # パラメータ算出 reg_a = model.coef_ # 回帰係数 reg_b = model.intercept_ # 回帰定数 r2 = model.score(x, y) # 決定係数 print(reg_a) print(reg_b) print(r2) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸の範囲設定 ax1.set_xticks(np.arange(0, 20, 2)) ax1.set_yticks(np.arange(0, 20, 2)) ax1.set_xlim(0, 10) ax1.set_ylim(0, 10) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.scatter(x, y, label='Dataset') ax1.plot(x, reg_y, label='Regression curve', color='red') plt.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
実行結果
上記コードをエディタにコピペして実行すると、以下のグラフが描画されます。
このプロットは青い点が自作したデータセット、赤い線が学習によって得られた回帰係数、回帰定数でモデル化された関数です。
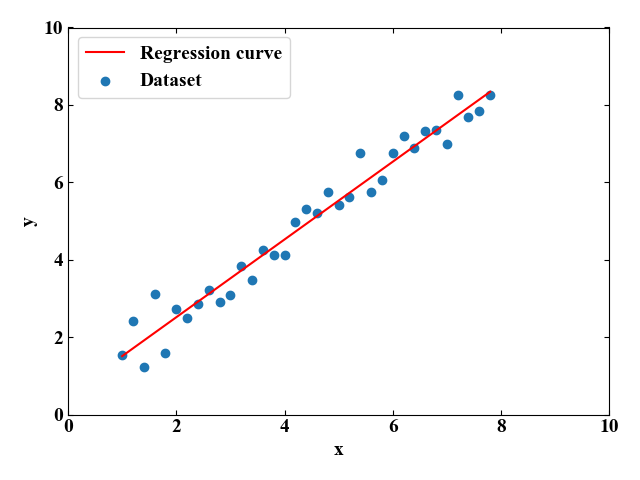
グラフを見ると、よくフィットしているという感覚を持ちますが、回帰係数、回帰定数、決定係数の具体的な数値はコンソールに表示させています。
|
1 2 3 |
[[1.00437887]] # 回帰係数 [0.50588325] # 回帰定数 0.9622867385572451 # 決定係数 |
新出単語が多く出てきましたが、早速プログラムの詳細解説をしていきましょう!
コードの詳細解説
importとデータの用意
importするライブラリパッケージは線形回帰をするためにscikit-learnからlinear_model、データの準備にnumpy、グラフ表示にmatplotlibという3つです。
|
1 2 3 4 5 6 7 8 9 10 |
from sklearn import linear_model import numpy as np from matplotlib import pyplot as plt # データを用意する a = 1.0 # 直線の傾き b = 0.5 # y切片 x = np.arange(1.0, 8.0, 0.2) # 横軸を作成 noise = np.random.normal(loc=0, scale=0.5, size=len(x)) # ガウシアンノイズを生成 y = a * x + b + noise # 学習用サンプル波形 |
データは答えがわかりやすいように直線の式を自作していますが、ガウシアンノイズを含ませる事で実験データっぽく加工しています。
ガウシアンノイズについては当ブログ信号処理カテゴリの「Pythonでガウス分布を持つノイズの作り方と調整方法」という記事に詳細を記載してありますので、こちらもご興味があれば参考にして下さい。
データの次元明示によるエラー回避
以下のコードはデータの次元明示として.reshape処理をしている部分です。.reshapeは1つ目の引数(ここでは-1で変数の長さ)にデータ長、2つ目に次元(ここでは1次元の波形なので1)を指定しているだけなのですが、この処理が無いとエラーになります。
|
1 2 3 4 |
# scikit-learnのmodel.fitではデータの次元を明示する必要がある # reshapeを使って各データを1Dデータと明示する x = x.reshape(-1, 1) y = y.reshape(-1, 1) |
エラーの内容を以下に示します。ここにreshapeをしてくれ、と書いてありますね。
ValueError: Expected 2D array, got 1D array instead:
…
Reshape your data either using array.reshape(-1, 1) if your data has a single feature or array.reshape(1, -1) if it contains a single sample.
reshapeをすると何がどう変わるかは、以下のコードを実行してみるとよくわかります。 このコードは.reshape前後でprint(shape())でshapeを確認しているだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 |
import numpy as np # データを用意する a = 1.0 # 直線の傾き b = 0.5 # y切片 x = np.arange(1, 10, 0.5) # 横軸を作成 noise = np.random.normal(loc=0, scale=1.5, size=len(x)) # ガウシアンノイズを生成 y = a * x + b + noise # 学習用サンプル波形 # shapeを確認 print(np.shape(x)) print(np.shape(y)) # scikit-learnのmodel.fitではデータの次元を明示する必要がある # reshapeを使って各データを1Dデータと明示する x = x.reshape(-1, 1) y = y.reshape(-1, 1) # shapeを確認(reshapeの効果を確認する) print(np.shape(x)) print(np.shape(y)) |
reshape前後でshapeを確認すると、デフォルトでは第2返り値が空欄になっています。scikit-learnの線形回帰ではこの状態では処理が出来ないようです。
そのためデータの内容には変化はないのですが、reshapeで1Dデータであることを明示させてます。
|
1 2 3 4 5 6 7 |
# reshape前 (18,) # x (18,) # y # reshape後 (18, 1) # x (18, 1) # y |
回帰処理
今回のメインは以下の線形回帰コードの部分です。たった3行の内容ですが、ここでデータセットに対する学習を行っています。
まずLinearRegressionとして線形回帰モデルを定義し、.fitで学習を実行、.predictで入力値に対する予測値を計算するという手順です。
|
1 2 3 4 |
# 線形回帰をする model = linear_model.LinearRegression() # 線形回帰モデルを定義 model.fit(x, y) # 学習実行 reg_y = model.predict(x) # xに対する予測値を計算 |
モデル評価
回帰処理まで行えばグラフ描画はできますが、それだけだとモデルのパラメータはどうだったのか、精度はどうかといった評価が出来ません
そこで、以下のコードで学習して出来たモデルの回帰係数と回帰定数を算出しています。
決定係数とは、モデルがどれだけ与えられたデータにフィットしているかを示す指標で、\(R^{2}\)で表します。
|
1 2 3 4 5 6 7 |
# パラメータ算出 reg_a = model.coef_ # 回帰係数 reg_b = model.intercept_ # 回帰定数 r2 = model.score(x, y) # 決定係数 print(reg_a) print(reg_b) print(r2) |
回帰係数とは、今回は直線で表現できるモデルなので直線の傾きに相当します。
回帰定数は同様に今回はy切片を意味します。
全コードを実行すると以下の結果が得られますが、回帰係数と回帰定数はデータ用意の時点で決めたaとbの値に近い数値となっています。決定係数も0.96と高い値(最大が1)を示しているので、今回のモデルは精度が良いと言えそうです。
|
1 2 3 |
[[1.00437887]] # 回帰係数 [0.50588325] # 回帰定数 0.9622867385572451 # 決定係数 |
ガウシアンノイズの標準偏差を大きい値にしたりいじわるをすればこれらの値はどんどん悪くなることでしょう。
この辺は重回帰分析の時に詳しく説明しようと思います(できれば…)。
まとめ
本記事ではまず始めに、機械学習における予測と回帰分析の概要を説明しました。
また、scikit-learnの単回帰分析の例をコードを用いて紹介しました。
この単回帰分析が機械学習の基礎の基礎となっていると考えられるので、まずはこの内容をしっかりと理解することが重要です。
基礎とはいえ、実際にコーディングしていくと理解はさらに深まります!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント