
技術計算の分野では、測定されたデータを任意の関数にカーブフィットする需要が頻繁にあります。Pythonのscipy.optimize.curve_fitを使えば点列データを1次元や2次元の関数で簡単にフィッティングできます。ここでは様々な関数を例にcurve_fitを使ってみた内容を紹介します。
こんにちは。wat(@watlablog)です。本日は超便利な関数近似メソッドであるscipy.optimize.curve_fitを使ってみた結果を紹介します!
本記事の目標
1Dと2Dデータに対するcurve_fitの使い方を理解する
線形近似から学ぶ
関数近似入門としての代表例は最小二乗法による線形近似です。線形近似については以下の記事で数式展開もしながら解説していますが、直線の方程式でデータを近似するだけでも多くの分析が可能なデータ分析の王道手法です。
まずはこの内容をscipy.optimize.curve_fitでできるようにして、基礎を理解しましょう。
・Pythonでカーブフィット!最小二乗法で直線近似する方法
様々な関数で応用力を付ける
線形近似の次は多項式近似に進み、その後は指数関数や対数関数による近似をしてみます。この辺りでExcelのグラフ上で行う関数近似は網羅できるのですが、この記事ではさらに三角関数や確率密度分布がそれぞれ近似できるような内容も載せました。
scipy.optimize.curve_fitは任意関数として設定する方程式を変えるだけでこれらの近似ができるので、ここまでくれば1Dのどんなデータが来ても対応できるでしょう。
曲面フィッティングもやってみる
説明変数が2つの重回帰分析をはじめとする曲面で近似したい場面も多くあります。ここでは2Dのデータに対して自分で設定した曲面を表現する関数にどうフィッティングさせるか、その結果の可視化方法も併せて紹介します。
直接的な可視化限界である2変数問題が扱えるようになれば、あとは超平面へのカーブフィットもコーディングできるようになるはずです(ここでは扱いませんが、可視化は結局写像して3Dプロットとかかな?)。
色々やりますが、結局は公式で紹介されていることをベースにしているだけです。公式ドキュメントはこちら↓。いつでも1次情報を確認するようにしましょう。
・https://docs.scipy.org/doc/scipy/reference/generated/scipy.optimize.curve_fit.html
動作環境
本記事のコードは以下の環境で動作を確認しました。
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.23.0 |
| Scipy | 1.4.1 |
| matplotlib | 3.7.1 |
1Dデータの関数近似例
多項式近似
線形近似(初回詳細解説):\(ax+b\)
直線の方程式(1)を使ってコードの基礎を確認します。
線形近似(線形回帰)を行うコードは段階を追ってコードを見ていきましょう。
まずはimport文を書きます。SciPyは膨大なパッケージですので、from scipy.optimize import curve_fitと必要なモジュールだけ取り込みます。
|
1 2 3 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt |
任意関数として直線の方程式を関数の形で記載します。第1引数xが変数で、その後に式に使う係数を続けます。return文に計算後の結果を渡すという至極一般的な関数の書き方です。
|
1 2 3 4 5 6 |
def func(x, a, b): """ 式 """ y = a * x + b return y |
テストするためのデータセット(点列データ)を準備しましょう。以下のコードは先ほど作った関数funcに引数を渡してデータを作っているものです。ただ、それだけだと方程式通りの綺麗なデータになってしまい面白くないので、np.random.normalでガウス分布を持つノイズを混入させています。
|
1 2 3 4 |
# データセットを生成 n = 10 x = np.arange(0, 1, 0.1) y = func(x, 1, 0) + np.random.normal(loc=0, scale=0.2, size=len(x)) |
ランダム成分があるので毎回完全一致はしませんが、下図の結果が得られるはずです(可視化の方法は後述します)。
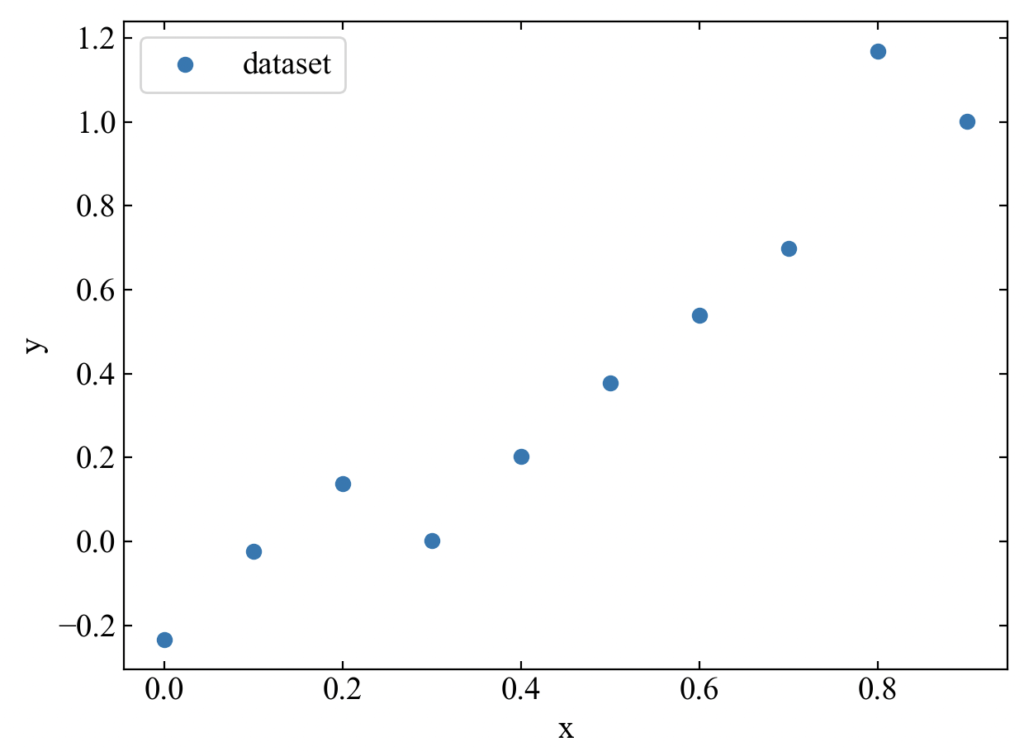
そしていよいよカーブフィットを行います。カーブフィットはcurve_fit()に近似に使う関数funcそのものとデータセットx, yを与えるだけです。
|
1 2 |
# カーブフィット popt, pcov = curve_fit(func, x, y) |
結果がpoptとpcovの2つあります。poptは最適化されたパラメータ(\(p_{opt}\))、pcovはパラメータの分散共分散行列(共分散=covariance)です。
pcovの対角成分を使えば以下の文でパラメータ毎に誤差を調べることができます。
|
1 |
print('error=', np.sqrt(np.diag(pcov))) |
この誤差errorの値が大きいほど、データによくフィットできていないということがわかります。
|
1 |
error= [0.15286971 0.08161009] |
最後に最適化されたパラメータを使って近似された関数の形を確認します。poptは任意に設定した関数の引数の数に応じてサイズが変わりますが、*poptとアスタリスクを付けて書くことで一度に複数の引数を設定できます。つまり、関数によってこの部分の書き方を変えなくても良いというメリットがあります。
|
1 2 |
x_pred = np.linspace(np.min(x), np.max(x), 1000) y_pred = func(x_pred, *popt) |
こちらがデータと近似結果を比較したプロットです。イメージ通りですね。
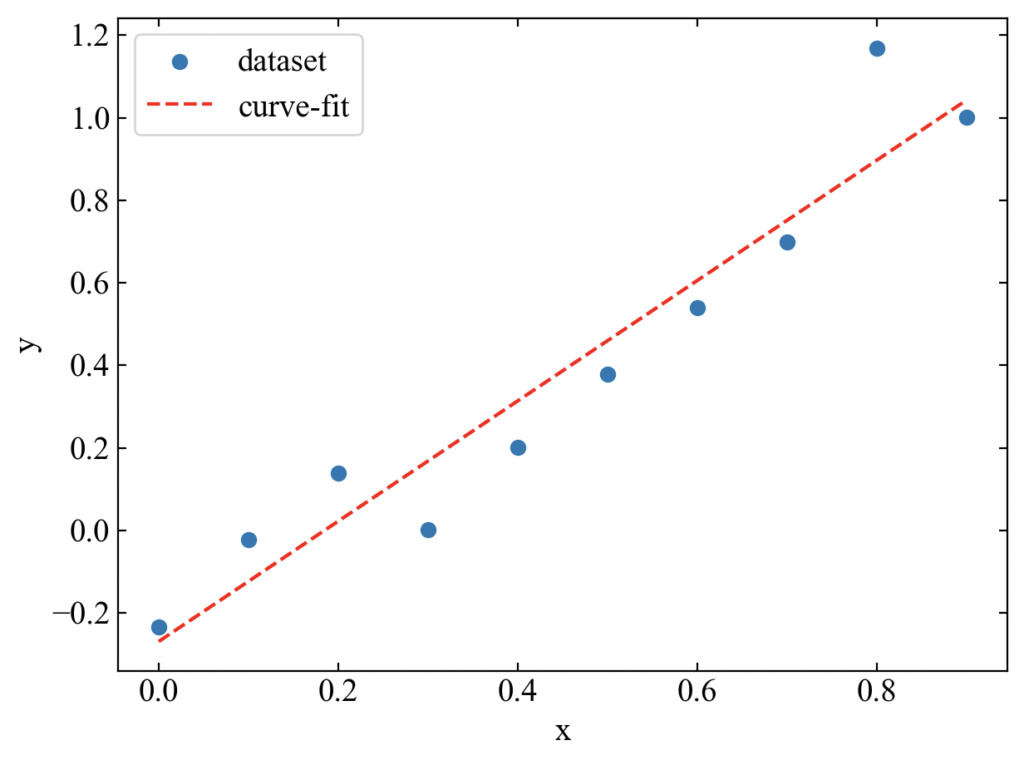
matplotlibによる可視化方法も含めた全コードを以下に示します。コピペで動作するはずなので是非ご自分の環境で動かしてみてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(x, a, b): """ 式 """ y = a * x + b return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 x = np.arange(0, 1, 0.1) y = func(x, 1, 0) + np.random.normal(loc=0, scale=0.2, size=len(x)) # グラフ描画 plot([x], [y], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, x, y) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(x), np.max(x), 1000) y_pred = func(x_pred, *popt) plot([x, x_pred], [y, y_pred], ['dataset', 'curve-fit']) |
\(ax^2+bx+c\)
基本的な使い方がわかったので、式を変更してどんどんカーブフィットを試してみましょう。次は2次方程式(2)を近似します。
コードは式とデータセット生成部分を変更するだけですが、どこから読みはじめてもコピペで動作できるように毎回全コードを載せます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(x, a, b, c): """ 式 """ y = a * x ** 2 + b * x + c return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 x = np.arange(-5, 5, 0.5) y = func(x, 1, 1, 1) + np.random.normal(loc=0, scale=1.0, size=len(x)) # グラフ描画 plot([x], [y], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, x, y) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(x), np.max(x), 1000) plot([x, x_pred], [y, func(x_pred, *popt)], ['dataset', 'curve-fit']) |
良い近似結果です!
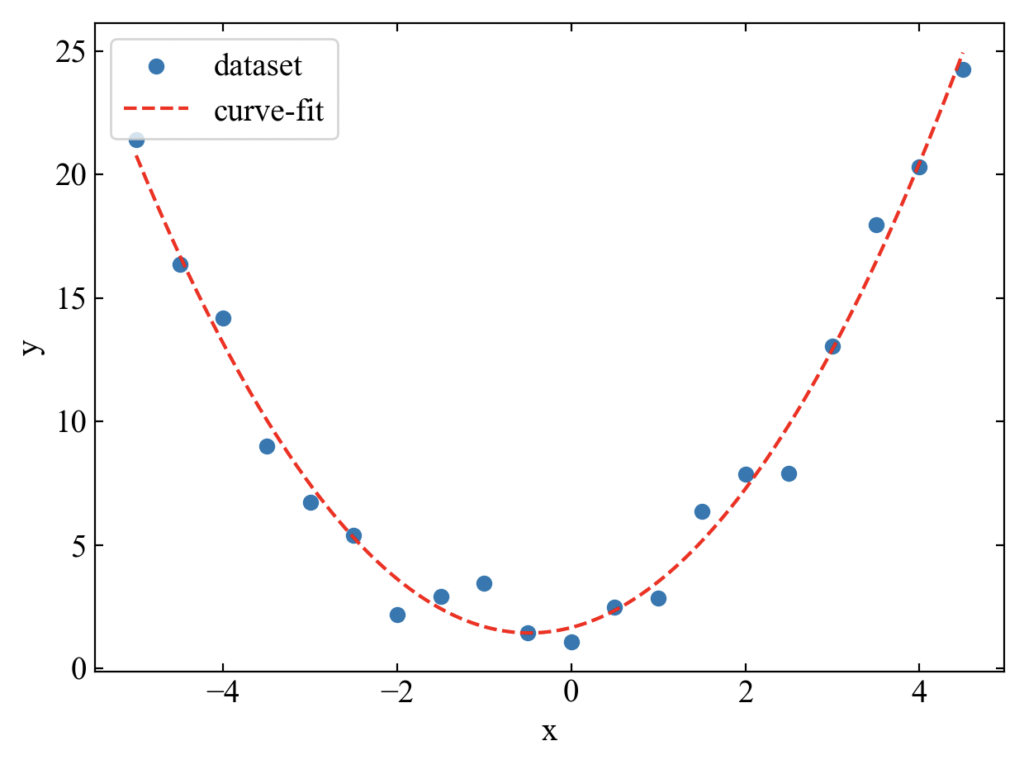
\(ax^3+bx^2+cx+d\)
続いて3次方程式(3)です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(x, a, b, c, d): """ 式 """ y = a * x ** 3 + b * x ** 2 + c * x + d return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 x = np.arange(-5, 5, 0.5) y = func(x, 1, 1, 1, 1) + np.random.normal(loc=0, scale=5.0, size=len(x)) # グラフ描画 plot([x], [y], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, x, y) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(x), np.max(x), 1000) y_pred = func(x_pred, *popt) plot([x, x_pred], [y, y_pred], ['dataset', 'curve-fit']) |
良い近似…(以下略)
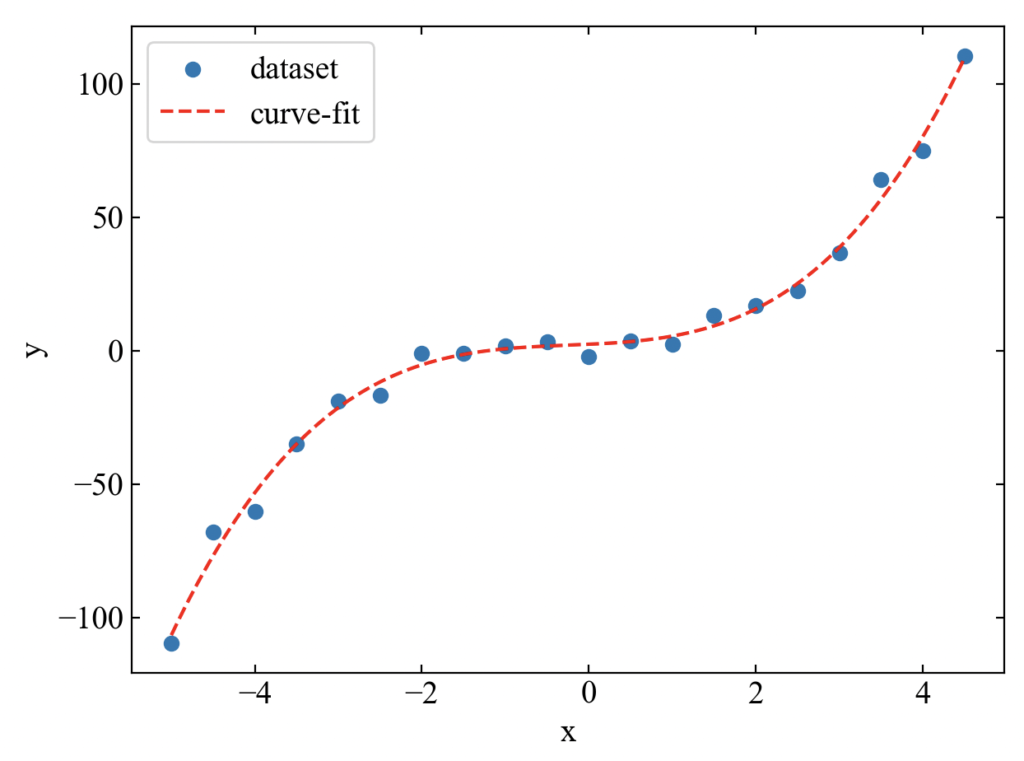
指数関数近似/対数関数近似
\(e^{x}\)
続いて指数関数(4)の近似をしてみます。式全体に係数をつけていますが、xにも何かかけても良いかも知れません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(x, a): """ 式 """ y = a * np.exp(x) return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 x = np.arange(-1, 5, 0.2) y = func(x, 1) + np.random.normal(loc=0, scale=5, size=len(x)) # グラフ描画 plot([x], [y], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, x, y) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(x), np.max(x), 1000) y_pred = func(x_pred, *popt) plot([x, x_pred], [y, y_pred], ['dataset', 'curve-fit']) |
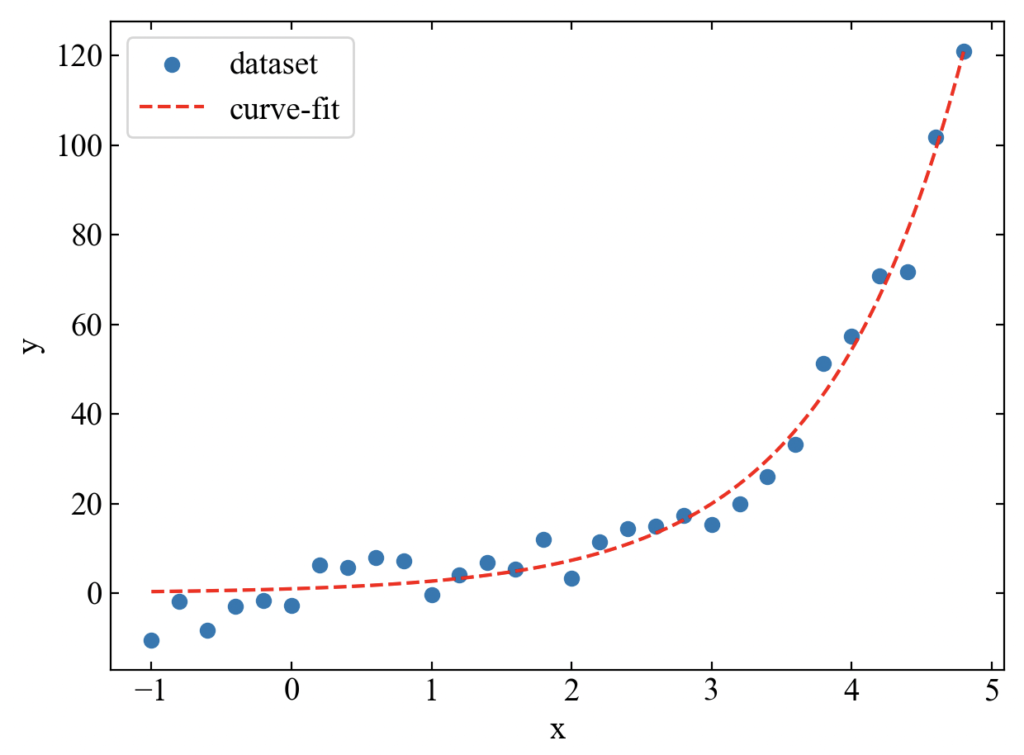
\(\log{x}\)
続いて対数関数(5)を近似します。
対数関数はxの範囲に0をとってしまうとエラーになるので、その部分もちょっと変更しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(x, a): """ 式 """ y = a * np.log(x) return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 x = np.arange(0.1, 5, 0.2) y = func(x, 1) + np.random.normal(loc=0, scale=0.2, size=len(x)) # グラフ描画 plot([x], [y], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, x, y) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(x), np.max(x), 1000) y_pred = func(x_pred, *popt) plot([x, x_pred], [y, y_pred], ['dataset', 'curve-fit']) |
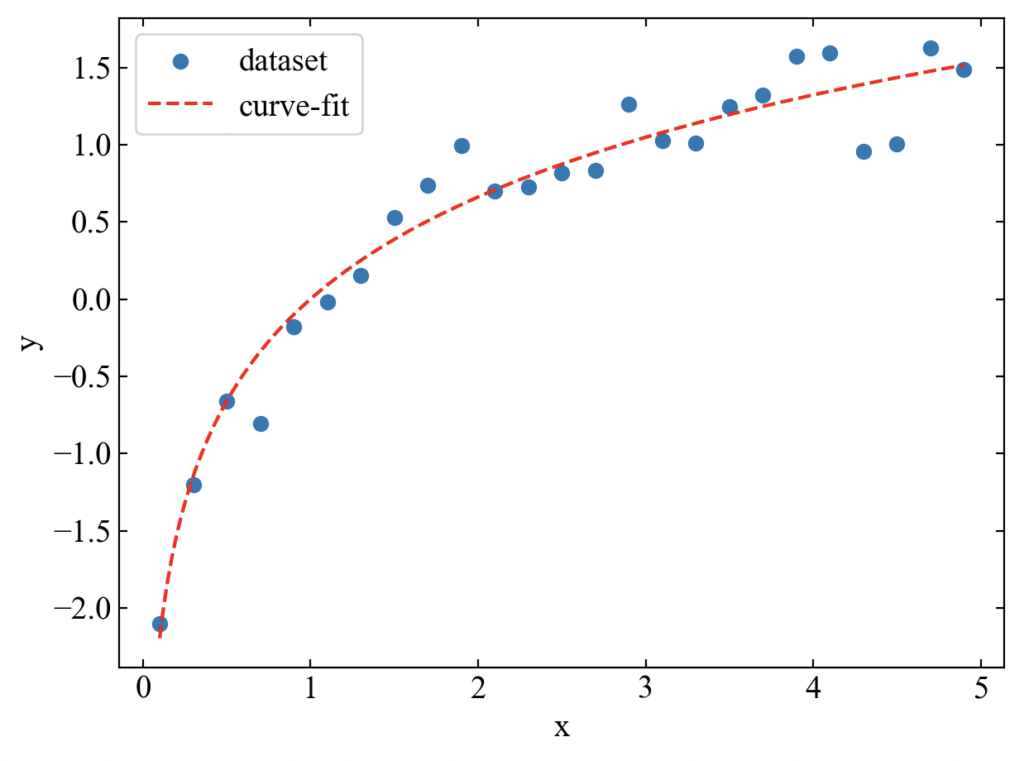
三角関数近似
\(\sin x\)
簡単過ぎてもはや単なる作業になってきましたが、近似したい関数の中でも人気(?)なサインカーブ(6)も近似してみましょう。波の特性がわかりやすくなるように、xを時間と仮定して周波数fの概念を入れてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(x, a, f): """ 式 """ y = a * np.sin(2 * np.pi * f * x) return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 a = 1 # 振幅 f = 1 # 周波数[Hz] x = np.arange(-1, 1, 0.1) y = func(x, 1, f) + np.random.normal(loc=0, scale=0.1, size=len(x)) # グラフ描画 plot([x], [y], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, x, y) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(x), np.max(x), 1000) y_pred = func(x_pred, *popt) plot([x, x_pred], [y, y_pred], ['dataset', 'curve-fit']) |
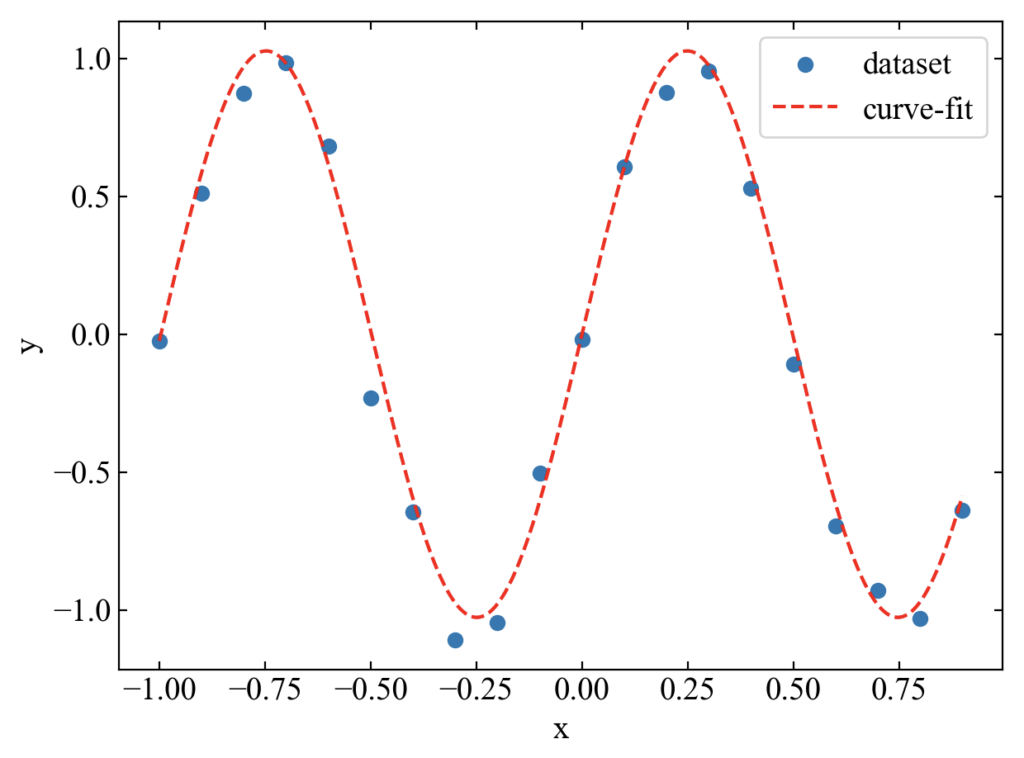
\(\cos x\)
サインをやっておいてコサインが無いのも気持ちが悪いので、コサインカーブ(7)も載せておきます。ただこちらは上記func()関数内sin部分をcosにするだけなのでコードは割愛し、結果だけお見せします。
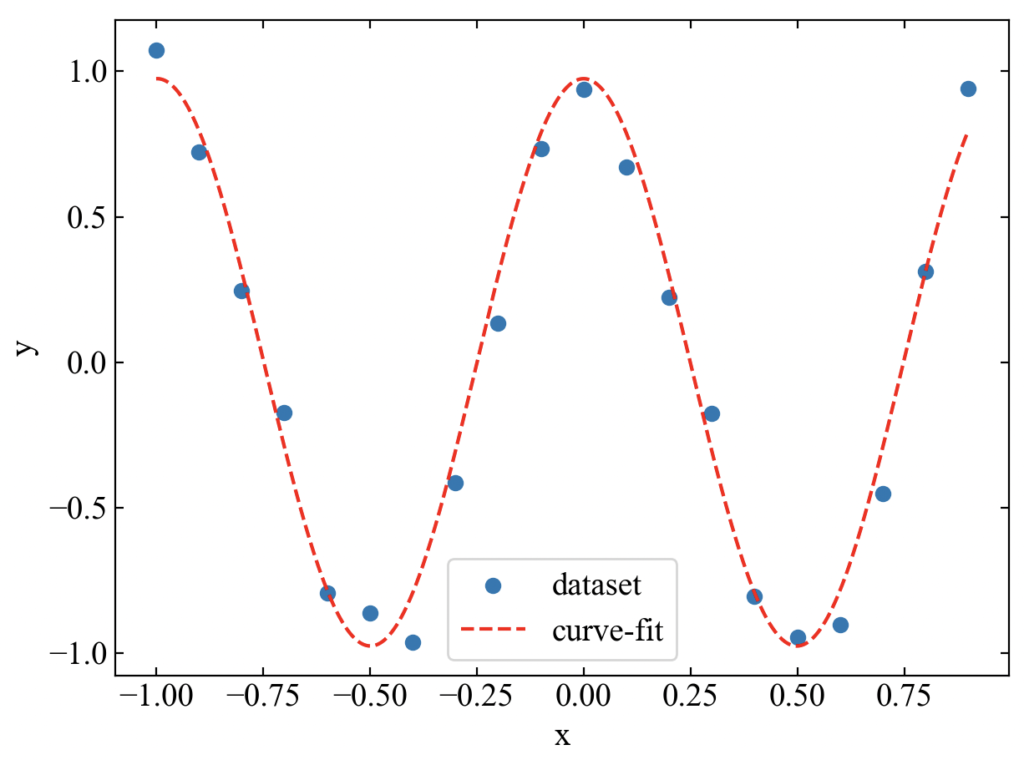
\(\tan x\)
三角関数シリーズでタンジェントだけ仲間はずれにするのは可哀想ということで、タンジェントカーブ(8)も近似しましょう。
\(\tan\)はy軸が大きくなりすぎるので、matplotlibにスケール設定を追加してみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(x, a, f): """ 式 """ y = a * np.tan(2 * np.pi * f * x) return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケール設定 ax1.set_ylim(np.min(y[0]), np.max(y[0])) # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 a = 1 # 振幅 f = 1 # 周波数[Hz] x = np.arange(-1, 1, 0.1) y = func(x, 1, f) + np.random.normal(loc=0, scale=0.1, size=len(x)) # グラフ描画 plot([x], [y], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, x, y) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(x), np.max(x), 1000) y_pred = func(x_pred, *popt) plot([x, x_pred], [y, y_pred], ['dataset', 'curve-fit']) |
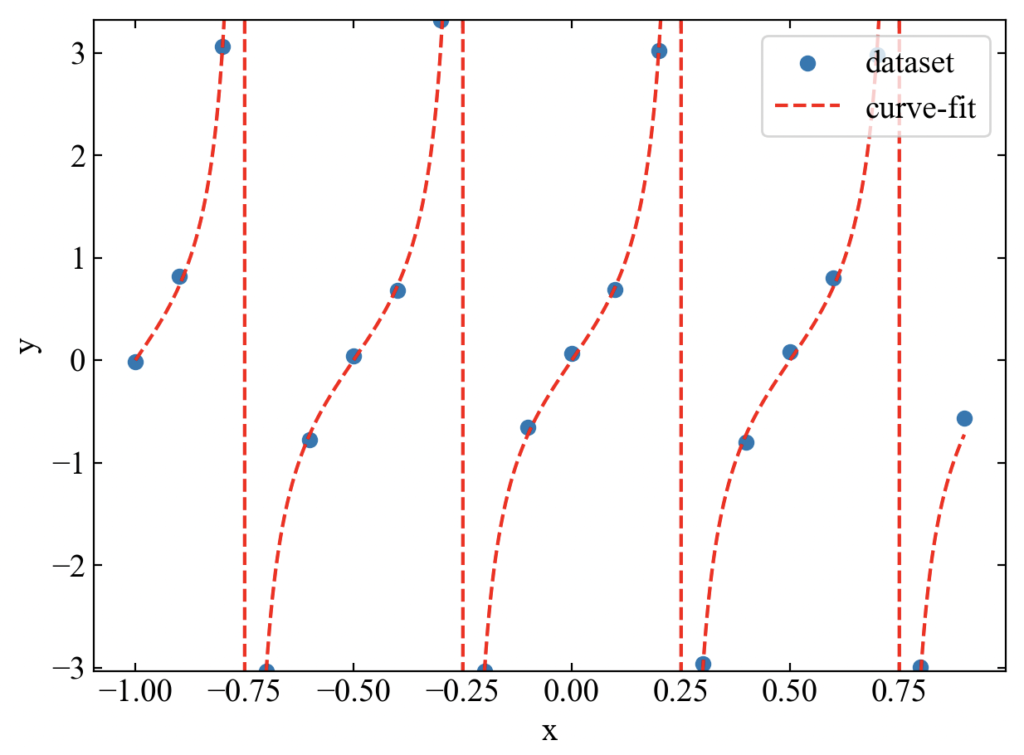
他にも三角関数や指数関数の親戚である双曲線関数(\(\sinh\)とか)も関数func部分を変更するだけで試すことができます。ここでは割愛しますが、是非お好みの関数で近似してみてください。
1次元確率密度関数近似
実験データを多数取得した時、データを任意の値域(ビン)でカウントしたヒストグラムを描くことが多いです。ヒストグラムに対して平均や標準偏差を調べることは統計的に実験データを解釈するのに必要なので、確率密度関数でデータを近似するのは非常に重要なことです。
式(9)はガウス分布を持つ確率密度関数です。代表的な例として、この式で近似するコードを紹介します。
このコードは先ほどまでと異なり、ヒストグラムを作成する関数から書いています。その後、その作成されたデータを用いてカーブフィットをするという流れです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def data_gaussian_1d(n, mu, sigma): """ 1次元ガウシアンノイズのデータ点とヒストグラムを計算する関数(サンプルデータ生成) """ # データ点を生成しヒストグラムを作成する p = np.random.normal(loc=mu, scale=sigma, size=n) count, boundary = np.histogram(p, bins=10) # プロット用にboundary配列を隣り合う要素の中心配列とする val = [] for i in range(len(boundary) - 1): val.append((boundary[i] + boundary[i+1]) / 2) return val, count def func_gaussian(x, a, mu, sigma): """ ガウス関数 """ y = a * np.exp(-(x - mu) ** 2 / (2 * sigma ** 2)) return y def plot(x, y, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Bins') ax1.set_ylabel('Count') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter(x[i], y[i], label=label[i]) else: ax1.plot(x[i], y[i], label=label[i], c='red', linestyle='dashed') ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # ガウス分布を持つデータセットを生成 n = 1000 mu = 0 sigma = 1 val, count = data_gaussian_1d(n, mu, sigma) # グラフ描画 plot([val], [count], ['dataset']) # カーブフィット popt, pcov = curve_fit(func_gaussian, val, count) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 x_pred = np.linspace(np.min(val), np.max(val), 1000) y_pred = func_gaussian(x_pred, *popt) plot([val, x_pred], [count, y_pred], ['dataset', 'curve-fit']) |
こちらが近似結果です。綺麗に近似できていますね!poptを見れば平均や標準偏差の値を調べることができます(パラメータとして設定してあるので)。
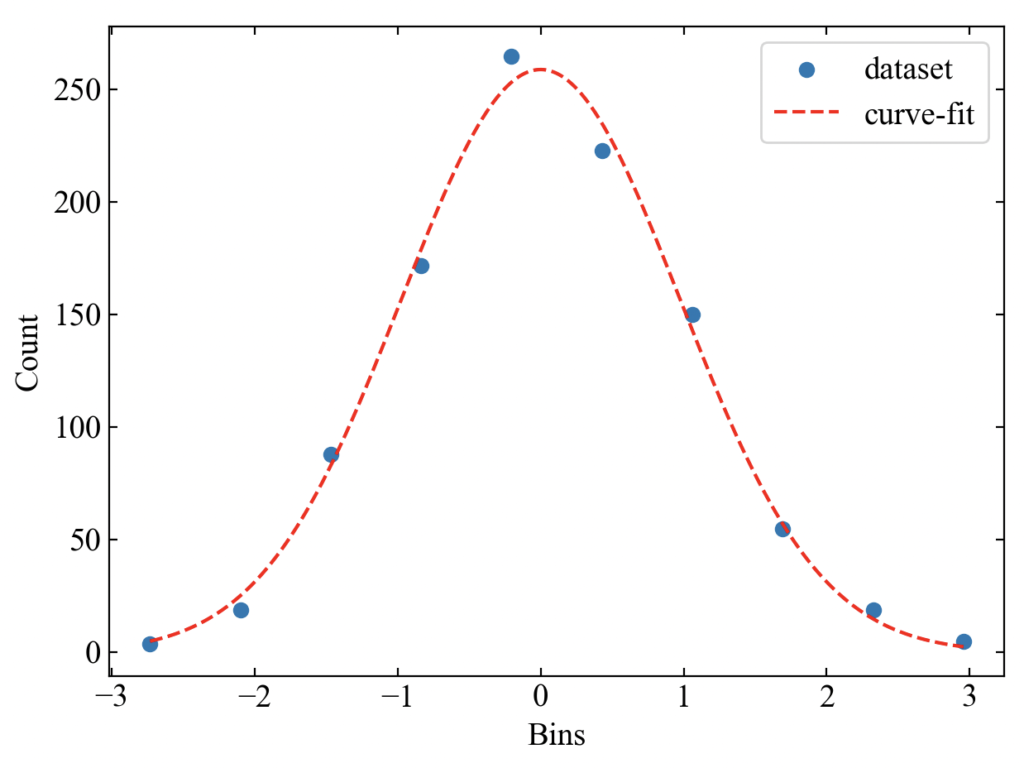
2Dデータの関数近似例
次は1次元ではなく、2次元のデータに対して近似を行う方法を試してみましょう。
2次元確率密度関数近似
先ほどの続きで確率密度関数の2次元版をやってみます。近似する式は式(10)です。
こちらがコードです。2次元の場合は可視化するためにnp.meshgridを使っていたり、ややデータ整形にややこしいことがあります。地味にnp.histogram2d等も使っていますが、これは理想のデータを生成するためのコードなので、実際は実験データ等をそのまま使うことが可能です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def data_gaussian_2d(n, mu, sigma): """ 2次元ガウシアンノイズのデータ点とヒストグラムを計算する関数(サンプルデータ生成) """ p = np.random.multivariate_normal(mu, sigma, n) count, boundary1, boundary2 = np.histogram2d(p.T[0], p.T[1], bins=[10, 10]) # プロット用にboundary配列を隣り合う要素の中心配列とする val1 = [] val2 = [] for i in range(len(boundary1) - 1): val1.append((boundary1[i] + boundary1[i + 1]) / 2) val2.append((boundary2[i] + boundary2[i + 1]) / 2) X, Y = np.meshgrid(val1, val2) return X, Y, count def func_gaussian(X, a, mu_x, mu_y, sigma_x, sigma_y): """ 2次元ガウス関数 """ x, y = X z = a * np.exp(-(x - mu_x) ** 2 / (2 * sigma_x ** 2)) * np.exp(-(y - mu_y) ** 2 / (2 * sigma_y **2)) return z.ravel() def plot(x, y, z, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Bins x') ax1.set_ylabel('Bins y') ax1.set_zlabel('Count') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter3D(x[i], y[i], z[i], s=10, label=label[i], c='yellow', edgecolor='black') else: ax1.plot_surface(x[i], y[i], z[i], label=label[i], alpha=0.5, cmap='jet') # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # ガウス分布を持つデータセットを生成 n = 1000 mu = [0, 0] sigma = [[10, 0], [0, 10]] val1, val2, count = data_gaussian_2d(n, mu, sigma) # グラフ描画 plot([val1], [val2], [count], ['dataset']) # カーブフィット X = np.array([val1, val2]) popt, pcov = curve_fit(func_gaussian, X, count.ravel()) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 n_pred = 50 axis_x = np.linspace(np.min(val1), np.max(val1), n_pred) axis_y = np.linspace(np.min(val2), np.max(val2), n_pred) X_pred, Y_pred = np.meshgrid(axis_x, axis_y) Z_pred = func_gaussian(np.array([X_pred, Y_pred]), *popt) Z_pred = np.reshape(Z_pred, (n_pred, -1)) plot([val1, X_pred], [val2, Y_pred], [count, Z_pred], ['dataset', 'curve-fit']) |
こちらが結果です。うーん、いいですね!
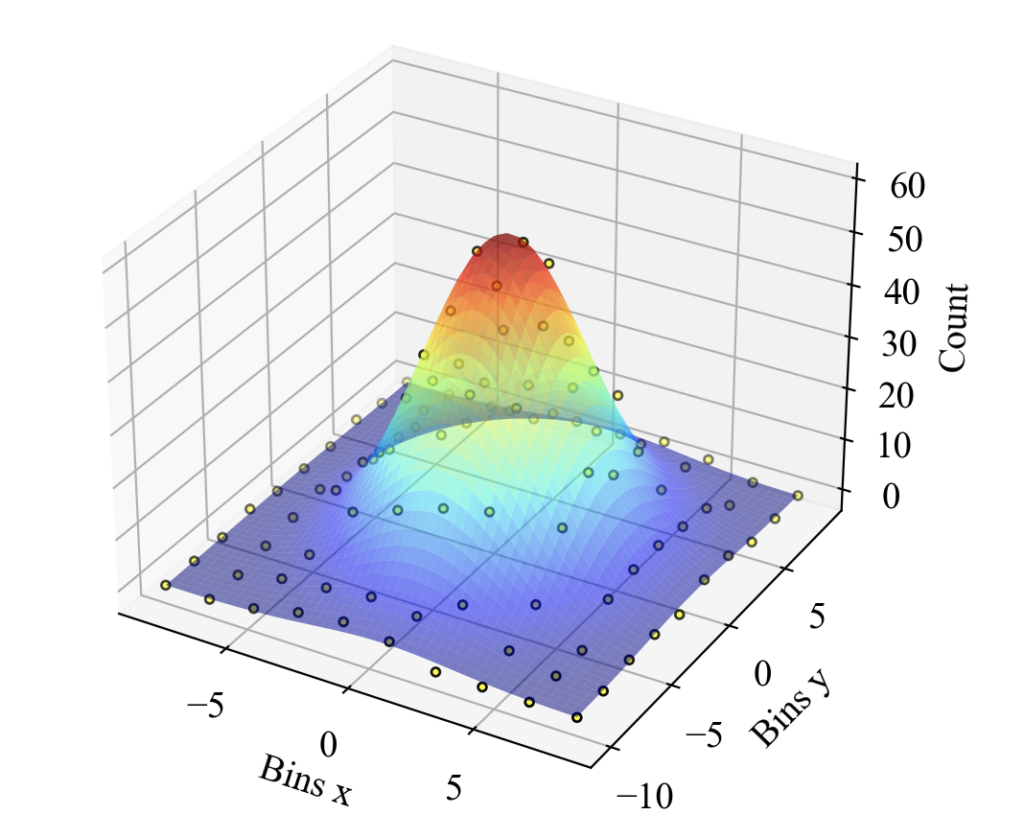
2D平面近似:\(z = w_{0} + w_{1} x + w_{2}y\)
次は重回帰分析でよくお世話になる2次元平面の式(11)です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(X, w0, w1, w2): """ 2次元平面の式 """ x, y = X z = w0 + w1 * x + w2 * y return z.ravel() def plot(x, y, z, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter3D(x[i], y[i], z[i], s=10, label=label[i], c='yellow', edgecolor='black') else: ax1.plot_surface(x[i], y[i], z[i], label=label[i], alpha=0.5, cmap='jet') # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 10 x = np.linspace(-10, 10, n) y = np.linspace(-10, 10, n) X, Y = np.meshgrid(x, y) w0 = 0 w1 = 1 w2 = 2 P = np.array([X, Y]) Z = func(P, w0, w1, w2) noise = np.random.normal(loc=0, scale=5, size=len(Z)) Z = Z + noise # グラフ描画 plot([X], [Y], [Z], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, P, Z) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 n_pred = 50 axis_x = np.linspace(np.min(X), np.max(X), n_pred) axis_y = np.linspace(np.min(Y), np.max(Y), n_pred) X_pred, Y_pred = np.meshgrid(axis_x, axis_y) P_pred = np.array([X_pred, Y_pred]) Z_pred = func(P_pred, *popt) Z_pred = np.reshape(Z_pred, (n_pred, -1)) plot([X, X_pred], [Y, Y_pred], [Z, Z_pred], ['dataset', 'curve-fit']) |
こちらも綺麗にフィッティングできています!
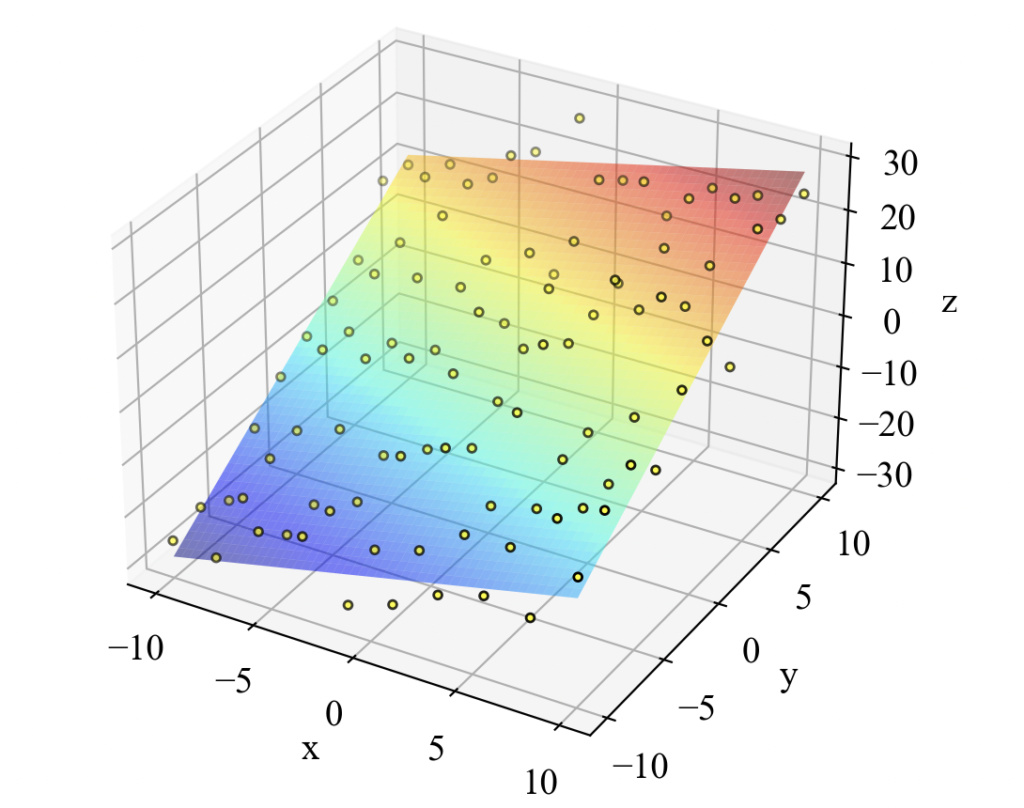
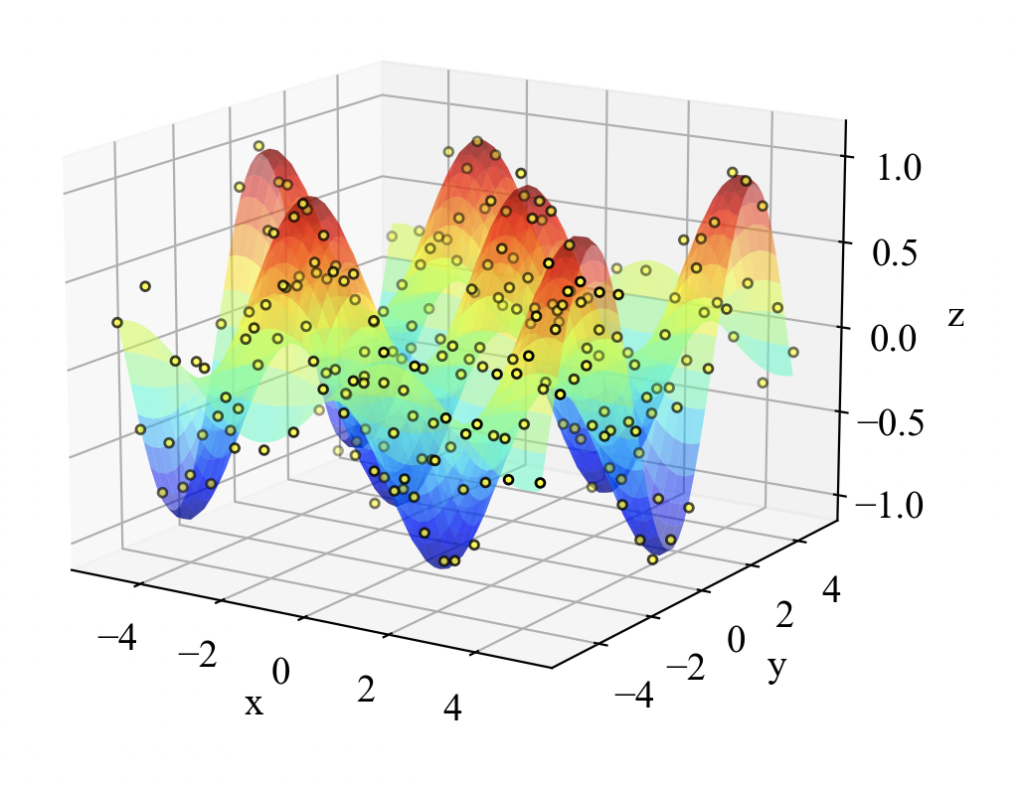
\(z = \sin (x) \cos(y)\)
2Dデータに対するフィッティングがわかってきたので、最後はお気に入りの式(12)を近似してみます。
コードはこちら。一度できたら小変更で済むのがプログラミングのすごいところですね。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
import numpy as np from scipy.optimize import curve_fit from matplotlib import pyplot as plt def func(X, a, b): """ 2次元sin*cosの式 """ x, y = X z = a * np.sin(x) * b * np.cos(y) return z.ravel() def plot(x, y, z, label): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') # データをプロットする。 for i in range(len(x)): if i == 0: ax1.scatter3D(x[i], y[i], z[i], s=10, label=label[i], c='yellow', edgecolor='black') else: ax1.plot_surface(x[i], y[i], z[i], label=label[i], alpha=0.5, cmap='jet') # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # データセットを生成 n = 15 x = np.linspace(-5, 5, n) y = np.linspace(-5, 5, n) X, Y = np.meshgrid(x, y) a = 1 b = 1 P = np.array([X, Y]) Z = func(P, a, b) noise = np.random.normal(loc=0, scale=0.1, size=len(Z)) Z = Z + noise # グラフ描画 plot([X], [Y], [Z], ['dataset']) # カーブフィット popt, pcov = curve_fit(func, P, Z) print('optimized parameters=', popt) print('variance-covariance matrix=', pcov) print('error=', np.sqrt(np.diag(pcov))) # グラフ描画 n_pred = 50 axis_x = np.linspace(np.min(X), np.max(X), n_pred) axis_y = np.linspace(np.min(Y), np.max(Y), n_pred) X_pred, Y_pred = np.meshgrid(axis_x, axis_y) P_pred = np.array([X_pred, Y_pred]) Z_pred = func(P_pred, *popt) Z_pred = np.reshape(Z_pred, (n_pred, -1)) plot([X, X_pred], [Y, Y_pred], [Z, Z_pred], ['dataset', 'curve-fit']) |
まとめ
本日はここまで!
この記事ではscipy.optimize.curve_fitによる関数近似の事例をまとめました。1次元だけではなく、2次元の点列データに対するカーブフィッティングも簡単に行うことができました。
これは久しぶりに汎用性の高いメソッドを見つけたと思うので、実際のデータ分析業務で活用ができそうです。
任意関数のカーブフィットはもはやこれで十分なのでは??
X(旧Twitter)でも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!