回転機の振動シミュレーションで回転パルスを設定してみた

先日の記事で回転機のアンバランス振動シミュレーションをPythonで行いました。振れ回り振動と参考書の対応がとれたので、次はより詳細な分析を行うために回転パルス（基準信号）をシミュレーションで設定してみます。ここではPythonのodeintで基準パルスを設定しながらアンバランス振動のシミュレーションを行う方法を紹介します。

こんにちは。wat(@watlablog)です。回転機のシミュレーションを進めていくために、この記事では回転パルスをシミュレーションで表現する方法を紹介します！

目次（項目クリックでジャンプできます）

回転パルスをシミュレーションで再現する理由

回転機シミュレーションのおさらい

以下の記事では回転機のシミュレーションをしてみました。この記事の中ではアンバランス振動の運動方程式を導出し、Pythonのodeintを使って振れ回り振動が出ることを確認しています。
・回転機のアンバランス振動をシミュレートするPythonコード

バランス修正には回転パルスの計測が重要

回転機を扱う実際の現場では、アンバランス振動を計測してバランスの悪さを修正する工程が存在します。タイヤ、モータのアーマチュア、換気扇のファン…と世の中には多数のバランス調整を必要とする機械があります。

もしかしてあなたの家のエアコン室外機用ファンも、バランス調整をした後の形跡（ブレードがもっこりしている、クリップがついている…等）があるのでは？

実際はアンバランスを加速度センサーやひずみゲージ、力センサーで振動を計測します。
しかし、これらのセンサーを単体で使っている場合、振動の大小はわかってもどこに修正錘を取り付ければ良いかがわかりません。

回転パルスを振動と同期計測することで、回転機の機械角と振動の位相差\(\phi\)を知ることが可能です。

下図は回転機に反射テープを貼り、レーザーで回転パルス、振動センサーで振動を計測している例です。通常回転パルスは一回転に一回の電圧降下（または電圧上昇）を発生させることで位置検出を行います。

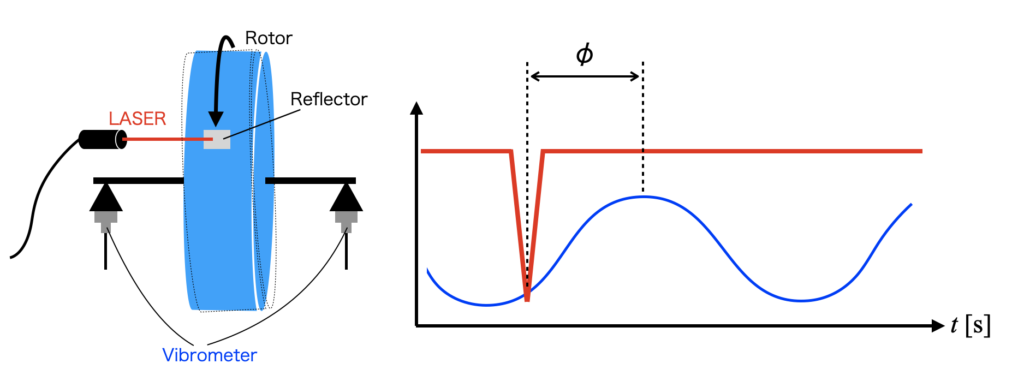
振動のピークとアンバランスのある場所を知ることでバランスの修正ができるため、回転位置検出が精密な回転を実現させるキーポイントとなります。

共振が発生すると位相がずれる

回転機の位置検出原理は非常に理解しやすいですが、世の中の回転機が弾性体であることがやや検出を難しくします。

参考文献\(^{[1]}\)によると、アンバランス偏心と振動の位相関係は共振に左右されるとあります。一般的な1自由度ばねマス系でも共振で位相が変わるのはよく知られていますが、位置検出が重要な回転機ではその特徴が計測の最大の問題点となる場合があるでしょう。

そのため共振問題に頻繁にさらされる回転機のシミュレーションをできるようにすることは非常に重要です。

この記事ではまず1つだけ共振を持つ回転機のシミュレーションをしてみます。複数の共振を持つ回転機はおそらく以下の記事にあるような多自由度振動系のシミュレーション手法が使えると思うので、このページでは基礎的なことのみ扱います。
・Pythonで多自由度振動系の過渡応答計算をする時はSciPyを使おう

SciPyのodeintで回転パルスを追加するPythonコード

動作環境

この記事のコードは以下のPython環境で動作確認をしています。後半に動画を作成するコードを紹介している都合でpillowも使っています。

■Python環境

Python	Python 3.9.6
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.21.1
Scipy	1.4.1
matplotlib	3.4.3
pillow	7.1.2

全コード

以下に「回転機のアンバランス振動をシミュレートするPythonコード」で紹介したシミュレーションへ回転パルス生成処理を追加したコードを示します。

回転パルスは\(\cos \omega t\)を基準として関数fの中で計算しています。odeintに渡す積分するための関数なので式（1）の微分形式にしています。

\[ \left\{\begin{matrix} p &=& \cos \omega t \\ \dot{p} &=& - \omega \sin \omega t \\ \ddot{p} &=& - \omega^{2} \cos \omega t \\ \end{matrix}\right. \tag{1} \]

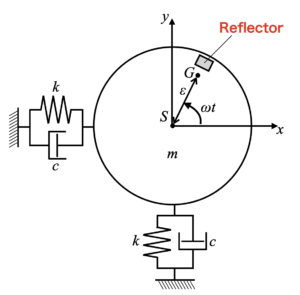
今回のシミュレーションは偏心位置に反射テープを貼っていることを想定します。力学モデル上で図示すると以下になります。

import numpy as np
from matplotlib import pyplot as plt
from scipy.integrate import odeint


def f(var, t, m, k, c, epsilon, omega):
    ''' 運動方程式：回転機のアンバランス振動 '''

    # xとy、変位と速度に分ける
    x = var[0]
    y = var[1]
    x_dot = var[2]
    y_dot = var[3]

    # 回転パルスの変数を抽出
    pulse = var[4]
    pulse_dot = var[5]

    # 運動方程式
    x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x
    y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

    # 回転パルスの2階微分
    pulse_ddot = - omega ** 2 * np.cos(omega * t)

    # 結果
    output = [x_dot, y_dot, x_ddot, y_ddot, pulse_dot, pulse_ddot]

    return output


def plot(t, x, y, pulse, N):
    ''' Plot '''

    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure(figsize=(10, 5))
    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')
    ax2 = ax1.twinx()

    # 軸のラベルを設定する。
    ax1.set_xlabel('t[s]')
    ax1.set_ylabel('Displacement[m]')
    ax2.set_xlabel('t[s]')
    ax2.set_ylabel('Pulse[V]')

    # 回転数から周期を計算（データ抽出用）
    freq = N / 60
    cycle = 1 / freq
    dt = t[1]
    sample_cycle = int(cycle / dt)
    size = len(t)

    # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
    ax1.plot(t[size - 2 * sample_cycle::], x[size - 2 * sample_cycle::], label='x', lw=3, color='red')
    ax1.plot(t[size - 2 * sample_cycle::], y[size - 2 * sample_cycle::], label='y', lw=3, color='blue')
    ax2.plot(t[size - 2 * sample_cycle::], pulse[size - 2 * sample_cycle::], label='pulse', lw=1, color='black')

    # 凡例をまとめて出力する
    handler1, label1 = ax1.get_legend_handles_labels()
    handler2, label2 = ax2.get_legend_handles_labels()
    ax1.legend(handler1 + handler2, label1 + label2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

    # レイアウト設定
    fig.tight_layout()

    # グラフを表示する。
    plt.show()
    plt.close()


if __name__ == '__main__':
    ''' Main '''

    # モデルを定義
    # 回転機の質量
    m = 0.1

    # 軸受条件:剛性と減衰
    k = 100.0
    c = 0.1

    # 重心ずれ（G点からepsilonを設定）
    xg = 0.001
    yg = 0.001
    epsilon = np.sqrt(xg ** 2 + yg ** 2)

    # 回転数:N[rpm], omega[rad/s]
    N = 100
    omega = 2 * np.pi * (N / 60)

    # 解析時間
    dt = 1e-3
    t_max = 100.0
    t = np.arange(0.0, t_max, dt)

    # 初期条件
    x0 = 0.0
    y0 = 0.0
    x_dot0 = 0.0
    y_dot0 = 0.0
    pulse0 = 0.0
    pulse_dot0 = 0.0
    var = [x0, y0, x_dot0, y_dot0, pulse0, pulse_dot0]

    # 微分方程式の近似解法（過渡応答）
    var = odeint(f, var, t, args=(m, k, c, epsilon, omega))

    # 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)
    x = var.T[0]
    y = var.T[1]
    pulse = var.T[4]

    # プロット
    plot(t, x, y, pulse, N)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

import numpy as np

from matplotlib import pyplot as plt

from scipy.integrate import odeint

def f(var, t, m, k, c, epsilon, omega):

''' 運動方程式：回転機のアンバランス振動 '''

# xとy、変位と速度に分ける

x = var[0]

y = var[1]

x_dot = var[2]

y_dot = var[3]

# 回転パルスの変数を抽出

pulse = var[4]

pulse_dot = var[5]

# 運動方程式

x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x

y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

# 回転パルスの2階微分

pulse_ddot = - omega ** 2 * np.cos(omega * t)

# 結果

output = [x_dot, y_dot, x_ddot, y_ddot, pulse_dot, pulse_ddot]

return output

def plot(t, x, y, pulse, N):

''' Plot '''

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure(figsize=(10, 5))

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = ax1.twinx()

# 軸のラベルを設定する。

ax1.set_xlabel('t[s]')

ax1.set_ylabel('Displacement[m]')

ax2.set_xlabel('t[s]')

ax2.set_ylabel('Pulse[V]')

# 回転数から周期を計算（データ抽出用）

freq = N / 60

cycle = 1 / freq

dt = t[1]

sample_cycle = int(cycle / dt)

size = len(t)

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

ax1.plot(t[size - 2 * sample_cycle::], x[size - 2 * sample_cycle::], label='x', lw=3, color='red')

ax1.plot(t[size - 2 * sample_cycle::], y[size - 2 * sample_cycle::], label='y', lw=3, color='blue')

ax2.plot(t[size - 2 * sample_cycle::], pulse[size - 2 * sample_cycle::], label='pulse', lw=1, color='black')

# 凡例をまとめて出力する

handler1, label1 = ax1.get_legend_handles_labels()

handler2, label2 = ax2.get_legend_handles_labels()

ax1.legend(handler1 + handler2, label1 + label2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

if __name__ == '__main__':

''' Main '''

# モデルを定義

# 回転機の質量

m = 0.1

# 軸受条件:剛性と減衰

k = 100.0

c = 0.1

# 重心ずれ（G点からepsilonを設定）

xg = 0.001

yg = 0.001

epsilon = np.sqrt(xg ** 2 + yg ** 2)

# 回転数:N[rpm], omega[rad/s]

N = 100

omega = 2 * np.pi * (N / 60)

# 解析時間

dt = 1e-3

t_max = 100.0

t = np.arange(0.0, t_max, dt)

# 初期条件

x0 = 0.0

y0 = 0.0

x_dot0 = 0.0

y_dot0 = 0.0

pulse0 = 0.0

pulse_dot0 = 0.0

var = [x0, y0, x_dot0, y_dot0, pulse0, pulse_dot0]

# 微分方程式の近似解法（過渡応答）

var = odeint(f, var, t, args=(m, k, c, epsilon, omega))

# 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)

x = var.T[0]

y = var.T[1]

pulse = var.T[4]

# プロット

plot(t, x, y, pulse, N)

こちらが結果です。回転パルスと回転機のアンバランス振動（x変位）は同相であることが確認されました。

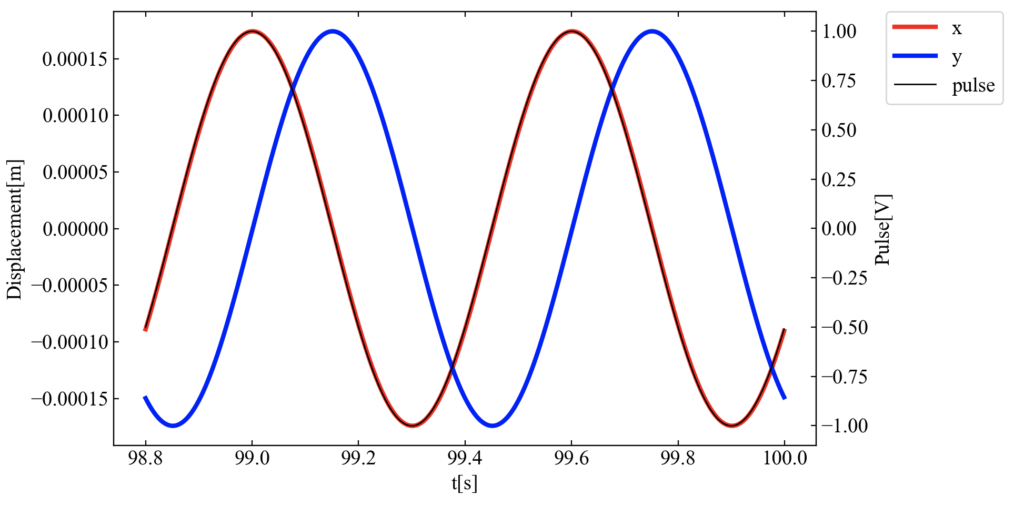
ちなみにmatplotlibの2軸描画や、2軸描画をした場合の凡例設定は以下の外部サイトを参考にしています。
・Matplotlib-2軸グラフの書き方

共振影響を確認する

先ほどは回転数100[rpm]程度の計算結果でしたが、今度は300[rpm]と回転数を上げてみましょう。事前に回転数違いの計算結果を確認しておき、この系は300rpm程度で共振するということはわかっているものとします。

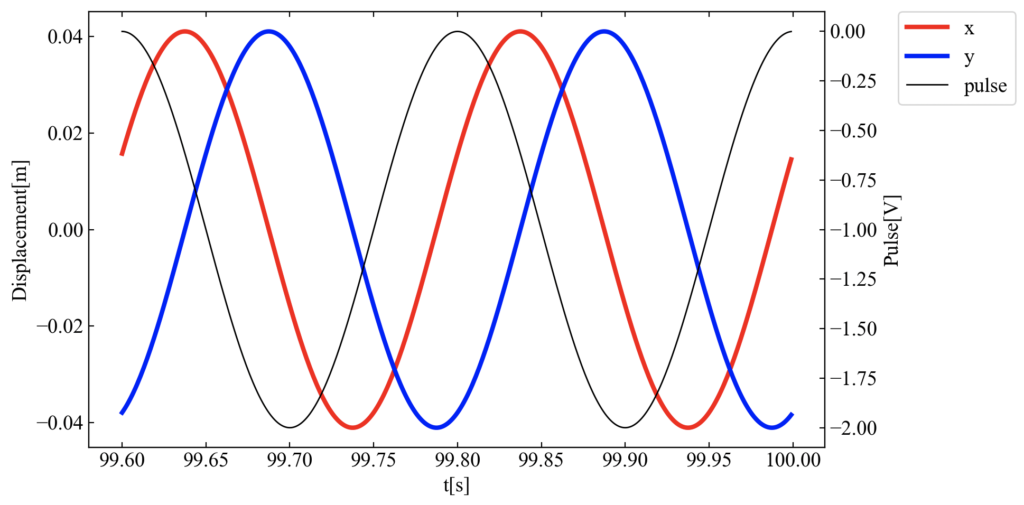
下図が結果です。回転パルスと振動の位相差が確認されました。参考書\(^{[1]}\)の通りです。

トリガー検出を実装して位相ずれをアニメーションにするPythonコード

トリガー検出

より実験と同じ状況をシミュレーションで再現するため、解析で得られた回転パルスの信号をトリガー検出してみましょう。トリガー検出とは、信号の立ち上がりや立ち下がりをプログラム的に検出することで、意図したタイミングでデータを抽出するために使います。

過去に以下の記事でトリガー検出をPythonで実装してみましたので、それをちょっといじってみます。
・Pythonで時間波形のトリガ検出アルゴリズムを作る！

全コード

「if np.sign(data[i - 1]) != np.sign(data[i]):」でトリガーを検出していますが、「j = data[i - 1] > data[i]」を使って立ち上がりの時だけに着目しています。このコードはimgフォルダの中に「N_list = np.arange(10, 600, 10)」で作成した回転数条件分の計算結果を保存し、gif画像result.gifを生成します。

import numpy as np
from matplotlib import pyplot as plt
from scipy.integrate import odeint
from PIL import Image
import os
import glob


def f(var, t, m, k, c, epsilon, omega):
    ''' 運動方程式：回転機のアンバランス振動 '''

    # xとy、変位と速度に分ける
    x = var[0]
    y = var[1]
    x_dot = var[2]
    y_dot = var[3]

    # 回転パルスの変数を抽出
    pulse = var[4]
    pulse_dot = var[5]

    # 運動方程式
    x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x
    y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

    # 回転パルスの2階微分
    pulse_ddot = - omega ** 2 * np.cos(omega * t)

    # 結果
    output = [x_dot, y_dot, x_ddot, y_ddot, pulse_dot, pulse_ddot]

    return output


def trigger(data, Tlevel):
    ''' トリガーをかける '''

    data = data - Tlevel  # 波形全体をトリガレベルでオフセット

    # 位置情報 i と判定値 jを初期化
    i = 0
    j = True

    # ゼロクロス点探査Whileループ
    # ループ停止条件＝トリガを検出した場合と検出されなかった場合のどちらか
    while j == True:

        # 最初のループはiを増分させるだけ
        if i == 0:
            i = i + 1

        # 波形を全て探査した場合はjを強制的に判定値jをFalseにしてiに-1（未検出の意味）を代入
        elif i + 1 == len(data):
            j = False
            i = -1
        # 前の値(i-1)と今の値(i)で符号を比較し判定値jに渡す。iを増分させる。
        else:
            if np.sign(data[i - 1]) != np.sign(data[i]):
                j = data[i - 1] > data[i]
            i = i + 1

    return i


def plot(t, x, y, pulse, N, dir_name, index):
    ''' Plot '''

    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure(figsize=(10, 5))
    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')
    ax2 = ax1.twinx()

    # 軸のラベルを設定する。
    ax1.set_xlabel('t[s]')
    ax1.set_ylabel('Displacement[m]')
    ax2.set_xlabel('t[s]')
    ax2.set_ylabel('Pulse[V]')

    # スケール
    ax1.set_ylim(-0.04, 0.04)

    # 回転数から周期を計算（データ抽出用）
    freq = N / 60
    cycle = 1 / freq
    dt = t[1]
    sample_cycle = int(cycle / dt)
    size = len(t)

    # 時間波形調節：最終点から4周期分を抽出
    pulse = pulse[size - 4 * sample_cycle::]
    x = x[size - 4 * sample_cycle::]
    y = y[size - 4 * sample_cycle::]

    # 時間波形調節：パルス波形でトリガーをかけ、トリガー点から2周期分を抽出
    trigger_i = trigger(pulse, 0.5)
    pulse = pulse[trigger_i:trigger_i + 2 * sample_cycle:]
    x = x[trigger_i:trigger_i + 2 * sample_cycle:]
    y = y[trigger_i:trigger_i + 2 * sample_cycle:]
    t_axis = np.arange(0, len(x) * t[1], t[1])

    # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
    ax1.plot(t_axis, x, label='x', lw=3, color='red')
    ax1.plot(t_axis, y, label='y', lw=3, color='blue')
    ax2.plot(t_axis, pulse, label='pulse', lw=1, color='black')
    ax2.text(0, 1.2, 'N=' + str(np.round(N, 1)) + '[rpm]')

    # 凡例をまとめて出力する
    handler1, label1 = ax1.get_legend_handles_labels()
    handler2, label2 = ax2.get_legend_handles_labels()
    ax1.legend(handler1 + handler2, label1 + label2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

    # レイアウト設定
    fig.tight_layout()

    # 画像を保存する。
    # dirフォルダが無い時に新規作成
    if os.path.exists(dir_name):
        pass
    else:
        os.mkdir(dir_name)

    # 画像保存パスを準備
    path = os.path.join(*[dir_name, str("{:05}".format(index)) + '.png'])

    # 画像を保存する
    plt.savefig(path)

    # グラフを表示する。
    #plt.show()
    plt.close()


def create_gif(in_dir, out_filename):
    ''' imgフォルダの複数画像からGIF画像を作る '''

    # ファイルパスをソートしてリストする
    path_list = sorted(glob.glob(os.path.join(*[in_dir, '*'])))

    # ファイルのフルパスからファイル名と拡張子を抽出
    imgs = []
    for i in range(len(path_list)):
        img = Image.open(path_list[i])
        imgs.append(img)

    # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。
    imgs[0].save(out_filename,
                 save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0)

    return


if __name__ == '__main__':
    ''' Main '''

    # モデルを定義
    # 回転機の質量
    m = 0.1

    # 軸受条件:剛性と減衰
    k = 100.0
    c = 0.1

    # 重心ずれ（G点からepsilonを設定）
    xg = 0.001
    yg = 0.001
    epsilon = np.sqrt(xg ** 2 + yg ** 2)

    # 回転数:N[rpm], omega[rad/s]
    #N = 300
    N_list = np.arange(10, 600, 10)

    # 解析時間
    dt = 1e-3
    t_max = 100.0
    t = np.arange(0.0, t_max, dt)

    for i in range(len(N_list)):

        # 初期条件
        x0 = 0.0
        y0 = 0.0
        x_dot0 = 0.0
        y_dot0 = 0.0
        pulse0 = 0.0
        pulse_dot0 = 0.0
        var = [x0, y0, x_dot0, y_dot0, pulse0, pulse_dot0]

        # 角速度
        N = N_list[i]
        omega = 2 * np.pi * (N / 60)
        print(i, N)

        # 微分方程式の近似解法（過渡応答）
        var = odeint(f, var, t, args=(m, k, c, epsilon, omega))

        # 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)
        x = var.T[0]
        y = var.T[1]
        pulse = var.T[4]

        # プロット
        dir_name = 'img'
        plot(t, x, y, pulse, N, dir_name, i)

    # GIF動画を作成する
    create_gif(dir_name, 'result.gif')

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

import numpy as np

from matplotlib import pyplot as plt

from scipy.integrate import odeint

from PIL import Image

import os

import glob

def f(var, t, m, k, c, epsilon, omega):

''' 運動方程式：回転機のアンバランス振動 '''

# xとy、変位と速度に分ける

x = var[0]

y = var[1]

x_dot = var[2]

y_dot = var[3]

# 回転パルスの変数を抽出

pulse = var[4]

pulse_dot = var[5]

# 運動方程式

x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x

y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

# 回転パルスの2階微分

pulse_ddot = - omega ** 2 * np.cos(omega * t)

# 結果

output = [x_dot, y_dot, x_ddot, y_ddot, pulse_dot, pulse_ddot]

return output

def trigger(data, Tlevel):

''' トリガーをかける '''

data = data - Tlevel # 波形全体をトリガレベルでオフセット

# 位置情報 i と判定値 jを初期化

i = 0

j = True

# ゼロクロス点探査Whileループ

# ループ停止条件＝トリガを検出した場合と検出されなかった場合のどちらか

while j == True:

# 最初のループはiを増分させるだけ

if i == 0:

i = i + 1

# 波形を全て探査した場合はjを強制的に判定値jをFalseにしてiに-1（未検出の意味）を代入

elif i + 1 == len(data):

j = False

i = -1

# 前の値(i-1)と今の値(i)で符号を比較し判定値jに渡す。iを増分させる。

else:

if np.sign(data[i - 1]) != np.sign(data[i]):

j = data[i - 1] > data[i]

i = i + 1

return i

def plot(t, x, y, pulse, N, dir_name, index):

''' Plot '''

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure(figsize=(10, 5))

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = ax1.twinx()

# 軸のラベルを設定する。

ax1.set_xlabel('t[s]')

ax1.set_ylabel('Displacement[m]')

ax2.set_xlabel('t[s]')

ax2.set_ylabel('Pulse[V]')

# スケール

ax1.set_ylim(-0.04, 0.04)

# 回転数から周期を計算（データ抽出用）

freq = N / 60

cycle = 1 / freq

dt = t[1]

sample_cycle = int(cycle / dt)

size = len(t)

# 時間波形調節：最終点から4周期分を抽出

pulse = pulse[size - 4 * sample_cycle::]

x = x[size - 4 * sample_cycle::]

y = y[size - 4 * sample_cycle::]

# 時間波形調節：パルス波形でトリガーをかけ、トリガー点から2周期分を抽出

trigger_i = trigger(pulse, 0.5)

pulse = pulse[trigger_i:trigger_i + 2 * sample_cycle:]

x = x[trigger_i:trigger_i + 2 * sample_cycle:]

y = y[trigger_i:trigger_i + 2 * sample_cycle:]

t_axis = np.arange(0, len(x) * t[1], t[1])

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

ax1.plot(t_axis, x, label='x', lw=3, color='red')

ax1.plot(t_axis, y, label='y', lw=3, color='blue')

ax2.plot(t_axis, pulse, label='pulse', lw=1, color='black')

ax2.text(0, 1.2, 'N=' + str(np.round(N, 1)) + '[rpm]')

# 凡例をまとめて出力する

handler1, label1 = ax1.get_legend_handles_labels()

handler2, label2 = ax2.get_legend_handles_labels()

ax1.legend(handler1 + handler2, label1 + label2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

# レイアウト設定

fig.tight_layout()

# 画像を保存する。

# dirフォルダが無い時に新規作成

if os.path.exists(dir_name):

pass

else:

os.mkdir(dir_name)

# 画像保存パスを準備

path = os.path.join(*[dir_name, str("{:05}".format(index)) + '.png'])

# 画像を保存する

plt.savefig(path)

# グラフを表示する。

#plt.show()

plt.close()

def create_gif(in_dir, out_filename):

''' imgフォルダの複数画像からGIF画像を作る '''

# ファイルパスをソートしてリストする

path_list = sorted(glob.glob(os.path.join(*[in_dir, '*'])))

# ファイルのフルパスからファイル名と拡張子を抽出

imgs = []

for i in range(len(path_list)):

img = Image.open(path_list[i])

imgs.append(img)

# appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。

imgs[0].save(out_filename,

save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0)

return

if __name__ == '__main__':

''' Main '''

# モデルを定義

# 回転機の質量

m = 0.1

# 軸受条件:剛性と減衰

k = 100.0

c = 0.1

# 重心ずれ（G点からepsilonを設定）

xg = 0.001

yg = 0.001

epsilon = np.sqrt(xg ** 2 + yg ** 2)

# 回転数:N[rpm], omega[rad/s]

#N = 300

N_list = np.arange(10, 600, 10)

# 解析時間

dt = 1e-3

t_max = 100.0

t = np.arange(0.0, t_max, dt)

for i in range(len(N_list)):

# 初期条件

x0 = 0.0

y0 = 0.0

x_dot0 = 0.0

y_dot0 = 0.0

pulse0 = 0.0

pulse_dot0 = 0.0

var = [x0, y0, x_dot0, y_dot0, pulse0, pulse_dot0]

# 角速度

N = N_list[i]

omega = 2 * np.pi * (N / 60)

print(i, N)

# 微分方程式の近似解法（過渡応答）

var = odeint(f, var, t, args=(m, k, c, epsilon, omega))

# 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)

x = var.T[0]

y = var.T[1]

pulse = var.T[4]

# プロット

dir_name = 'img'

plot(t, x, y, pulse, N, dir_name, i)

# GIF動画を作成する

create_gif(dir_name, 'result.gif')

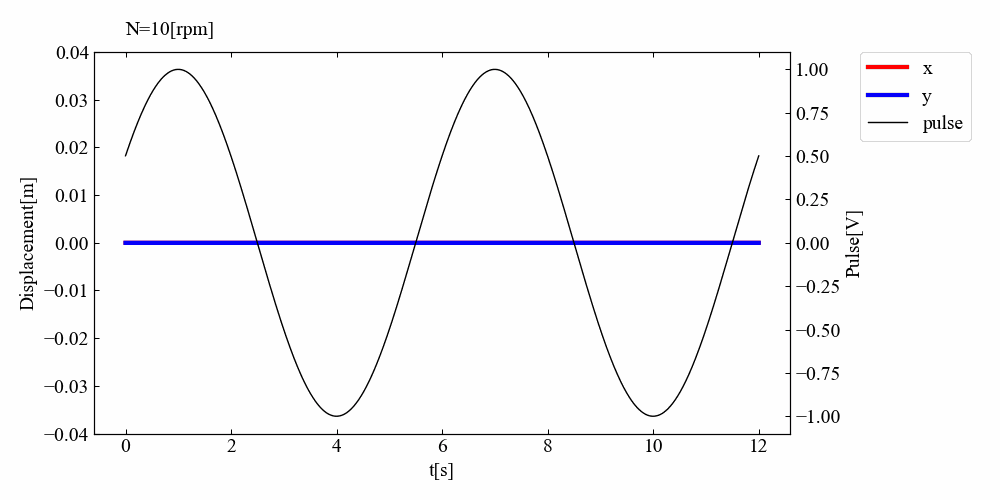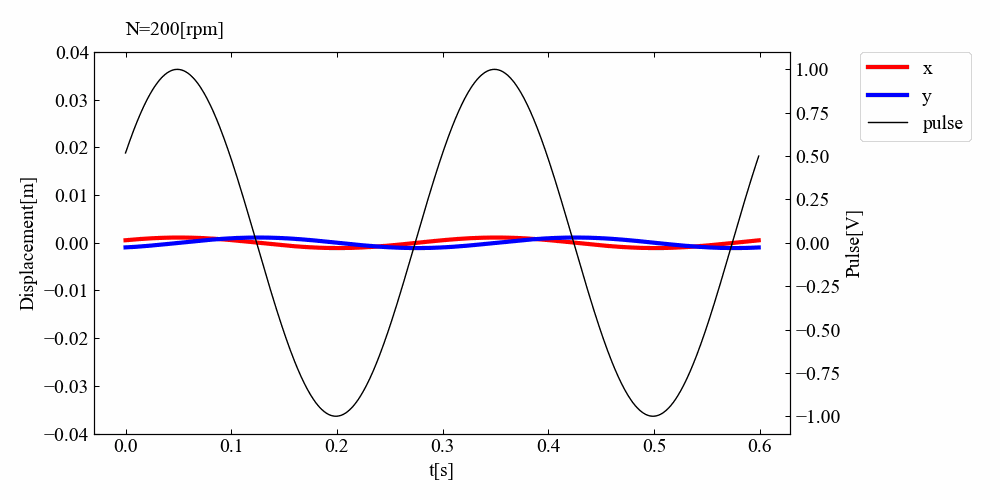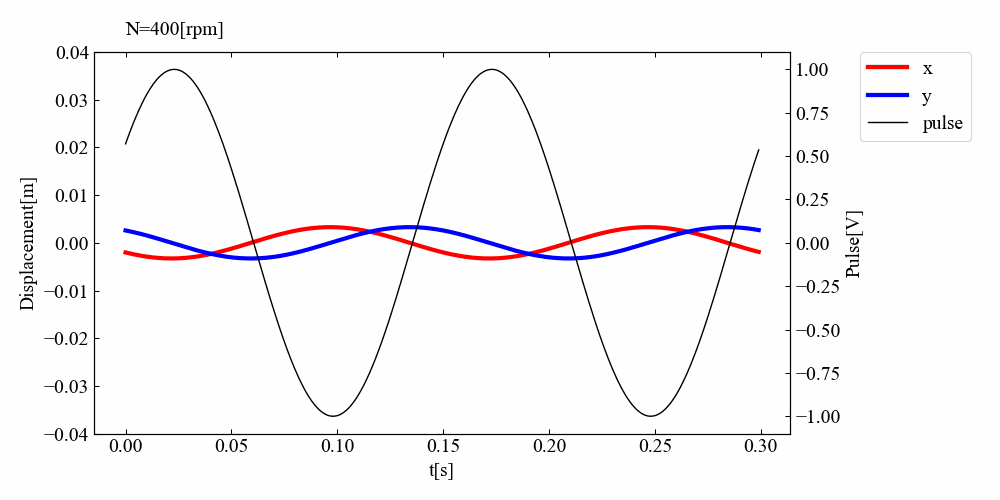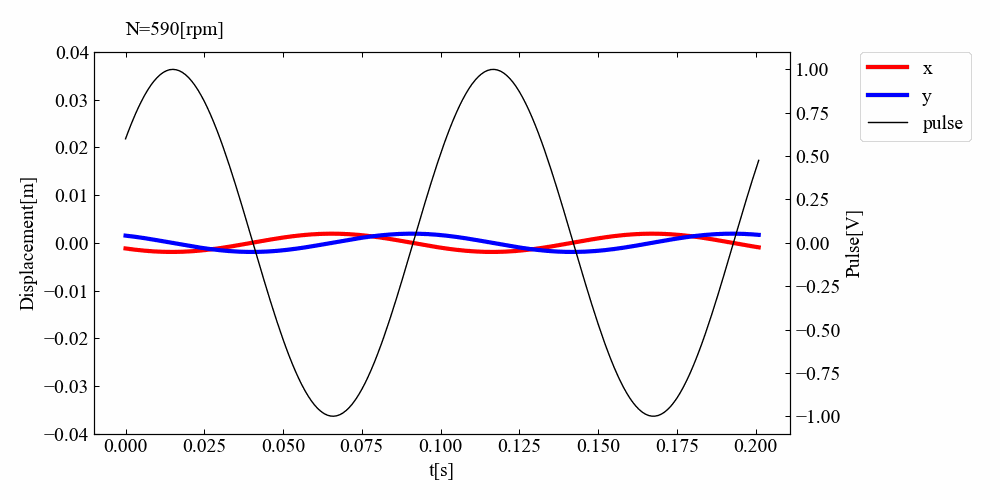
こちらが結果の動画例です。最初は変位振幅が小さく、回転パルスと変位振動の位相は同相です。しかし回転数を上げていくと徐々に変位振幅が増大し位相が90度ずれ、共振を過ぎると位相が180度になっている結果を確認できました。この一連の流れは参考書\(^{[1]}\)通りであり、シミュレーションは正常に行われたと考えられます。

まとめ

この記事はここまでです。前回のアンバランス振動シミュレーションに回転パルスとして余弦波を追加してみました。回転パルスは厳密に模擬しようとすると級数展開したりして矩形波をつくるのが良いのかも知れませんが、実際は余弦波で十分です。

回転パルスをつくるということはその後の信号処理でトリガー検出をすることが一般的です。今回は過去記事を参考にしながらトリガー検出部分も実装してみました。

まだまだ簡単なことしかしていませんが、参考書「回転機の振動」に載っていることがシミュレーションで確認されていくのは面白いと思います。

参考文献

[1]:松下修己, 田中正人, 神吉博, 小林正生, 回転機械の振動実用的振動解析の基本, コロナ社, 2011, pp27

これで実験のような位置検出シミュレーションもできそうですね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

回転機の振動シミュレーションで回転パルスを設定してみた

回転パルスをシミュレーションで再現する理由

回転機シミュレーションのおさらい

バランス修正には回転パルスの計測が重要

共振が発生すると位相がずれる

SciPyのodeintで回転パルスを追加するPythonコード

動作環境

全コード

共振影響を確認する

トリガー検出を実装して位相ずれをアニメーションにするPythonコード

トリガー検出

全コード

まとめ

参考文献

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

回転パルスをシミュレーションで再現する理由

回転機シミュレーションのおさらい

バランス修正には回転パルスの計測が重要

共振が発生すると位相がずれる

SciPyのodeintで回転パルスを追加するPythonコード

動作環境

全コード

共振影響を確認する

トリガー検出を実装して位相ずれをアニメーションにするPythonコード

トリガー検出

全コード

まとめ

参考文献

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル