回転機のアンバランス振動をシミュレートするPythonコード

工業製品である回転機はアンバランスを修正することで精密な回転を実現しています。しかし、アンバランスを真に0にすることは難しく、不釣り合い振動の影響をシミュレーションすることは重要です。ここではPythonのscipy.odeintを使ってアンバランス振動を解析する方法を紹介します。

こんにちは。wat(@watlablog)です。ここでは回転機のアンバランス振動について調べたり解析したりした結果をまとめてみます！

目次（項目クリックでジャンプできます）

回転機のアンバランス振動の概要

多くの回転機はアンバランス振動の課題がある

筆者は回転機を扱う企業に所属していますが、これまで振動問題は1次元の多自由度ばねマスダンパー系で考察したり、汎用の有限要素法ソルバーを使って検討していました。
しかしアンバランス（Unbalance）を真面目に議論するためにはロータダイナミクスを扱う必要があると感じ、まずは基礎的なことから記事にまとめていこうと思います。

アンバランス振動の運動方程式

想定する問題

ここでは最も基礎的なアンバランス振動として、水平面下で回転する重力やジャイロ効果の影響を無視した回転機モデルを考えます。

下図は\(xy\)座標系上に配置させた回転機モデルです。ここで\(S\)がモデルの図心であるのに対し、\(G\)は回転体に取り付けられた付加質量で半径方向に\(\epsilon\)だけずれた重心（Center of gravity）を指します。回転体は角速度\(\omega\)で回転し、アンバランスを持つ重心\(G\)の角度\(\theta\)は\(\omega t\)で表現されます\(^{[1]}\)。

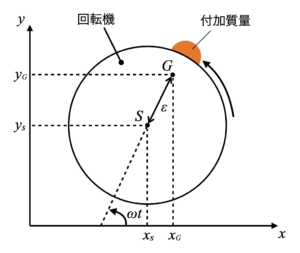
ちなみにアンバランス量の単位は質量と長さの積で示し、[gmm]や[gcm]で表します。バランスを修正するために回転機に修正錘を取り付けますが、この次元で表された数値を使ってカウンター質量と取り付け位置を選定します。

力学モデル

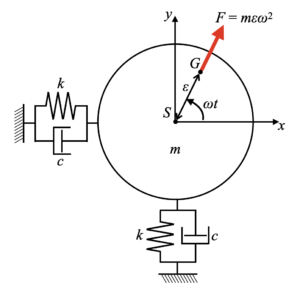
運動方程式を導出するために、先ほどの回転機モデルを想定した力学モデルを下図に示します。

軸受を想定したばねとダンパーを設置し、それぞればね定数\(k\)と減衰係数\(c\)を持ちます。
回転機は重心ずれから半径方向に角速度の2乗に比例した遠心力\(F\)が働き、この力によって\(xy\)平面に設置されたばねとダンパーに変位が発生するというモデル化です。

運動方程式

上記力学モデルにおいて、重心\(G\)の座標と2階までの導関数を式（1）〜（3）で示します。

\[ \left\{\begin{matrix} x_{G} &=& x + \epsilon \cos \omega t \\ y_{G} &=& y + \epsilon \sin \omega t \end{matrix}\right. \tag{1} \]

\[ \left\{\begin{matrix} \dot{x}_{G} &=& \dot{x} - \omega \epsilon \sin \omega t \\ \dot{y}_{G} &=& \dot{y} + \omega \epsilon \cos \omega t \end{matrix}\right. \tag{2} \]

\[ \left\{\begin{matrix} \ddot{x}_{G} &=& \ddot{x} - \omega^{2} \epsilon \cos \omega t \\ \ddot{y}_{G} &=& \ddot{y} - \omega^{2} \epsilon \sin \omega t \end{matrix}\right. \tag{3} \]

また回転軸の図心\(S\)の変位や速度によってばねの反力や減衰力が発生するため、ロータの運動方程式は式（4）で表します。運動方程式の立て方が曖昧な人は「Pythonで計算するために多自由度振動系を行列形式にする方法」に詳細な説明を書いていますので、是非ご覧ください。

\[ \left\{\begin{matrix} m\ddot{x}_{G} = - kx - c\dot{x}\\ m\ddot{y}_{G} = - ky - c\dot{y} \end{matrix}\right. \tag{4} \]

式（4）に式（2）と式（3）で計算した導関数を代入し展開すると式（5）を得ます。

\[ \left\{\begin{matrix} m\ddot{x} + c\dot{x} + kx = m \epsilon \omega^{2} \cos \omega t \\ m\ddot{y} + c\dot{y} + ky = m \epsilon \omega^{2} \sin \omega t \end{matrix}\right. \tag{5} \]

ここまで準備できればPythonによるシミュレーションは簡単にできますが、\(x, y\)の2つの運動方程式を複素変位\(z=x + jy\)を使うことによってさらに簡単にできます。つまり\(x\)と\(y\)が\(\cos\)と\(\sin\)の関係であることから、オイラーの公式（\(e^{j\omega t}=\cos \omega t + j \sin \omega t\)）を使って式（5）は式（6）になります。

\[ m\ddot{z} + c\dot{z} + kz = m\epsilon \omega^{2} e^{j\omega t} \tag{6} \]

これで準備が整いましたので、Pythonでコードを書いていきましょう！

Pythonによるアンバランス振動シミュレーションコード

動作環境

この記事のコードは以下のPython環境で動作を確認しました。

Python	Python 3.9.6
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.21.1
Scipy	1.4.1
matplotlib	3.4.3

2方向の時間波形を確認するコード

Pythonコードではscipyというライブラリのodeintを使って微分方程式を数値計算します。odeintは以下の記事で振動問題を解いた時に使いましたので、基本的な使い方をおさらいしたい場合は是非ご覧ください。
・Pythonで多自由度振動系の過渡応答計算をする時はSciPyを使おう

今回のコードにおける設定は以下のとおりです。是非条件を変更してみてください。

回転機の質量\(m\)
上に示した力学モデルにおいて、2つのばねとダンパーが繋がった丸部分質量を設定します。
ばね定数\(k\)と減衰係数\(c\)
軸受の剛性と粘性減衰係数です。実験ができるのであれば、軸に対しロータを平面方向に変位させた時の荷重からばね定数を計算できると良いかもしれません。
重心ずれ\(\epsilon\)
アンバランス振動が発生する原因となる重心ずれは最終的には\(\epsilon\)が必要ですが、イメージしやすいように重心の座標\((x_{G}, y_{G})\)から計算するようにしてみました。
回転数\(N\)
回転数は1分間に何回転するかを示す[rpm]で指定します。
初期条件\(x_{0}, y_{0}, \dot{x}_{0}, \dot{y}_{0}\)
2方向の変位と速度について初期条件を与えますが、静止状態を想定して全て0にしています。
解析条件\(dt, t_{max}\)
シミュレーションは時間刻み\(dt\)と最大解析時間\(t_{max}\)を指定します。今回のデフォルトの条件は回転数\(N\)=1[rpm]なので、60[s]で1周期の波が見れるはずです。条件によって解析条件も変更しましょう。

コピペで動作する全コードはこちら。関数fで運動方程式を設定しています。式（6）の複素変位を使った処理は便利なのですが、scipyのodeintが複素数を処理できないことで式（5）のまま解いています。

import numpy as np
from matplotlib import pyplot as plt
from scipy.integrate import odeint


def f(var, t, m, k, c, epsilon, omega):
    ''' 運動方程式：回転機のアンバランス振動 '''

    # xとy、変位と速度に分ける
    x = var[0]
    y = var[1]
    x_dot = var[2]
    y_dot = var[3]

    # 運動方程式
    x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x
    y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

    # 結果
    output = [x_dot, y_dot, x_ddot, y_ddot]

    return output


def plot(t, x, y):
    ''' Plot '''

    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure()
    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')

    # 軸のラベルを設定する。
    ax1.set_xlabel('t[s]')
    ax1.set_ylabel('Displacement[m]')

    # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
    ax1.plot(t, x, label='x', lw=1, color='red')
    ax1.plot(t, y, label='y', lw=1, color='blue')
    ax1.legend()

    # レイアウト設定
    fig.tight_layout()

    # グラフを表示する。
    plt.show()
    plt.close()


if __name__ == '__main__':
    ''' Main '''

    # モデルを定義
    # 回転機の質量
    m = 0.1

    # 軸受条件:剛性と減衰
    k = 1.0
    c = 1.0

    # 重心ずれ（G点からepsilonを設定）
    xg = 0.001
    yg = 0.001
    epsilon = np.sqrt(xg ** 2 + yg ** 2)

    # 回転数:N[rpm], omega[rad/s]
    N = 1
    omega = 2 * np.pi * (N / 60)

    # 解析時間
    dt = 1e-3
    t_max = 100.0
    t = np.arange(0.0, t_max, dt)

    # 初期条件
    x0 = 0.0
    y0 = 0.0
    x_dot0 = 0.0
    y_dot0 = 0.0
    var = [x0, y0, x_dot0, y_dot0]

    # 微分方程式の近似解法（過渡応答）
    var = odeint(f, var, t, args=(m, k, c, epsilon, omega))

    # 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)
    x = var.T[0]
    y = var.T[1]

    # プロット
    plot(t, x, y)

import numpy as np

from matplotlib import pyplot as plt

from scipy.integrate import odeint

def f(var, t, m, k, c, epsilon, omega):

''' 運動方程式：回転機のアンバランス振動 '''

# xとy、変位と速度に分ける

x = var[0]

y = var[1]

x_dot = var[2]

y_dot = var[3]

# 運動方程式

x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x

y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

# 結果

output = [x_dot, y_dot, x_ddot, y_ddot]

return output

def plot(t, x, y):

''' Plot '''

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('t[s]')

ax1.set_ylabel('Displacement[m]')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

ax1.plot(t, x, label='x', lw=1, color='red')

ax1.plot(t, y, label='y', lw=1, color='blue')

ax1.legend()

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

if __name__ == '__main__':

''' Main '''

# モデルを定義

# 回転機の質量

m = 0.1

# 軸受条件:剛性と減衰

k = 1.0

c = 1.0

# 重心ずれ（G点からepsilonを設定）

xg = 0.001

yg = 0.001

epsilon = np.sqrt(xg ** 2 + yg ** 2)

# 回転数:N[rpm], omega[rad/s]

N = 1

omega = 2 * np.pi * (N / 60)

# 解析時間

dt = 1e-3

t_max = 100.0

t = np.arange(0.0, t_max, dt)

# 初期条件

x0 = 0.0

y0 = 0.0

x_dot0 = 0.0

y_dot0 = 0.0

var = [x0, y0, x_dot0, y_dot0]

# 微分方程式の近似解法（過渡応答）

var = odeint(f, var, t, args=(m, k, c, epsilon, omega))

# 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)

x = var.T[0]

y = var.T[1]

# プロット

plot(t, x, y)

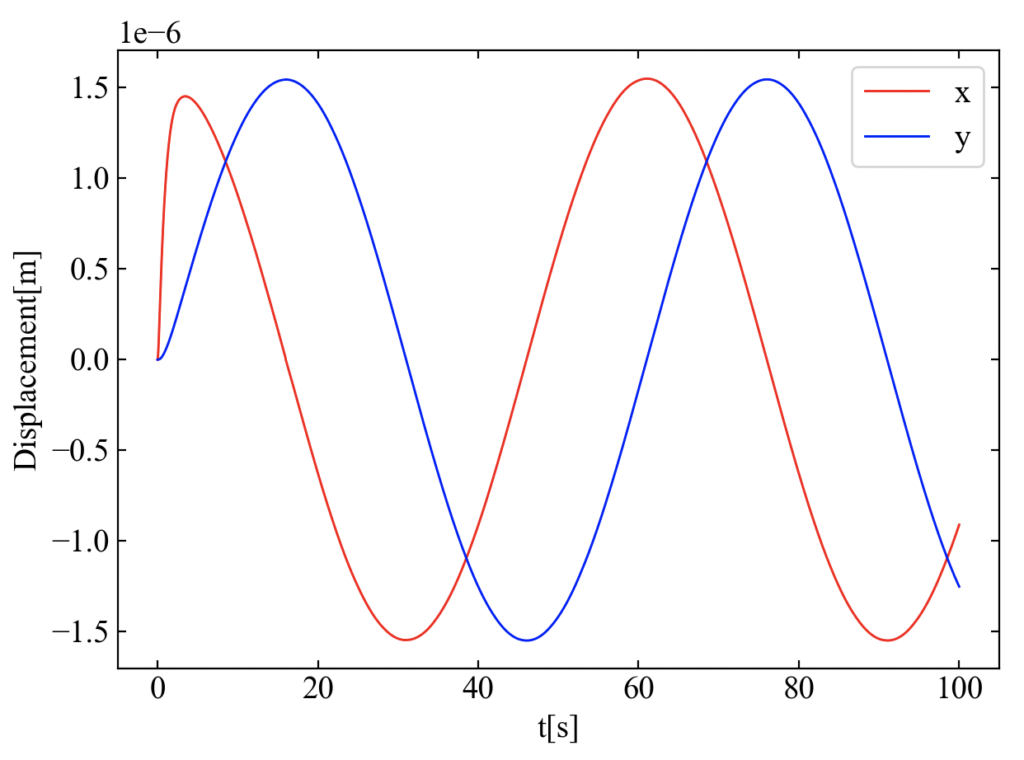
シミュレーション結果を以下に示します。まずは\(x,y\)方向の時間波形をmatplotlibで表示させてみました。

回転数をスイープさせるシミュレーションコード

先ほどは一定の回転数におけるアンバランス振動を解析してみましたが、回転機は始動から定常回転に至るまで徐々にスピードアップするものです。回転数が変化していく過程で、回転数と構造物の固有振動数が一致すると振幅の増大を引き起こします。

以下のコードは初期回転数N0と最大回転数N_maxを指定し、運動方程式の回転数変化を表現したPythonコードです。ここでは解析の終了時間でN_maxとなる仕様です。

import numpy as np
from matplotlib import pyplot as plt
from scipy.integrate import odeint


def f(var, t, m, k, c, epsilon, omega0, grad):
    ''' 運動方程式：回転機のアンバランス振動 '''

    # xとy、変位と速度に分ける
    x = var[0]
    y = var[1]
    x_dot = var[2]
    y_dot = var[3]

    # 回転数スイープ式
    omega = grad * t + omega0

    # 運動方程式
    x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x
    y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

    # 結果
    output = [x_dot, y_dot, x_ddot, y_ddot]

    return output


def plot(t, x, y, N):
    ''' Plot '''

    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure()
    ax1 = fig.add_subplot(211)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')
    ax2 = fig.add_subplot(212)
    ax2.yaxis.set_ticks_position('both')
    ax2.xaxis.set_ticks_position('both')

    # 軸のラベルを設定する。
    ax1.set_xlabel('t[s]')
    ax1.set_ylabel('Displacement[m]')
    ax2.set_xlabel('t[s]')
    ax2.set_ylabel('N[rpm]')

    # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。
    ax1.plot(t, x, label='x', lw=1, color='red')
    ax1.plot(t, y, label='y', lw=1, color='blue')
    ax1.legend()
    ax2.plot(t, N, label='N', lw=1, color='red')

    # レイアウト設定
    fig.tight_layout()

    # グラフを表示する。
    plt.show()
    plt.close()


if __name__ == '__main__':
    ''' Main '''

    # モデルを定義
    # 回転機の質量
    m = 0.1

    # 軸受条件:剛性と減衰
    k = 100.0
    c = 0.1

    # 重心ずれ（G点からepsilonを設定）
    xg = 0.001
    yg = 0.001
    epsilon = np.sqrt(xg ** 2 + yg ** 2)

    # 解析時間
    dt = 1e-3
    t_max = 100.0
    t = np.arange(0.0, t_max, dt)

    # 回転数:N[rpm], omega[rad/s], 0:初期回転数, max:最大回転数
    N0 = 1
    N_max = 300
    omega0 = 2 * np.pi * (N0 / 60)
    omega_max = 2 * np.pi * (N_max / 60)
    grad = (omega_max - omega0) / t_max
    N_sweep = (grad * t + omega0) * (60 / (2 * np.pi))


    # 初期条件
    x0 = 0.0
    y0 = 0.0
    x_dot0 = 0.0
    y_dot0 = 0.0
    var = [x0, y0, x_dot0, y_dot0]

    # 微分方程式の近似解法（過渡応答）
    var = odeint(f, var, t, args=(m, k, c, epsilon, omega0, grad))

    # 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)
    x = var.T[0]
    y = var.T[1]

    # プロット
    plot(t, x, y, N_sweep)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

import numpy as np

from matplotlib import pyplot as plt

from scipy.integrate import odeint

def f(var, t, m, k, c, epsilon, omega0, grad):

''' 運動方程式：回転機のアンバランス振動 '''

# xとy、変位と速度に分ける

x = var[0]

y = var[1]

x_dot = var[2]

y_dot = var[3]

# 回転数スイープ式

omega = grad * t + omega0

# 運動方程式

x_ddot = epsilon * omega ** 2 * np.cos(omega * t) - (c / m) * x_dot - (k / m) * x

y_ddot = epsilon * omega ** 2 * np.sin(omega * t) - (c / m) * y_dot - (k / m) * y

# 結果

output = [x_dot, y_dot, x_ddot, y_ddot]

return output

def plot(t, x, y, N):

''' Plot '''

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(211)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = fig.add_subplot(212)

ax2.yaxis.set_ticks_position('both')

ax2.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('t[s]')

ax1.set_ylabel('Displacement[m]')

ax2.set_xlabel('t[s]')

ax2.set_ylabel('N[rpm]')

# データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。

ax1.plot(t, x, label='x', lw=1, color='red')

ax1.plot(t, y, label='y', lw=1, color='blue')

ax1.legend()

ax2.plot(t, N, label='N', lw=1, color='red')

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

if __name__ == '__main__':

''' Main '''

# モデルを定義

# 回転機の質量

m = 0.1

# 軸受条件:剛性と減衰

k = 100.0

c = 0.1

# 重心ずれ（G点からepsilonを設定）

xg = 0.001

yg = 0.001

epsilon = np.sqrt(xg ** 2 + yg ** 2)

# 解析時間

dt = 1e-3

t_max = 100.0

t = np.arange(0.0, t_max, dt)

# 回転数:N[rpm], omega[rad/s], 0:初期回転数, max:最大回転数

N0 = 1

N_max = 300

omega0 = 2 * np.pi * (N0 / 60)

omega_max = 2 * np.pi * (N_max / 60)

grad = (omega_max - omega0) / t_max

N_sweep = (grad * t + omega0) * (60 / (2 * np.pi))

# 初期条件

x0 = 0.0

y0 = 0.0

x_dot0 = 0.0

y_dot0 = 0.0

var = [x0, y0, x_dot0, y_dot0]

# 微分方程式の近似解法（過渡応答）

var = odeint(f, var, t, args=(m, k, c, epsilon, omega0, grad))

# 結果を分離(0:x変位, 1:y変位, 2:x速度, 3:y速度)

x = var.T[0]

y = var.T[1]

# プロット

plot(t, x, y, N_sweep)

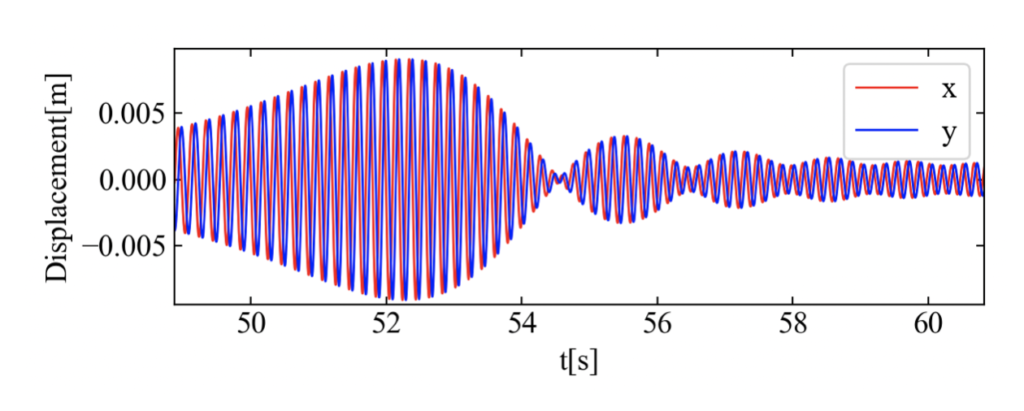
こちらがシミュレーション結果です。各変数は共振が50[s]程度の場所で発生するように微調整しました。

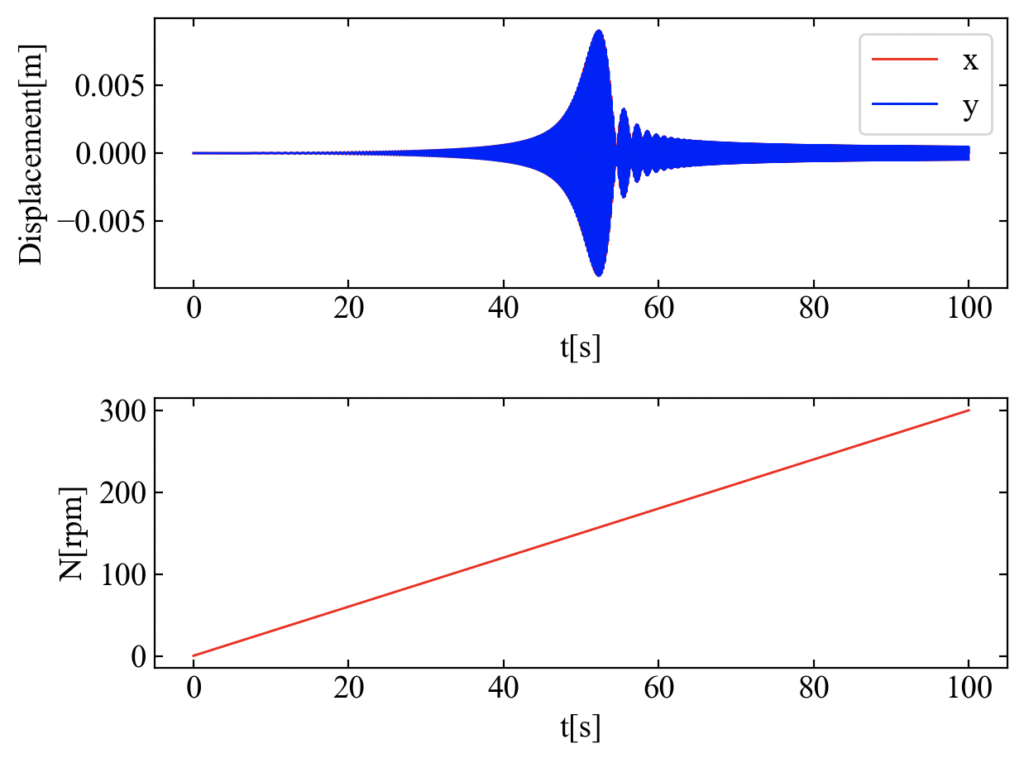
共振部周辺を拡大してみると、共振を通り過ぎたあとに振幅変調の発生が確認できます。これは参考文献\(^{[1]}\)に事例が載っており回転数のスイープ速度の影響で変化する特徴らしいです。詳しい分析は追々したいですが、まずはシミュレーション結果が参考書で書かれている内容を再現してきたので第一歩を踏み出せたとします。

まとめ

今回はここまでです。
この記事では回転機のアンバランスについて簡単に概要を紹介し、静止座標系を用いた運動方程式を導出してみました。

2つのばねとダンパーを回転機の質量に接続して振れ回り振動を解析するコードをPythonで書き、時間波形をプロットしたり、回転数変化による共振確認もできるようになりました。
回転機の振動を確認していくための入門的な記事になったと思います。

参考文献

[1]:松下修己, 田中正人, 神吉博, 小林正生, 回転機械の振動実用的振動解析の基本, コロナ社, 2011, pp23-36

回転機の振動シミュレーションをPythonで書いてみました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

回転機のアンバランス振動をシミュレートするPythonコード

回転機のアンバランス振動の概要

多くの回転機はアンバランス振動の課題がある

アンバランス振動の運動方程式

想定する問題

力学モデル

運動方程式

Pythonによるアンバランス振動シミュレーションコード

動作環境

2方向の時間波形を確認するコード

回転数をスイープさせるシミュレーションコード

まとめ

参考文献

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

回転機のアンバランス振動の概要

多くの回転機はアンバランス振動の課題がある

アンバランス振動の運動方程式

想定する問題

力学モデル

運動方程式

Pythonによるアンバランス振動シミュレーションコード

動作環境

2方向の時間波形を確認するコード

回転数をスイープさせるシミュレーションコード

まとめ

参考文献

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル