
離散フーリエ変換は単純な式で実装できる信号処理アルゴリズムです。Pythonは豊富なライブラリについ頼ってしまいますが、他の言語でも自由に実装できるように基本を学びましょう。ここではPythonであえてforループを使った離散フーリエ変換の方法を学び、次に同様の結果が得られるSwiftコードを紹介します。
こんにちは。wat(@watlablog)です。今回は基本の離散フーリエ変換式をPythonで確認しながら、iOSでも使えるようSwiftでも実装してみます!
本記事の目標とモチベーション
Swiftで離散フーリエ変換を実装する
WATLABブログでは最近iOS版の信号処理アプリ制作を目標にしています。「SwiftUIとAVFoundationで音声を再生する方法」で紹介した通り、Swiftで録音したデータを再生したりグラフに波形を表示させたりできるようになってきました。
そのため次は周波数分析を実装するためにフーリエ変換を実装することを目標とします。
ただし、離散フーリエ変換(DFT:Discrete Fourier Transform)は録音波形等の大規模サンプリングデータを扱うにはあまりおすすめできないことが注意点です。今回はあくまで感覚を掴むために、離散フーリエ変換のアルゴリズムを学ぶ記事という位置付けです。
より実用的な周波数分析には高速フーリエ変換(FFT:Fast Fourier Transform)があります。Swiftにもライブラリがあるとのことなので、この記事はその前段とします(あとで書く!)。
Pythonで検証する理由
最終目標はSwiftによる離散フーリエ変換の実装ですが、今回は最初にPythonでアルゴリズムを実装します。
あえて一度Pythonで実装するのはPythonが数式をほぼそのままの形で直感的に書けたり、プログラミング特有の知識がほぼいらないからアルゴリズムのデバッグに向いているというのが理由です。上記の特徴は本職のプログラマからすると色々賛否両論ありそうですが、簡単にグラフが書けたり数式を実装できるのはプロトタイプが作りやすく非常にありがたいです。
Pythonで離散フーリエ変換をフルスクラッチするコード
この記事は基本的なアルゴリズムを学ぶための位置付けであり、計算自体は遅いコードを紹介しています。Pythonによる実用的なDFTやFFTコードはSciPyを使った方法として以下の記事にまとめていますので、是非こちらもご覧ください。
・PythonでFFT実装!SciPyのフーリエ変換まとめ
離散フーリエ変換の式
離散フーリエ変換を式(1)に示します。ここで\(F\)は時間信号\(x\)をフーリエ変換した後のフーリエスペクトルです。\(k\)は周波数インデックス、\(n\)は標本点(時間信号のインデックス)を示し共に整数です。\(N\)は任意の自然数で通常時間信号\(x\)の総数を指します。
そして虚数\(j\)を使って指数部が構成されており、フーリエスペクトル\(F\)は複素数となります。
周波数軸は式(2)で計算されます。
式(1)による離散フーリエ変換の計算量は\(O(N^{2})\)とデータ数の二乗になります。これは録音データ処理にはなかなか適用が難しいレベルの計算量です。
PythonによるDFTコード
DFT関数部
まずは以下にdft関数を示します。この関数は時間軸tと時間信号値xを引数として、離散フーリエ変換後の周波数軸freqと振幅成分ampを返すものです。
DFTをすると信号が正の周波数軸と負の周波数軸に分散されます。振幅成分を物理的に正確になるよう求めるためにはNによるスケーリングが必要です。振幅成分のスケーリングは正と負の周波数に分散された領域では\(\frac{N}{2}\)で除算しますが、直流成分である0[Hz]のデータは\(N\)で除算します(この部分はなかなかネットに説明がなく、今回ようやく理解したところです…)。
そのため関数内ではif文を用いてスケールファクタsfを分岐させています。
NumPyにはもっと効率的な書き方がありますが、今回はアルゴリズムの理解のためにforループを使って実装してみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 |
def dft(t, x): """ 離散フーリエ変換 """ # N:データ点数、F:フーリエスペクトル(複素数)、dt:時間刻み[s]、freq:周波数軸 N = len(x) F = np.zeros(N, dtype=complex) dt = t[1] - t[0] freq = np.zeros(N, dtype=float) amp = np.zeros(N, dtype=float) # 離散フーリエ変換式と周波数軸の式 for k in range(N): for n in range(N): # フーリエスペクトル F[k] += x[n] * np.exp(-2j * np.pi * n * k / N) # 周波数軸 freq[k] = k / (N * dt) # 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)でスケーリング係数を変える。 if k == 0: sf = N else: sf = N / 2 # 振幅 amp[k] = np.sqrt(F[k].real ** 2 + F[k].imag ** 2) / sf return freq, amp |
全コード
以下に全コードを示します。matplotlibで簡単にグラフ化してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 |
import numpy as np from matplotlib import pyplot as plt def dft(t, x): """ 離散フーリエ変換 """ # N:データ点数、F:フーリエスペクトル(複素数)、dt:時間刻み[s]、freq:周波数軸 N = len(x) F = np.zeros(N, dtype=complex) dt = t[1] - t[0] freq = np.zeros(N, dtype=float) amp = np.zeros(N, dtype=float) # 離散フーリエ変換式と周波数軸の式 for k in range(N): for n in range(N): # フーリエスペクトル F[k] += x[n] * np.exp(-2j * np.pi * n * k / N) # 周波数軸 freq[k] = k / (N * dt) # 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)でスケーリング係数を変える。 if k == 0: sf = N else: sf = N / 2 # 振幅 amp[k] = np.sqrt(F[k].real ** 2 + F[k].imag ** 2) / sf return freq, amp def sample_wave(): """ サンプル波形 """ # A:変動成分振幅、f:周波数[Hz]、dc:直流成分、dt:時間刻み[s] A = 1 f = 1 dc = 1 dt = 1 / 100 # サンプル波形。t:時間軸[s]、x:時間信号 t = np.arange(0, 5, dt) x = A * np.sin(2 * np.pi * f * t) + dc return t, x def plot(t, x, freq, amp): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(7, 5)) ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('Frequency[Hz]') ax2.set_ylabel('X[m]') # スケールの設定をする。 ax2.set_xlim(0.0, 10.0) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='time', lw=1, color='red') ax2.plot(freq, amp, label='freq', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' t, x = sample_wave() freq, amp = dft(t, x) plot(t, x, freq, amp) |
実行結果の例
こちらが実行結果の例です。上記プログラムを実行すると、サンプル信号として振動数1[Hz]の正弦波を生成します。このサンプル信号は直流成分の検証を行うためにdcを加算しています。
下図の周波数波形を確認すると、0Hzと1Hzの振幅成分はプログラムで指定した値になっていることがわかりました。
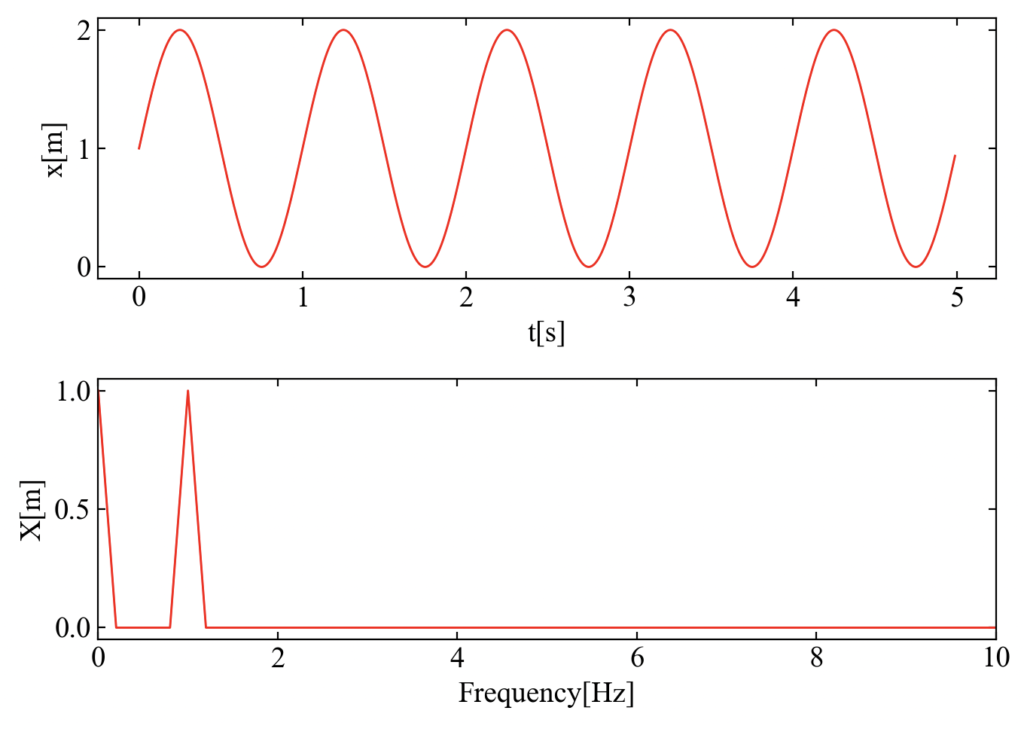
if文でスケーリング係数を変更しないと直流成分が合わない…といったことになり得るためご注意ください。
Swiftで離散フーリエ変換をフルスクラッチするコード
基本のコード:正弦波を表示させる
これからSwiftで離散フーリエ変換のコードを実装しますが、まずは基本とするコードを紹介します。
以下のコードはButtonを押すとwavePoints関数で正弦波を生成し、Chart{}でグラフ表示するだけのプログラムです。以下の記事を参考にしています。
・Swift入門:最低限覚えておく基礎文法の備忘録
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 |
import SwiftUI import Charts struct PointsData: Identifiable { // 点群データの構造体 var xValue: Float var yValue: Float var id = UUID() } struct ContentView: View { // データを定義 @State private var data: [PointsData] = [] @State private var x: [Float] = [] @State private var y: [Float] = [] func wavePoints(dt: Float, length: Float) -> (xArray: [Float], yArray: [Float]){ // プロットするデータを演算する関数 // 時間刻みdtと時間長lengthからx軸を作成 let xArray = Array(stride(from: 0.0, to: length, by: dt)) // 正弦波を作成。A:振幅、f:周波数[Hz]、dc:直流成分 let A: Float = 1 let f: Float = 1 let dc: Float = 1 let yArray = xArray.map{ A * sin(2 * .pi * f * $0) + dc } return (xArray, yArray) } var body: some View { // UI VStack{ Chart { // データ構造からx, y値を取得してプロット ForEach(data) { shape in LineMark( x: .value("x", shape.xValue), y: .value("y", shape.yValue) ) } } .padding(.all, 10) Button("Button"){ // ボタンイベント // 関数を実行してx, y演算結果を取得 let result = wavePoints(dt: 0.001, length: 5) x = result.xArray y = result.yArray // プロットデータの全削除 data.removeAll() // プロットデータの追加 for i in 0..<x.count { data.append(.init(xValue: x[i], yValue: y[i])) } } } } } struct ContentView_Previews: PreviewProvider { static var previews: some View { // プレビュー ContentView() } } |
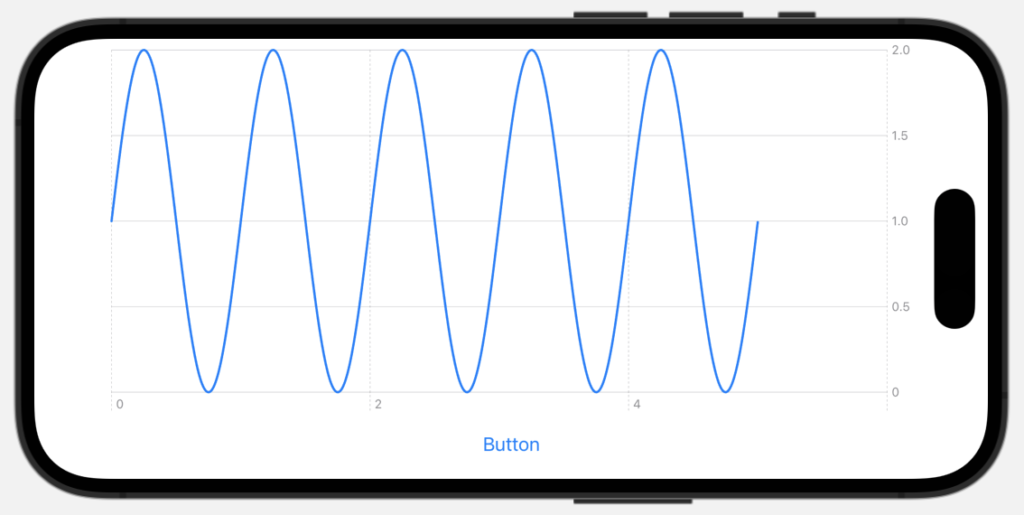
コードを実行してButtonをクリックすると以下の画面になります。正弦波が表示されました。
複素数型の構造体をつくる
離散フーリエ変換は複素数(Complex)を扱いますが、Swiftには標準で複素数型がありません。そのため自分で定義する必要があります。
Swiftにおいてユーザー定義による構造体はstructで作成します。以下のコードはSwiftで複素数を扱えるように定義した構造体です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
struct Complex { // 複素数型の構造体を定義 // re:実部、im:虚部 var re: Float var im: Float // Complex + Complexの場合の演算処理 static func +(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re + rhs.re, im: lhs.im + rhs.im) } // Complex * Complexの場合の演算処理 static func *(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re * rhs.re - lhs.im * rhs.im, im: lhs.re * rhs.im + lhs.im * rhs.re) } } |
「static func +」と「static func *」はそれぞれ加算と乗算の演算子が使われた場合の処理を意味しています。ここでそれぞれのstatic funcには「(lhs: Complex, rhs: Complex)」と書かれていますが、これは複素数が演算子の左側(Left hand side)と右側(Right hand side)に配置された場合の処理を指定しています。
離散フーリエ変換の式(1)では複素数同士の加算と乗算が使われているので、今回は最低限この部分の記述をしているというわけです。
複素数同士の加算(a+jb)+(c+jd)は実部がa+c, 虚部が(b+d)jです。Swiftでは標準で複素数型を持っていないため、この構造体の中で実部と虚部に分けて整理する…という処理をしているのですね。
仮にFloat型とDouble型の除算を定義したい時は、「static func /(lhs: Float, rhs: Double)」と書けば良いというわけです。ややこしいですが、わかれば自分で自由に構造体をつくれそうです。
Swiftによる離散フーリエ変換の関数
続いて本題の離散フーリエ変換の関数を以下に示します。何度も書きますが、この関数はアルゴリズムを学ぶための自作コードなので非常に遅いことに注意してください。別記事でライブラリを使った場合も学びます。
先ほどのPythonコードとほぼ対応させているのでコメントアウトの説明を見ていただければ内容がわかると思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
func dft(_ t: [Float], _ x: [Float]) -> ([Float], [Float]) { // 離散フーリエ変換 // N:標本数、F:フーリエスペクトル、dt:時間刻み[Hz] let N = x.count var F = [Complex](repeating: Complex(re: 0, im: 0), count: N) let dt = t[1] - t[0] // freq:周波数軸[Hz]、amp:振幅 var freq = [Float](repeating: 0, count: N) var amp = [Float](repeating: 0, count: N) // 離散フーリエ変換の式 for k in 0..<N { for n in 0..<N { // 複素指数関数の代わりにオイラーの公式で三角関数に変換して計算 let theta = -2 * .pi * Float(n * k) / Float(N) let c = Complex(re: cos(theta), im: sin(theta)) F[k] = F[k] + c * Complex(re: x[n], im: 0) } // 周波数軸 freq[k] = Float(k) / (Float(N) * dt) // 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)で // スケーリング係数を変える。 let sf: Float if k == 0 { sf = Float(N) } else { sf = Float(N) / 2 } // 振幅 amp[k] = sqrt(F[k].re * F[k].re + F[k].im * F[k].im) / sf } return (freq, amp) } |
Pythonは複素数を標準で扱えるため複素指数関数としてネイピア数の冪計算をしていましたが、Swiftでは先の理由から複素指数関数の構造体を作るか工夫しなければなりません。最も簡単なのはオイラーの公式で複素指数関数を実数の余弦関数と虚数の正弦関数に変換する方法です。
先ほどのコードは式(3)を使っています。
全コード例
コピペ可能な全コードを以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 |
import SwiftUI import Charts struct PointsData: Identifiable { // 点群データの構造体 var xValue: Float var yValue: Float var id = UUID() } struct ContentView: View { // データを定義 @State private var data: [PointsData] = [] @State private var x: [Float] = [] @State private var y: [Float] = [] func wavePoints(dt: Float, length: Float) -> (xArray: [Float], yArray: [Float]){ // プロットするデータを演算する関数 // 時間刻みdtと時間長lengthからx軸を作成 let xArray = Array(stride(from: 0.0, to: length, by: dt)) // 正弦波を作成。A:振幅、f:周波数[Hz]、dc:直流成分 let A: Float = 1 let f: Float = 1 let dc: Float = 1 let yArray = xArray.map{ A * sin(2 * .pi * f * $0) + dc } return (xArray, yArray) } struct Complex { // 複素数型の構造体を定義 // re:実部、im:虚部 var re: Float var im: Float // Complex + Complexの場合の演算処理 static func +(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re + rhs.re, im: lhs.im + rhs.im) } // Complex * Complexの場合の演算処理 static func *(lhs: Complex, rhs: Complex) -> Complex { return Complex(re: lhs.re * rhs.re - lhs.im * rhs.im, im: lhs.re * rhs.im + lhs.im * rhs.re) } } func dft(_ t: [Float], _ x: [Float]) -> ([Float], [Float]) { // 離散フーリエ変換 // N:標本数、F:フーリエスペクトル、dt:時間刻み[Hz] let N = x.count var F = [Complex](repeating: Complex(re: 0, im: 0), count: N) let dt = t[1] - t[0] // freq:周波数軸[Hz]、amp:振幅 var freq = [Float](repeating: 0, count: N) var amp = [Float](repeating: 0, count: N) // 離散フーリエ変換の式 for k in 0..<N { for n in 0..<N { // 複素指数関数の代わりにオイラーの公式で三角関数に変換して計算 let theta = -2 * .pi * Float(n * k) / Float(N) let c = Complex(re: cos(theta), im: sin(theta)) F[k] = F[k] + c * Complex(re: x[n], im: 0) } // 周波数軸 freq[k] = Float(k) / (Float(N) * dt) // 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)で // スケーリング係数を変える。 let sf: Float if k == 0 { sf = Float(N) } else { sf = Float(N) / 2 } // 振幅 amp[k] = sqrt(F[k].re * F[k].re + F[k].im * F[k].im) / sf } return (freq, amp) } var body: some View { // UI VStack{ Chart { // データ構造からx, y値を取得してプロット ForEach(data) { shape in LineMark( x: .value("x", shape.xValue), y: .value("y", shape.yValue) ) } } .padding(.all, 10) Button("Button"){ // ボタンイベント // 関数を実行してx, y演算結果を取得 let result = wavePoints(dt: 0.01, length: 5) x = result.xArray y = result.yArray // DFTを計算 let dftResult = dft(x, y) let freq = dftResult.0 let amp = dftResult.1 // プロットデータの全削除 data.removeAll() // プロットデータの追加 for i in 0..<x.count { data.append(.init(xValue: freq[i], yValue: amp[i])) } } } } } struct ContentView_Previews: PreviewProvider { static var previews: some View { // プレビュー ContentView() } } |
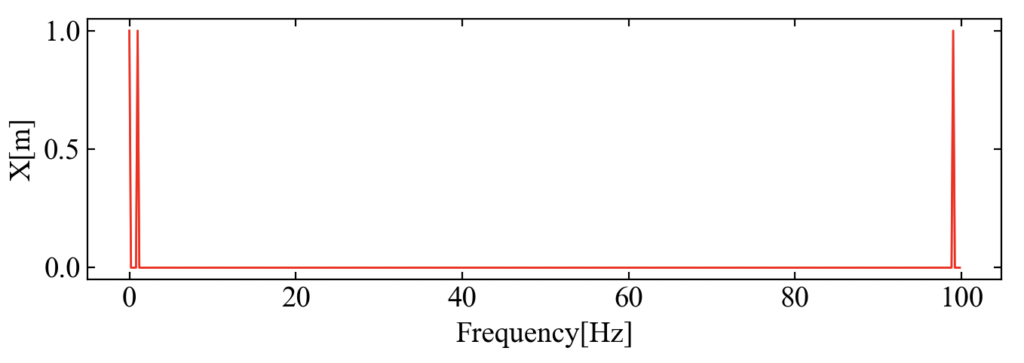
こちらがDFT計算結果です。Pythonの結果と同様に直流成分と変動成分の振幅が1になっており、さらに鏡像ピークも確認できました。
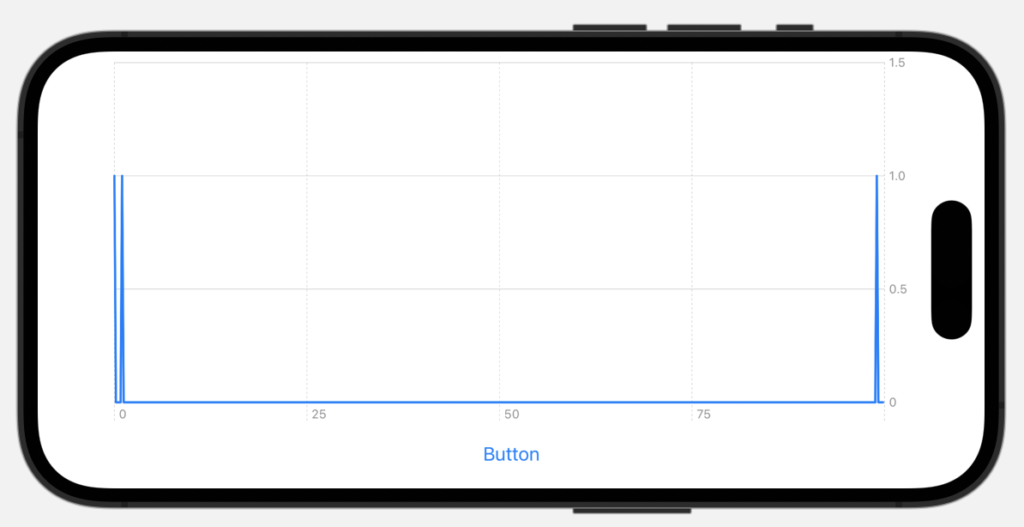
指定した1[Hz]のピークが確かに立っていることも拡大することで確認可能です。
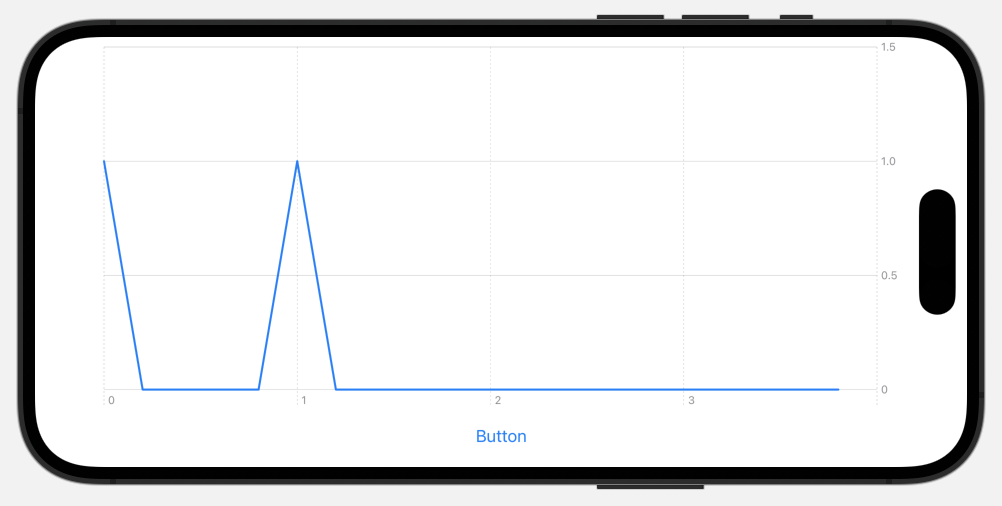
拡大は通常Chartでやるのが良いかもしれませんが、今回はデータそのものをスライスしてみました。以下のコードでデータ範囲を絞ることができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 |
Button("Button"){ // ボタンイベント // 関数を実行してx, y演算結果を取得 let result = wavePoints(dt: 0.01, length: 5) x = result.xArray y = result.yArray // DFTを計算 let dftResult = dft(x, y) let freq = dftResult.0 let amp = dftResult.1 let filteredFreq = freq[..<20] let filteredAmp = amp[..<20] // プロットデータの全削除 data.removeAll() // プロットデータの追加 for i in 0..<filteredFreq.count { data.append(.init(xValue: filteredFreq[i], yValue: filteredAmp[i])) } } |
まとめ
この記事ではPythonで離散フーリエ変換のアルゴリズムを確認した後、Swiftで同様の機能を有するコードを書いてみました。
今回紹介したコードはアルゴリズムの理解を優先したためまだ実用からは少し遠いものとなっていますが、関数や複素数構造体の定義、Chartへ周波数データを渡すといった一連の作業を体験できました。
SwiftにはAccelerateといったライブラリを使うことで高速フーリエ変換ができるらしいので、次回はそのあたりを書いてみようと思います。
DFT計算をiOSでもできるようになりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!