
振動系の運動方程式において復元力項が非線形になった時、その周波数応答関数は特徴的な形を示します。この記事では非線形ばねを有する1自由度の運動方程式を題材に、ハードニング特性やソフトニング特性の周波数応答関数をPythonで解析する方法を紹介します。
こんにちは。wat(@watlablog)です。今回は非線形ばねを持つ振動系の解析から周波数応答関数を計算してみます!
非線形ばねを持つ振動系について
線形ばね
この記事で扱う非線形ばね特性を理解するために、まずは下図に示すような1自由度の振動系を確認します。
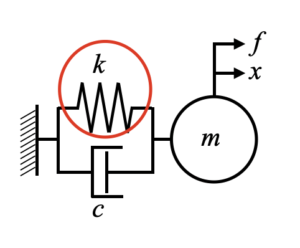
ここで、線形のばね特性を持つ場合は式(1)の運動方程式で振動状態を記述できます。
この辺の解析方法は「Pythonで1自由度減衰系の強制振動シミュレーション」に記載しましたが、解析結果は素直な調和振動となります。
非線形ばね
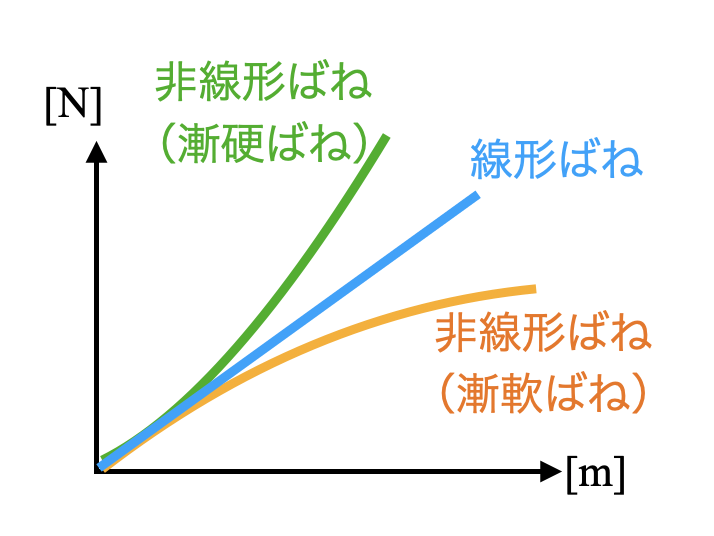
続いて非線形ばねとは下図に示すような、変位に対して発生する復元力が線形ではない特性を示します。
ここで変位の増加によってだんだん硬くなるばねを漸硬ばね、だんだん軟らかくなるばねを漸軟ばねと呼びます。漸硬特性のことをハードニング特性、漸軟特性のことをソフトニング特性と呼んだりもします。
漸硬ばねの例はたくさんあり、材料力学でよく問題となる片持ち梁や両端支持梁、単純なコイルスプリングや板ばね等様々な実際のばねが当てはまります。
実際の金属ばねは無限に伸びることがなく、ある程度変位するとだんだん力をかけても伸びにくくなります(復元力特性に3乗項が出てくる)。
対して漸軟ばねは、変位に対して一度硬くなった後に軟化するようなゴム材料が代表例と思います。また、宇宙機器に見られる柔軟構造物も構造物全体として漸軟特性を持つそうです\(^{[1]}\)(知らなかった!)。
運動方程式
非線形ばねを有する有名な運動方程式として式(2)のDuffing振動子が挙げられます。
この方程式は「PythonでDuffing振動子を解析してアトラクターを見る」で紹介したように、パラメータの取り方によってはカオス振動になり、特徴的なアトラクターを観察できることがわかっています。
機械工学的に式(2)をみれば、変位\(x\)の係数である\(\alpha\)と\(\beta\)が復元力にかかる係数であることがわかります。特に\(\beta\)は変位の3乗にかかる係数であり非線形特性を左右するパラメータです。
\(\beta\)の値が正(+)であれば系は漸硬ばね、負(−)であれば漸軟ばねの特性を示します。
周波数応答関数
非線形ばね特性を持つ振動子の強制振動下における周波数応答関数は特徴的な形になります。
※周波数応答関数については「Pythonで伝達関数!2つの信号の周波数応答関数を計算する方法」をご確認ください。
さらに、加振周波数を低周波数から高周波数に挿引(アップスイープ)する時と高周波数から低周波数に挿引(ダウンスイープ)する時で周波数応答関数が変わります。
漸硬ばねの共振曲線
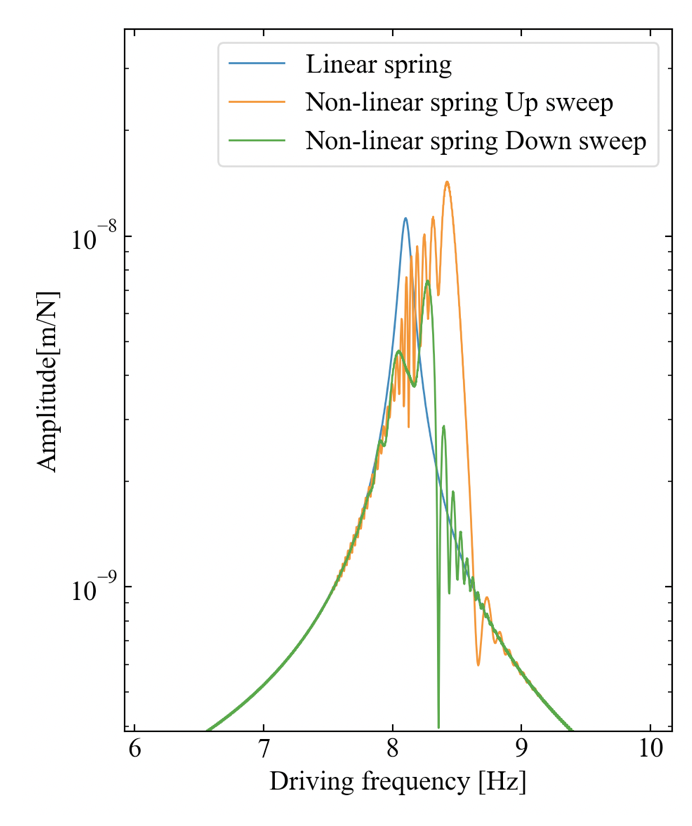
下図に漸硬ばね特性を持つ系の周波数応答関数例を示します。加振周波数を横軸にとり、入出力比の振幅成分ピークが共振を示していることから共振曲線とも呼ばれます。
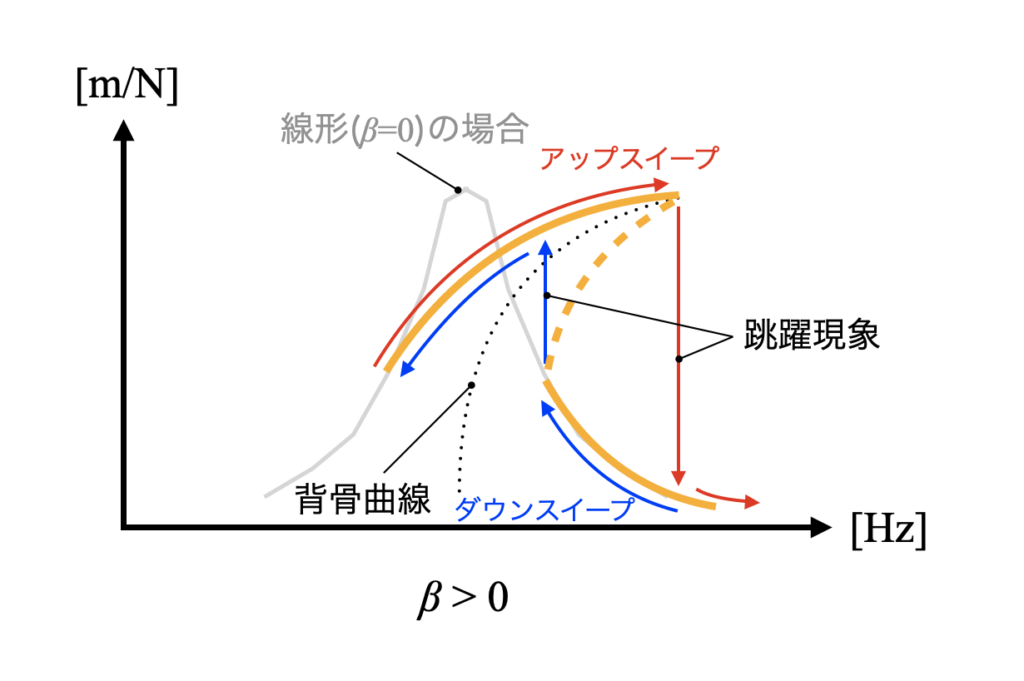
式(2)の\(\beta\)が0の場合、振動系は線形となります。漸硬特性を持つばねの場合、周波数応答関数はピークが高周波数側に傾く形となる特徴を持ちます。
図中黒点線は背骨曲線(Backbone curve)と呼び\(^{[2]}\)、共振曲線の傾きが表現されています。そして非線形ばね特性を持つ共振曲線で見られる重要な現象として、跳躍現象(Jump phenomenon)\(^{[2]}\)が挙げられます。
跳躍現象はアップスイープとダウンスイープの両方で現れ、振幅成分が急激に変化してしまう現象です。
機械構造物の外力周期が変化してこの跳躍現象が起こると、質量を持った物体の振幅が急激に変化するため衝撃的なダメージが構造物に加わることになります。そのため非線形性を持つ製品の強度設計は特に注意しなければいけません。
漸軟ばねの共振曲線
続いて漸軟ばねの共振曲線を以下に示します。漸軟ばねの場合は先ほどの漸硬ばねと左右反転した共振曲線を持ちます。跳躍現象や背骨曲線といった特徴も同様に持ちます。
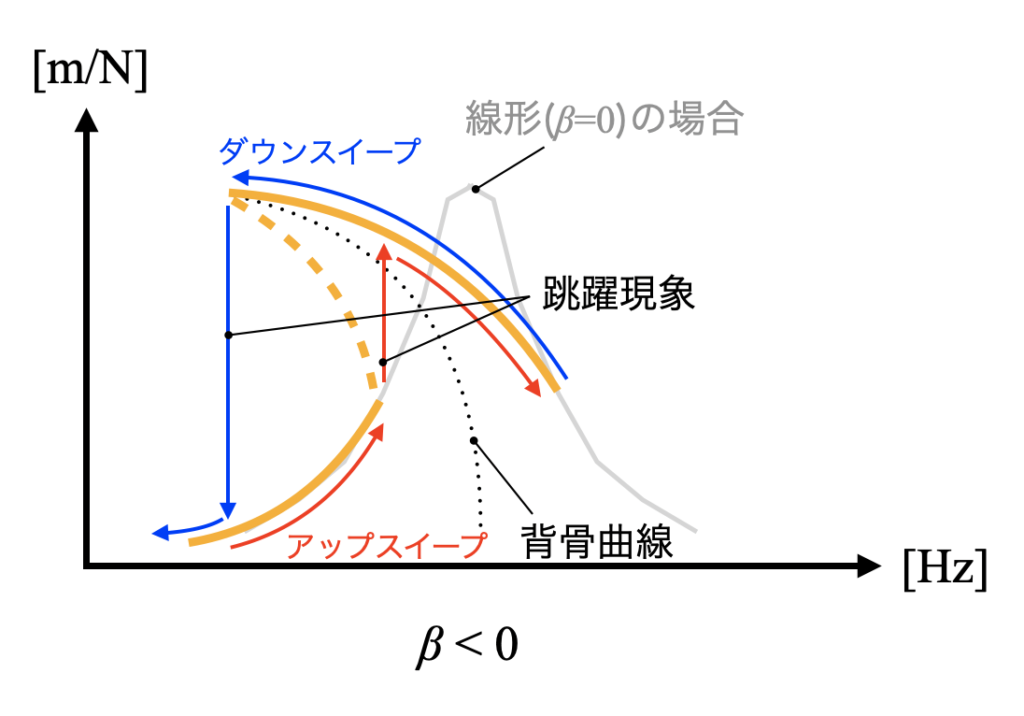
この記事では非線形の運動方程式としてDuffing振動子をモデル化し、Pythonを使って共振曲線をプロットするところまでを扱います。それでは以下より実際にプログラミングを行ってみましょう。
Pythonで非線形ばね特性を持つ振動子の共振曲線を描くコード
動作環境
プログラミングは以下のPython環境で動作確認を行いました。
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| Scipy | 1.4.1 |
| matplotlib | 3.4.3 |
よくある問題
非線形ばねの共振曲線をプロットする場合、運動方程式の外力項にチャープ信号を設定し、過渡応答解析で数値計算するのが一般的だと思います。チャープ信号を使うのは、アップスイープとダウンスイープを表現したいからです。
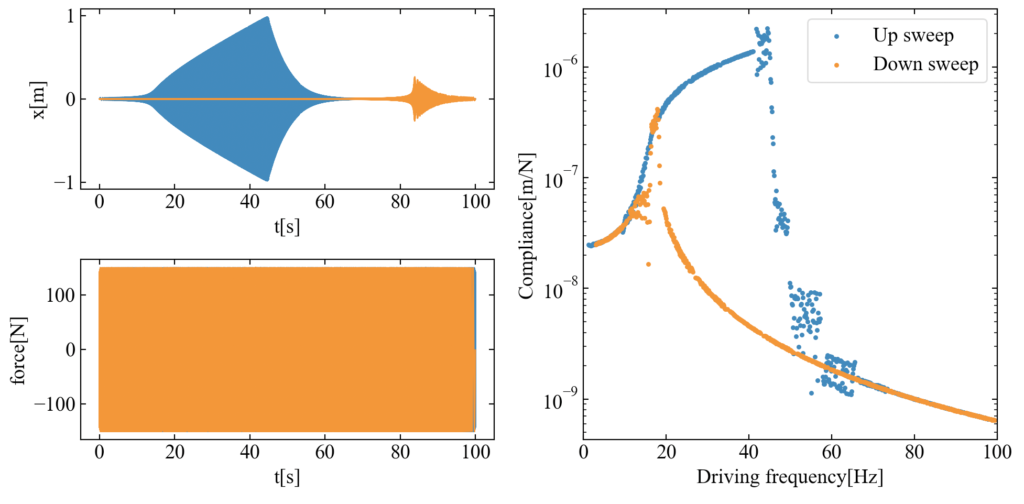
得られた出力信号(変位等)と外力信号を使って周波数応答関数(フーリエ変換で計算)を求めれば良いと思いますが、単純に信号全体をフーリエ変換すると綺麗な共振曲線が得られません。
↓こんな感じ(やってみました)
色々試行錯誤した後述の方法だと綺麗に共振曲線を描けて、跳躍現象も確認できたのですが、なぜこうなるのか…。長時間データをフーリエ変換したことによる周波数分解能の影響か、非線形系は共振部分が不安定なのか…うまい説明がまだできません。
本当はこのような非線形特性を持つ運動方程式の解析は、ハーモニックバランス法というもので解析すると非常に綺麗に共振曲線を得ることができるようですが、まだスキル不足であるためイメージしやすい過渡応答解析でなんとかするという方針です。
コーディング方針
SciPyのodeintで解析する
過渡応答解析は普段自前のRunge-Kutta法で行っていましたが、やはりSciPyのodeintを使った方が明らかに高速だったので今回もodeintを使います。
odeintを使った解析方法は「PythonでDuffing振動子を解析してアトラクターを見る」を参考にしてください。
加振周波数を検出してFRFを計算する
今回はチャープ信号を使って振動モデルを加振させます。チャープ信号は時間の関数で与えられるため、瞬間の時刻を抽出すると加振させている周波数はごく限定的な瞬時周波数のみとなり、それ以外の周波数帯域は加振されません。
非線形特性を持つ周波数応答関数(FRF)は線形の場合と異なり、ホワイトノイズのような加振成分では傾いた共振曲線が得られないことが理由で1ショットフーリエ変換で綺麗な曲線が得られないと考え、今回は加振周波数を検出してFRFを計算する手段をとりました。
アルゴリズムを図解したものがこちら。
一般的な正しいやり方がわからなかったのでとりあえず時間信号をフレーム単位で抽出、加振信号はヒルベルト変換を使って瞬時周波数を計算し、最大周波数と最小周波数を検出してその範囲のFRFのみをデータとする方法をとりました。
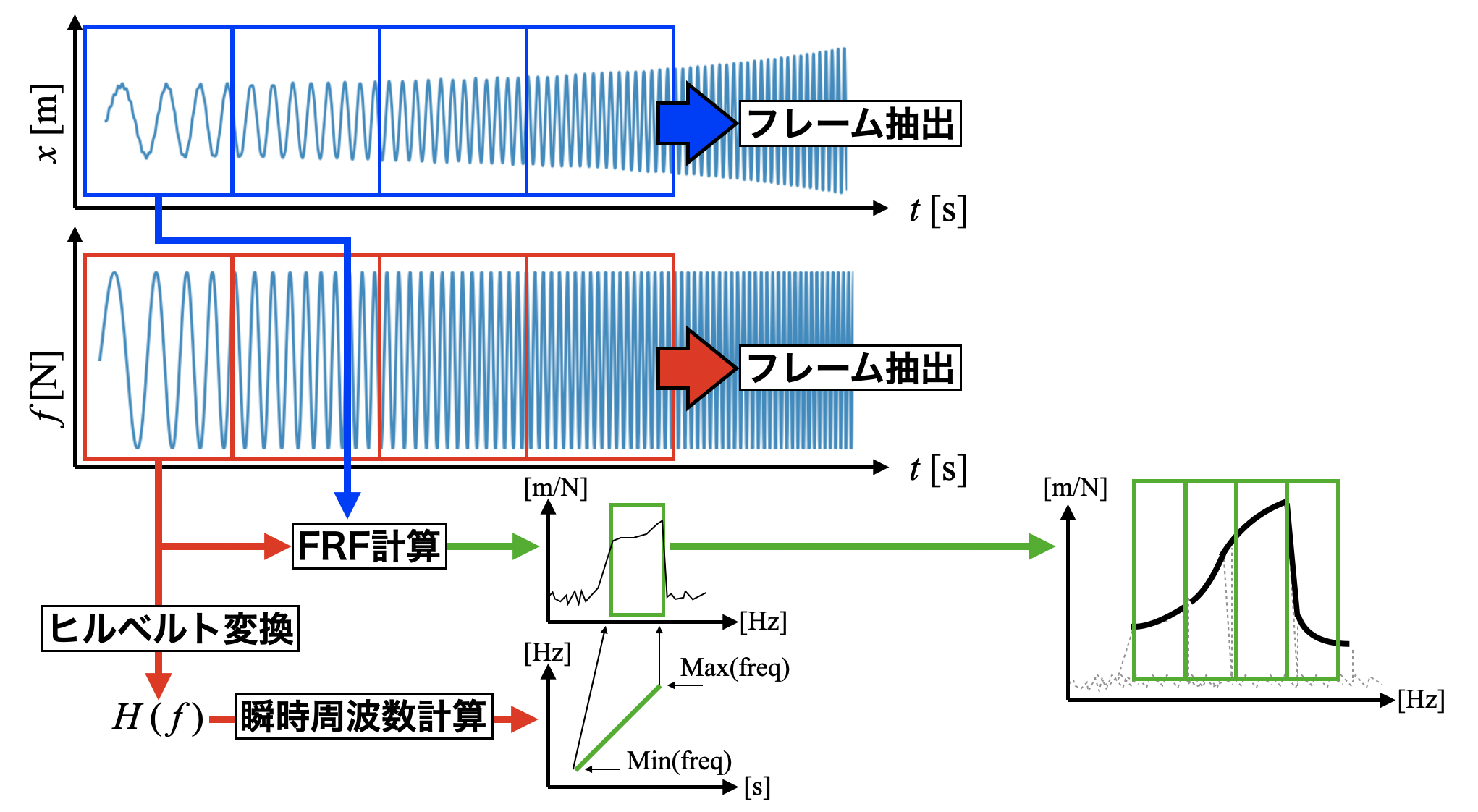
…ここはプログラムを見てもらった方がわかりやすいかも。この辺は説明が面倒なのであまり説明の需要がなさそうなのでコードをご覧ください。
チャープ信号は自前の式で与える
チャープ信号(サインスイープ信号)はこれまでSciPyのsignalライブラリを使って生成していましたが、odeintの中で使うためには時間の関数として求められる形にしておく必要があります。
そのため式(3)と式(4)でチャープ信号を定義しました\(^{[3]}\)。
漸硬特性の周波数応答関数を求めるコード例
以下が先ほどのアルゴリズムをPythonコードで表現した結果です。正しいやり方かはやはり疑問が残りますが、とりあえずコピペで動くはずです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 |
import numpy as np from scipy import fftpack from matplotlib import pyplot as plt from scipy.integrate import odeint def f(var, t, alpha, beta, delta, gamma, f0, k): ''' Duffing oscillator ''' force = gamma * np.sin(2 * np.pi * (f0 * t + (k / 2) * t ** 2)) v = var[1] a = - alpha * var[0] - beta * var[0] ** 3 - delta * var[1] + force return np.array([v, a]) def plot(t, x, force, freq, amp, label): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('force[N]') ax3.set_xlabel('Driving frequency[Hz]') ax3.set_ylabel('Compliance[m/N]') # スケールの設定をする。 ax3.set_xlim(0, 100) ax3.set_yscale('log') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 for i in range(len(x)): ax1.plot(t, x[i], label='Displacement', lw=1) ax2.plot(t, force[i], label='Force', lw=1) ax3.scatter(freq[i], amp[i], label=label[i], s=5) # レイアウト設定 fig.tight_layout() ax3.legend() # グラフを表示する。 plt.show() plt.close() def frf(input_array, output_array, samplerate): ''' 周波数応答関数(FRF) ''' freq_array = [] amp_array = [] for i in range(len(input_array)): # ヒルベルト変換で瞬時周波数を計算 instantaneous_frequency = hilbert(input_array[i], 1 / samplerate) # 5%端部を除外(ヒルベルト変換が安定している部分を確実に抽出するため) index_remove = int(len(instantaneous_frequency) * 0.05) instantaneous_frequency = instantaneous_frequency[index_remove:len(instantaneous_frequency) - index_remove] # 瞬時周波数の最大と最小を計算 freq_min = np.min(instantaneous_frequency) freq_max = np.max(instantaneous_frequency) # 入出力信号のフーリエ変換 fft_i = fftpack.fft(input_array[i]) fft_o = fftpack.fft(output_array[i]) # FRFを計算 h_io = (fft_o * fft_i.conjugate()) / (fft_i * fft_i.conjugate()) amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) amp = amp / (len(input_array[i]) / 2) # チャープ信号の周波数範囲のみをデータとする freq = np.linspace(0, samplerate, len(amp)) df = freq[1] freq_region = freq[int(freq_min / df):int(freq_max / df)] amp_region = amp[int(freq_min / df):int(freq_max / df)] freq_array = np.concatenate([freq_array, freq_region]) amp_array = np.concatenate([amp_array, amp_region]) return freq_array, amp_array def ov(data, samplerate, Fs, overlap): ''' 時間波形のオーバーラップ処理 ''' # 全データ長とフレーム周期 Ts = len(data) / samplerate Fc = Fs / samplerate # オーバーラップ時のフレームずらし幅 x_ol = Fs * (1 - (overlap / 100)) # 抽出するフレーム数(平均化に使うデータ個数) N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # データ抽出 array = [] for i in range(N_ave): ps = int(x_ol * i) array.append(data[ps:ps + Fs:1]) return array, N_ave def hilbert(yt, dt): '''ヒルベルト変換''' # フーリエ変換 spectrum = fftpack.fft(yt) # 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(spectrum) / 2)) spectrum[int(len(spectrum) / 2):len(spectrum)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する spectrum *= 2 # 実部と虚部から瞬時振幅と瞬時位相を計算する zt = fftpack.ifft(spectrum) re = zt.real im = zt.imag # 瞬時振幅 instantaneous_amp = np.sqrt(re ** 2 + im ** 2) # 瞬時位相とアンラップ処理 instantaneous_phase = np.arctan2(im, re) instantaneous_phase = np.unwrap(instantaneous_phase) # 瞬時周波数(位相角の微分と時間刻み影響を考慮) instantaneous_frequency = ((1 / dt) / (2 * np.pi)) * np.gradient(instantaneous_phase) return instantaneous_frequency if __name__ == '__main__': ''' メイン処理 ''' # 解析時間 t_min = 0 t_max = 100 dt = 1e-3 t = np.arange(t_min, t_max, dt) # ダフィング振動子のパラメータ alpha = 10000.0 beta = 100000.0 delta = 0.5 gamma = 150.0 # 外力パラメータ(アップスイープとダウンスイープ) force_set = [[1.0, 100.0], [100.0, 1.0]] x_list = [] force_list = [] freq_array_list = [] amp_array_list = [] for i in range(len(force_set)): # チャープ信号式を計算 f0 = force_set[i][0] f1 = force_set[i][1] k = (f1 - f0) / t_max force = gamma * np.sin(2 * np.pi * (f0 * t + (k / 2) * t ** 2)) force_list.append(force) # 初期条件 var = [0.0, 0.0] # 微分方程式の近似解法(過渡応答) var = odeint(f, var, t, args=(alpha, beta, delta, gamma, f0, k)) x, v = var.T[0], var.T[1] # オーバーラップ処理 Fs = 8192 input_array, input_N_ave = ov(force, 1 / dt, Fs, 0) output_array, output_N_ave = ov(x, 1 / dt, Fs, 0) # 周波数応答関数を計算 freq_array, amp_array = frf(input_array, output_array, 1 / t[1]) x_list.append(x) freq_array_list.append(freq_array) amp_array_list.append(amp_array) # プロット plot(t, x_list, force_list, freq_array_list, amp_array_list, ['Up sweep', 'Down sweep']) |
こちらが結果。プログラムを実行するとアップスイープとダウンスイープのシミュレーション結果が2つ分走り、重ね描きプロットされます。漸硬ばね特性の特徴を周波数応答関数で見ることができました。
漸軟特性の周波数応答関数を求めるコード例
続いて漸軟ばねの特性を持つ振動子のシミュレーションコード例を紹介します。
といっても、先ほど紹介した全体コードの内、パラメータ設定の部分のみ以下の数値に更新するだけです。
|
1 2 3 4 5 |
# ダフィング振動子のパラメータ alpha = 50000.0 beta = -35000.0 delta = 0.9 gamma = 150.0 |
漸軟特性は低周波数側に傾くので、先ほどのパラメータだと左側の余白が足りず、固有振動数を高周波数側に少しずらしてみました。
下図が結果です。低周波側に傾く共振曲線を観察することができました。
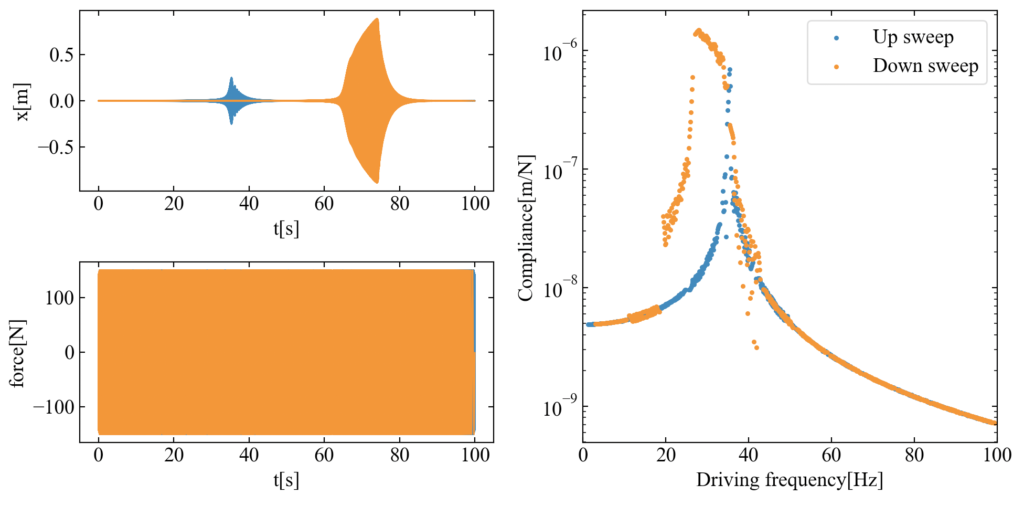
まとめ
今回は1自由度を例に非線形ばね特性を持つ振動系の周波数応答関数をPythonで計算しました。
過渡応答の数値計算で綺麗に共振曲線を得るために色々工夫してみましたが、実際こんなことが必要だったのかはまだよくわかりません。個人ブログなので、やってみたことを記録するという意味合いで記事を作成しました。
とはいえ物理的に重要な漸硬ばね特性や漸軟ばね特性、跳躍現象等がシミュレーションで観察できたので第一歩なのではないでしょうか。
ただ、素直にハーモニックバランス法を覚えた方が良いのかもとは思いました。
→GitHub\(^{[4]}\)やPyPI\(^{[5]}\)にMousaiというライブラリがありました。
こんなものまでパッケージにしている人がいるとは…あとでやってみよう。
https://josephcslater.github.io/mousai/index.html#
https://pypi.org/project/mousai/
非線形振動は周波数領域で見ても時間領域で見ても面白い現象が山ほどあるので、今後も地道に紹介していけたらと思います。
参考文献
[1]:工藤 進 et al., 間欠外力によるダフィング系の振動低減化, 日本機械学会[No07−13]第10回「運動と振動の制御」シンポジウム講演論文集, 2007, pp162
[2]:日本機械学会, JSMEテキストシリーズ 振動学, 丸善出版株式会社, 2018(初版第8刷), pp109
[3]:Wikipedia チャープ信号
[4]:Mousai: A Set of Harmonic Balance Solvers, https://josephcslater.github.io/mousai/index.html#
[5]:Mousai:https://pypi.org/project/mousai/
非線形分野は解析が難しいけど、結果は非常に面白い!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!