
Duffing振動子は非線形の2階常微分方程式です。この方程式をある特定のパラメータ下で解析すると特徴的な模様のアトラクターを観察できます。ここではDuffing振動子の概要と、Pythonによる計算方法を紹介し、自分の手でアトラクターを描くまでを目標とします。
こんにちは。wat(@watlablog)です。ここではDuffing振動子の解析から特徴的なアトラクターを可視化してみます!
Duffing振動子の概要
Duffing振動子の方程式
Duffing振動子(Duffing oscillator)は式(1)で表される2階の常微分方程式です。
ここで\(\delta\)は\(\dot{x}\)(速度)にかかり振動子の減衰を表し、\(\alpha\)や\(\beta\)は\(x\)にかかり剛性を表すパラメータです。
特に\(\beta\)がかかっている\(x^{3}\)項は線形でないため、\(\beta\)の数値によって方程式は非線形特性を持つようになります。
方程式の右辺は強制振動における外力を示し、\(\gamma\)が外力の振幅、\(\omega\)が角振動数、\(\phi\)が位相を意味し時間\(t\)で振動します。
Duffing振動子については以下のScholarpediaのページが一番わかりやすいと思いました。今回はこのページの最初に載っている動画をPythonで作ってみます。
http://www.scholarpedia.org/article/Duffing_oscillator
アトラクターの周期変化を観察するコード
Duffing方程式を解析するコード
先ほどのリンク先によると、式(1)のパラメータを以下にセットして\(\frac{2\pi}{\omega}\)の周期で出力を観察することで、特徴的なアトラクターを見ることができるそうです。
- \(\alpha\) = -1.0
- \(\beta\) = 1.0
- \(\delta\) = 0.2
- \(\gamma\) = 0.3
- \(\omega\) = 1.0
今回はSciPyのodeintを使ってみました。これまで当ブログでは自作のRunge-Kutta法を使っていましたが、やはり計算速度が段違いであることに気付きました。非線形振動を計算する場合計算速度は重要です。ここは素直に巨人の肩に乗ってみましょう。
公式ドキュメントを以下に示します。
SciPy odeint:https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.odeint.html
それでは、基本の解析コードを紹介します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
import numpy as np from matplotlib import pyplot as plt from scipy.integrate import odeint def f(var, t, alpha, beta, delta, gamma, omega, phi): ''' Duffing oscillator ''' v = var[1] a = - alpha * var[0] - beta * var[0] ** 3 - delta * var[1] + gamma * np.cos(omega * t + phi) return np.array([v, a]) def plot(t, x, v): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('v[m/s]') ax3.set_xlabel('x[m]') ax3.set_ylabel('v[m/s]') # スケールの設定をする。 ax1.set_ylim(-1.5, 1.5) ax2.set_ylim(-1.5, 1.5) ax3.set_xlim(-1.5, 1.5) ax3.set_ylim(-1.5, 1.5) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, v, label='Velocity', lw=1, color='red') ax3.scatter(x, v, label='Phase plane', lw=1, color='red', s=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' # ダフィング振動子のパラメータ alpha = -1.0 beta = 1.0 delta = 0.2 gamma = 0.3 omega = 1.0 phi = 0 # 解析時間 t = np.arange(0, 10000, (2 * np.pi) / omega) # 初期条件 var = [0.0, 0.0] # 微分方程式の近似解法(過渡応答) var = odeint(f, var, t, args=(alpha, beta, delta, gamma, omega, phi)) x, v = var.T[0], var.T[1] # プロット plot(t, x, v) |
関数f()でDuffing振動子を定義しています。メイン処理の部分でパラメータをセットしodeintを使っていますが、このコードはそれほど長くないのでコード内コメントを見て頂ければ内容がわかると思います。
コードを実行すると以下の結果を得ます。時間波形として変位と速度をプロットしていますが、変位と速度(変位の微分)で構成される位相平面(Phase plane)もプロットしています。この位相平面はポアンカレ切断面(Poincaré section)、またはポアンカレ写像図(Poincaré map)とも呼ばれます。
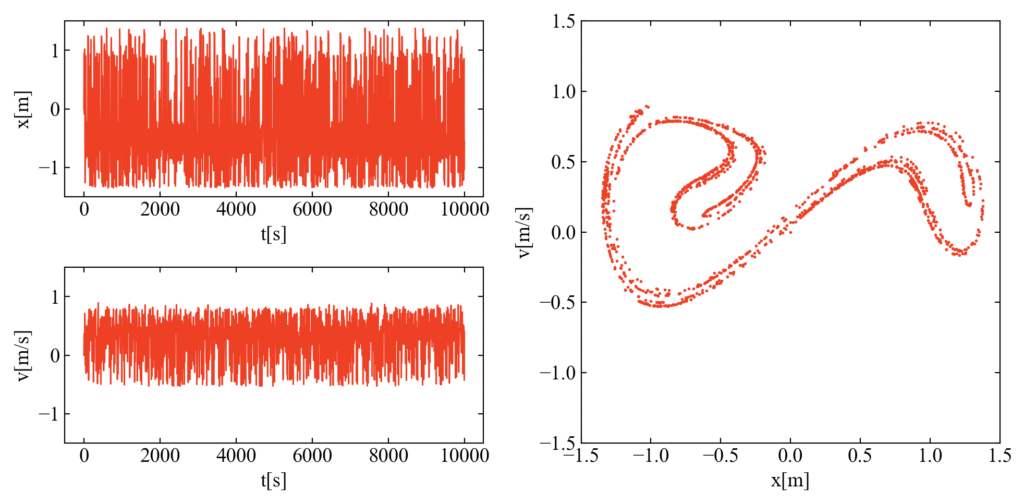
特徴的なプロットが確認されました!
ポアンカレ写像図のアニメーションを作成するコード
次にDuffing振動子解析時の位相\(\phi\)を少しずつずらしながら\(2\pi\)まで計算し、結果をアニメーションにしてみます。これが先ほど紹介したScholarpediaのページに載っていた動画となります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
import numpy as np from matplotlib import pyplot as plt from scipy.integrate import odeint from PIL import Image import os import glob def f(var, t, alpha, beta, delta, gamma, omega, phi): ''' Duffing方程式 ''' v = var[1] a = - alpha * var[0] - beta * var[0] ** 3 - delta * var[1] + gamma * np.cos(omega * t + phi) return np.array([v, a]) def plot(t, x, v, dir_name): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('v[m/s]') ax3.set_xlabel('x[m]') ax3.set_ylabel('v[m/s]') # スケールの設定をする。 ax1.set_ylim(-1.5, 1.5) ax2.set_ylim(-1.5, 1.5) ax3.set_xlim(-1.5, 1.5) ax3.set_ylim(-1.5, 1.5) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, v, label='Velocity', lw=1, color='red') ax3.scatter(x, v, label='Phase plane', lw=1, color='red', s=1) # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 if os.path.exists(dir_name): pass else: os.mkdir(dir_name) # 画像保存パスを準備 path = os.path.join(*[dir_name, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 # plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルのフルパスからファイル名と拡張子を抽出 imgs = [] for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0) return if __name__ == '__main__': ''' メイン処理 ''' # ダフィング振動子のパラメータ alpha = -1.0 beta = 1.0 delta = 0.2 gamma = 0.3 omega = 1.0 # 位相リスト n = 50 phi_list = np.arange(0, 2 * np.pi, 2 * np.pi / n) # 解析時間 t = np.arange(0, 5000, 2 * np.pi / omega) # 初期条件 var = [0.0, 0.0] # 画像保存フォルダ dir_name = 'duffing' # 位相毎にプロットを画像保存しアトラクターを可視化する for i in range(len(phi_list)): print('Iteration=', i) # 位相 phi = phi_list[i] # 微分方程式の近似解法(過渡応答) var = odeint(f, var, t, args=(alpha, beta, delta, gamma, omega, phi)) x, v = var.T[0], var.T[1] # 初期値を更新 var = x[-1], v[-1] # プロット plot(t, x, v, dir_name) create_gif(dir_name, 'duffing-phase-plot.gif') |
以下の動画が実行結果として得られるgifファイルです。
\(\frac{2\pi}{\omega}\)の周期で抽出した時間波形の見た目は完全なランダムなように見えますが、位相平面を見ると全体的にはある範囲にまとまり、さらにその形状はなんとも不思議な形が変形を伴って周期的な挙動をしています。
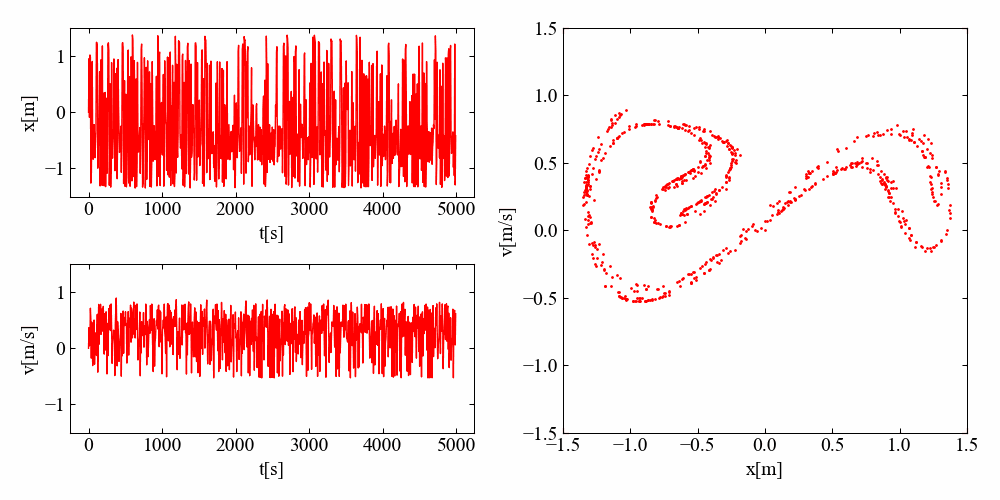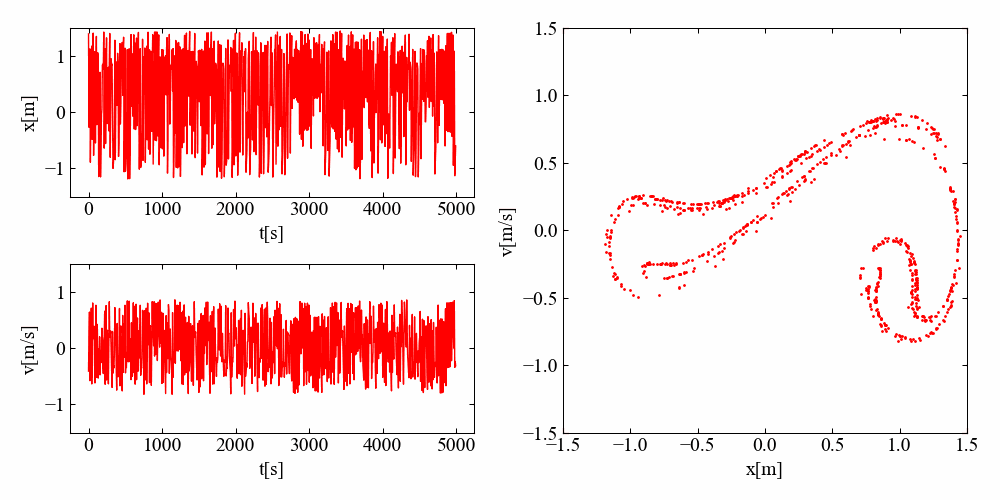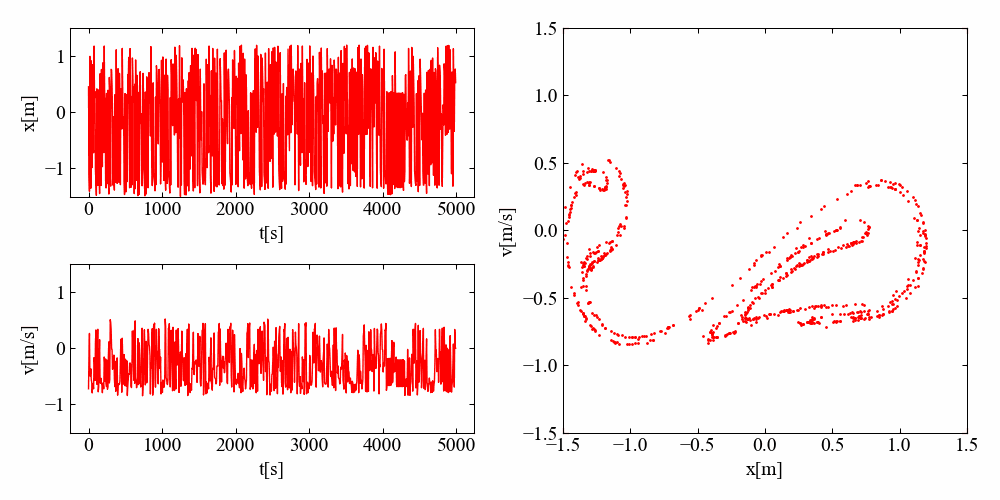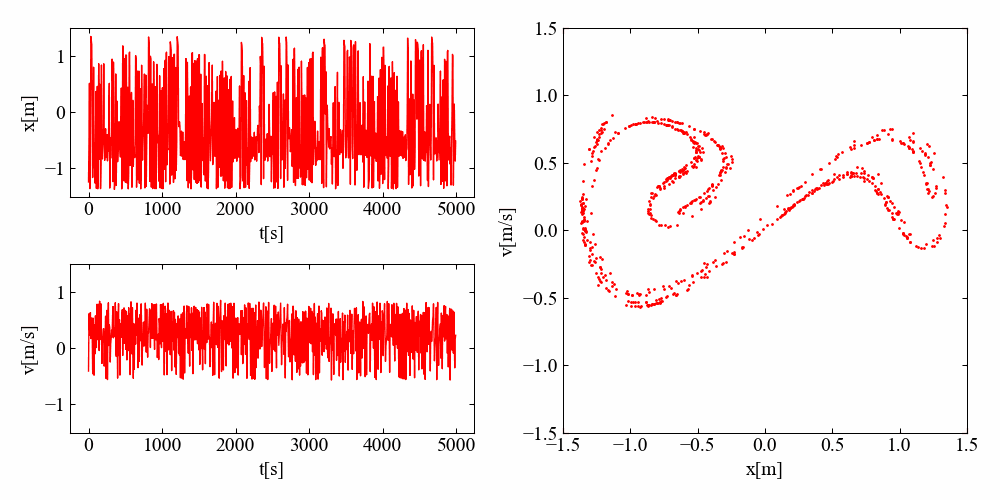
不思議ですね…!計算結果だけではなく、これを見る僕もアトラクターの影響を受けているようです。
ジャパニーズ・アトラクターも見てみる
ジャパニーズ・アトラクター(Japanese Attractor)というのは、日本人の上田睆亮氏が発見したアトラクターで、有名なローレンツ・アトラクターとほぼ同時期に発見された\(^{[1]}\)とのことです。
上田の名前をとってウエダ・アトラクターと呼ばれることもあります。このウエダ・アトラクターは非線形インダクタンスを持つ直列共振回路の回路方程式から導出されたもので、式(1)のDuffing振動子を以下のパラメータで解析すると可視化可能です。
- \(\alpha\) = 0.0
- \(\beta\) = 1.0
- \(\delta\) = 0.1
- \(\gamma\) = 12.0
- \(\omega\) = 1.0
このアトラクターは位相により広範囲に可動するので、初期値[0, 0]では発散してしまう場合があります。そのため位相0時のPythonコードは以下のようにパラメータと共に初期値を設定しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# ダフィング振動子のパラメータ alpha = 0.0 beta = 1.0 delta = 0.1 gamma = 12.0 omega = 1.0 phi = 0.0 # 解析時間 t = np.arange(0, 10000, (2 * np.pi) / omega) # 初期条件 var = [3.0, 0.1] |
静止画として可視化した結果がこちら。この結果もすごく不思議な形をしていますね。
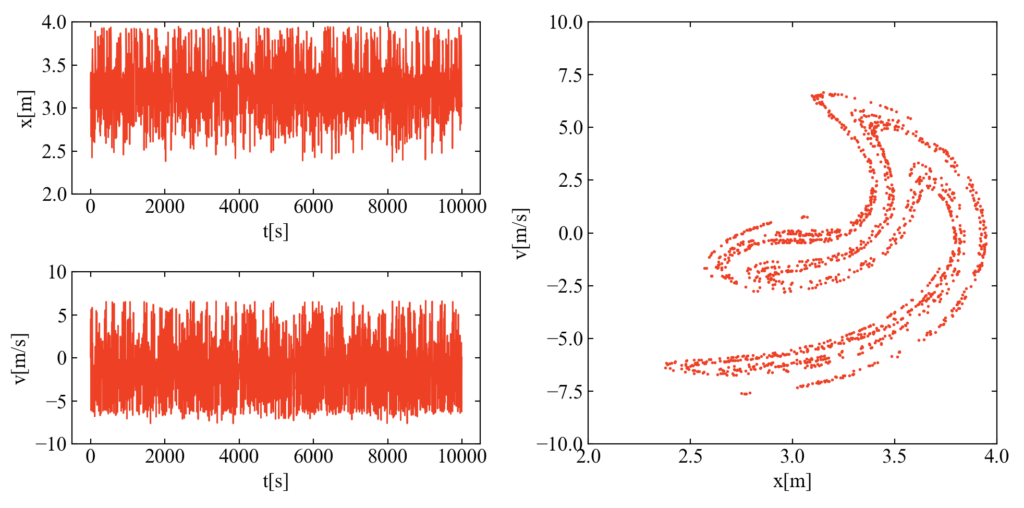
動画を作成するコードはこちら。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 |
import numpy as np from matplotlib import pyplot as plt from scipy.integrate import odeint from PIL import Image import os import glob def f(var, t, alpha, beta, delta, gamma, omega, phi): ''' Duffing方程式 ''' v = var[1] a = - alpha * var[0] - beta * var[0] ** 3 - delta * var[1] + gamma * np.cos(omega * t + phi) return np.array([v, a]) def plot(t, x, v, dir_name): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(10, 5)) ax1 = fig.add_subplot(221) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(223) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(122) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x[m]') ax2.set_xlabel('t[s]') ax2.set_ylabel('v[m/s]') ax3.set_xlabel('x[m]') ax3.set_ylabel('v[m/s]') # スケールの設定をする。 ax1.set_ylim(-5.0, 5.0) ax2.set_ylim(-10.0, 10.0) ax3.set_xlim(-5.0, 5.0) ax3.set_ylim(-10.0, 10.0) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='Displacement', lw=1, color='red') ax2.plot(t, v, label='Velocity', lw=1, color='red') ax3.scatter(x, v, label='Phase plane', lw=1, color='red', s=1) # レイアウト設定 fig.tight_layout() # 画像を保存する。 # dirフォルダが無い時に新規作成 if os.path.exists(dir_name): pass else: os.mkdir(dir_name) # 画像保存パスを準備 path = os.path.join(*[dir_name, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 # plt.show() plt.close() def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルのフルパスからファイル名と拡張子を抽出 imgs = [] for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0) return if __name__ == '__main__': ''' メイン処理 ''' # ダフィング振動子のパラメータ alpha = 0.0 beta = 1.0 delta = 0.1 gamma = 12.0 omega = 1.0 # 位相リスト n = 50 phi_list = np.arange(0, 2 * np.pi, 2 * np.pi / n) # 解析時間 t = np.arange(0, 5000, 2 * np.pi / omega) # 初期条件 var = [3.0, 0.1] # 画像保存フォルダ dir_name = 'duffing' # 位相毎にプロットを画像保存しアトラクターを可視化する for i in range(len(phi_list)): print('Iteration=', i) # 位相 phi = phi_list[i] # 微分方程式の近似解法(過渡応答) var = odeint(f, var, t, args=(alpha, beta, delta, gamma, omega, phi)) x, v = var.T[0], var.T[1] # 初期値を更新 var = x[-1], v[-1] # プロット plot(t, x, v, dir_name) create_gif(dir_name, 'duffing-phase-plot.gif') |
そして結果がこちら。ジャパニーズ・アトラクターも位相を進めていくと時計回りに回転しているような挙動をしていますが、バウンドする回数に違いがあるみたいです。これが何を意味するのかはさっぱりわかりませんが、見ていて飽きない不思議な結果ですね…。
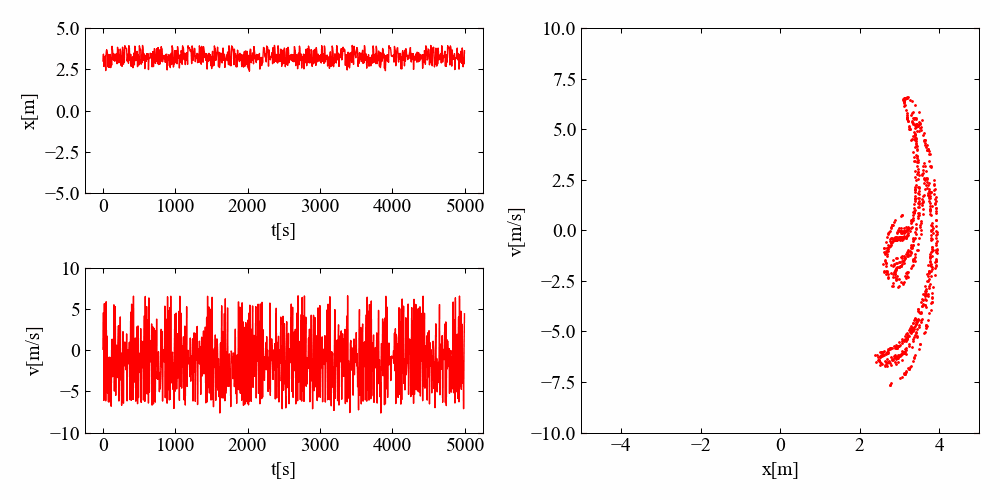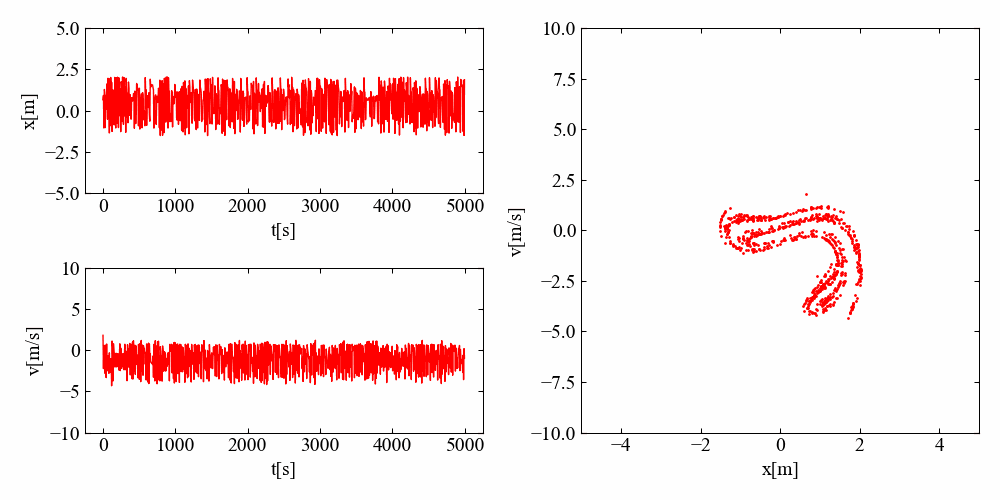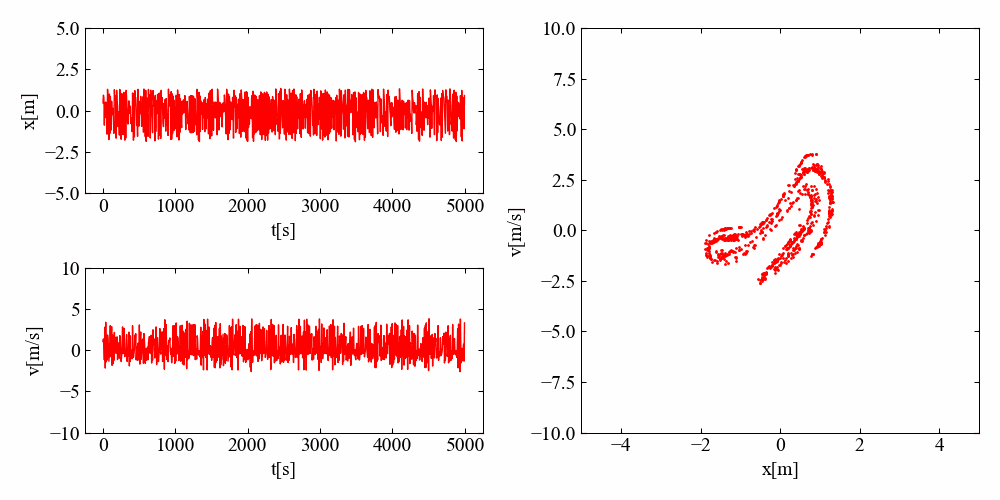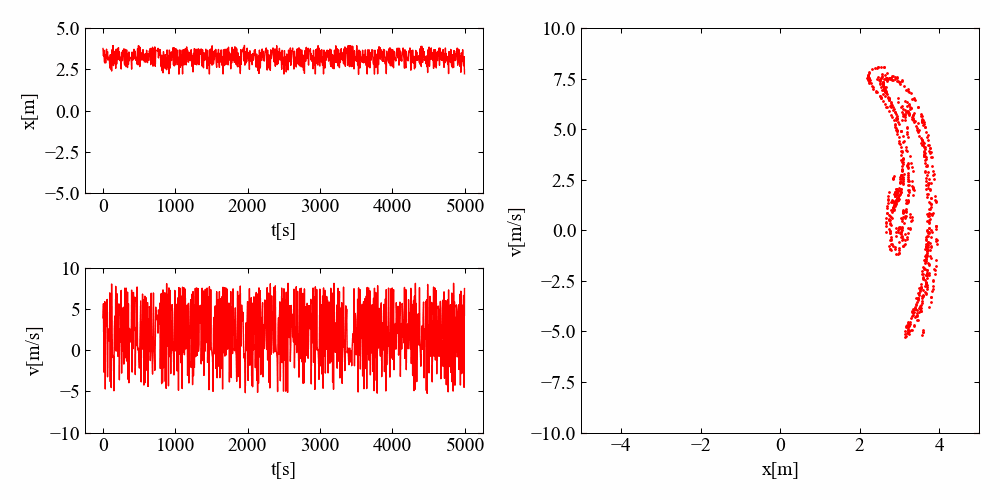
まとめ
この記事はここまで。
Duffing振動子は3乗項が非線形ばねの特性を持ち工学的に面白い周波数応答関数を持つのですが、それは次の記事で扱います。
今回はDuffing振動子の魅力として、アトラクターの可視化のみを扱いました。ここで紹介した形以外もたくさん発見されているようなので、是非皆さんのお手持ちのPCでカオスを体験してみてください。
参考文献
[1]:逢沢明, カオスの縁から<複雑適応系>を探検する偏 複雑系はいつも複雑, 現代書館, 1997, pp174アトラクターの魅力にすっかりはまりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!