ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
固有値と固有ベクトルを学んだら対角化を学びましょう。対角化は行列の計算を容易にさせるメリットがあります。ここでは対角化の概要と、Pythonによる計算の例を紹介します。
こんにちは。wat(@watlablog)です。
線形代数の学習を始めて固有値の計算を習得したら、是非行列の対角化も学びましょう！ここでは対角化の方法とPythonコードを紹介します！
僕は線形代数の勉強を「中井悦司, 技術者のための線形代数学, 翔泳社※Amazon」でしています。書籍ではプログラミングについては触れていませんが、ここではPythonによるコーディングにフォーカスして学んだ事の実践を行います。
線形代数学の内容について、より理解を深めたい方は本書の購入をすることで、当ブログで紹介するPythonコードの意味がよくわかるようになると思います。
当ブログでは、基本的に難しい説明は面倒なのでできるだけしないようにし、結果がPythonで簡単に得られることを優先するという方針で進めます！
ちなみに、今回はP40からの内容と関係しています！
行列の対角化の概要
対角行列とは？どんなメリットがあるの？
対角行列とは、以下の行列Aのように対角線上にしか値(この場合は\(\lambda\))が入っておらず、その他は全て0という行列のことを言います。
\[
\mathbf{A}=
\begin{bmatrix}
\lambda_{1} &0 &0 \\
0 &\lambda_{2} &0 \\
0 &0 &\lambda_{3}
\end{bmatrix}
\]
ちなみに、書籍によってはdiagonalを使って以下のように表記することもあります。
\[\mathbf{A}=\mathrm{diagonal}\left[\lambda_{1},\lambda_{2}, \lambda_{3} \right ]\]
この対角行列はとにかく計算が楽というメリットがあります。
例えば行列Aのn乗をみてみましょう。行列Aをn乗するということは、A×A×…とn回計算するということを意味します。
通常の数値ならいざ知らず、行列の乗算はかける順序が決まっているのでプログラムでも使わないとやってられませんよね？
でも対角行列のn乗であれば以下のように簡単に計算することができますね！
\[
\mathbf{A}^{n}= \begin{bmatrix}
\lambda_{1}^{n} &0 &0 \\
0 &\lambda_{2}^{n} &0 \\
0 &0 &\lambda_{3}^{n}
\end{bmatrix}
\]
これなら1億乗だって苦じゃないぞ！
いや、流石に1億乗はやりたくありませんが、対角化された行列は計算が楽なんです。
他にも物理的、工学的な計算を行う際にも対角化は意味を持ちます。
対角化できる行列とは？
対角化は大変便利ですので、この世の全ての行列を対角化してしまえば良いではないか、という極論を思い立ったあなた！それはできません！
行列を対角化させるにはn次正方行列であればn次の固有ベクトルが必要です。その固有ベクトルを使った行列で対角化を行いますが、対角化に使う行列のことを変換行列とも呼びます。
固有ベクトルについては前回の記事、「Pythonで線形代数！固有値と固有ベクトルを求める」で手計算も交えながら説明しましたので、そちらを参照頂ければと思います。
そしてこの固有ベクトルですが、他にも1次独立である必要があります。
1次独立の対義語は1次従属ですが、大学受験勉強等でベクトルをやっていない人のために少し説明をしておきます。
実は僕も社会人になるまでこの言葉は知りませんでした！（勉強不足でしたね）
イメージを掴むために、まずは2次元平面上のベクトルの組について見てみましょう。
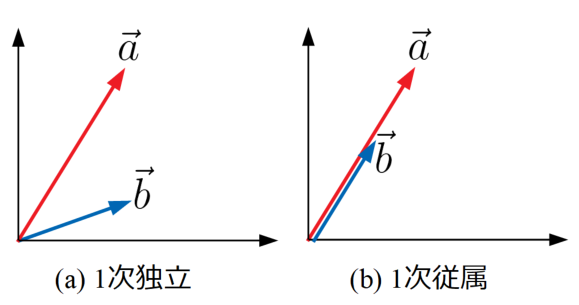
以下の図は二つのベクトル\(\vec{a}\)と\(\vec{b}\)を示していますが、(a)は二つのベクトルは0でなく、平行でもありません。このようなベクトルを1次独立と呼びます。
一方、(b)は0ではありませんが、平行です。この場合は1次従属と呼びます。
今後ブログ内で対角化を行う時に、もし対角化できない行列を扱う時が来たらまた説明するかも知れませんが、やはり数学は専門書を読むに限ります。
この辺の話を数学的にもっとしっかりと理解したい方は、是非「中井悦司, 技術者のための線形代数学, 翔泳社※Amazon」のP15 を参照してみて下さい。僕は数学の専門家ではないのであまり深い話はしません（できません！）。
色々理由の説明や証明はしませんが、ここでは行列の対角化には1次独立の固有ベクトルが必要という程度の知識で構いません。
ジョルダンの標準形を使えば？とかを思う人もいるかも知れませんが、僕がまだ勉強していないのでここでは取り扱いません！
対角化の方法
それでは対角化の方法ですが、n次正方行列の固有ベクトルがn個あったとし、それをPという行列にまとめたものを変換行列として使います。
$$\mathbf{P}= \left [ x_{1},x_{2,}\cdots ,x_{n} \right ]$$
そして、行列Aにこの変換行列Pの逆行列を前からかけ、さらに後ろからは逆行列にしていないPをかけると、対角行列Dが求まります。
$$\mathbf{D}= \mathbf{P}^{-1}\mathbf{A}\mathbf{P}$$
しかも、対角行列の中身は対角線上に行列Aの固有値が順番に並ぶという特徴もあります。
\[
\mathbf{D}= \begin{bmatrix}
\lambda_{1} &0 &\cdots &0 \\
0 &\lambda_{2} &0 &0 \\
\vdots &0 &\ddots &\vdots \\
0 &\cdots &0 &\lambda_{n}
\end{bmatrix}
\]
これ、地味に感動モノ。
では、お待たせしました。ここからPythonによる行列の対角化コードを紹介します！
Pythonによる対角化のコード
Pythonの線形代数プログラミングあるあるですが、行列の対角化は一瞬で終わります。今回は固有値と固有ベクトルも求めるので、「Pythonで線形代数！固有値と固有ベクトルを求める」と同じ例題行列を使っています。
以下のコードの「D＝」の部分が対角化計算です。変換行列を使って行列の積を計算していますが、np.dotを使っているのは、こうしないと行列としての積が計算されず、単なる対応要素の積になってしまうからです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np # 例題の行列 A = np.array([[3, 0], [1, 2]]) # 固有値と固有ベクトルを求める。 eig, P = np.linalg.eig(A) print(eig) print(P) # 対角化 D = np.dot(np.dot(np.linalg.inv(P), A), P) print(D) |
Python3.9以降を使っている人でしたら内積の計算に「@」が使ええます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import numpy as np # 例題の行列 A = np.array([[3, 0], [1, 2]]) # 固有値と固有ベクトルを求める。 eig, P = np.linalg.eig(A) print(eig) print(P) # 対角化 D = np.linalg.inv(P) @ A @ P print(D) |
プログラムを実行すると、以下の結果が得られます。対角行列の数値が先に求めた固有値になっていることを確認できれば終了です！
|
1 2 3 4 5 6 7 8 9 10 |
# 固有値 [2. 3.] # 固有ベクトル [[0. 0.70710678] [1. 0.70710678]] #対角行列D [[2. 0.] [0. 3.]] |
まとめ
固有値と固有ベクトルを求めた後は、対角化までセットで学ぶことがオススメです。
対角化行列とは、行列内の対角線上数値以外は全て0という特殊な行列です。この行列はn乗の計算が非常に楽にできる計算上のメリットや、対角成分が全て固有値になるという特徴を持つことを学びました。
但し、世の中全ての行列が対角化できるわけではないということにも触れました。
対角化の計算もPythonで機械的にできそうだね！線形代数に詳しくなれば技術者としてのレベルが上がるはず！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
D = np.dot(np.dot(np.linalg.inv(P), A), P)
は
D = np.linalg.inv(P) @ A @ P
の方が可読性が高いと思います。
tkoyama010さん、コメントありがとうございます！
この記事を書いた時は古いバージョンだったようですね。
今は@を多用しています。
確かPython3.9から使えたような気がします。