
連立方程式を反復法で解く方法として、直列ではヤコビ法より計算が速く終わるというガウス・ザイデル法を学びます。ここではガウス・ザイデル法がなぜ効率的なのかを式を用いて解説し、Pythonで実装しながら理解を深めます。
こんにちは。wat(@watlablog)です。ここではガウス・ザイデル法を使って連立方程式を解く方法をPythonで実装します!
ガウス・ザイデル法の概要
ヤコビ法との違い
ガウス・ザイデル法(Gauss-Seidel Method)は「Pythonで連立方程式をヤコビ法(反復法)で解く方法」で紹介したヤコビ法とやっていることはほぼ変わりません。
収束判定の式や反復法における注意点も全く一緒です。
しかし、ヤコビ法の解き方にちょっとした工夫をすることで反復計算の回数が倍以上速くなる可能性を持ち、様々なソフトで使用されます。
ヤコビ法が解を求める際にnステップ目の解を使ってn+1ステップ目の解を求めるのに対し、ガウス・ザイデル法は1ステップ計算の最中に求まった最新の解を逐次使って計算するところが違いです。
…これは文章だとなかなか理解できそうにないので、式や図を使って考えてみましょう。
ガウス・ザイデル法の漸化式
連立方程式を書いて仕組みを理解する
ヤコビ法の記事でも行列形式でない連立方程式を書いて説明しましたが、ガウス・ザイデル法も式展開を追うことで理解を深めることが容易になります。是非紙とえんぴつで式を書いてみてください。
式(1)に例として3元連立方程式を示します。
式(2)と変形することで、それぞれの解を求める形になりました。
ここにステップ数を意味するように解に上添字を付けてみます。式(3)はヤコビ法の場合です。新しい\(n+1\)ステップ目の解を求めるために、\(n\)ステップ目の解を使っていることを表現しています。
続いて式(4)がガウス・ザイデル法の考え方です\(^{[1]}\)。このように、求まった\(n+1\)ステップ目の解を順次使いながら次々と逐次計算していくことで、ヤコビ法よりも真値に近づく可能性を高くすることが反復回数を少なくできる理由です。
前回同様係数行列に着目して図解してみた結果が下図です。nステップ目の解にかかる係数は係数行列の上三角成分、n+1ステップ目にかかる係数は係数行列の下三角成分となっているところに気付けば、この後のプログラミングがスムーズに進みます。
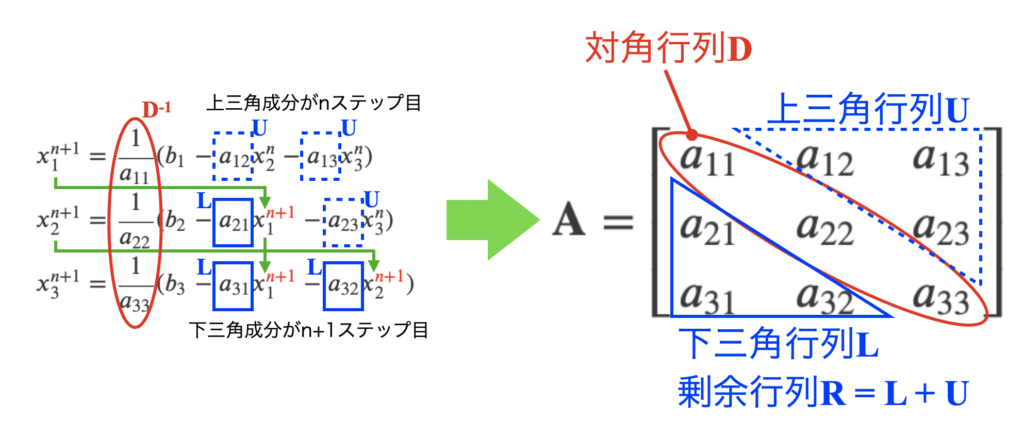
行列形式の漸化式
式(5)に式(4)をN元連立方程式に拡張した形を示します。
式はややこしく見えますが、右辺\(x^{n+1}\)にかかっている係数は係数行列の下三角成分、右辺\(x^{n}\)にかかっている係数は係数行列の上三角成分です。
三角形行列は三角形部分以外が全て0なので、わざわざ「係数行列や解ベクトルから○番目を抽出して…」といった処理は必要ありません。
また、今回はPythonのNumpyで実装します。内積計算が得意なNumpyを使うのでij成分を一つずつ抽出してダブルforループで計算等はあまりしたくありません。
Pythonで実装するために、式(5)を式(6)と変形します。
(ここからはあまり文献に答えが載っていなかったので、式の書き方は我流になっています。ご注意ください。)
下三角と上三角行列は三角形部分以外が0になっている特徴から、内積の計算結果は特に\(\mathbf{L}\)と\(\mathbf{U}\)に分けて計算しなくても\(n+1\)ステップ目の解と\(n\)ステップ目の解をうまく分類してくれます。
ただし、ループの中で最新の値を使うという意味で1行毎に計算を行う必要があり、\(i\)の下添字を明記しています。
ガウス・ザイデル法の注意点
反復法としての収束性等の注意点(ヤコビ法の記事で記載)以外に、ガウス・ザイデル法は並列計算ができないという注意点を持ちます。
これはガウス・ザイデル法が逐次直列的に解を求めていくことが原因ですが、この性質のために並列計算が可能なヤコビ法に計算速度の点でも負けてしまう可能性があります。
また、Python等のスクリプト言語では現状forループが遅いという欠点を持ちます。そのため、反復回数がいくら少なくても、forループを使わないで書くことが可能なヤコビ法に負ける可能性もあると思います(試していないですが)。
幸いPython開発チームは毎年のアップデートでこの欠点の改善に尽力していただいているようなので、改善はされると思います。
連立方程式をガウス・ザイデル法で反復的に解くPythonコード
動作環境
このページでは以下の環境で動作確認を行ったコードを掲載しています。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
サンプルコード
以下にガウス・ザイデル法で連立方程式を解くコードを示します。
答え合わせはnp.linalg.solveを使っています。
ポイントはforループで解を一つずつ求めているところです。こう書くことで解ベクトルの中身を更新しながら計算を行うことができます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 |
import numpy as np def gauss_seidel(A, b, tolerance): ''' 連立方程式をガウス・ザイデル法(反復法)で解く ''' # 係数行列を分解:D=対角成分ベクトル、R=剰余行列 D = np.diag(A) R = A - np.diag(D) # 初期化(適当な解と残差) x = np.random.random(len(b)) residual = 1e20 # 反復計算(逐次求めた解を次のループで使うため、forを使っている) iteration = 0 print('----------Start iteration----------') while residual > tolerance: # 収束判定用の1ステップ前の解を保持 x0 = x.copy() # 逐次計算 for i in range(len(x)): x[i] = (b[i] - R[i] @ x) / D[i] # 収束判定 residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2)) if iteration % 100 == 0: print('Iteration=', iteration) print('Residual=', residual) print('x=', x) iteration += 1 print('----------End iteration----------') print('Iteration=', iteration) print('Residual=', residual) print('x=', x, '\n') return x if __name__ == '__main__': # 係数行列と定数ベクトル A = np.array([[2, 1, 1], [2, 3, 1], [1, 1, 3]]) b = np.array([2, 4, -1]) # ガウス・ザイデル法で解を反復計算 x_gs = gauss_seidel(A, b, 1e-6) print('Gauss-Seidel method x=', x_gs, 'Validated b=', A @ x_gs) # numpyの線形代数ライブラリで検証 x_linalg = np.linalg.solve(A, b) print('np.linalg.solve x=', x_linalg, 'Validated b=', A @ x_linalg) |
このコードを実行すると以下の結果を得ます。
前回記事のヤコビ法で87回の反復計算を必要としていた方程式が、ガウス・ザイデル法は14回で収束しました。
|
1 2 3 4 5 6 7 8 9 10 11 |
----------Start iteration---------- Iteration= 0 Residual= 0.8778823774172507 x= [ 0.88604002 0.70039057 -0.86214353] ----------End iteration---------- Iteration= 14 Residual= 4.1748455267139336e-07 x= [ 1.00000038 0.99999981 -1.00000006] Gauss-Seidel method x= [ 1.00000038 0.99999981 -1.00000006] Validated b= [ 2.0000005 4.00000013 -1. ] np.linalg.solve x= [ 1. 1. -1.] Validated b= [ 2. 4. -1.] |
初期値に乱数を使っているので、実行毎に若干結果は変わりますが、これは明らかに計算回数が減ったと言えそうです。
ヤコビ法とガウス・ザイデル法の収束スピードを比較するコード
おまけとして、前回作成したヤコビ法と収束性(ステップ当たりの残差)を比較するコードを作ってみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
import numpy as np from matplotlib import pyplot as plt def jacobi(A, b, tolerance): ''' 連立方程式をヤコビ法(反復法)で解く ''' # 初期化(適当な解と残差) x0 = np.random.random(len(b)) residual = 1e20 # A = D + R D = np.diag(A) R = A - np.diag(D) # 反復計算=>残差がトレランスより小さくなったら終了 i = 0 print('----------Start iteration----------') res = [] while residual > tolerance: # 解と残差を計算 x = (b - (R @ x0)) / D residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2)) res.append(residual) if i % 100 == 0: print('Iteration=', i) print('Residual=', residual) print('x=', x) i += 1 x0 = x print('----------End iteration----------') print('Iteration=', i) print('Residual=', residual) print('x=', x, '\n') return x, res def gauss_seidel(A, b, tolerance): ''' 連立方程式をガウス・ザイデル法(反復法)で解く ''' # 係数行列を分解:D=対角成分ベクトル、R=剰余行列 D = np.diag(A) R = A - np.diag(D) # 初期化(適当な解と残差) x = np.random.random(len(b)) residual = 1e20 # 反復計算(逐次求めた解を次のループで使うため、forを使っている) iteration = 0 print('----------Start iteration----------') res = [] while residual > tolerance: # 収束判定用の1ステップ前の解を保持 x0 = x.copy() # 逐次計算 for i in range(len(x)): x[i] = (b[i] - R[i] @ x) / D[i] # 収束判定 residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2)) res.append(residual) if iteration % 100 == 0: print('Iteration=', iteration) print('Residual=', residual) print('x=', x) iteration += 1 print('----------End iteration----------') print('Iteration=', iteration) print('Residual=', residual) print('x=', x, '\n') return x, res def plot(r_jacobi, r_gauss_seidel): ''' Residualの変化をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Step') ax1.set_ylabel('Residual') # スケールの設定をする。 ax1.set_xlim(0, 120) #ax1.set_ylim(-0.2, 1.2) ax1.set_yscale('log') # プロットを行う。 x1 = np.arange(0, len(r_jacobi), 1) x2 = np.arange(0, len(r_gauss_seidel), 1) ax1.plot(x1, r_jacobi, label='Jacobi', lw=1, color='red') ax1.plot(x2, r_gauss_seidel, label='Gauss-Seidel', lw=1, color='blue') ax1.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() return if __name__ == '__main__': # 係数行列と定数ベクトル A = np.array([[2, 1, 1], [2, 3, 1], [1, 1, 3]]) b = np.array([2, 4, -1]) # ヤコビ法で解を反復計算 x_jacobi, res1 = jacobi(A, b, 1e-6) print('Jacobi method x=', x_jacobi, 'Validated b=', A @ x_jacobi) # ガウス・ザイデル法で解を反復計算 x_gs, res2 = gauss_seidel(A, b, 1e-6) print('Gauss-Seidel method x=', x_gs, 'Validated b=', A @ x_gs) plot(res1, res2) |
上記コードを実行するとmatplotlibによって以下のプロットを得ます。ガウス・ザイデル法はヤコビ法と比べてかなり速く収束している結果がわかります。
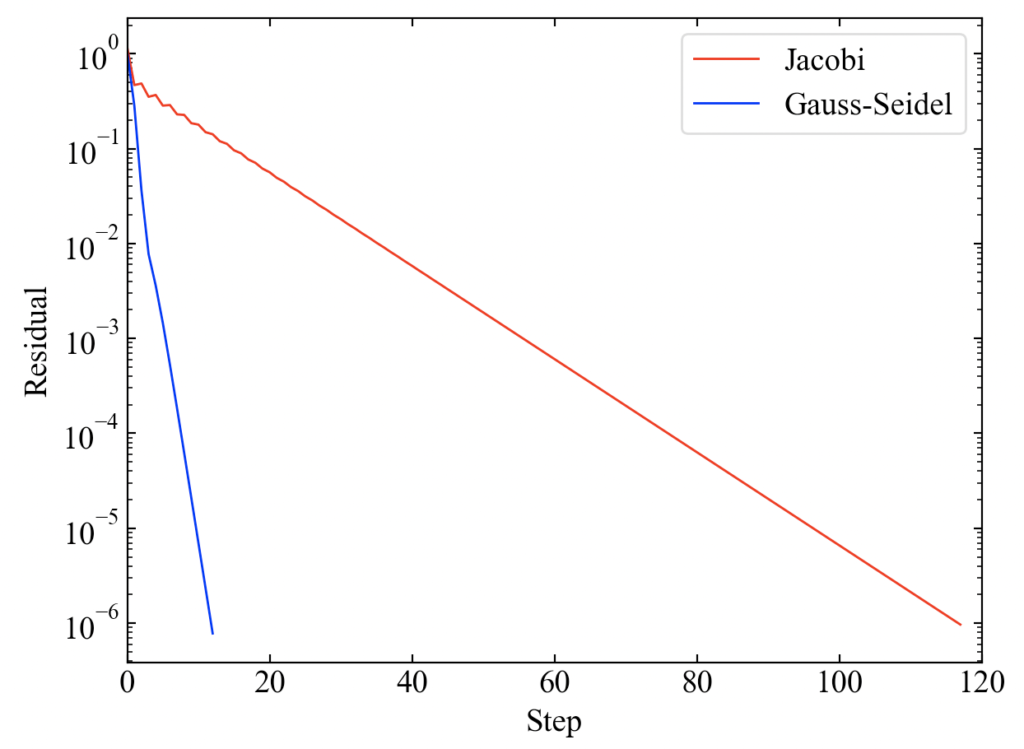
ネットを調べた結果はせいぜい2倍か3倍とのことでしたが、今回は噂を上回っています。(どちらかのコードで何か間違ったかな?)
問題の種類(未知数の数)、解ベクトルの初期値(実解との差)によって結果は変わりそうです。
また、今回ガウス・ザイデル法は1ステップを解ベクトルが一度全て求まった段階と定義しました(forループ終了時が1ステップとした)。
ヤコビ法はNumpyの行列演算でこの計算を一度に実施しているので、プログラム上の1ステップはforループの繰り返しもカウントすべきなのでしょうか?
この辺はプロにご教示願いたい!
まとめ
この記事では連立方程式を反復法で解くガウス・ザイデル法を解説しました。
前回のヤコビ法と対比させながら、式のどの部分が異なり計算数を削減するのかを式展開と図解で紹介しました。上三角や下三角の使い方を眺めてみると、ガウス・ザイデル法はヤコビ法と比べてよりプログラミングの考え方に近い漸化式であると感じました。
本プログラムは真値のわかっている方程式で検証し、我流ながら最後はPythonでガウス・ザイデル法を実装し、計算回数が減ることを確認しました。
参考文献
[1]山崎 郭滋, 偏微分方程式の数値解法入門, 森北出版株式会社, 2015, pp6
反復法にも色々な種類があることがわかりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!