Pythonで学ぶデータ同化の基礎！線形最小分散推定をやってみる

観測値とモデルの第1推定値を使って統計的に最適値を推定する「データ同化」という手法があります。ここでは基礎である線形最小分散推定を、初学者の筆者が理解した事をできるだけ噛み砕きながら、さらにPythonを使って実際にデータ処理を行ないながら紹介します。

こんにちは。wat(@watlablog)です。ここではデータ同化の基礎である線形最小分散推定を学習した結果を記録します！

目次（項目クリックでジャンプできます）

本記事の対象者

入門書の理解の助けが欲しい人

途中式を書いてみる

本記事の対象読者は僕と同じくデータ同化分野の初学者です。

データ同化のイメージを図解する

僕は今までデータ同化という言葉すらあまり知りませんでした。ただ、「シミュレート・ジ・アース」という科学系書籍を読み、興味が湧いてきました。

シミュレート・ジ・アース―未来を予測する地球科学

私たちはどこまで将来のことがわかっているのか。地球の未来を予測する地球科学の最新トピックスを、ひとつひとつ丁寧に解説する、あなたの知的好奇心をくすぐる一冊です。

Amazon

楽天

この本ではデータ同化の最初の説明に、以下の文章がありました。

----観測データとのずれがもっとも小さくなるような計算結果を、予測のための初期値とするのです。
河宮未知生, シミュレート・ジ・アース, ベレ出版, pp84, (2018)

僕は日々企業でシミュレーションをしたり、検証で実験をしたりと、モデル予測値と観測値を両方扱っていたので、気象予報で使われている最新のシミュレーション手法に様々な観測値の情報を取り入れている事に感動しました。

ここではシミュレーション屋さん、実験屋さんの両方の観点で、僕が理解していった内容をできるだけ図解して説明しようと思います。

筆者の購入した参考書

僕は以下の書籍を購入しました。まずはこの本から学習していきます。今後増えるかも知れません。

データ同化―観測・実験とモデルを融合するイノベーション

この本で,データの合わせ技ができる新技法,データ同化がしっかりと実感できます.基礎理論を学ぶ方,データ同化を切り口として最適化問題に取り組む方,海洋,気象,地震,さらには魚の問題にまで応用したい方,本書はそういう方々にぜひお勧めした最適の教科書です.

Amazon

楽天

Pythonで実際に処理を体験したい人

正直、式だけだとよくわからない事が多いです。言っている事が結局どういう事なのか、自分でデータ処理をしてみて動作を確認する事ができれば、理解も早くなると思います。

そのため、この記事では手始めにデータ同化の考え方の基礎中の基礎である線形最小分散推定という処理を、Pythonで書いてみます。

Pythonで書く理由は~~当ブログのアイデンティティだから~~プログラミングのハードルが異常なほど低いからです。

それでは、ここからデータ同化のイメージ説明、線形最小分散推定の式展開、Pythonによる例題コーディングを行なっていきます。

データ同化のイメージ

データ同化と機械学習の違い

ここではデータ同化のイメージを掴むために、個人的に理解した内容を書いていきます。少々本質とは異なる記述になってしまうかも知れませんが、イメージを固めてから式を見るのが有効と思っています。

データ同化は世間を賑わせている機械学習との対比をする事で理解が深まると思います。

どちらもデータとモデルを扱うのは同じですが、まずは機械学習のおさらいをしましょう。

機械学習は大量の観測データからモデルをつくる

まずは機械学習(Machine Learning)です。

機械学習とは、大量の観測値を使って回帰モデルや分類モデルをつくる技術が主な内容です。

まずはデータがなければ話にならないのですが、詳細な物理モデル等がなくても機能するというメリットがあります。

以下のGIF動画は、ディープニューラルネットワークによって大量の観測値に適合するモデルを学習により作成した例です。初期モデルからは全くデータ群の形を想像できませんが、反復計算により次第にモデルがデータにフィットしてくることがよくわかります。

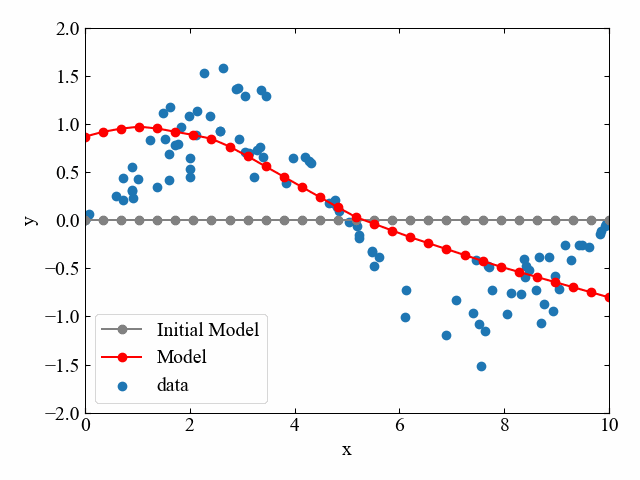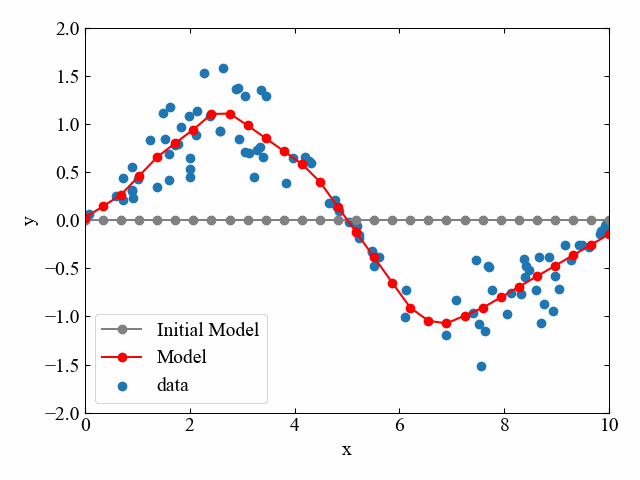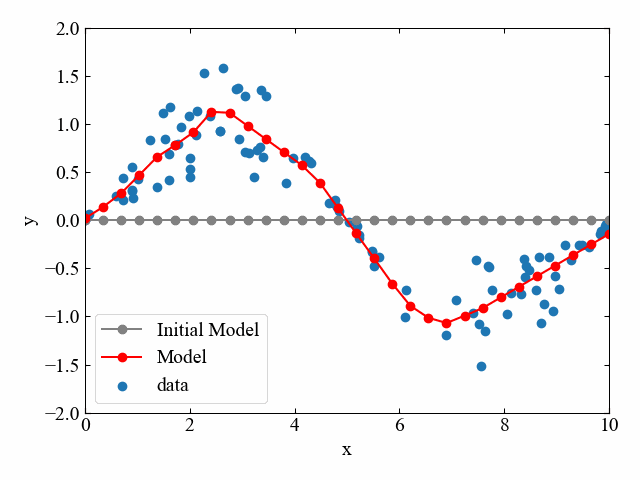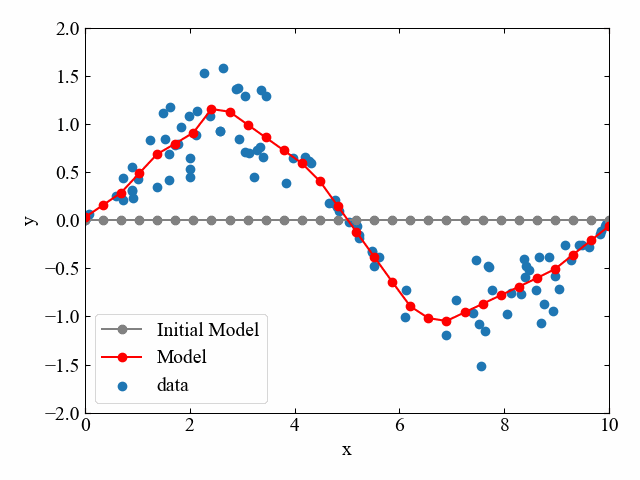
ちなみにこの内容は「PyTorchで色々な非線形関数を回帰してみたらすごかった」という記事でPython/PyTorchによるコードを紹介していますので、是非みてみて下さい。

データ同化は予測モデルと観測値から真値を予測する

データ同化(Data Assimilation)は機械学習ほど大量のデータを必要としませんが（あれば尚良いのでしょうが）、ある程度科学的な根拠をもった優秀なモデルが必要です。

下図は僕が理解したデータ同化のイメージ図です。

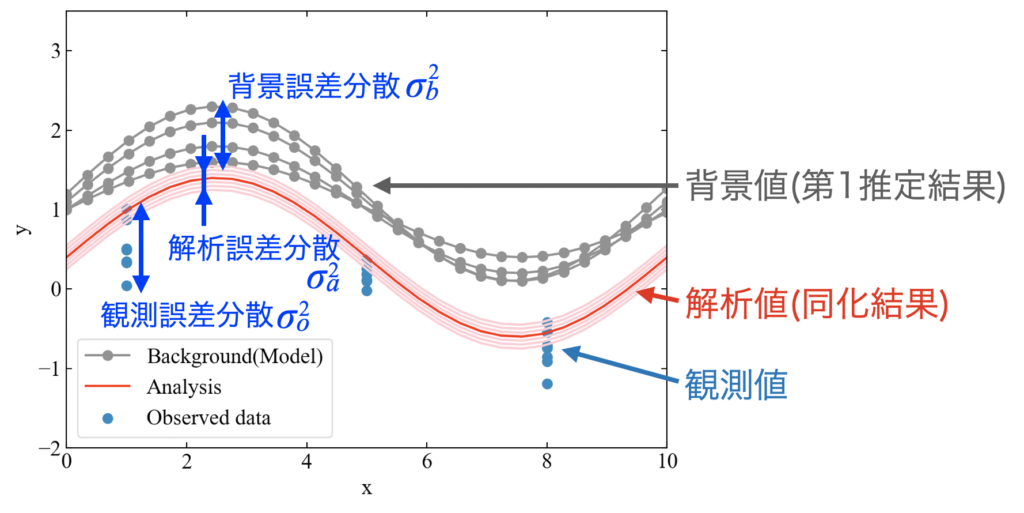
ここで示している背景値とは、例えば物理モデルのシミュレーション結果を指します。物理モデルは様々なパラメータを持ち、通常は全ての値を正確に同定する事が困難であるため、取り得る値は一意に決まらずに分散を持つ事になります。この分散の事を背景誤差分散\(\sigma_{b}^{2}\)と呼びます。
※分散＝標準偏差の二乗

モデルなのに分散を持つ具体的な例はまだぼんやりですが、工学系の数値モデルであればメッシュの条件、乱流モデルのパラメータ、材料物性、荷重条件, etc.…とかですかね？

対して観測値にも分散があり、これを観測誤差分散\(\sigma_{o}^{2}\)と呼びます。
実験データには測定器、測定対象の条件…によって様々な誤差が含まれるので、実験屋さんとしてはおなじみだと思います。

そして、データ同化では背景値と観測値、それぞれの誤差分散の情報から解析値を算出します。分散の情報はこの解析値にも含まれ、これを解析誤差分散\(\sigma_{a}^{2}\)と呼びます。

解析誤差分散は背景誤差分散と観測誤差分散より小さくなる特徴があり、同化後の結果はより信頼区間の狭い精度の高い予測ができるという事になります。

それではここで説明した概念の基礎である線形最小分散推定について式を見ていきましょう。

線形最小分散推定の式展開

線形最小分散推定とは、真値を背景値と観測値の線形結合で表し、分散を最小にするように推定する手法です。データ同化の基本原理の１つなので導入部から式展開をしていきます。

誤差と仮定を導入する

まずは実験等で得られる観測値\(x_{o}\)、モデル等の第1推定値である背景値\(x_{b}\)は、真値\(x_{true}\)に対しては、それぞれ観測値が持つ誤差\(\epsilon_{o}\)、背景値が持つ誤差\(\epsilon_{b}\)を導入すると、式(1)と書けます。

\[ x_{o}=x_{true}+\epsilon_{o}\\ x_{b}=x_{true}+\epsilon_{b} \tag{1} \]

ここで、観測値\(x_{o}\)、背景値\(x_{b}\)の平均値は共に真値\(x_{true}\)に等しいという仮定を置きます。ここで言う平均値は確率的に多数の試行回数で収束する値の事なので、期待値とも言う事が出来ます。

期待値は数式上ブラケット「\(\left \langle \right \rangle\)」を使って書くので、式(2)の関係式を仮定した事になります。ちなみにこのような量\(x_{o}\)、\(x_{b}\)の事を不偏推定量とも呼びます。

\[ \left \langle x_{o} \right \rangle = \left \langle x_{b} \right \rangle = x_{true} \tag{2} \]

式(2)を仮定した事で、式(1)の誤差\(\epsilon_{o}\)、\(\epsilon_{b}\)の期待値も式(3)と書く事が可能です。

\[ \left \langle \epsilon_{o} \right \rangle = \left \langle \epsilon_{b} \right \rangle = 0 \tag{3} \]

次に、観測値\(x_{o}\)、背景値\(x_{b}\)の誤差は無相関であるという仮定も導入します。この言葉を共分散の書き方で表現すると、式(4)となります。

\[ \left \langle (x_{o}-x_{true})(x_{b}-x_{true}) \right \rangle = 0 \tag{4} \]

式(4)は式(1)に代入する事で、誤差\(\epsilon\)を使った式(5)の関係式を得ます。

\[ \left \langle \epsilon_{o}\epsilon_{b} \right \rangle = 0 \tag{5} \]

解析値を観測値と背景値の線形結合で表現する

以上の2つの仮定を置いた上で、解析値\(x_{a}\)を観測値\(x_{o}\)と背景値\(x_{b}\)の重み付き線形結合で示した式(6)について、解析値の誤差分散\(\sigma_{a}^{2}\)を最小にする重みを求める事が最適解を求める事になり、最小分散推定の手法となります。

\[ x_{a} = \alpha_{1} x_{o} + \alpha_{2} x_{b} \tag{6} \]

ここで、\(x_{o}\)と\(x_{b}\)の期待値は\(x_{true}\)になる（式(2)）事と、これから推定したい解析値\(x_{a}\)の期待値も真値\(x_{true}\)とすると、\(x_{a}\)も同じく不偏推定量（推定量の平均値が母集団の平均値に等しい）となるため、重み\(\alpha\)は式(7)の関係となります。

\[ \alpha_{1}+\alpha_{2}=1 \tag{7} \]

式(7)を用いて式(6)を単一の\(\alpha\)で表すと式(8)となります。
この式を用いて線形最小分散推定を行っていきます。

\[ x_{a} = \alpha_{1} x_{o} + (1-\alpha_{1}) x_{b} \tag{8} \]

解析値の誤差分散を定義する

ここまでで解析値\(x_{a}\)の式を立てましたが、線形最小分散推定は解析値の誤差分散を最小にする必要があります。

解析値の誤差は解析値と真値との差なので、まずは式(8)の観測値と背景値から真値を引き、式(9)と両辺を誤差で表現します。

\[ \begin{eqnarray} x_{a}-x_{true} &=&\alpha_{1} (x_{o}-x_{true}) + (1-\alpha_{1}) (x_{b}-x_{true})\\ \epsilon_{a} &=&\alpha_{1} \epsilon_{o} + (1-\alpha_{1}) \epsilon_{b} \tag{9} \end{eqnarray} \]

次に式(10)と誤差の二乗をとります。

\[ \begin{eqnarray} \epsilon_{a}^{2} &=& \left \{ \alpha_{1} \epsilon_{o} + (1-\alpha_{1}) \epsilon_{b} \right \}^{2}\\ &=& \alpha_{1}^{2} \epsilon_{o} ^{2} + 2\alpha_{1} \epsilon_{o}\epsilon_{b}(1-\alpha_{1})+(1-\alpha_{1})^{2}\epsilon_{b}^{2} \tag{10} \end{eqnarray} \]

誤差分散は期待値を使って式(11)と書き、

\[ \left \langle \epsilon_{a}^{2}\right \rangle = \alpha_{1}^{2} \left \langle\epsilon_{o} ^{2}\right \rangle + 2\alpha_{1} \left \langle\epsilon_{o}\epsilon_{b}\right \rangle(1-\alpha_{1})+(1-\alpha_{1})^{2}\left \langle\epsilon_{b}^{2}\right \rangle\\ \tag{11} \]

\(\epsilon_{o}\)と\(\epsilon_{b}\)はそれぞれ無相関であるという仮定から、\(\left \langle\epsilon_{o}\epsilon_{b}\right \rangle=0\)(式(5))が成立、さらに誤差分散を\(\sigma^{2}\)で表現する事で、式(12)が導出されます。

\[ \sigma_{a}^{2}=\alpha_{1}^{2}\sigma_{o}^{2} + (1-\alpha_{1})^{2}\sigma_{b}^{2} \tag{12} \]

微分して重みの最小値を求める

式(12)の\(\sigma_{a}^{2}\)を最小化する重み\(\alpha_{1}\)を導出します。

最小値を求めるために、式(12)を\(\alpha_{1}\)の関数と見なし、微分して0になる式(13)を立てて、\(\alpha_{1}\)の式に変形します。合成関数の微分を使えば高校数学の範囲で出来ますね。

\[ \begin{eqnarray} \frac{\mathrm{d} \sigma_{a}^{2}}{\mathrm{d} \alpha_{1}}=2\alpha_{1}\sigma_{o}^{2}+2(\alpha_{1}-1)\sigma_{b}^{2}&=&0\\ \alpha_{1}\sigma_{o}^{2}+\alpha_{1}\sigma_{b}^{2}-\sigma_{b}^{2}&=&0\\ \alpha_{1}(\sigma_{o}^{2}+\sigma_{b}^{2})&=&\sigma_{b}^{2}\\ \alpha_{1}&=&\frac{\sigma_{b}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}} \tag{13} \end{eqnarray} \]

\(\alpha_{1}\)が求められたら\(\alpha_{2}\)も式(14)で求める事ができます。

\[ \begin{eqnarray} \alpha_{2}&=&1-\alpha_{1}\\ &=&1-\frac{\sigma_{b}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}}\\ &=&\frac{\sigma_{o}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}}\tag{14} \end{eqnarray} \]

最適推定値を導出する

式(13)と式(14)で求めた重みを式(8)に代入する事で、式(15)と線形最小分散推定の解析値を求める事ができます。

\[ \begin{eqnarray} x_{a} &=& \frac{\sigma_{b}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}} x_{o} + \frac{\sigma_{o}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}} x_{b}\\ &=&x_{b} + \frac{\sigma_{b}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}} (x_{o}-x_{b}) \tag{15} \end{eqnarray} \]

式(15)を2行目までまとめたのは意味があります。

式(15)は背景値\(x_{b}\)に解析インクリメントと呼ばれる項を足す事で解析値が算出されるという解釈をします。そして、解析インクリメントは観測値\(x_{o}\)と背景値\(x_{b}\)の差（これをイノベーションと呼ぶ）とそれぞれの誤差分散で構成されています。

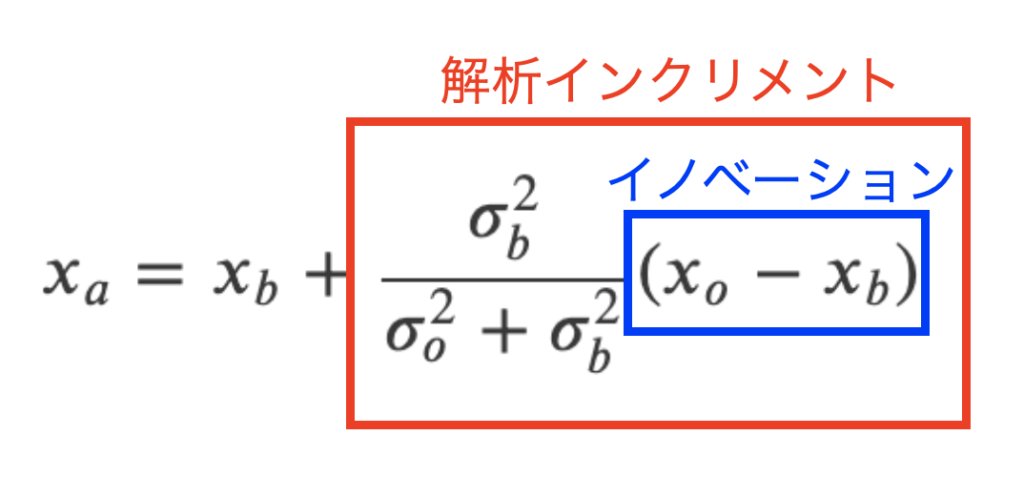
モデルの第1推定値を更新する、という意味合いを持つ式になったと思います。

解析値の誤差分散を導出する

最後に、式(12)をスタート地点として、解析値の誤差分散を式(16)と求めます。

\[ \begin{eqnarray} \sigma_{a}^{2}&=&\alpha_{1}^{2}\sigma_{o}^{2} + (1-\alpha_{1})^{2}\sigma_{b}^{2}\\ &=&\left \{\frac{\sigma_{b}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}}\right \}^{2}\sigma_{o}^{2} + \left \{\frac{\sigma_{o}^{2}}{\sigma_{o}^{2}+\sigma_{b}^{2}}\right \}^{2}\sigma_{b}\\ &=&\frac{\sigma_{b}^{2}\sigma_{o}^{4}+\sigma_{b}^{4}\sigma_{o}^{2}}{(\sigma_{b}^{2}+\sigma_{o}^{2})^{2}}\\ &=&\frac{\sigma_{b}^{2}\sigma_{o}^{2}(\sigma_{b}^{2}+\sigma_{o}^{2})}{(\sigma_{b}^{2}+\sigma_{o}^{2})^{2}}\\ &=&\frac{\sigma_{b}^{2}\sigma_{o}^{2}}{\sigma_{b}^{2}+\sigma_{o}^{2}} \tag{16} \end{eqnarray} \]

以上で式展開は終了です。ここからはPythonで実際にデータを処理しながら式の効果を見ていきましょう！

線形最小分散推定の効果を確認するPythonコード

ここではPythonを使って実際に線形最小分散推定を体験してみましょう。
解析値は本当に分散が小さくなるのか、観測値と背景値にギャップがある場合はどのように解析値の分布が来るのか…これを理解するにはヒストグラムによるプロットが適しています。

Pythonであれば大量の試行回数を必要とする実験も擬似乱数でちょちょいのちょいです。

動作環境

コードを実行した時のこちらの動作環境を参考に記載します。

Windows

Windows	OS	Windows10 64bit
	CPU	2.4[GHz]
	メモリ	4[GB]

Mac

Mac	OS	macOS Catalina 10.15.7
	CPU	1.4[GHz]
	メモリ	8[GB]

Python環境

Pythonの外部ライブラリはNumpyとmatplotlibのみを使用しています。

Python	Python 3.7.7
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.19.0
matplotlib	3.2.2

全コード

以下のコードは線形最小分散推定を行う関数をdef文で定義しています。
そして観測値と背景値はnp.random.normalを使ってガウス分布を持つサンプルデータとして生成しています。このメソッドを使う事で意図的に平均値にずれを持たせたり、標準偏差を変更したりといった効果を出す事ができます。

ガウス分布を持つノイズの作り方の詳細は「Pythonでガウス分布を持つノイズの作り方と調整方法」をご覧ください。

import numpy as np
from matplotlib import pyplot as plt

# 線形最小分散推定をする関数
def linear_min_variance_estimation(x_o, x_b):
    var_o = np.std(x_o) ** 2                                # 観測誤差分散
    var_b = np.std(x_b) ** 2                                # 背景誤差分散

    x_a = x_b + (var_b / (var_o + var_b)) * (x_o - x_b)     # 解析値
    var_a = (var_b * var_o) / (var_b + var_o)               # 解析誤差分散

    return x_a, var_a

# 観測値と背景値を10万点のサンプルデータで作成
n = np.arange(1, 100001, 1)
x_o = np.random.normal(loc=10, scale=15, size=len(n))
x_b = np.random.normal(loc=-10, scale=10, size=len(n))

# 解析値と解析誤差分散を求める関数
x_a, var_a = linear_min_variance_estimation(x_o, x_b)

# 理論解析誤差分散と実際に計算された解析誤差分散をコンソールに表示
print('estimated variance=', var_a, 'measured variance=', np.std(x_a) ** 2)

# ここからグラフ描画-------------------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('x')
ax1.set_ylabel('count')

# データプロット
ax1.hist(x_o, bins=50, range=(-60, 60), histtype='step', label='Observed', color='blue')
ax1.hist(x_b, bins=50, range=(-60, 60), histtype='step', label='Model estimation', color='green')
ax1.hist(x_a, bins=50, range=(-60, 60), histtype='step', label='Optimal estimation', color='red', lw=4)

# グラフを表示する。
ax1.legend()
fig.tight_layout()
plt.show()
plt.close()
# -------------------------------------------------------------------

import numpy as np

from matplotlib import pyplot as plt

# 線形最小分散推定をする関数

def linear_min_variance_estimation(x_o, x_b):

var_o = np.std(x_o) ** 2 # 観測誤差分散

var_b = np.std(x_b) ** 2 # 背景誤差分散

x_a = x_b + (var_b / (var_o + var_b)) * (x_o - x_b) # 解析値

var_a = (var_b * var_o) / (var_b + var_o) # 解析誤差分散

return x_a, var_a

# 観測値と背景値を10万点のサンプルデータで作成

n = np.arange(1, 100001, 1)

x_o = np.random.normal(loc=10, scale=15, size=len(n))

x_b = np.random.normal(loc=-10, scale=10, size=len(n))

# 解析値と解析誤差分散を求める関数

x_a, var_a = linear_min_variance_estimation(x_o, x_b)

# 理論解析誤差分散と実際に計算された解析誤差分散をコンソールに表示

print('estimated variance=', var_a, 'measured variance=', np.std(x_a) ** 2)

# ここからグラフ描画-------------------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('x')

ax1.set_ylabel('count')

# データプロット

ax1.hist(x_o, bins=50, range=(-60, 60), histtype='step', label='Observed', color='blue')

ax1.hist(x_b, bins=50, range=(-60, 60), histtype='step', label='Model estimation', color='green')

ax1.hist(x_a, bins=50, range=(-60, 60), histtype='step', label='Optimal estimation', color='red', lw=4)

# グラフを表示する。

ax1.legend()

fig.tight_layout()

plt.show()

plt.close()

# -------------------------------------------------------------------

実行結果

以下がコードを実行して得られる結果です。赤で示した解析値は観測値や背景値（モデル予測値）よりも最頻値が高くなっており、平均値も観測値と背景値の間に来ています。同一データ数で解析値の方が最頻値が高く出ているという事で、分散も小さくなっている事がわかると思います。

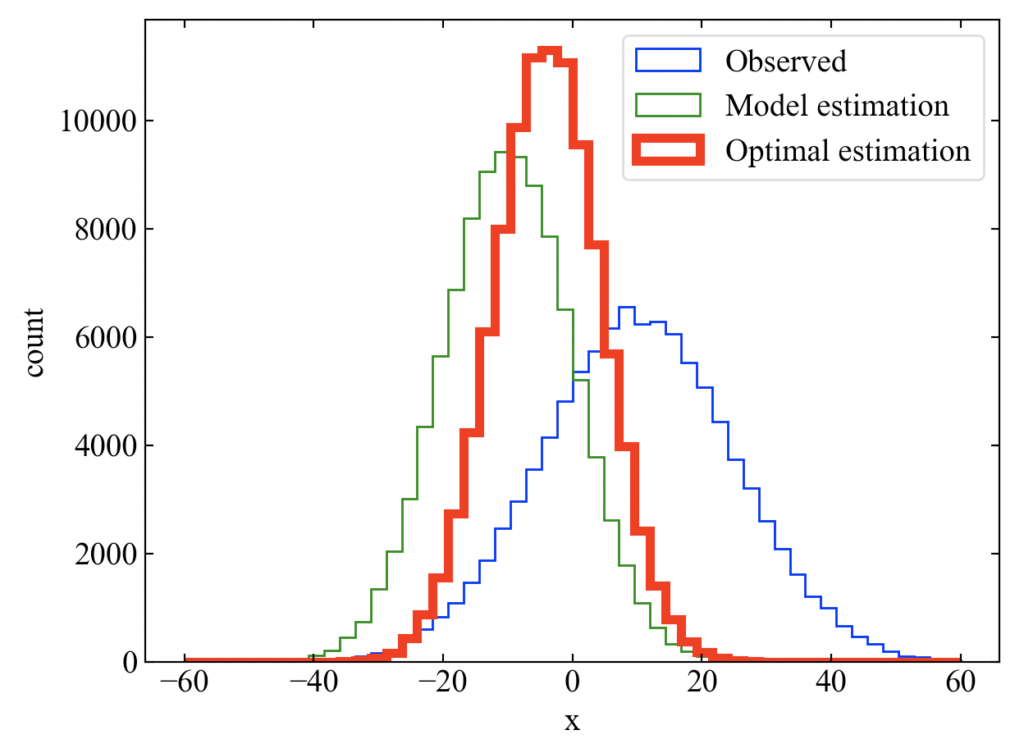
ちなみにコンソールにはprint文の中身として以下が表示されました。
これは式(16)で計算された解析誤差分散と、実際に観測値と背景値で計算された生データから分散をnp.std()**2で求めた結果です。非常に近い値が得られ、式(16)の確からしさが確認できました。

estimated variance= 69.15062373551417
measured variance= 69.41385854253596

1 2	estimated variance= 69.15062373551417 measured variance= 69.41385854253596

まとめ

この記事ではデータ同化って何なのかよくわからないという人を対象に、まずイメージを掴むための機械学習との違いを紹介しました。

データ同化は目的に応じて様々なケースに使われますが、この記事ではモデルを使ったシミュレーション予測値と実験で得られる観測値というデータを使う事を前提に記事構成をしてみました。

基礎の基礎である線形最小分散推定について、一連の式展開は書籍以外にもインターネットの様々な記事、Youtube動画で多数公開されている既知の内容ですが、この記事ではできるだけ途中式を省かずに書いてみました。

数学の得意な方からすればかなりスマートさやエレガントさに欠ける見難い式展開になっているかも知れませんが、僕のように数学の超苦手な人（理系のはずなのに）にとっては躓かずに進める内容になったのではないでしょうか。

最後にPythonコードによる体験ができるように記事構成する事で、読者の皆様が実際に平均や標準偏差を変えた実験ができるようにしてみました。

まだPythonを使った事の無い方は、是非これを機にPythonも覚えてみてはいかがでしょうか？
→ご興味のある方は当ブログ「Pythonカテゴリ」へ足を運んでみて下さい。

まだまだ基礎中の基礎だけですが、データ同化という面白い分野に入門してみました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！