
質点の振動を運動方程式で記述する時、結構面倒なのが剛性行列の作成だと思います。ここでは振動の勉強がてら、Python/Sympyを使った剛性行列自動生成をしてみた方法を紹介します。
こんにちは。wat(@watlablog)です。今回はSymPyを使って運動方程式の剛性行列を作成する方法を紹介します!
事前準備
質点の振動系で扱う運動方程式
まずはじめに、質点の振動系で扱う運動方程式をおさらいしておきます。
当ブログの工学カテゴリではお馴染みの下図。これは2自由度の振動系です。
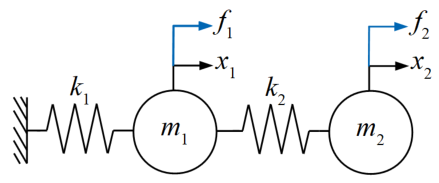
運動方程式は各質点周りの力の関係を\(F=ma\)に習って書き下すため、まずは2つの質点について下式を書く事が出来ます。
上の式を展開してそれぞれの加速度、変位にかかっている共通の係数を抽出する事で、以下の連立方程式にする事が可能です。
これをかっこよく書くと、下式になります。今回自動生成するのは剛性行列\(\mathbf{K}\)です。
この辺の話は別途「Pythonで計算するために多自由度振動系を行列形式にする方法」にまとめていますので、ちょっとあやしくなったら戻って読み直しましょう!
SymPyのおさらい
SymPyとは、数式を記号(Symbol)そのままで表現でき、式の展開や計算、その他数学的処理を行う事ができるライブラリです。
当ブログでは「Python/sympyでテイラー展開した結果をグラフ化する方法」でテイラー展開をやってみたり、「Python/sympyとnumpyで書くニュートン-ラフソン法」でニュートン・ラフソン法を書いてみたりしました。
SymPyでどんな事ができるか不明な場合は是非上記記事をご覧下さい。
今回は数式処理をSymPyでやってみます。
本記事の目標
式変形のミスを無くす
僕は注意散漫のようで、よく式展開中に符号ミスをやらかします。すると剛性行列を算出する部分でモデル上の整合性がくずれ、シミュレーション結果が間違ってしまう事になります。
おそらく常日頃からこういった手計算をしている人にとっては造作もない事なのかも知れませんが、たまにしかやらない人にとっては面倒事の一つです。
SymPyを使って、記号ベースで自動計算する事で少なくとも式変形自体のミスは無くなるはず、というのが最初のモチベーションです。
NumPy形式の剛性行列式を得る
Pythonで多自由度系の振動シミュレーションを行う時、大抵は質量、減衰、剛性行列を生成し関数に投げてがちゃがちゃ計算しますが、複数自由度になるとこの行列をNumPy形式で書くのも面倒です(僕がどんだけ面倒くさがりかわかってしまう…)。
NumPy形式の行列というのは、[[k1+k2, -k2],[-k2, k2]]といった形式のものです。自由度が少なければ良いのですが、多くなると大変です。6自由度の問題を解く場合、36個も入力しないとなりません。
そのため今回は自動でNumPy形式の行列を得る、も目標とします。
質量行列と減衰行列について
今回剛性行列に絞って書いていますが、質量行列は通常離散化されているため対角になる、減衰行列は剛性行列と同じ考え方で生成するため、ここでは特に取り扱っていません。
SymPyで剛性行列を自動生成するコード
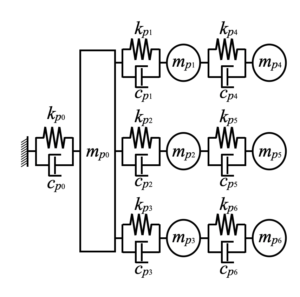
問題:7自由度振動モデル
まず対象とする問題のモデルを以下に示します。いつも直列に繋がった問題ばかり扱っていたので、今回は異なるタイプを試してみます。全部で7自由度あります(大変そう…)。
変数を定義する
今回の7自由度モデルで使う変数を定義します。importでSymPy(後で使うNumPyも)を入れて、以下を定義します。基本は変位\(x\)とばね定数\(k\)しか計算に使わないのですが、物理的な式の整合性のために他の変数も入れています。
モデル上減衰係数もありますが、無視(必要な場合は本コードを減衰版でもう一回走らせればOK)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
from sympy import* import numpy as np # 変数リスト-------------------------------------------------------------------------------- # xの変数を定義 x_p0, x_p1, x_p2, x_p3, x_p4, x_p5, x_p6 = symbols('x_p0 x_p1 x_p2 x_p3 x_p4 x_p5 x_p6') x = [x_p0, x_p1, x_p2, x_p3, x_p4, x_p5, x_p6] # kの変数を定義 k_p0, k_p1, k_p2, k_p3, k_p4, k_p5, k_p6 = symbols('k_p0 k_p1 k_p2 k_p3 k_p4 k_p5 k_p6') # aの変数を定義(今回使わないけど式の整合ののために定義) a_p0, a_p1, a_p2, a_p3, a_p4, a_p5, a_p6 = symbols('a_p0 a_p1 a_p2 a_p3 a_p4 a_p5 a_p6') # mの変数を定義(今回使わないけど式の整合ののために定義) m_p0, m_p1, m_p2, m_p3, m_p4, m_p5, m_p6 = symbols('m_p0 m_p1 m_p2 m_p3 m_p4 m_p5 m_p6') # fの変数を定義(今回使わないけど式の整合ののために定義) f_p0, f_p1, f_p2, f_p3, f_p4, f_p5, f_p6 = symbols('f_p0 f_p1 f_p2 f_p3 f_p4 f_p5 f_p6') |
運動方程式を立てる
剛性行列を自動生成するといっても、モデルの接続方法から定義するわけではないので、自分で運動方程式は立てます。そこまでやったら最後まで手で計算しろというツッコミは今は無しで…。
但し、ここでは素直にモデルの力関係を読んだ通りに書きます。式の展開や整理はやりませんので、以下の式で止めてOK。
ここでミスってたら一発KO。仕事や研究で使う場合等はよく自分で確認しましょう(普段ガンガン書くわけでは無いので、上記も僕が間違っている可能性あります)。
先ほど定義した変数を使ってSymPyで書くと以下のようになります。質量と加速度の積は右側に移項して0=の形にして右辺を変数にしています。
最後にeqとして全式をリストにまとめます。
|
1 2 3 4 5 6 7 8 9 10 |
# 運動方程式をモデルを読んだ通りに書く---------------------------------------------------------- eq_p0 = f_p0 - k_p0 * x_p0 + k_p1 * (x_p1 - x_p0) + k_p2 * (x_p2 - x_p0) + k_p3 * (x_p3 - x_p0) - m_p0 * a_p0 eq_p1 = f_p1 - k_p1 * (x_p1 - x_p0) + k_p4 * (x_p4 - x_p1) - m_p1 * a_p1 eq_p2 = f_p2 - k_p2 * (x_p2 - x_p0) + k_p5 * (x_p5 - x_p2) - m_p2 * a_p2 eq_p3 = f_p3 - k_p3 * (x_p3 - x_p0) + k_p6 * (x_p6 - x_p3) - m_p3 * a_p3 eq_p4 = f_p4 - k_p4 * (x_p4 - x_p1) - m_p4 * a_p4 eq_p5 = f_p5 - k_p5 * (x_p5 - x_p1) - m_p5 * a_p5 eq_p6 = f_p6 - k_p6 * (x_p6 - x_p1) - m_p6 * a_p6 eq = [eq_p0, eq_p1, eq_p2, eq_p3, eq_p4, eq_p5, eq_p6] |
剛性行列生成(展開と係数抽出)
次で最後。generate_k_matrix関数に式リストと係数抽出をしたいxリストを渡して実行します。
|
1 2 3 4 5 6 7 8 9 10 11 |
def generate_k_matrix(eq, x): K = Matrix(np.zeros((len(x), len(x)))) for i in range(len(eq)): for j in range(len(x)): K[i, j] = - expand(eq[i]).coeff(x[j]) return K # 剛性マトリクスを生成する関数を実行 K = generate_k_matrix(eq, x) print(K) |
全コードと結果
以下にコピペしてすぐ動かせるように全コードを載せておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 |
from sympy import* import numpy as np def generate_k_matrix(eq, x): K = Matrix(np.zeros((len(x), len(x)))) for i in range(len(eq)): for j in range(len(x)): K[i, j] = - expand(eq[i]).coeff(x[j]) return K # 変数リスト-------------------------------------------------------------------------------- # xの変数を定義 x_p0, x_p1, x_p2, x_p3, x_p4, x_p5, x_p6 = symbols('x_p0 x_p1 x_p2 x_p3 x_p4 x_p5 x_p6') x = [x_p0, x_p1, x_p2, x_p3, x_p4, x_p5, x_p6] # kの変数を定義 k_p0, k_p1, k_p2, k_p3, k_p4, k_p5, k_p6 = symbols('k_p0 k_p1 k_p2 k_p3 k_p4 k_p5 k_p6') # aの変数を定義(今回使わないけど式の整合ののために定義) a_p0, a_p1, a_p2, a_p3, a_p4, a_p5, a_p6 = symbols('a_p0 a_p1 a_p2 a_p3 a_p4 a_p5 a_p6') # mの変数を定義(今回使わないけど式の整合ののために定義) m_p0, m_p1, m_p2, m_p3, m_p4, m_p5, m_p6 = symbols('m_p0 m_p1 m_p2 m_p3 m_p4 m_p5 m_p6') # fの変数を定義(今回使わないけど式の整合ののために定義) f_p0, f_p1, f_p2, f_p3, f_p4, f_p5, f_p6 = symbols('f_p0 f_p1 f_p2 f_p3 f_p4 f_p5 f_p6') # 運動方程式をモデルを読んだ通りに書く---------------------------------------------------------- eq_p0 = f_p0 - k_p0 * x_p0 + k_p1 * (x_p1 - x_p0) + k_p2 * (x_p2 - x_p0) + k_p3 * (x_p3 - x_p0) - m_p0 * a_p0 eq_p1 = f_p1 - k_p1 * (x_p1 - x_p0) + k_p4 * (x_p4 - x_p1) - m_p1 * a_p1 eq_p2 = f_p2 - k_p2 * (x_p2 - x_p0) + k_p5 * (x_p5 - x_p2) - m_p2 * a_p2 eq_p3 = f_p3 - k_p3 * (x_p3 - x_p0) + k_p6 * (x_p6 - x_p3) - m_p3 * a_p3 eq_p4 = f_p4 - k_p4 * (x_p4 - x_p1) - m_p4 * a_p4 eq_p5 = f_p5 - k_p5 * (x_p5 - x_p1) - m_p5 * a_p5 eq_p6 = f_p6 - k_p6 * (x_p6 - x_p1) - m_p6 * a_p6 eq = [eq_p0, eq_p1, eq_p2, eq_p3, eq_p4, eq_p5, eq_p6] # 剛性マトリクスを生成する関数を実行 K = generate_k_matrix(eq, x) print(K) |
求めたい剛性行列はprint文の出力結果です。
Matrix()の中身は「[]」でまとめられており、このままPythonコードに貼り付ける事で別のプログラムで変数として定義する事ができそうですね。目標達成。
|
1 2 3 4 5 6 7 |
Matrix([[k_p0 + k_p1 + k_p2 + k_p3, -k_p1, -k_p2, -k_p3, 0, 0, 0], [-k_p1, k_p1 + k_p4, 0, 0, -k_p4, 0, 0], [-k_p2, 0, k_p2 + k_p5, 0, 0, -k_p5, 0], [-k_p3, 0, 0, k_p3 + k_p6, 0, 0, -k_p6], [0, -k_p4, 0, 0, k_p4, 0, 0], [0, -k_p5, 0, 0, 0, k_p5, 0], [0, -k_p6, 0, 0, 0, 0, k_p6]]) |
LaTeX形式で書くと以下のようになります。
機械力学ハンドブックとか読むと、実は剛性行列は各点の重ね合わせで表現できるそうなので、実は真面目に式展開をして係数をまとめなくてもわかっちゃうよ、というツッコミも無しで…。
わかりやすい2自由度でもやってみる
基本に立ち返る事は意外と重要。教科書によく載っているわかりきった式で試してみましょう。本記事の冒頭に記載していた2自由度の式を使ったコードに書き換えた物を以下に示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
from sympy import* import numpy as np def generate_k_matrix(eq, x): K = Matrix(np.zeros((len(x), len(x)))) for i in range(len(eq)): for j in range(len(x)): K[i, j] = - expand(eq[i]).coeff(x[j]) return K # 変数リスト-------------------------------------------------------------------------------- # xの変数を定義 x1, x2 = symbols('x1 x2') x = [x1, x2] # kの変数を定義 k1, k2 = symbols('k1 k2') # aの変数を定義(今回使わないけど式の整合ののために定義) a1, a2 = symbols('a1 a2') # mの変数を定義(今回使わないけど式の整合ののために定義) m1, m2 = symbols('m1 m2') # fの変数を定義(今回使わないけど式の整合ののために定義) f1, f2 = symbols('f1 f2') # 運動方程式をモデルを読んだ通りに書く---------------------------------------------------------- e1 = f1 - k1 * x1 + k2 * (x2 - x1) - m1 * a1 e2 = f2 - k2 * (x2 - x1) eq = [e1, e2] # 剛性マトリクスを生成する関数を実行 K = generate_k_matrix(eq, x) print(K) |
以下が結果。教科書と同じになりました。
|
1 2 |
Matrix([[k1 + k2, -k2], [-k2, k2]]) |
まとめ
本記事ではまず前提知識として質点の振動系における運動方程式の書き方と、SymPyの過去記事を紹介し、連立運動方程式から剛性行列を算出するコードを書いてみました。
剛性行列を算出するのすら煩わしいと思ってしまう、超面倒くさがり屋さんのためのコードが出来てしまいました。おそらくこうしてさらに計算力が衰えてしまうのかも知れませんが、Python/SymPyの練習としては良かったと思います。
SymPyは僕らの見方!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント