
運動方程式を手計算で構築するのは大変です。自動的に式を導出することができれば、複雑なモデルでも手計算で間違う可能性が減ります。ここではsympy.physics.mechanicsでラグランジュ法を使った運動方程式の自動導出方法とシミュレーション方法を紹介します。
こんにちは。wat(@watlablog)です。運動方程式を自動導出するために、sympy.physics.mechanicsでラグランジュ法を使ってみます!
この記事のモチベーション
運動方程式を自動で導出したい(制御につなげたい)
WATLABブログでは過去「工学」カテゴリで運動方程式を立てて次の記事のようにシミュレーションをしていました。
・Pythonで多自由度振動系の過渡応答計算をする時はSciPyを使おう
この記事の内容でも運動方程式さえ立てれば容易にシミュレーションができますが、運動方程式を導出するのは問題によって結構面倒です。記事にあるような振動問題のみのモデルであればパターンが決まっているので簡単です。しかし、次のようなモデルはどうでしょうか?
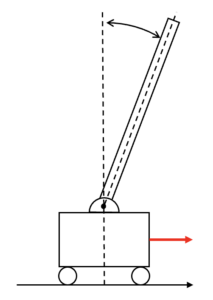
このモデルはカートと回転機構を持つ棒により構成された倒立振り子モデルです。棒はカート上の点を中心に自由に回転しますが、カートの動かし方を制御して棒を倒立させる制御問題によく使われます。制御問題の入門としてよくでてくるモデルですが、運動方程式は少し複雑です。
こういった問題を自由に扱えるようにしたいと思って調べていたときに、 sympy.physics.mechanicsの存在を知りました。このモジュールを使うと、適切な設定をすることで運動方程式を機械的に導出できます。
この記事では sympy.physics.mechanicsを試してみますが、まずは既にやったことのあるモデルを使ってこのモジュールに入門してみましょう。
動作環境
この記事のコードは以下の環境で動作確認をしています。こちらはmacOSですが、多分WindowsやLinuxでも問題なく動くでしょう。
| Mac | OS | macOS Sonoma 14.5 |
|---|---|---|
| チップ | Apple M3 | |
| CPU | 1.4[GHz] | |
| メモリ | 16[GB] |
| Python | Python 3.12.3 |
|---|---|
| sympy | 1.14.0 |
| numpy | 2.4.0 |
| scipy | 1.16.3 |
| matplotlib | 3.10.8 |
1自由度振動問題の運動方程式をsympyで導出する
モデルと答え
この章で扱うのは当ブログで何回も出てきた1自由度振動系モデルです。外力も作用していない減衰自由振動モデルを使ってコードを検証します。
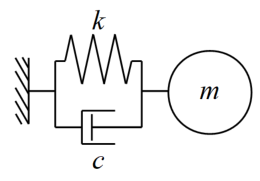
減衰自由振動モデルの運動方程式は式(1)で示されます。
式(1)は簡明なドット記法(またはニュートン記法)ですが、微分演算子記法(またはライプニッツ記法)で書くと式(2)になります。
それではここからはコードと数式を用いて sympy.physics.mechanicsを使っていきましょう。 .mechanicsにはラグランジュ法(Lagrangian method)とケイン法(Kane's method)の2通りの方法がありますが、ここではラグランジュ法の場合でコードを書いていきます。ラグランジュ法は解析力学の参考書の最初の章で出てくるような手法です。より詳しく知りたい方は解析力学の参考書を見てみましょう。
SymPyのimportとシンボル設定
まずはSymPyを
importして、必要なシンボル(式で使う文字)を設定します。ここで、
tと
m, c, kは
.symbolsで変数を表現していますが、
xは時間に依存するので
.dynamicsymbolsを使っており、ここでは一般化座標を意味します。
m, c, kは
positive=Trueとなっていますが、これは物理的に正の値しかとらないことをSymPyに宣言しているものです。多自由度を扱うときも同じで、質量や剛性マトリクスが正定値行列であることを強制します。こうすることで、SymPyの数式処理の結果で±表現や絶対値表現が多用されないシンプルな数式を出力できるようになります。
|
1 2 3 4 5 6 7 |
import sympy as sp import sympy.physics.mechanics as me # シンボル設定 t = sp.symbols('t') x = me.dynamicsymbols('x') m, c, k = sp.symbols('m c k', positive=True) |
座屈後のモデル等、実効的に負の剛性を考慮して不安定要素を入れるときは、 positive=Trueは外した方が良いでしょう。
力学モデルの定義
基準フレームの生成
続いて、今回のモデルの基準となる基底ベクトルの集合を次のコードで生成します。基底ベクトルの集合というのは3本の単位ベクトルを意味し、大きさ1で互いに直交するベクトルの集合です(式(3))。これを任意の名称で設定するフレームの中に生成するため、コード内では基準フレームの生成とコメントします。
|
1 2 |
# 基準フレームの生成 N = me.ReferenceFrame('N') |
フレーム毎にそれぞれ直交した基底ベクトルをつくることができるので、複数のフレーム間の回転等も扱えるようになります(今回の1自由度ではあまり恩恵はありませんが)。このフレームがないとそれらの処理を自分で書かないといけなくなります。
点と運動・拘束の関係を定義
今回のモデルは1自由度のばねマスダンパー系ですが、拘束部を点\(O\)、質点部を点\(P\)と考えましょう。
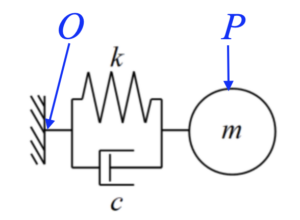
この点\(O\)と点\(P\)を .Pointを使ってコード上で定義し、それぞれの点の設定を行います。今回 .mechanicsでは「モデルを構築する」という感覚で運動方程式の導出を行います。
|
1 2 3 4 5 6 7 8 9 10 |
# O点(原点)とP点(質点)を定義 O = me.Point('O') P = me.Point('P') # O点はフレームNに対して速度0(固定) O.set_vel(N, 0) # P点はOに対しx方向(N.x)にxの位置・フレームNに対しxdotの速度 P.set_pos(O, x * N.x) P.set_vel(N, sp.diff(x, t) * N.x) |
O.set_vel(N, 0)とは、点\(O\)が先ほど定義したフレーム\(N\)に対して速度が0という内容を宣言しています。フレーム\(N\)は動く可能性がありますが、\(N\)が動いたとしても\(N\)に対する点\(O\)の速度は変わらず0という意味です。フレーム\(N\)に対して点\(O\)が拘束されていることを意味します。
P.set_pos(O, x * N.x)は、点\(P\)の位置が点\(O\)を基準にしていることと、その大きさがフレーム\(N\)の\(x\)方向(基底ベクトル
N.xの方向)に\(x\)であることを宣言しています。
P.set_vel(N, sp.diff(x, t) * N.x)は点\(P\)の速度に関する設定です。速度の大きさを時間微分で定義するので、観測者であるフレーム\(N\)を基準とします。
ラグランジュ法は位置や速度を基準フレームに対するベクトルの形で表現するので、このような書き方になります。
ラグランジアンの算出
ボディの定義
続いて .Particleで点\(P\)を参照し、質量\(m\)の物理的な点(ボディ)を作成します。先ほど点を定義した .Pointが幾何学的な情報を定義したのに対し、 .Particleは質量を設定して物理的な情報を定義します。 .Particleは内部で運動エネルギーを計算するので、ボディを使ってモデルを記述することで運動エネルギーの式を自分で書かなくてもよくなります。
|
1 2 |
# Bodyを定義 p = me.Particle('p', P, m) |
ちなみに、この点の運動エネルギー\(T\)は式(4)になります。
ポテンシャルエネルギー
ポテンシャルエネルギー\(V\)は式(5)を自分で記述します。今回のモデルはばねのひずみエネルギーがポテンシャルエネルギーに相当します。
|
1 2 |
# ポテンシャルエネルギー p.potential_energy = sp.Rational(1, 2) * k * x**2 |
ここで、 .Rational(1, 2)で\(\frac{1}{2}\)を表現しているのは厳密な割合を理論式としてSymPyに覚えさせるためです。数式で\(\frac{1}{2}\)や小数形式で\(0.5\)と記載すると、SymPyの数式処理が floatで処理する(以降の計算が数値近似になる)ことがあります。「数値計算ではなく理論式」である場合はこのような書き方をしましょう。書き方は複数あり、 from sympy import Sをしてから S(1)/2と書いてもOKです。
ラグランジアン
ラグランジュ法で運動方程式を導出するには、ラグランジアン(Lagrangian)を求める必要があります。ラグランジアン\(L\)は式(6)に示す通り、運動エネルギー\(T\)とポテンシャルエネルギー\(V\)の差で計算されます。
式(6)はコード上 .Lagrangianで計算します。運動エネルギーは座標系を指定しないと計算できないので、フレーム\(N\)を指定します。
|
1 2 |
# ラグランジアンを算出 L = me.Lagrangian(N, p) |
非保存力を定義
ラグランジュ法で運動方程式を求めるために、最後に非保存力を定義します。今回のモデルにおける非保存力は粘性減衰による力(式(7))です。
一般化座標を導入したのと同様に、力も一般化力として定義する必要がありますが、今回のモデルは一般化力\(Q\)も式(7)と同じです(式(8))。※\(\mathbf{r}\)は位置ベクトル。
コードでは次のように書きます。今回は1つだけですが、一般化力はすべての力を足し合わせる必要があるため、力を作用点毎のリスト形式で与えます。
|
1 2 |
# 非保存力 forcelist = [(P, -c * sp.diff(x, t) * N.x)] |
運動方程式の導出
ここまでで準備は完了です。Python/SymPyによる運動方程式の導出はこの後すぐできてしまいますが、ここで一度ラグランジュ法が何をしているかを説明しておきます。
ラグランジアンは式(6)で計算されるため、式(4)と式(5)を使って式(9)となります。
ラグランジュ方程式の一般形は式(10)で表されます。ここに先ほどのラグランジアン\(L\)と一般化力\(Q\)(式(8))を代入して計算を進めれば、今回設定したモデルの運動方程式が自然と導出されます。
このラグランジュ方程式は一般形なので、解析対象のモデルが変わってもラグランジアン\(L\)と一般化力\(Q\)を求めることができれば全く同じ形の方程式でそれぞれの運動方程式を導出できます。
式(10)に\(L\)と\(Q\)を代入し、式(11)と計算を進めてみます。左辺第1項の括弧内は速度\(\dot{x}\)による偏微分であるため、ラグランジアンの変位項は定数とみなし\(m \dot{x}\)のみ残ります。同様に、左辺第2項は変位\(x\)による偏微分であるため、\(kx\)が残ります。さらに時間微分を進め、移行をして右辺を0にすることで、正解の運動方程式(1)を得ることができました。
それではPython/SymPyのコードを仕上げます。次の .LagrangesMethodでラグランジュ法を使った運動方程式を導出します。 .LagrangesMethodでは基準とするフレームを1つ選択します。 .simplifyは今回は効果がないですが、複雑なモデルの運動方程式を導出した際に、物理的な意味を変更せずシンプルな形に整形してくれるのでおすすめです。 pprint関数は数式をASCIIアート的に綺麗に表示する機能を持ちます。
|
1 2 3 4 5 6 |
# ラグランジュ法による運動方程式の導出 LM = me.LagrangesMethod(L, [x], forcelist=forcelist, frame=N) eom = sp.simplify(LM.form_lagranges_equations()) # 結果出力 sp.pprint(eom) |
コードを実行すると、次の結果が出力ウィンドウに表示されます。ちょっと表示が崩れているような気がしますが、=0の場合の左辺が書かれています。この記法は式(2)のライプニッツ記法ですね。
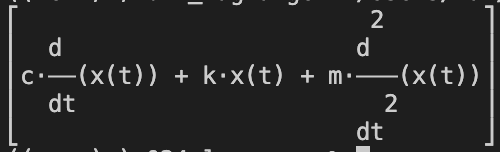
運動方程式を導出する全コード
ここまでの全コードをこちらに置いておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 |
import sympy as sp import sympy.physics.mechanics as me # シンボル設定 t = sp.symbols('t') x = me.dynamicsymbols('x') m, c, k = sp.symbols('m c k', positive=True) # 基準フレームの生成 N = me.ReferenceFrame('N') # O点(原点)とP点(質点)を定義 O = me.Point('O') P = me.Point('P') # O点はフレームNに対して速度0(固定) O.set_vel(N, 0) # P点はOに対しx方向(N.x)にxの位置・フレームNに対しxdotの速度 P.set_pos(O, x * N.x) P.set_vel(N, sp.diff(x, t) * N.x) # Bodyを定義 p = me.Particle('p', P, m) # ポテンシャルエネルギー p.potential_energy = sp.Rational(1, 2) * k * x**2 # ラグランジアンを算出 L = me.Lagrangian(N, p) # 非保存力 forcelist = [(P, -c * sp.diff(x, t) * N.x)] # ラグランジュ法による運動方程式の導出 LM = me.LagrangesMethod(L, [x], forcelist=forcelist, frame=N) eom = sp.simplify(LM.form_lagranges_equations()) # 結果出力 sp.pprint(eom) |
SymPyで導出した運動方程式を使ってシミュレーションする
導出した式をそのまま使ってシミュレーション、matplotlibで結果を出力するコードを紹介します。
これまでWATLABブログでは以下の記事のようにSciPyの
odeintによるシミュレーションを行ってきました。
・Pythonで多自由度振動系の過渡応答計算をする時はSciPyを使おう
この記事では odeintより新しい solve_ivpを使ったシミュレーション方法を紹介します。この記事では直接使いませんが、 odeintではできなかったイベント検知機能があったり、 odeintからかなりアップデートがされているようです。それではシミュレーションをしましょう。
状態方程式への変換
状態変数を準備
ラグランジュ法で得られた運動方程式(11)は2階の常微分方程式です。 odeintと同様に solve_ivpも1階の常微分方程式しか解けないので、1階化として状態方程式に変換します。
当ブログでも普段から実施していますが、式(12)の関係を使うことで状態変数を定義します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import sympy as sp import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp 〜省略〜 # ----シミュレーション---- # 運動方程式から左辺の式を取り出す expr = sp.simplify(eom[0]) # 状態方程式化のために状態変数を準備 xd = sp.diff(x, t) xdd = sp.diff(x, t, 2) |
運動方程式を\(\ddot{x}\)について解く
続いて式(11)の最終式を\(\ddot{x}\)について解いて式(13)を得ます。
コードにするとこちらです。
|
1 2 3 4 |
# 運動方程式をxddについて解く xdd_expr = sp.solve(sp.Eq(expr, 0), xdd)[0] print("\nSolved for xdd:") sp.pprint(xdd_expr) |
これで状態方程式(14)が完成します。
記号式を数値計算用の関数に変換
solve_ivpを使うために、 .lamdifyを使って記号式を数値計算用の関数に変換します。
|
1 2 3 |
# 記号式を数値計算用の関数に変換 X, XD = sp.symbols('X XD', real=True) xdd_func = sp.lambdify((X, XD, m, c, k), xdd_expr.subs({x: X, xd: XD}), "numpy") |
数値計算
数値計算部分はこちらです。 def rhsは状態方程式の右辺を返す関数です。初期条件として初期変位と初期速度を与えて solve_ivpで数値計算をします。ちなみにivpとは、IVP : Initial Value Problem(初期値問題)です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# パラメータと初期条件 m_val = 1.0 c_val = 0.2 k_val = 20.0 x0 = 0.1 # 初期変位 [m] xd0 = 0.0 # 初期速度 [m/s] y0 = [x0, xd0] # 常微分方程式 def rhs(t_num, y): x_num, xd_num = y xdd_num = xdd_func(x_num, xd_num, m_val, c_val, k_val) return [xd_num, xdd_num] # 時間積分 t0, t1, dt = 0.0, 100.0, 0.001 t_eval = np.arange(t0, t1, dt) sol = solve_ivp(rhs, (t0, t1), y0, t_eval=t_eval, rtol=1e-9, atol=1e-12) |
プロットまで含めた全コードと実行結果
運動方程式から数値計算まで、そのまま実行できる全コードをこちらに示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 |
import sympy as sp import sympy.physics.mechanics as me import numpy as np import matplotlib.pyplot as plt from scipy.integrate import solve_ivp # シンボル設定 t = sp.symbols('t') x = me.dynamicsymbols('x') m, c, k = sp.symbols('m c k', positive=True) # 基準フレームの生成 N = me.ReferenceFrame('N') # O点(原点)とP点(質点)を定義 O = me.Point('O') P = me.Point('P') # O点はフレームNに対して速度0(固定) O.set_vel(N, 0) # P点はOに対しx方向(N.x)にxの位置・フレームNに対しxdotの速度 P.set_pos(O, x * N.x) P.set_vel(N, sp.diff(x, t) * N.x) # Bodyを定義 p = me.Particle('p', P, m) # ポテンシャルエネルギー p.potential_energy = sp.Rational(1, 2) * k * x**2 # ラグランジアンを算出 L = me.Lagrangian(N, p) # 非保存力 forcelist = [(P, -c * sp.diff(x, t) * N.x)] # ラグランジュ法による運動方程式の導出 LM = me.LagrangesMethod(L, [x], forcelist=forcelist, frame=N) eom = sp.simplify(LM.form_lagranges_equations()) # 結果出力 sp.pprint(eom) # ----シミュレーション---- # 運動方程式から左辺の式を取り出す expr = sp.simplify(eom[0]) # 状態方程式化のために状態変数を準備 xd = sp.diff(x, t) xdd = sp.diff(x, t, 2) # 運動方程式をxddについて解く xdd_expr = sp.solve(sp.Eq(expr, 0), xdd)[0] print("\nSolved for xdd:") sp.pprint(xdd_expr) # 記号式を数値計算用の関数に変換 X, XD = sp.symbols('X XD', real=True) xdd_func = sp.lambdify((X, XD, m, c, k), xdd_expr.subs({x: X, xd: XD}), "numpy") # パラメータと初期条件 m_val = 1.0 c_val = 0.2 k_val = 20.0 x0 = 0.1 # 初期変位 [m] xd0 = 0.0 # 初期速度 [m/s] y0 = [x0, xd0] # 常微分方程式 def rhs(t_num, y): x_num, xd_num = y xdd_num = xdd_func(x_num, xd_num, m_val, c_val, k_val) return [xd_num, xdd_num] # 時間積分 t0, t1, dt = 0.0, 100.0, 0.001 t_eval = np.arange(t0, t1, dt) sol = solve_ivp(rhs, (t0, t1), y0, t_eval=t_eval, rtol=1e-9, atol=1e-12) # プロット plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' fig = plt.figure() ax1 = fig.add_subplot(111) ax1.xaxis.set_ticks_position('both') ax1.yaxis.set_ticks_position('both') ax1.plot(sol.t, sol.y[0], label="x(t)") ax1.set_xlabel("Time[s]") ax1.set_ylabel("Disp.[m]") ax1.legend() fig.tight_layout() plt.show() |
コードを実行すると次のmatplotlibの図が表示されます。減衰振動の挙動が確認されました。
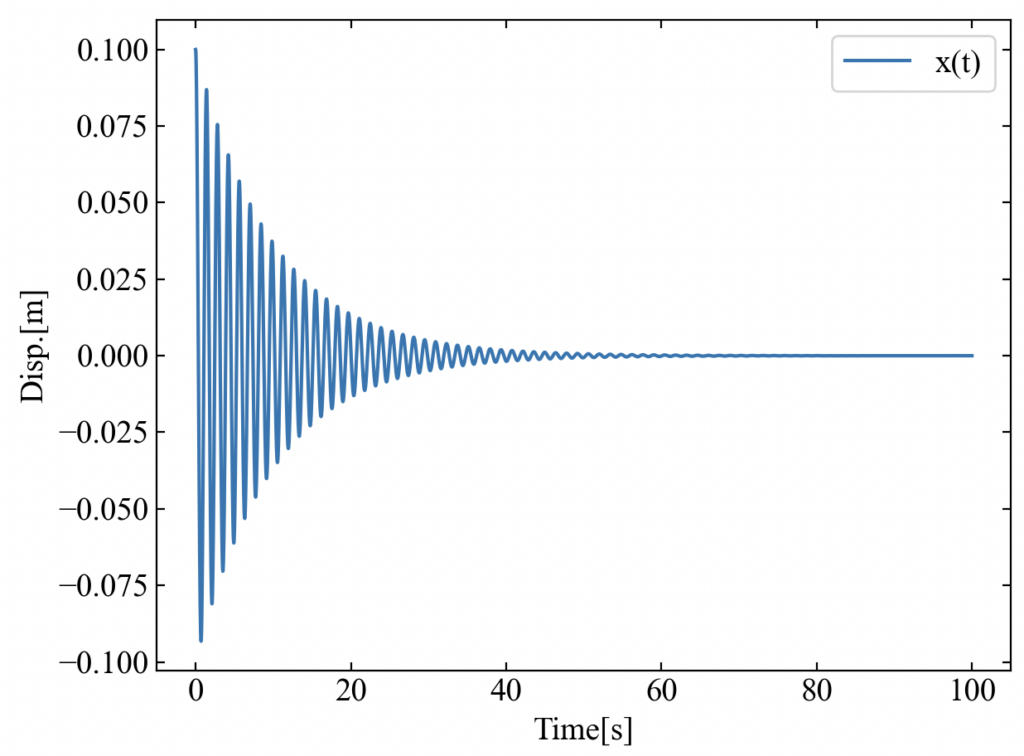
まとめ
この記事では sympy.physics.mechanicsを使って運動方程式を導出する方法についてまとめました。今回は運動エネルギーとポテンシャルエネルギーをラグランジュ方程式に代入して運動方程式を求めるラグランジュ法を紹介しています。ポテンシャルエネルギーと非保存力を自分で書く必要はありますが、1つずつ力の関係を自分で求める場合よりもかなり機械的に運動方程式を導出できたのではないかと思います(解析力学すごい)。
解析力学の手法であるラグランジュ方程式を使ってみました!
Xでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!