
Pythonのscipy.integrate.quadやscipy.integrate.dblquadを使えば簡単に数値積分ができますが、当然結果はシンプルに積分値が返ってくるだけです。ここでは他者へ説明する目的で基本的な1重積分をはじめ、2重積分までのmatplotlibによる可視化方法を紹介します。
こんにちは。wat(@watlablog)です。今回は積分の可視化をテーマにscipy.integrateを使ってみます!
本記事の目標
積分結果を可視化する
曲線を積分すると面積を、曲面を2重積分すると体積を求めることができます。
一般的に積分がどのような処理を行っているかを他者へ説明する時、下図に示すような、関数と求積した部分を共にプロットするのではないでしょうか。
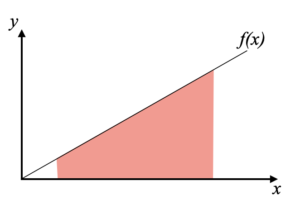
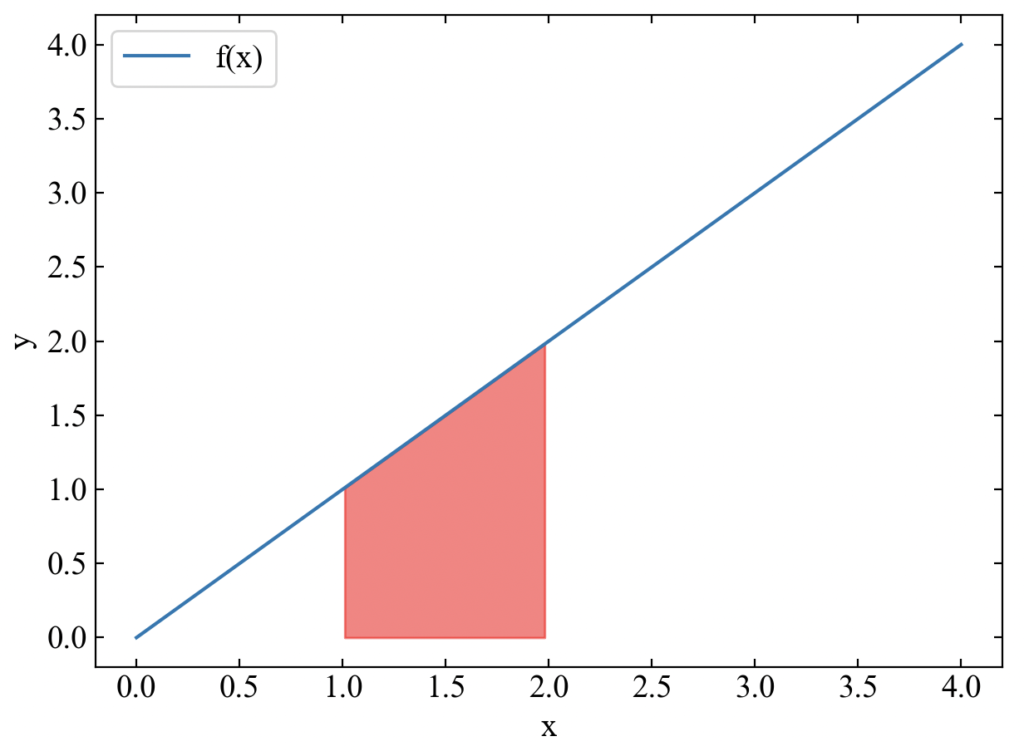
今回はPythonのscipy.integrateによる積分方法を確認すると共に、matplotlibによる可視化例を得るところまでを扱います。まず初めに上図と同様の最も簡単な1変数関数の1重積分を扱い、以下の結果を出すコードを書きます。
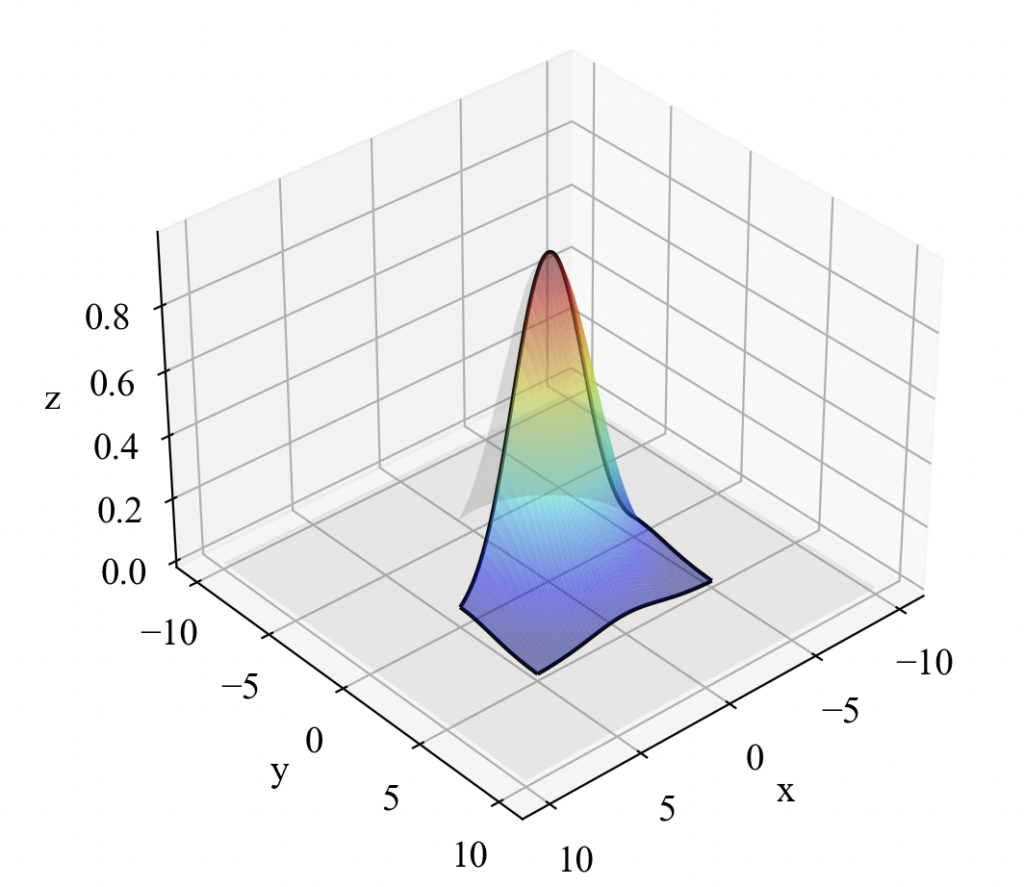
次に曲面を2重積分して体積を求める問題に対し、色々な関数で可視化を試してみます。可視化の方法は色々あれど、下図のようなアウトプットを出すコードを紹介します。これはガウス関数の2重積分区間に色付けしたり、区間がわかりやすくなるように黒いエッジをつけているものです。
それでは早速コードを書いてみましょう!
関連記事
Pythonによる積分は以下の記事も参考にしてください。
・Pythonでルジャンドル多項式を使ってガウス積分をする方法
・積分で解くWi-FiパスワードをPython/sympyで計算する
動作環境
この記事のコードは以下のPython環境で動作を確認しました。
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.23.0 |
| Scipy | 1.4.1 |
| matplotlib | 3.7.1 |
1重積分の可視化を行うPythonコード
まずは最も簡単な式(1)を使って積分と可視化を行ってみましょう。
scipyのintegrateからquadをimportすることで積分を行います。関数fを定義しておき、積分区間a, bを使ってquad(f, a, b)と書くことで求積が可能です。
積分結果の可視化は.fill_betweenで行っています。1重積分の可視化はこれ一択だと思いました。
scipy.integrate.quadの公式ドキュメント:https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.quad.html
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 |
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import quad def f(x): """ 被積分関数 """ y = x return y def plot(x, y, a, b, result): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データをプロットする。 label_text = "$\int_{{a}}^{{b}} f(x) \, dx = $" + str(result) ax1.plot(x, y, label=label_text) ax1.fill_between(x, y, where=[a <= xi <= b for xi in x], color='red', alpha=0.5) ax1.legend(loc='upper left') # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # 積分:x ∈ [a, b] a, b = 1, 2 result, _ = quad(f, a, b) print('Quadrature result=', result) # グラフの描画 x = np.linspace(0, 4, 100) y = f(x) plot(x, y, a, b, result) |
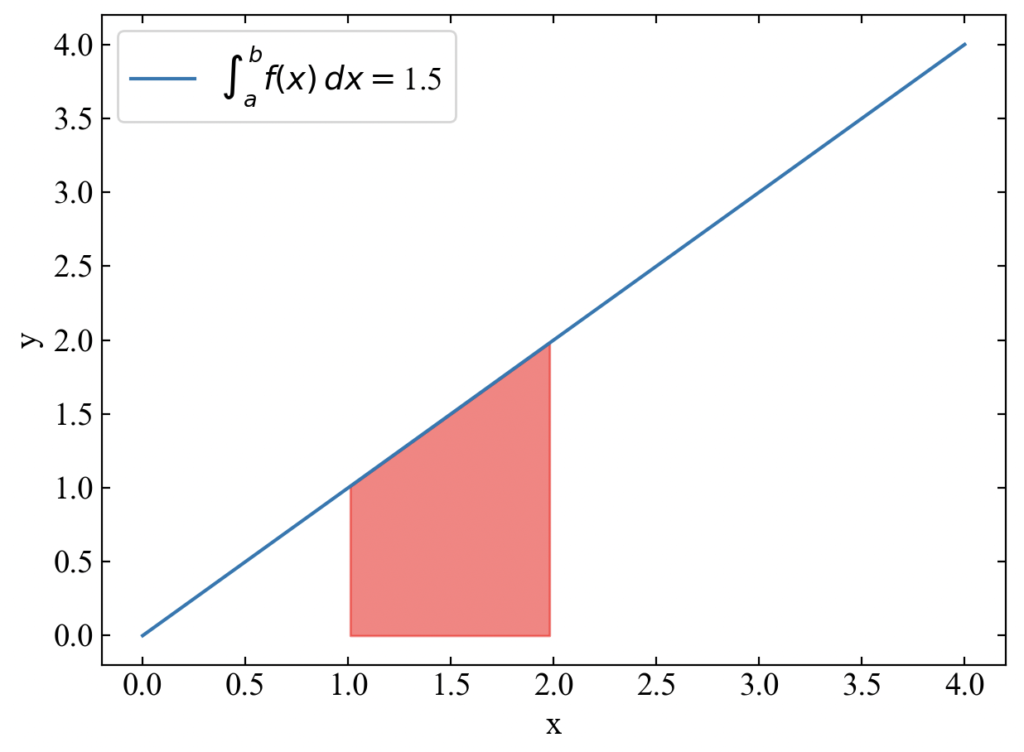
結果はこちら。出力ウィンドウにもquadの結果が書かれていますが、labelにも載せるようにしてみました。手計算してみるとわかりますが、quadの数値1.5は正解です(この積分は暗算でもできますね)。
次はもう少し変曲点が多くて面白い関数として、式(2)で試してみましょう。
関数fの部分と、積分区間a, bを変更します。
|
1 2 3 4 5 6 7 8 9 |
def f(x): """ 被積分関数 """ y = x ** 4 - 10 * x ** 3 + 25 * x ** 2 return y # 積分:x ∈ [a, b] a, b = 2, 3 |
こちらが結果です。式を変更するだけで正常に機能していることがわかりました。
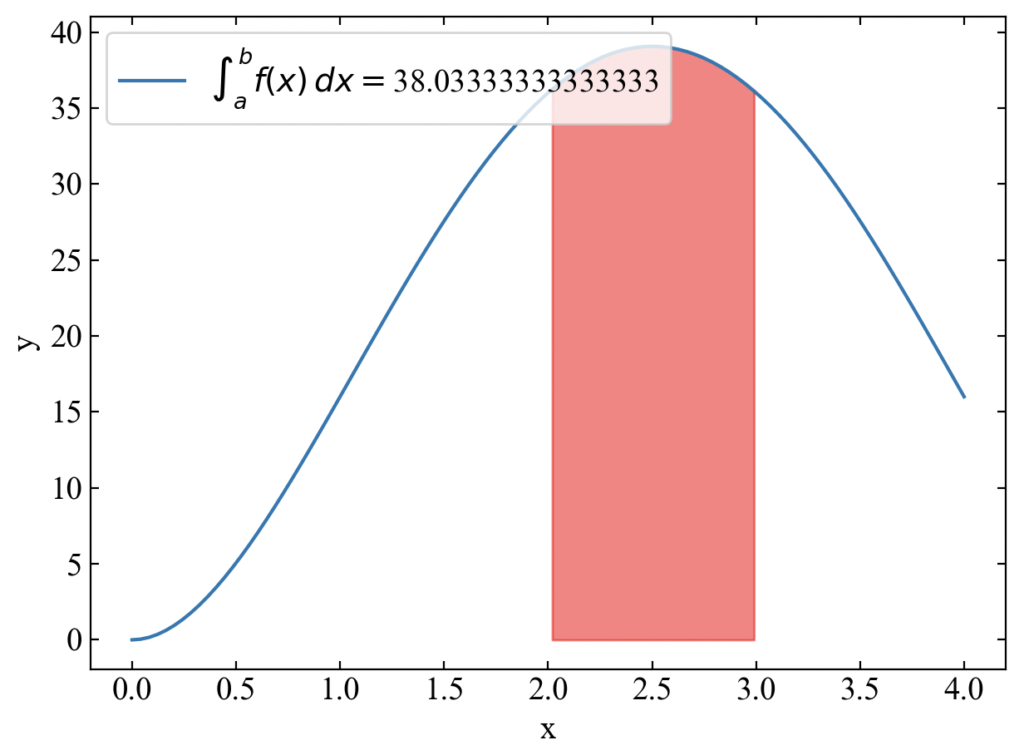
これで1重積分の計算方法や可視化方法はわかったので、次に進みましょう。
2重積分の可視化を行うPythonコード
次は式(3)の2重積分を行います。式(3)は平面の方程式です。ここで\(w_{0}=1, w_{1}=1, w_{2}=1\)とします。
コードはこちら。2重積分はscipy.integrate.dblquadを使います(double quadratureという意味らしい)。2重積分の可視化は色々試行錯誤しましたが、積分区間を黒いエッジで囲い、面にカラーマップを貼るという見せ方が最も美しいとの結論に達しました(個人の感想です)。
scipy.integrate.dblquadの公式ドキュメント:https://docs.scipy.org/doc/scipy/reference/generated/scipy.integrate.dblquad.html
積分区間をエッジで囲うために.plot_wireframeを使っていますが、これだけだと細かい線が多数表示されるためrstrideとcstrideを使ってメッシュの間隔を大きくする工夫をしました。
また本筋とは関係ないですが、*x_range_integrateとアスタリスクをつけて引数を渡すことで一つずつ記載しなくて良いという小ワザも使ってみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 |
import numpy as np import matplotlib.pyplot as plt from scipy.integrate import dblquad def f(x, y): """ 被積分関数 """ w0 = 1 w1 = 1 w2 = 1 z = w0 + w1 * x + w2 * y return z def plot(x_vals, y_vals, z_vals, x_vals_integrate, y_vals_integrate, z_vals_integrate, result): """ グラフ描画する関数 """ # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') # データをプロットする。 # 被積分関数 label_text = "$\int_{{a}}^{{b}}\int_{{c}}^{{d}} f(x, y) \, dydx = $" + str(result) ax1.plot_wireframe(x_vals, y_vals, z_vals, alpha=0.2, edgecolor='gray') # 積分区間の面 ax1.plot_wireframe(x_vals_integrate, y_vals_integrate, z_vals_integrate, rstride=99, cstride=99, color='black', label=label_text) ax1.plot_surface(x_vals_integrate, y_vals_integrate, z_vals_integrate, cmap='jet', alpha=0.5) # グラフを表示する。 ax1.legend() fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # 描画の範囲を定義 x_range = [-10, 10] y_range = [-10, 10] # 積分の範囲を定義 a, b = 0, 5 c, d = -5, 5 x_range_integrate = [a, b] y_range_integrate = [c, d] # 積分:x ∈ [a, b], y ∈ [c, d] result, _ = dblquad(f, a, b, c, d) print('Quadrature result=', result) # グリッドを生成 x_vals, y_vals = np.meshgrid(np.linspace(*x_range, 100), np.linspace(*y_range, 100)) x_vals_integrate, y_vals_integrate = np.meshgrid(np.linspace(*x_range_integrate, 100), np.linspace(*y_range_integrate, 100)) # zの値を計算 z_vals = f(x_vals, y_vals) z_vals_integrate = f(x_vals_integrate, y_vals_integrate) # 可視化 plot(x_vals, y_vals, z_vals, x_vals_integrate, y_vals_integrate, z_vals_integrate, result) |
結果がこちら。3次元プロットはやはり映えますね。積分結果は175(数値積分なのでピッタリいかない)となりました。果たしてこの結果は合っているのでしょうか?2重積分の暗算は少々やっかいなので計算してみましょう。
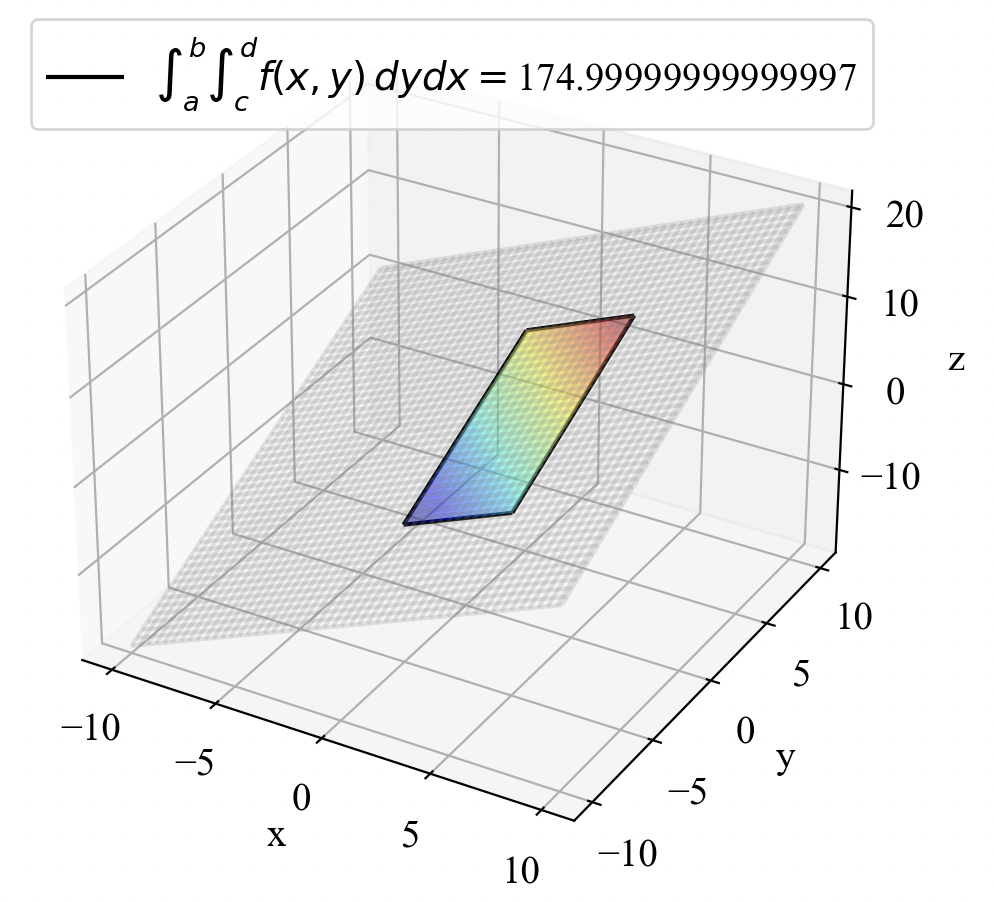
積分は加算に関して線形であるため、3つの積分に分解できます。3つ目の項は奇関数であるため0になり簡単になるため、式(4)のように展開して答えは175を得ました。プログラムは正しく動作しているようですね。
自分でプログラムを書いた時は、手計算でも簡単に答えが出る問題を解いて検証することが重要です!今回のケースだとxとyの範囲を逆にしてしまうバグもあるあるです。
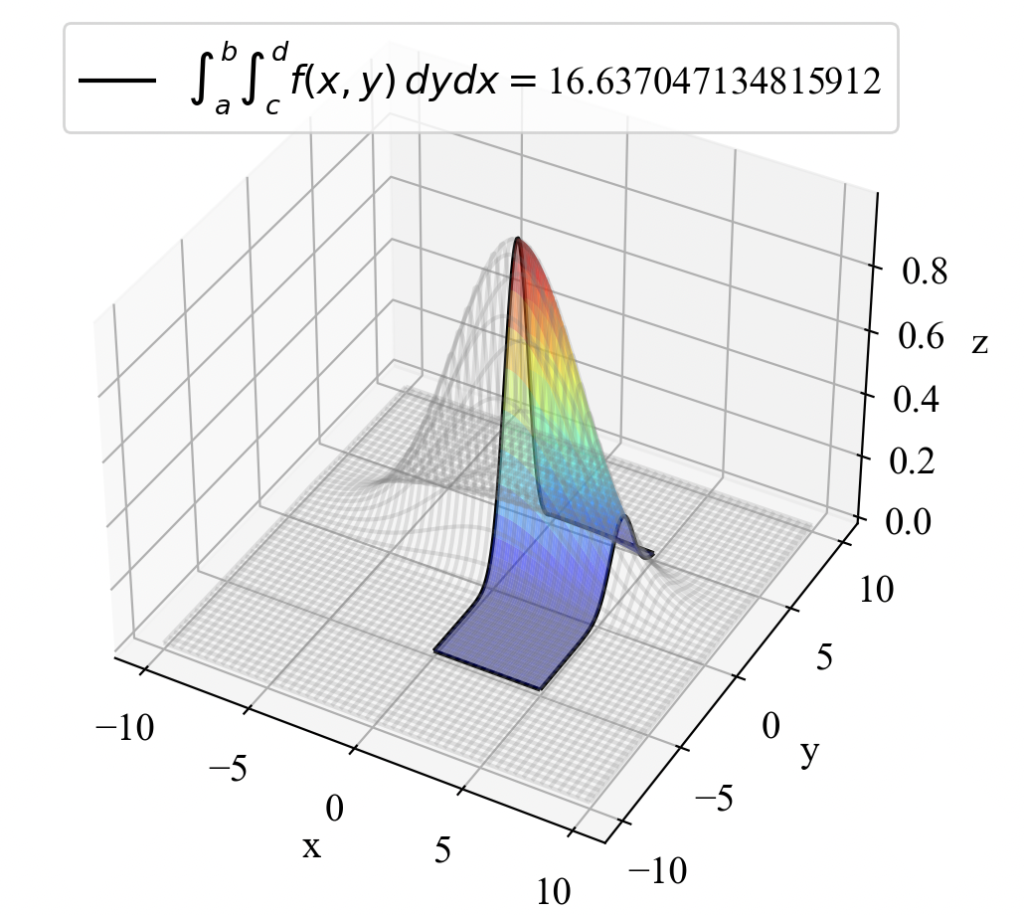
次は式(5)で示す2次元のガウス関数です。2次元ガウス関数は様々な用途で用いられるので、これも2重積分してみましょう。
Pythonコードで変更するのは関数部分のみです。積分範囲は先ほどと同様にしました。
|
1 2 3 4 5 6 7 8 9 10 11 |
def f(x, y): """ 被積分関数 """ mu_x = 0 mu_y = 2 sigma_x = 3 sigma_y = 1 z = np.exp(-(x - mu_x) ** 2 / (2 * sigma_x ** 2)) * np.exp(-(y - mu_y) ** 2 / (2 * sigma_y ** 2)) return z |
結果がこちら。綺麗ですね。ガウス関数は天文学であれば星の光強度、工学であればベクトルデータのヒストグラムといった用途で2重積分の需要がありそうです。
まとめ
この記事ではscipy.integrate.quadやdblquadを使った積分方法を紹介しました。それだけだと類似の記事がたくさんあったので、このブログでは主に可視化に特化してみました。
積分結果を得るだけなら可視化は全く必要ありませんが、結果を他者へ説明したり理解を深めたりする時には有用だと思います。
今回は積分区間が定数の問題のみを扱いましたが、世の中には積分区間にxやyが含まれる問題もあります。次回はそのような一歩進んだ問題の可視化もトライしてみたいと思いました。
基本的な積分を求めるPythonコードが書けました!
X(旧Twitter)でも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!