
PythonにはNumPyやSciPyによる優秀な高速フーリエ変換(FFT)アルゴリズムがありますが、基本的なFFTの仕組みを学習するにもPythonは最適です。ここでは最も一般的なFFTアルゴリズムであるCooley-Tukey法をPythonのNumPyで記述し、numpy.fftの結果と比較します。さらに、データ点が2の冪乗でない場合のゼロパディング処理も実装します。
こんにちは。wat(@watlablog)です。ここではCooley-Tukey法による高速フーリエ変換をPythonで書き、そのアルゴリズムを勉強します!
DFTとFFTの違い
DFT:離散フーリエ変換
WATLABブログでは以下の記事で離散フーリエ変換(DFT:Discrete Fourier Transform)を紹介しました。
・Pythonで検証しながらSwiftで離散フーリエ変換を実装する
この記事では基本的なDFTの式とPythonやSwiftによる実装例を紹介しましたが、「実用的ではない」と結論付けています。その理由はDFTの計算量が\(O(N^{2})\)とデータ数の二乗に比例して膨大な計算が必要になってしまうことにあります。
プログラム的にはとても簡単に書けてしまいますが、音声データ処理といったkHzオーダーのサンプリングレートを持つデータの処理をしようとすると一般のPCではかなり長い時間待たされてしまうことでしょう。
その計算量に関する問題を改善するために、高速フーリエ変換が考案されました。
FFT:高速フーリエ変換
FFTの特徴
高速フーリエ変換(FFT:Fast Fourier Transform)とは、離散フーリエ変換(DFT)を高速に計算するために考案された手法です。
線形かつ周期的なデータである必要はありますが、その計算量は\(O(N \log N)\)になるためデータが膨大になるに従いDFTと比べものにならないくらいの計算速度改善を実感します。
Cooley-Tukey法
FFTの一般的なアルゴリズムにCooley-Tukey法があります。この手法は問題をより小さな部分問題に分解する「分割統治」戦略をとっています。
アルゴリズムは①データの分割→②再帰的なDFT→③データの結合(バタフライ演算)の順番で計算を行うのが特徴です。
数式による説明は英語版のWikipedia\(^{[1]}\)がわかりやすいと思います。
筆者はそんなに詳しく説明できないですが、要は重複計算をしてしまうDFTを最適化して効率良く必要な計算のみしていこうという方針のようです。単純に計算数を少なくすることで高速化しています。
この記事では代表的なFFTアルゴリズムであるCooley-Tukey法をPythonでコーディングして結果を確認します。ただし筆者も勉強中であり学習的な用途で書いたものなので、この記事のコードは計算高速性について最適化されたものではありません。
FFTは高速性を求めると非常に奥が深い計算です。必要であれば他の研究者のコードや安定したライブラリを使いましょう。
ちなみにPythonライブラリを多用したコードは以下の記事をご覧ください。
・PythonでFFT実装!SciPyのフーリエ変換まとめ
・ただPythonでcsvから離散フーリエ変換をするだけのコード
動作環境
この記事のコードは以下の環境で実行しました。
PC
■Mac
| Mac | OS | macOS Ventura 13.2.1 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
Python
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
Cooley-Tukey法によるFFTコード
データ長が2の冪乗の場合
関数部のPythonコード
以下にCooley-Tukey法で書いたFFTのPython関数を示します。標本点数が1になるまで再帰的に同じ関数を使い続ける構造となっていることがわかると思います。
再帰的な処理はプログラミングでよく出てきますが、WATLABブログでは基本情報技術者試験の勉強をした時にマージソートの記事で説明しましたので参考にしてみてください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 |
def fft(x): """ FFT Cooley-Tukey Method """ # 標本点数 N = x.shape[0] # Nが1なら、そのままxを返す if N == 1: return x # ビット反転順序に基づいて、偶数インデックスと奇数インデックスの部分配列を得る even = fft(x[::2]) odd = fft(x[1::2]) # DFTの結果を格納するための複素数配列 T = np.exp(-2j * np.pi * np.arange(N) / N) # 偶数部分と奇数部分のDFTを組み合わせる(バタフライ演算) F = np.concatenate([even + T[:N // 2] * odd, even + T[N // 2:] * odd]) return F |
この関数はデータ長が2の冪乗(2, 4, 6, 16, 32, 64, 128, 256, 512, 1024, 2048, 4096, 8192, 16384, 32768…)である場合のみ使用できます。これはデータをevenとoddに再帰的な分割をしていることから来る制約です。
結果評価までのサンプルコード(コピペ動作OK)
下のコードはコピペで動作するサンプルコードです。sample_wave()関数でデータポイントを指定した直流成分付き正弦波を生成し、自作のDFTと自作のFFT(上記関数)、numpy.fftを計算して計算時間を確認します。自作のFFTは再帰的処理をしている都合、振幅計算はfft_post()で行い、その結果をmatplotlibで表示させます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 |
import numpy as np from matplotlib import pyplot as plt import time def fft(x): """ 高速フーリエ変換(FFT):Cooley-Tukey法 """ # 標本点数 N = x.shape[0] # Nが1なら、そのままxを返す if N == 1: return x # ビット反転順序に基づいて、偶数インデックスと奇数インデックスの部分配列を得る even = fft(x[::2]) odd = fft(x[1::2]) # DFTの結果を格納するための複素数配列 T = np.exp(-2j * np.pi * np.arange(N) / N) # 偶数部分と奇数部分のDFTを組み合わせる(バタフライ演算) F = np.concatenate([even + T[:N // 2] * odd, even + T[N // 2:] * odd]) return F def dft(t, x): """ 離散フーリエ変換(DFT) """ # N:データ点数、F:フーリエスペクトル(複素数)、dt:時間刻み[s]、freq:周波数軸 N = len(x) F = np.zeros(N, dtype=complex) dt = t[1] - t[0] freq = np.zeros(N, dtype=float) amp = np.zeros(N, dtype=float) # 離散フーリエ変換式と周波数軸の式 for k in range(N): for n in range(N): # フーリエスペクトル F[k] += x[n] * np.exp(-2j * np.pi * n * k / N) # 周波数軸 freq[k] = k / (N * dt) # 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)でスケーリング係数を変える。 if k == 0: sf = N else: sf = N / 2 # 振幅 amp[k] = np.sqrt(F[k].real ** 2 + F[k].imag ** 2) / sf return freq, amp def fft_post(t, F): """ FFT結果から周波数軸と振幅成分を計算する """ N = len(F) dt = t[1] - t[0] freq = np.zeros(N, dtype=float) amp = np.zeros(N, dtype=float) for k in range(N): # 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)でスケーリング係数を変える。 if k == 0: sf = N else: sf = N / 2 # 振幅 amp[k] = np.sqrt(F[k].real ** 2 + F[k].imag ** 2) / sf # 周波数軸 freq[k] = k / (N * dt) return freq, amp def sample_wave(): """ サンプル波形 """ # A:変動成分振幅、f:周波数[Hz]、dc:直流成分、N:標本点数 A = 1 f = 10 dc = 1 N = 512 # サンプル波形。t:時間軸[s]、x:時間信号 t = np.linspace(0, 5, N) x = A * np.sin(2 * np.pi * f * t) + dc return t, x def plot(t, x, freq, amp): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(7, 5)) ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x') ax2.set_xlabel('Frequency[Hz]') ax2.set_ylabel('x') # スケールの設定をする。 #ax2.set_xlim(0.0, 20.0) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='time', lw=1, color='red') ax2.plot(freq, amp, label='freq', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' t, x = sample_wave() # 自作DFT t0 = time.time() DFT = dft(t, x) t1 = time.time() print('DFT time=', t1 - t0, '[s]') # 自作FFT t0 = time.time() F = fft(x) t1 = time.time() print('FFT time=', t1 - t0, '[s]') # NumPyのFFT t0 = time.time() F_numpy = np.fft.fft(x) t1 = time.time() print('numpy.fft time=', t1 - t0, '[s]') # numpy.fftと比較 print('Comparison between zisaku and numpy=', np.allclose(F, F_numpy)) # 周波数軸、振幅計算と結果の可視化 freq, amp = fft_post(t, F) plot(t, x, freq, amp) |
実行結果:計算速度とnumpy.fftとの比較検証
プログラムを実行するとコンソールには各手法の計算時間が表示されます。今回は512データポイントの場合ですが、自作DFTが0.55[s]、自作FFTが0.0098[s]、numpy.fftが0.00095[s]という結果でした。
numpyが圧倒的に高速なのはさすがですが、自作FFTも自作DFTより数十倍も速くなっています。
|
1 2 3 4 |
DFT time= 0.5485739707946777 [s] FFT time= 0.009795904159545898 [s] numpy.fft time= 0.0009510517120361328 [s] Comparison between zisaku and numpy= True |
コードの最後で「np.allclose(F, F_numpy)」を使って自作FFTとnumpy.fftの結果を比較しています。np.allcloseは全ての要素が一致している場合Trueを返しますが、先ほどの結果もTrueになっており自作したFFTとnumpy.fftの結果が一致していることを確認しました。
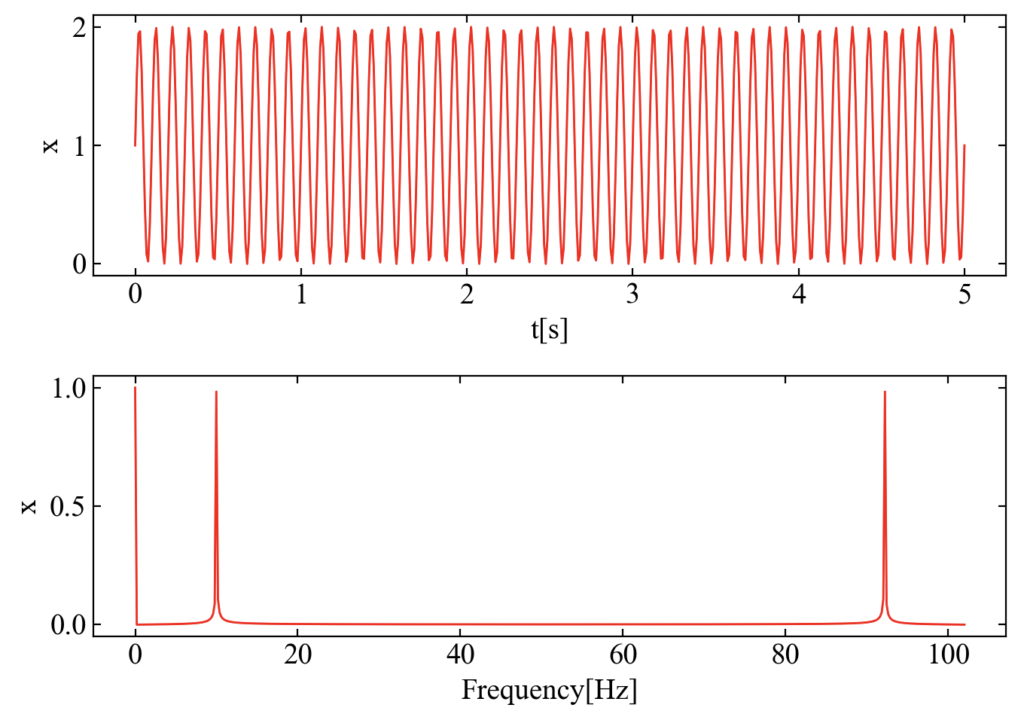
実行結果:時間波形と周波数波形
下図がグラフです。周波数波形には鏡像ピークが出ていますが、これが正常です。通常振幅評価をする時はナイキスト周波数で表示を切るのが一般的ですが、今回は全体を俯瞰して検証する目的でそのまま表示させています。
fft_post()でスケーリング係数sfを分岐してかけていますが、この操作のおかげで直流成分も指定した数値となっていることも確認できました。この辺の話は以下の記事に書いた通りです。
・Pythonで検証しながらSwiftで離散フーリエ変換を実装する
データサンプル数と計算時間の関係
DFTとFFTを比較するなら、やはりデータサンプル数と計算時間の関係をプロットしたくなります!こちらがその結果です。
音声データの周波数分析はフレームサイズが2048より大きく、さらにオーバーラップで何回も計算することを考えるとFFTを使わない手はないというほどの差ですね…。
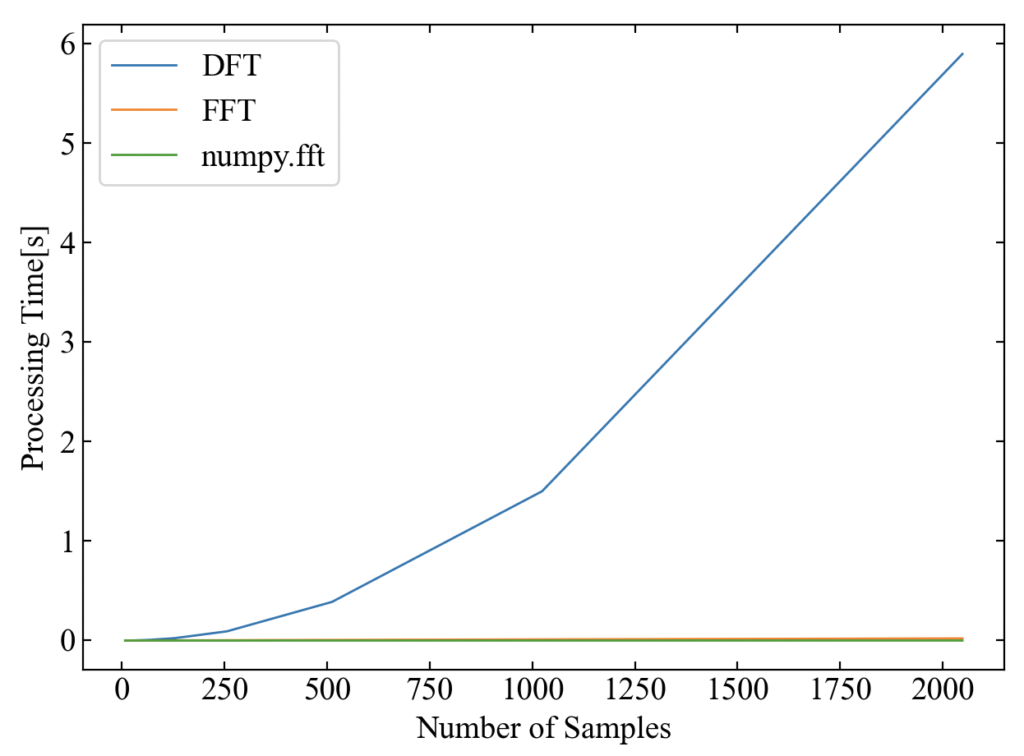
自作FFTもかなり良い…と思いきや、numpy.fftはさすがの計算速度!素直にnumpyやscipyを使いましょう。
Pythonでは素直にnumpyやscipyを使いましょう(もう一回言っておきます)。
ただし、ライブラリが使えない状況(Excel VBAやその他言語)の場合は一度フルスクラッチしておけばいつでも使える状態になるので、このようなコードの写経はしておいた方が良いと思いました!
データ長が2の冪乗でない場合:ゼロパディング法
ゼロパディングとは?
Cooley-Tukey法ではデータ長が2の冪乗数である必要がありましたが、その制約を取ることも可能です。
ゼロパディングを行うことでそれを実現しますが、ゼロパディングについては過去WATLABブログでも周波数分解能を操作する時に使ったことがあります。詳細は以下の記事をご確認ください。
・ゼロパディングFFTで高周波数分解能にするPythonコード
今回行うゼロパディングとはデータ長を2の冪に合わせるために0配列を水増しすることです。ゼロを追加するのでフーリエ変換した時の振幅スケーリング時に辻褄を合わせる必要があります。
ゼロパディング付きCooley-Tukey法のPythonコード(コピペ動作OK)
こちらがゼロパディング付きCooley-Tukey法のFFTコードです。とは言え自作なのであくまで参考までにどうぞ。ゼロパディングによる振幅補正係数acfは先ほど紹介した記事に記載のまま使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 |
import numpy as np from matplotlib import pyplot as plt import time def fft(x): """ 高速フーリエ変換(FFT):Cooley-Tukey法 """ # 標本点数 N = x.shape[0] # Nが1なら、そのままxを返す if N == 1: return x # ビット反転順序に基づいて、偶数インデックスと奇数インデックスの部分配列を得る even = fft(x[::2]) odd = fft(x[1::2]) # DFTの結果を格納するための複素数配列 T = np.exp(-2j * np.pi * np.arange(N) / N) # 偶数部分と奇数部分のDFTを組み合わせる(バタフライ演算) F = np.concatenate([even + T[:N // 2] * odd, even + T[N // 2:] * odd]) return F def fft_with_padding(x): """ FFT ゼロパディング付き """ # 元のデータの長さを保持 original_N = x.shape[0] # ゼロパディングするための長さ(2の冪)を計算 N = 2 ** np.ceil(np.log2(original_N)).astype(int) print(N) # ゼロパディング x_padded = np.pad(x, (0, N - original_N)) # 振幅補正係数 acf = (np.sum(np.abs(x)) / original_N) / (np.sum(np.abs(x_padded)) / N) # FFT F = fft(x_padded * acf) return F, original_N def fft_post(t, F): """ FFT結果から周波数軸と振幅成分を計算する """ N = len(F) dt = t[1] - t[0] freq = np.zeros(N, dtype=float) amp = np.zeros(N, dtype=float) for k in range(N): # 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)でスケーリング係数を変える。 if k == 0: sf = N else: sf = N / 2 # 振幅 amp[k] = np.sqrt(F[k].real ** 2 + F[k].imag ** 2) / sf # 周波数軸 freq[k] = k / (N * dt) return freq, amp def sample_wave(): """ サンプル波形 """ # A:変動成分振幅、f:周波数[Hz]、dc:直流成分、N:標本点数 A = 1 f = 10 dc = 1 N = 511 # サンプル波形。t:時間軸[s]、x:時間信号 t = np.linspace(0, 5, N) x = A * np.sin(2 * np.pi * f * t) + dc return t, x def plot(t, x, freq, amp): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(7, 5)) ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('t[s]') ax1.set_ylabel('x') ax2.set_xlabel('Frequency[Hz]') ax2.set_ylabel('X') # スケールの設定をする。 #ax2.set_xlim(0.0, 20.0) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t, x, label='time', lw=1, color='red') ax2.plot(freq, amp, label='freq', lw=1, color='red') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' t, x = sample_wave() # 自作FFT t0 = time.time() F, original_N = fft_with_padding(x) t1 = time.time() print('FFT time=', t1 - t0, '[s]') # 周波数軸と振幅の計算 freq, amp = fft_post(t, F) # プロット plot(t, x, freq, amp) |
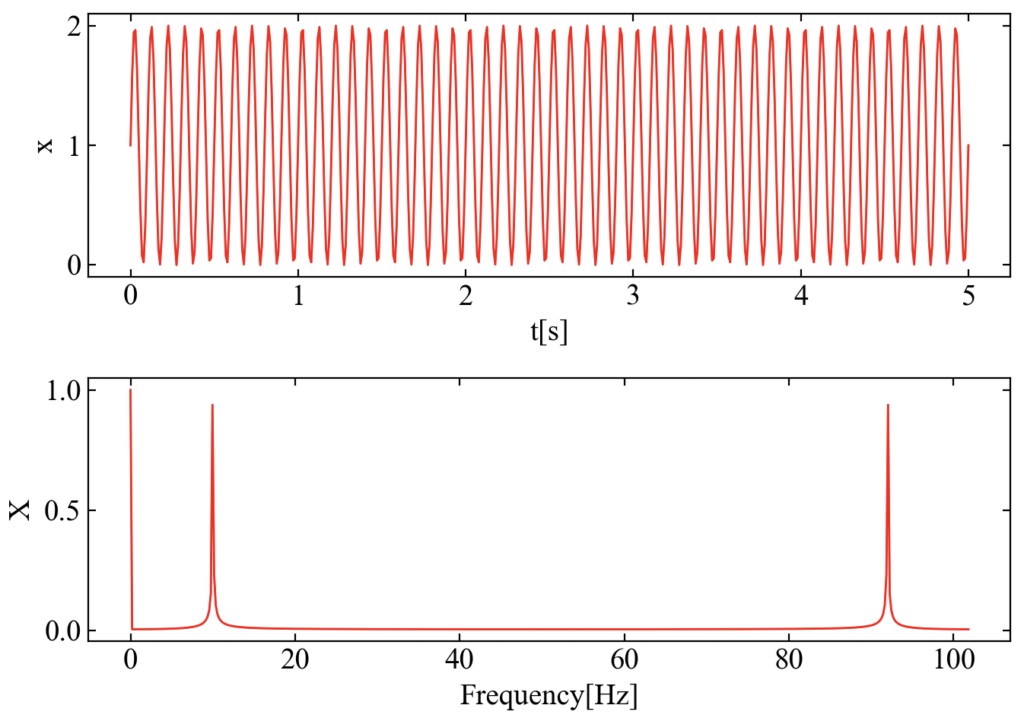
実行結果:時間波形と周波数波形
データポイント数Nを511と外していますが、エラーにならない結果を得ました。511点がゼロパディングにより512点になりました。
1800点のデータでもトライ。2048点にゼロパディングされてエラーなしで終了です。
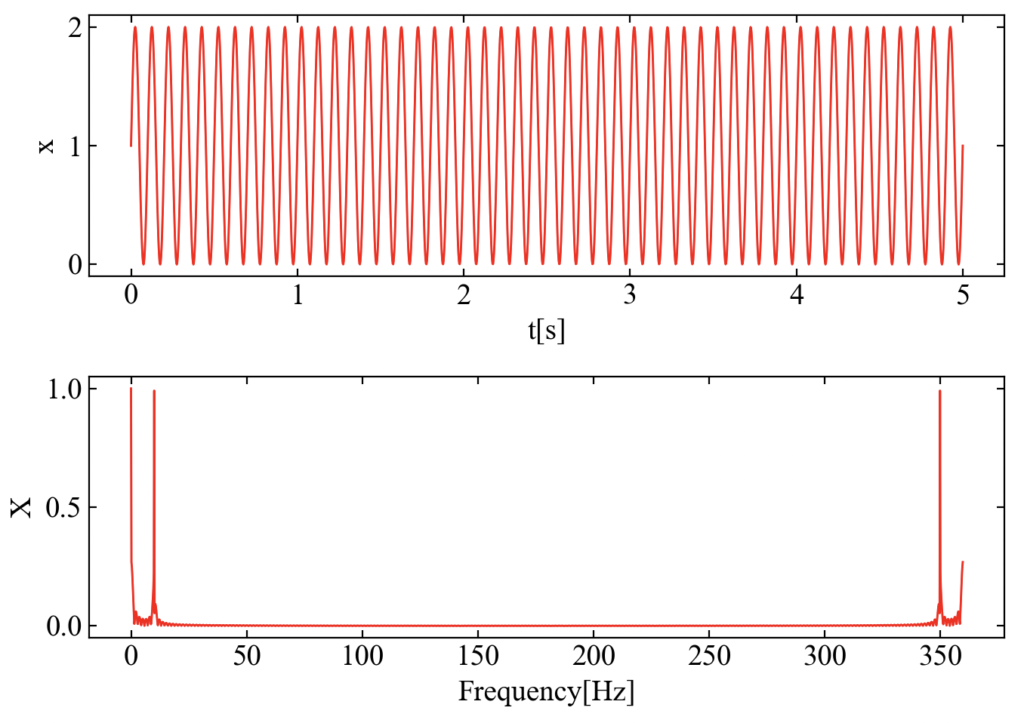
振幅補正係数を使っているのでそれなりに正しい振幅が得られている傾向はありますが、ややゼロパディングすると小さい振幅になっているような…。ここはもしかしたらバグがどこかにありそうです(まだ探せていないのでToDoにしておきます)。
データサンプル数と計算時間の関係
2の冪乗データ数をわずかに超えると、ゼロパディングにより次の冪乗数になるため容易に理解できる結果となりました。
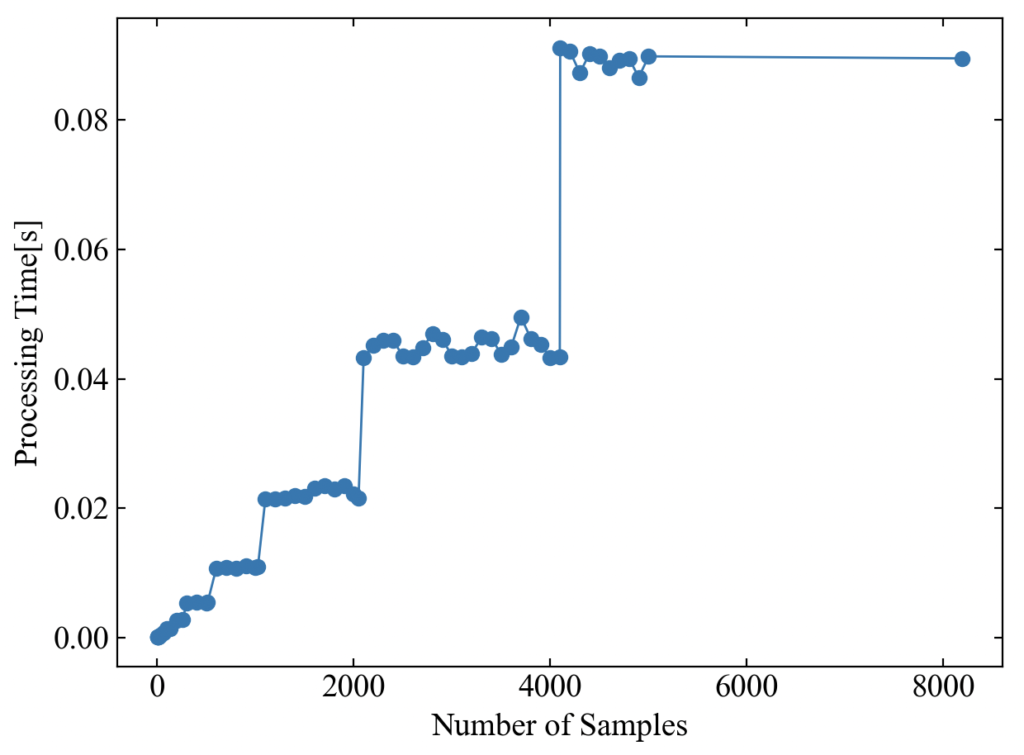
調査用コードも貼っておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 |
import numpy as np from matplotlib import pyplot as plt import time def fft(x): """ 高速フーリエ変換(FFT):Cooley-Tukey法 """ # 標本点数 N = x.shape[0] # Nが1なら、そのままxを返す if N == 1: return x # ビット反転順序に基づいて、偶数インデックスと奇数インデックスの部分配列を得る even = fft(x[::2]) odd = fft(x[1::2]) # DFTの結果を格納するための複素数配列 T = np.exp(-2j * np.pi * np.arange(N) / N) # 偶数部分と奇数部分のDFTを組み合わせる(バタフライ演算) F = np.concatenate([even + T[:N // 2] * odd, even + T[N // 2:] * odd]) return F def fft_with_padding(x): """ FFT ゼロパディング付き """ # 元のデータの長さを保持 original_N = x.shape[0] # ゼロパディングするための長さ(2の冪)を計算 N = 2 ** np.ceil(np.log2(original_N)).astype(int) print(N) # ゼロパディング x_padded = np.pad(x, (0, N - original_N)) # 振幅補正係数 acf = (np.sum(np.abs(x)) / original_N) / (np.sum(np.abs(x_padded)) / N) # FFT F = fft(x_padded * acf) return F, original_N def fft_post(t, F): """ FFT結果から周波数軸と振幅成分を計算する """ N = len(F) dt = t[1] - t[0] freq = np.zeros(N, dtype=float) amp = np.zeros(N, dtype=float) for k in range(N): # 振幅は直流成分とそれ以外(正と負の周波数成分を持つ部分)でスケーリング係数を変える。 if k == 0: sf = N else: sf = N / 2 # 振幅 amp[k] = np.sqrt(F[k].real ** 2 + F[k].imag ** 2) / sf # 周波数軸 freq[k] = k / (N * dt) return freq, amp def sample_wave(N): """ サンプル波形 """ # A:変動成分振幅、f:周波数[Hz]、dc:直流成分、N:標本点数 A = 1 f = 10 dc = 1 # サンプル波形。t:時間軸[s]、x:時間信号 t = np.linspace(0, 5, N) x = A * np.sin(2 * np.pi * f * t) + dc return t, x def plot2(N, t): ''' プロット ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Number of Samples') ax1.set_ylabel('Processing Time[s]') # データプロット ax1.plot(N, t, label='data', lw=1, marker='o') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() if __name__ == '__main__': ''' メイン処理 ''' # 2の冪乗とそれ以外のNを作成する N2 = [] for i in range(14): N2.append(2 ** i) N = [] for i in range(50): N.append((i + 1) * 100) N_append = np.sort(np.concatenate([N, N2])) # データポイント数毎に計算速度を評価するためのループ time_fft = [] for i in range(len(N_append)): t, x = sample_wave(N_append[i]) # 自作FFT t0 = time.time() F, original_N = fft_with_padding(x) t1 = time.time() print('FFT time=', t1 - t0, '[s]') time_fft.append(t1 - t0) # プロットして確認 plot2(N_append, time_fft) |
まとめ
今まで「高速フーリエ変換は難しくてライブラリを使わないで書くのは無理」と食わず嫌いしていましたが、Cooley-Tukey法であればそんなにハードなプログラミングを要求されないことがわかりました。
この記事ではDFTとFFTの違いを解説し、有名なCooley-Tukey法によるFFTコードを紹介、DFTと比べて圧倒的に計算時間が速くなることも確認しました。
また、Cooley-Tukey法ではデータサンプル数が2の冪乗でないといけませんが、ゼロパディングを使うことでその制約を排除できることを確認。これでその他の言語が信号処理ライブラリを持っていない場合でも高速フーリエ変換を実装することができそうです。
(そしてPythonではnumpyやscipyを使った方が良いというのは改めて実感しました)
参考文献
[1]:Wikipedia(E), Cooley–Tukey FFT algorithm
高速フーリエ変換(FFT)を再学習しました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!