
2Dの流体解析をする時、計算領域内部に置いた構造物の影響を考慮したくなります。ここでは画像の輪郭から流体解析に使用できる境界条件を作る1つの例を、Pythonの流体解析コードと画像処理コードをコラボしながら考察してみたいと思います。
こんにちは。wat(@watlablog)です。本日はネタ回!特に役に立たない画像処理と流体解析コードのコラボをしてみた結果をメモしました!
この記事のモチベーションと目標
2D数値計算の例
当ブログでは「Pythonで2次元ラプラス方程式を数値計算する方法」の記事で2次元(2D)空間の数値計算を行いました。
紹介した記事では学習目的であることから計算領域の中に何も条件を設定せず、4辺への境界条件を与えるというシンプルなシミュレーションを行っていました(下図)。
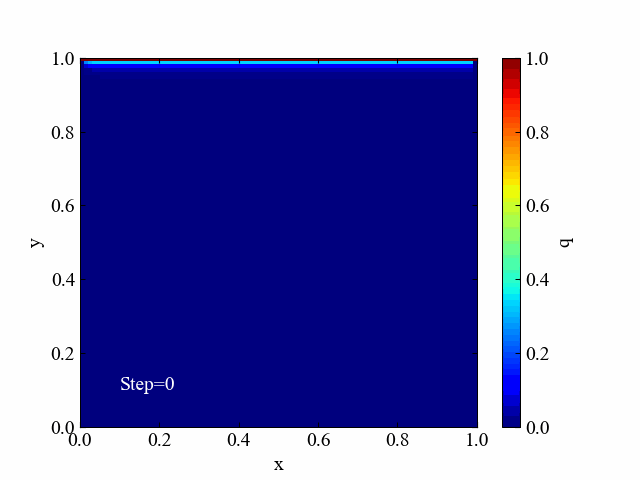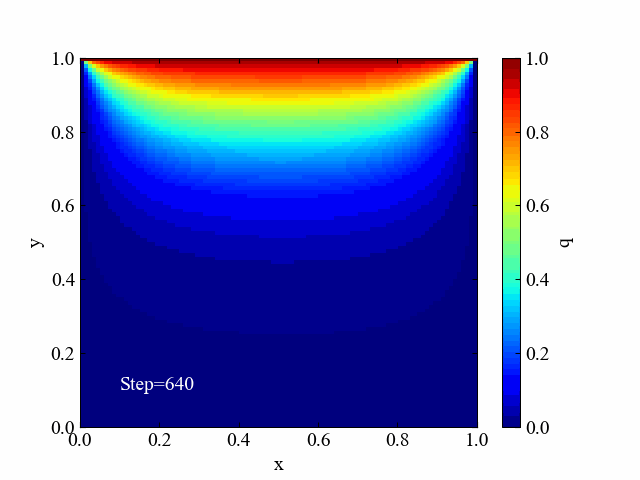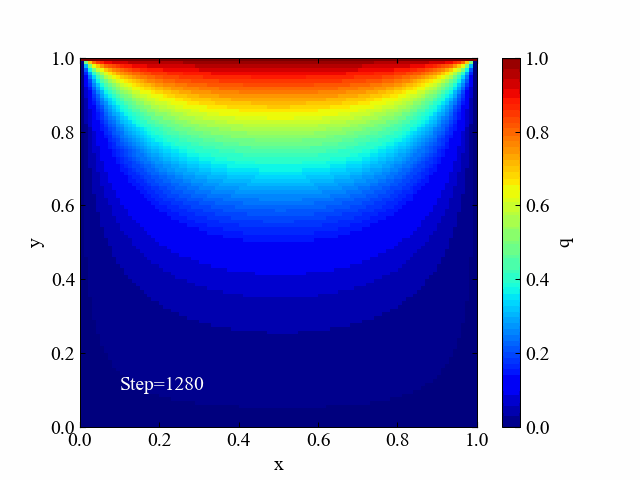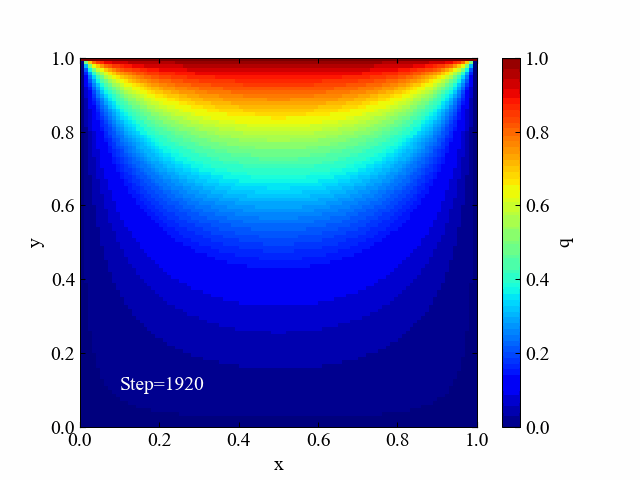
今回はこのシミュレーションをアレンジする内容として、計算領域内部に構造物を置く方法について検討してみます。
計算領域、数値計算、境界条件…といった用語が曖昧な方は是非先ほど紹介した記事をご覧になってください。
計算領域内に配置する構造物のイメージ
ここでいう構造物とは下図のように、計算領域内に空間とは異なる格子点を配置することを意味しています。
この図では星形の構造物を粗い点(赤点)で表現しているので不格好ですが、十分な解像度を持てば複雑な形状も計算領域内に表現可能です。
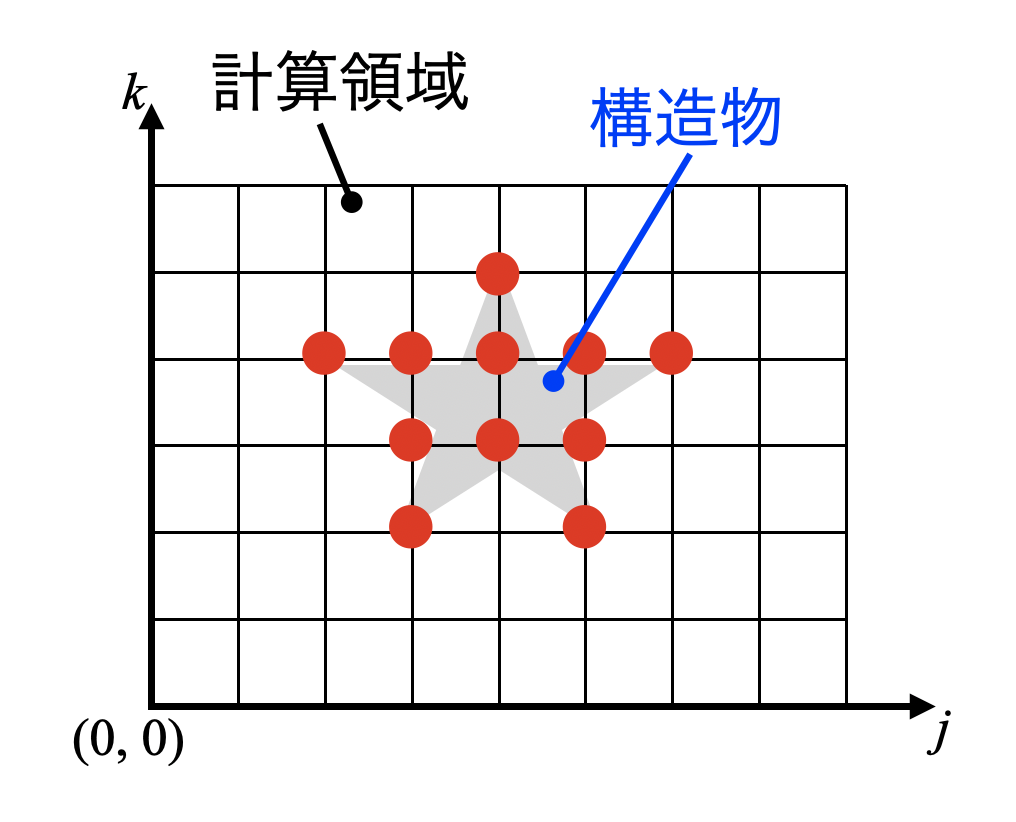
矩形や円形ならまだしも、複雑な形状を置きたい場合はプログラミング時に苦労します。例えば上記直交格子の場合は、\(j,k\)番目の反復計算時に何らかの分岐を作る必要があります。
目標:画像から境界条件を設定する格子点を自動抽出する
そこで本題です。この記事では2Dの数値計算において、画像から境界条件を設定する格子点を自動抽出することを目標とします。
下図のように、画像の複雑な輪郭を自動抽出し座標情報に変換してしまえば、数値計算時の条件分岐にそのまま使うことができます。

本ページの目標を以下の動画に示します。複雑な境界条件を画像から自動設定して2Dシミュレーションに活用するところとします。複雑な形状…という意味で漢字にしてみました。
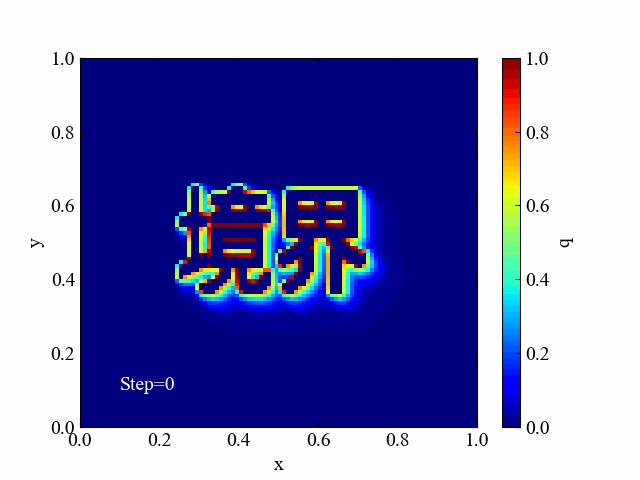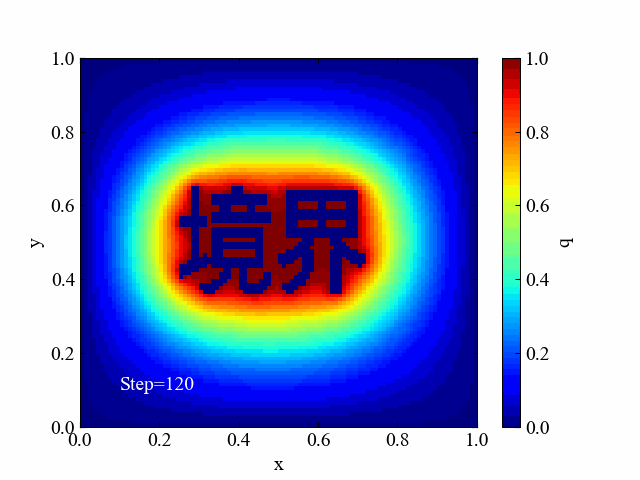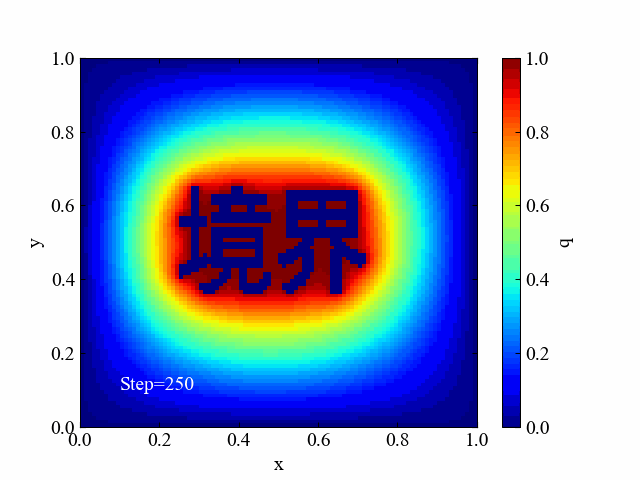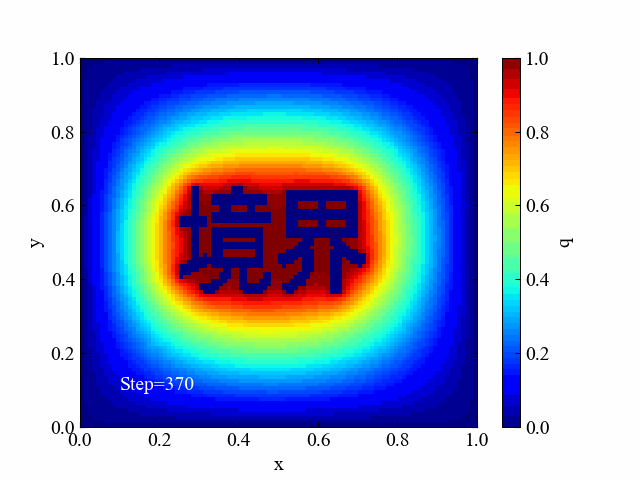
今回はノリだけで書いています。正式な数値解析のメッシュ分割法にはもっと良いやり方があると思いますが、それらを無視してできそうだったのでやってみたというだけ…。
画像内オブジェクト情報を使って2D数値計算するPythonコード
動作環境
今回は以下の環境でコーディングしました。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
| pillow | 7.1.2 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
サンプル画像
境界条件を設定する「境界」の文字が書かれた(描かれた?)画像ファイルimg-kyoukai.pngをこちらに置きます。Pythonプログラムの直下に置いて是非検証等にお使いください。ちなみにパワポで適当に文字を書いてスクショしただけです。
①画像サイズを格子に合わせる
コピペ用の全コードは最後に置きますが、まずは要所の手順説明から始めます。
先ほどの画像は適当なサイズでスクショしたものなので、計算領域との対応をとるためにまずは格子サイズの情報を使ってリサイズ(ついでにグレースケール化)を行います。
|
1 2 3 4 5 6 |
import cv2 # 画像を読み込みリサイズ後にグレースケール化 img = cv2.imread(filename, 1) img = cv2.resize(img, (w, h)) img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) |
OpenCVを用いたリサイズは以下の記事でも扱いました。
②二値化する
次に画像処理ではおなじみ、二値化処理を行います。ここでは文字部分を白く(輝度=255)したかったのでcv2.THRESH_BINARY_INVを使っています。
|
1 2 |
# 二値化 ret, img_binary = cv2.threshold(img_gray, 100, 255, cv2.THRESH_BINARY_INV) |
ちなみに、二値化にも色々種類があります。画像の状態に合わせて以下の記事も参考にしてみてください。
Python/OpenCVで画像の二値化をする方法
Python/OpenCVの適応的閾値処理で綺麗な二値化!
二値化するとこのようになります。
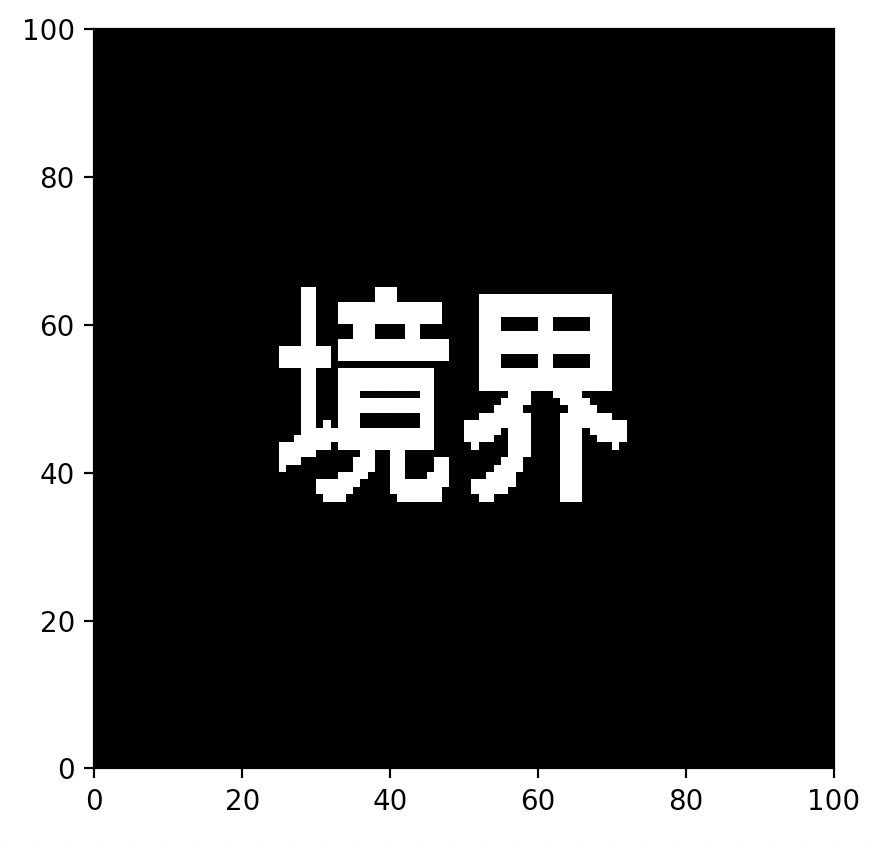
③輪郭抽出をする
輪郭抽出は以下のコードで行います。抽出した輪郭は階層構造(hierarchy)になっているので、それを一度平坦化して\(x,y\)座標のリストにしています。画像の座標と一般的なデカルト座標はy軸の方向が逆なので絶対値をかけています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
# 輪郭抽出 contours, hierarchy = cv2.findContours(img_binary, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE) img_plot(img_binary) # 位置座標化 x_boundary = [] y_boundary = [] for i in range(len(contours)): for j in range(len(contours[i])): x = contours[i][j][0][0] y = contours[i][j][0][1] x_boundary.append(x) y_boundary.append(np.abs(y)) |
こちらが抽出結果(緑線が輪郭)です。
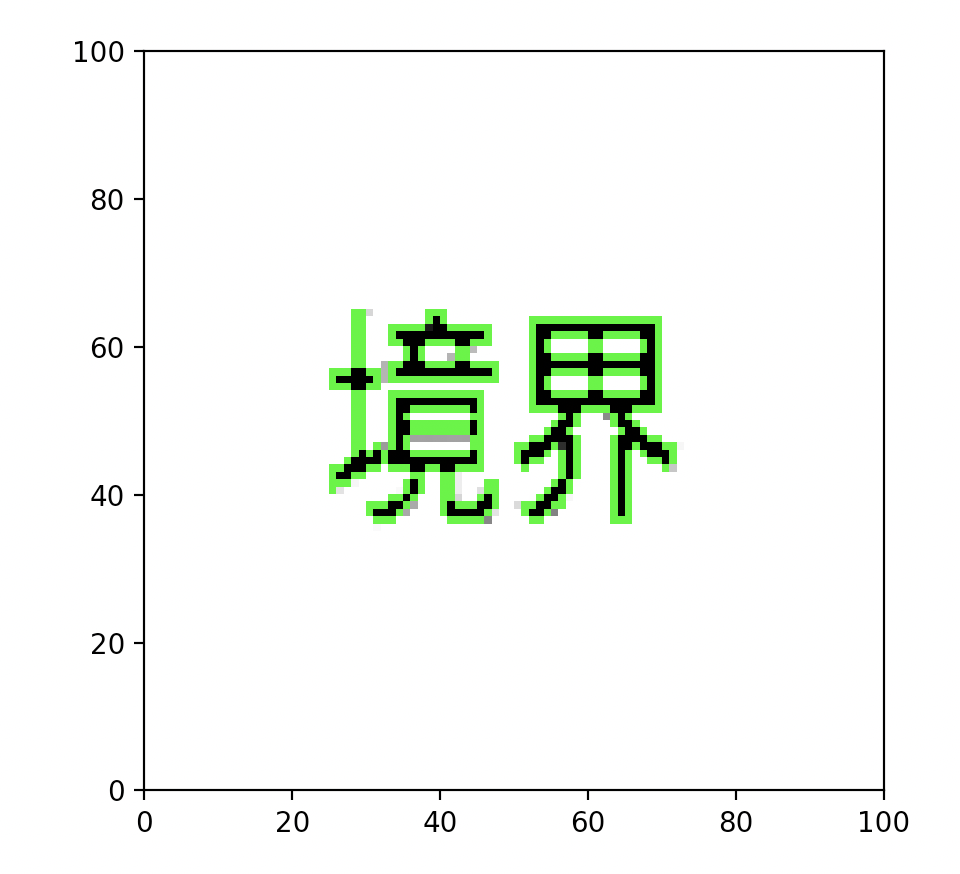
輪郭抽出は以下の記事で詳しく説明しています。
Python/OpenCVで画像内オブジェクトの輪郭抽出をする
④境界条件設定に構造の条件を追記
「Pythonで2次元ラプラス方程式を数値計算する方法」の記事で作成した境界条件を設定する関数に、今回輪郭情報を抽出した座標の条件を追記します。
ここでは辺の境界条件を0、構造の境界条件を1にしています(構造が一定温度で発熱しているイメージ)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
def boundary_condition(z, x_boundary, y_boundary): ''' 境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, :] = 0 z[-1, :] = 0 # 構造の境界条件 for i in range(len(x_boundary)): z[y_boundary[i], x_boundary[i]] = 1 return z |
全コード
以下に全コードを示します。ほとんどが既存記事のコードのままです。
しかし今回のコードはSOR法の最適な緩和係数計算が通用しません。そのため\(\omega\)は1.5を手入力しています。計算結果がおかしいと思った時は緩和係数を1にしてガウス・ザイデル法で解いてみることをお勧めします。
反復計算時、img_binaryの輝度値が255の位置における計算はしないようにしています。
計算には関係していないですが、post_img_rendering関数で計算された分布に対して元画像をレンダリングして境界をはっきりと見せています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 |
import numpy as np import cv2 from matplotlib import pyplot as plt import time from PIL import Image import os import glob def image2boundary(filename, w, h): ''' リサイズ後の画像内オブジェクトの輪郭を抽出して境界条件座標に変換する ''' # 画像を読み込みリサイズ後にグレースケール化 img = cv2.imread(filename, 1) img = cv2.resize(img, (w, h)) img_gray = cv2.cvtColor(img, cv2.COLOR_BGR2GRAY) # 二値化 ret, img_binary = cv2.threshold(img_gray, 100, 255, cv2.THRESH_BINARY_INV) # 輪郭抽出 contours, hierarchy = cv2.findContours(img_binary, cv2.RETR_LIST, cv2.CHAIN_APPROX_NONE) img_plot(img_binary) # 位置座標化 x_boundary = [] y_boundary = [] for i in range(len(contours)): for j in range(len(contours[i])): x = contours[i][j][0][0] y = contours[i][j][0][1] x_boundary.append(x) y_boundary.append(np.abs(y)) # 検証用:輪郭を画像に描画 img_contour = cv2.drawContours(img, contours, -1, (0, 255, 0), 1) img_plot(img_contour) return x_boundary, y_boundary, img_binary def img_plot(img): ''' 画像を表示させる(検証用) ''' fig = plt.figure() ax1 = fig.add_subplot(111) ax1.imshow(cv2.cvtColor(img, cv2.COLOR_BGR2RGB), extent=[0, img.shape[0], 0, img.shape[1]],) #ax1.axis('off') plt.show() plt.close() def initial_field(x_max, y_max, dx, dy): ''' 初期場を用意する ''' # 初期場 x = np.linspace(0, x_max, int(x_max / dx)) y = np.linspace(0, y_max, int(y_max / dy)) z = np.zeros((len(x), len(y))) return x, y, z def boundary_condition(z, x_boundary, y_boundary): ''' 境界条件を設定する ''' # 境界条件(左右上下) z[:, 0] = 0 z[:, -1] = 0 z[0, :] = 0 z[-1, :] = 0 # 構造の境界条件 for i in range(len(x_boundary)): z[y_boundary[i], x_boundary[i]] = 1 return z def plot(x, y, z, i): ''' 関数をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意して上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # 構造要素をレンダリング z = post_img_rendering(z, img_binary) # データをプロットする。 im = ax1.imshow(z, vmin=0, vmax=1, extent=[np.min(x), np.max(x), np.min(y), np.max(y)], aspect='auto', cmap='jet') ax1.text(0.1, 0.1, 'Step='+str(i), color="white") # カラーバーを設定する。 cbar = fig.colorbar(im) cbar.set_label('q') # 画像を保存する。 # dirフォルダが無い時に新規作成 save_dir = 'img-laplace2d' if os.path.exists(save_dir): pass else: os.mkdir(save_dir) # 画像保存パスを準備 path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png']) # 画像を保存する plt.savefig(path) # グラフを表示する。 #plt.show() plt.close() def sol_2d_laplace(dx, dy, z, x_boundary, y_boundary, img_binary, tolerance): ''' 2次元ラプラス方程式を解く ''' # 初期化 z0 = z.copy() residual = 1e20 # 緩和係数 omega = 1.5 # 反復計算=>残差がトレランスより小さくなったら終了 t0 = time.time() i = 0 print('----------Start iteration----------') while residual > tolerance: # 未知数を計算 for j in range(1, len(z) - 1): for k in range(1, len(z.T) - 1): if img_binary[j, k] == 0: z[j, k] = (1 - omega) * z[j, k] + omega * \ ((dy ** 2) * (z[j+1, k] + z[j-1, k]) + (dx ** 2) * (z[j, k+1] + z[j, k-1])) \ / (2 * (dx ** 2 + dy ** 2)) # 境界条件を設定 z = boundary_condition(z, x_boundary, y_boundary) residual = np.sum(np.sqrt((z - z0) ** 2)) / np.sum(np.sqrt(z ** 2)) if i % 10 == 0: # ポスト処理 plot(x, y, z, i) print('Iteration=', i) print('Residual=', residual) i += 1 z0 = z.copy() t1 = time.time() print('----------End iteration----------') print('Iteration=', i) print('Residual=', residual) print('Elapsed time =', float(t1 - t0)) return z def post_img_rendering(z, img): ''' 分布に画像のオブジェクトをレンダリングする ''' z = np.where(img == 255, 0, z) return z def create_gif(in_dir, out_filename): ''' imgフォルダの複数画像からGIF画像を作る ''' # ファイルソートとリスト化 path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) imgs = [] # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0) return if __name__ == '__main__': # 計算領域(範囲と分解能)を設定 x_max = 1 y_max = 1 dx = 0.01 dy = 0.01 # 画像の輪郭から境界座標を取得 x_boundary, y_boundary, img_binary = image2boundary('img-kyoukai.png', int(x_max / dx), int(y_max / dy)) # 初期場を設定 x, y, z = initial_field(x_max, y_max, dx, dy) # 境界条件を設定 z = boundary_condition(z, x_boundary, y_boundary) # ラプラス方程式を解く z = sol_2d_laplace(dx, dy, z, x_boundary, y_boundary, img_binary, 1e-4) # GIFを保存する create_gif('img-laplace2d', 'laplace-2d-draw-boundary.gif') |
上記コードを実行すると、冒頭の動画が作成されます。

以下のような離れた場所にオブジェクトが存在する場合は、それぞれから色が発生するという結果も得られます。ラプラス方程式はポテンシャル計算に使われるため、全体を滑らかにしようとする作用があります。
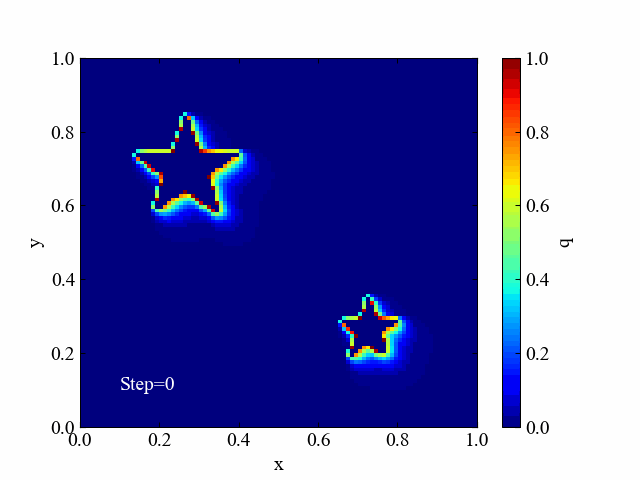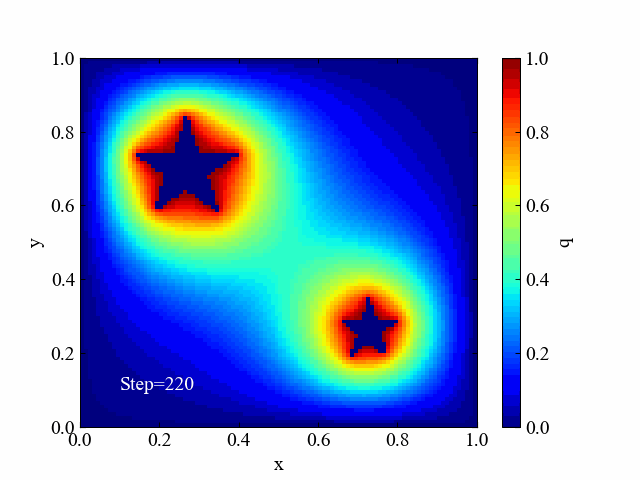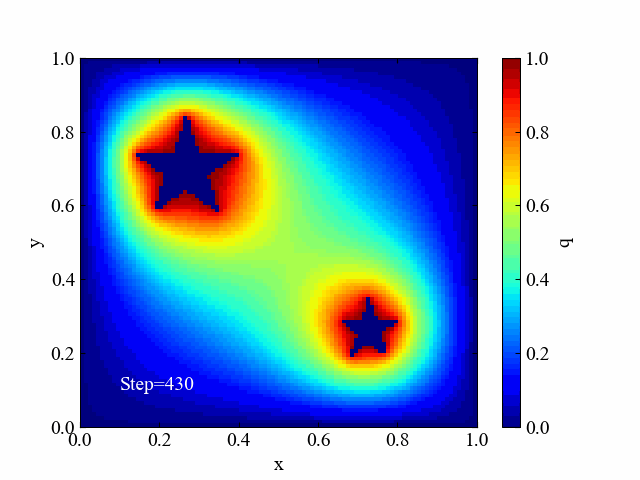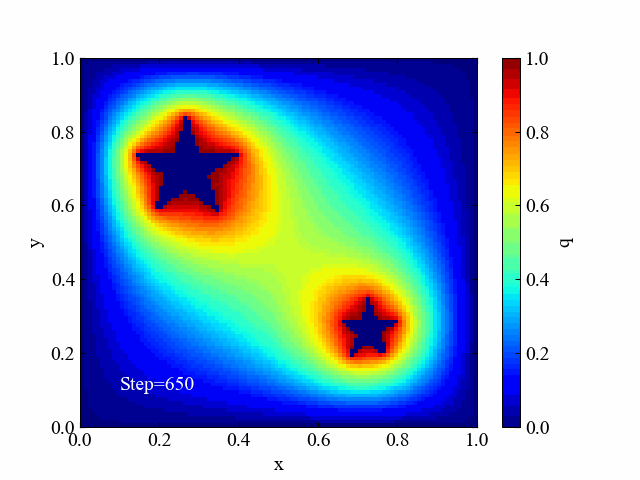
星の画像img-star.pngはこちら。コードを実行する時に「img-laplace2d」フォルダを空にしてください(動画作成に前の画像が入ってしまうため)。
まとめ
このページでは過去に学んだ2次元ラプラス方程式の数値計算コードに対して、構造物の境界を画像からつくる方法を紹介しました。
正式なメッシュ分割技法ではないと思うのであくまで参考…遊び的な内容ですが、一応思ったとおりの動作はしていると思います。
ただし、反復計算時の境界付近の取り扱いはかなり適当になっているため、計算が不安定になっているかも知れません。それらは今後の学習次第で修正を入れようと思います。
ちょっと思いついてやってみました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!