
連立方程式を反復法で解くSOR法はガウス・ザイデル法よりも高速になる可能性を持ちますが、緩和係数(加速パラメータ)の調整が必要です。ここではPythonを使ってSOR法を実装し、緩和係数のパラメータスタディと最適な緩和係数との比較を行います。
こんにちは。wat(@watlablog)です。ここではSOR法を使って連立方程式を解く方法を紹介します!
SOR法の概要
SOR法の漸化式
SOR法(Successive Over-Relaxation Method)とは、連立方程式を反復法を使って解く手法の一種です。この手法はガウス・ザイデル法に緩和係数\(\omega\)(Relaxation coefficient)を追加した漸化式を持ちます。
緩和係数\(\omega\)は加速パラメータ(Acceleration parameter)とも呼ばれますが、その名の通り反復計算の収束速度を変化させるパラメータです。
SOR法を理解するためには「Pythonで連立方程式をヤコビ法(反復法)で解く方法」と「Pythonで連立方程式をガウス・ザイデル法(反復法)で解く方法」で紹介したヤコビ法やガウス・ザイデル法の理解が必須となります。
基礎知識は上記2つの記事に記載していますので、ここではいきなり漸化式の説明から始めます。
式(1)にSOR法の漸化式を示します\(^{[1]}\)。
この式をガウス・ザイデル法の時と同様に行列形式で表すと、対角行列\(\mathbf{D}\)と剰余行列\(\mathbf{R}\)を使って式(2)と変形できます。
上添字nはステップ数です。また、剰余行列\(\mathbf{R}\)一つを使って\(x^{n+1}_{i}\)と\(x^{n}_{i}\)の係数を表現できる理由もガウス・ザイデル法の時に考察しました。
最適な緩和係数
SOR法の緩和係数\(\omega\)は自分で決める必要があり、値によってはガウス・ザイデル法よりも遅くなるため扱いが難しい手法です。
しかし、ヤコビ法の反復行列が既知であればスペクトル半径\(\rho\)から最適な緩和係数\(\omega_{opt}\)を求めることが可能です。
ヤコビ法の反復行列\(\mathbf{M}_{j}\)を式(3)に示します。
スペクトル半径\(\rho\)は正方行列の最大固有値の絶対値\(^{[2]}\)を意味しており、式(3)の行列から得られる\(\rho\)を使った最適な緩和係数\(\omega_{opt}\)は式(4)で計算されます\(^{[3][4]}\)。
ちなみに固有値はPythonを使えば簡単に求めることができます。是非「Pythonで線形代数!固有値と固有ベクトルを求める」の記事を参考にしてください。
SOR法で連立方程式を解くPythonコード
動作環境
このページでは以下の環境で動作確認を行ったコードを掲載しています。
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
PC環境
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
まずは\(\omega\)を手入力
まずはシンプルさを優先して、緩和係数\(\omega\)を手入力して解くコードを以下に示します。ヤコビ法やガウス・ザイデル法とほぼ同じなので特に詳細な説明はいらないと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 |
import numpy as np def sor(A, b, omega, tolerance): ''' 連立方程式をSOR法(反復法)で解く ''' # 検証のために乱数シードを固定 np.random.seed(314) # 係数行列を分解:D=対角成分ベクトル、R=剰余行列 D = np.diag(A) R = A - np.diag(D) # 初期化(適当な解と残差) x = np.random.random(len(b)) residual = 1e20 # 反復計算(逐次求めた解を次のループで使うため、forを使っている) iteration = 0 print('----------Start iteration----------') res = [] while residual > tolerance: # 収束判定用の1ステップ前の解を保持 x0 = x.copy() # 逐次計算 for i in range(len(x)): x[i] = (1 - omega) * x0[i] + (omega * (b[i] - R[i] @ x) / D[i]) # 収束判定 residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2)) res.append(residual) if iteration % 100 == 0: print('Iteration=', iteration) print('Residual=', residual) print('x=', x) iteration += 1 print('----------End iteration----------') print('Iteration=', iteration) print('Residual=', residual) print('x=', x, '\n') return x if __name__ == '__main__': # 係数行列と定数ベクトル A = np.array([[2, 1, 1], [2, 3, 1], [1, 1, 3]]) b = np.array([2, 4, -1]) # SOR法で解を反復計算 omega = 1.1 x_sor = sor(A, b, omega, 1e-6) print('SOR method x=', x_sor, 'Validated b=', A @ x_sor) # numpyの線形代数ライブラリで検証 x_linalg = np.linalg.solve(A, b) print('np.linalg.solve x=', x_linalg, 'Validated b=', A @ x_linalg) |
以下が結果です。
なんとたった10回の反復回数で正解を近似しました。検証として定数ベクトル\(\mathbf{b}\)の確かめ算やnp.linalg.solveの結果も実施していますが問題はありませんでした。
|
1 2 3 4 5 6 7 8 9 10 11 |
----------Start iteration---------- Iteration= 0 Residual= 0.7965770240018173 x= [ 0.53883833 0.91548019 -0.92642157] ----------End iteration---------- Iteration= 10 Residual= 8.895488523332577e-07 x= [ 0.99999964 1.00000005 -0.99999993] SOR method x= [ 0.99999964 1.00000005 -0.99999993] Validated b= [ 1.99999941 3.99999951 -1.00000009] np.linalg.solve x= [ 1. 1. -1.] Validated b= [ 2. 4. -1.] |
スペクトル半径から\(\omega_{opt}\)を求めてパラスタ結果と比較する
最適な緩和係数を求める関数
式(3)、式(4)から最適な緩和係数を求めることができるとのことなので、本当なのかどうか試してみます。また、緩和係数というパラメータを色々振ることでパラスタ(パラメータスタディ)を行い、最適値と比較します。
まずは以下に示すように、最適な緩和係数を求める関数を書いてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 |
def optimal_acc_param(A): ''' ヤコビ法のスペクトル半径から最適な緩和係数を計算する ''' # ヤコビ法の反復行列 D = np.diag(np.diag(A)) R = A - D M = - np.linalg.inv(D) @ R # スペクトル半径 eig, v = np.linalg.eig(M) rho = np.abs(np.max(eig)) # 最適な緩和係数 omega_opt = np.round(2 / (1 + np.sqrt(1 - rho ** 2)), 3) return omega_opt |
検証用の全コード
こちらが検証用の全コードです。せっかくなのでヤコビ法とガウス・ザイデル法にも登場していただき、matplotlibによるプロットで視覚的に確かめてみます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 178 179 180 181 182 183 184 185 186 187 188 189 190 191 192 193 194 195 196 197 198 199 200 201 202 203 204 205 206 207 208 209 210 211 212 213 214 215 216 217 218 219 220 |
import numpy as np from matplotlib import pyplot as plt def jacobi(A, b, tolerance): ''' 連立方程式をヤコビ法(反復法)で解く ''' # 初期化(適当な解と残差) x0 = np.random.random(len(b)) residual = 1e20 # A = D + R D = np.diag(A) R = A - np.diag(D) # 反復計算=>残差がトレランスより小さくなったら終了 i = 0 print('----------Start iteration----------') res = [] while residual > tolerance: # 解と残差を計算 x = (b - (R @ x0)) / D residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2)) res.append(residual) if i % 100 == 0: print('Iteration=', i) print('Residual=', residual) print('x=', x) i += 1 x0 = x print('----------End iteration----------') print('Iteration=', i) print('Residual=', residual) print('x=', x, '\n') return x, res def gauss_seidel(A, b, tolerance): ''' 連立方程式をガウス・ザイデル法(反復法)で解く ''' # 検証のために乱数シードを固定 np.random.seed(314) # 係数行列を分解:D=対角成分ベクトル、R=剰余行列 D = np.diag(A) R = A - np.diag(D) # 初期化(適当な解と残差) x = np.random.random(len(b)) residual = 1e20 # 反復計算(逐次求めた解を次のループで使うため、forを使っている) iteration = 0 print('----------Start iteration----------') res = [] while residual > tolerance: # 収束判定用の1ステップ前の解を保持 x0 = x.copy() # 逐次計算 for i in range(len(x)): x[i] = (b[i] - R[i] @ x) / D[i] # 収束判定 residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2)) res.append(residual) if iteration % 100 == 0: print('Iteration=', iteration) print('Residual=', residual) print('x=', x) iteration += 1 print('----------End iteration----------') print('Iteration=', iteration) print('Residual=', residual) print('x=', x, '\n') return x, res def sor(A, b, omega, tolerance): ''' 連立方程式をSOR法(反復法)で解く ''' # 検証のために乱数シードを固定 np.random.seed(314) # 係数行列を分解:D=対角成分ベクトル、R=剰余行列 D = np.diag(A) R = A - np.diag(D) # 初期化(適当な解と残差) x = np.random.random(len(b)) residual = 1e20 # 反復計算(逐次求めた解を次のループで使うため、forを使っている) iteration = 0 print('----------Start iteration----------') res = [] while residual > tolerance: # 収束判定用の1ステップ前の解を保持 x0 = x.copy() # 逐次計算 for i in range(len(x)): x[i] = (1 - omega) * x0[i] + (omega * (b[i] - R[i] @ x) / D[i]) # 収束判定 residual = np.sum(np.sqrt((x - x0) ** 2)) / np.sum(np.sqrt(x ** 2)) res.append(residual) if iteration % 100 == 0: print('Iteration=', iteration) print('Residual=', residual) print('x=', x) iteration += 1 print('----------End iteration----------') print('Iteration=', iteration) print('Residual=', residual) print('x=', x, '\n') return x, res def plot(r_jacobi, r_gauss_seidel, r_sor_i, w): ''' Residualの変化をプロットする ''' # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(8, 5)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Step') ax1.set_ylabel('Residual') # スケールの設定をする。 ax1.set_xlim(0, 60) ax1.set_yscale('log') # プロットを行う。 x1 = np.arange(0, len(r_jacobi), 1) x2 = np.arange(0, len(r_gauss_seidel), 1) ax1.plot(x1, r_jacobi, label='Jacobi', lw=4, color='red') ax1.plot(x2, r_gauss_seidel, label='Gauss-Seidel', lw=4, color='black') for i in range(len(r_sor_i)): label = str(w[i]) x = np.arange(0, len(r_sor_i[i]), 1) if i == 0: ax1.plot(x, r_sor_i[i], label='SOR $\omega$ =' + label, lw=1, color='yellow') elif i == len(w) - 1: ax1.plot(x, r_sor_i[i], label='SOR $\omega_{opt}$ =' + label, lw=1, linestyle='--') else: ax1.plot(x, r_sor_i[i], label='SOR $\omega$ =' + label, lw=1) ax1.legend(bbox_to_anchor=(1.05, 1), loc='upper left', borderaxespad=0) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() return def optimal_acc_param(A): ''' ヤコビ法のスペクトル半径から最適な緩和係数を計算する ''' # ヤコビ法の反復行列 D = np.diag(np.diag(A)) R = A - D M = - np.linalg.inv(D) @ R # スペクトル半径 eig, v = np.linalg.eig(M) rho = np.abs(np.max(eig)) # 最適な緩和係数 omega_opt = np.round(2 / (1 + np.sqrt(1 - rho ** 2)), 3) return omega_opt if __name__ == '__main__': # 係数行列と定数ベクトル A = np.array([[2, 1, 1], [2, 3, 1], [1, 1, 3]]) b = np.array([2, 4, -1]) # ヤコビ法で解を反復計算 x_jacobi, res1 = jacobi(A, b, 1e-8) print('Jacobi method x=', x_jacobi, 'Validated b=', A @ x_jacobi) # ガウス・ザイデル法で解を反復計算 x_gs, res2 = gauss_seidel(A, b, 1e-8) print('Gauss-Seidel method x=', x_gs, 'Validated b=', A @ x_gs) # SOR法で解を反復計算 omega_opt = optimal_acc_param(A) print('optimal acc. param.=', omega_opt) omega = [1.0, 1.1, 1.2, 1.3, 1.4, 1.5, 1.6, 1.7, 1.8, 1.9, 2.0] omega.append(omega_opt) res = [] for i in range(len(omega)): x_sor, res_i = sor(A, b, omega[i], 1e-8) res.append(res_i) print('SOR method x=', x_sor, 'Validated b=', A @ x_sor) # プロット plot(res1, res2, res, omega) |
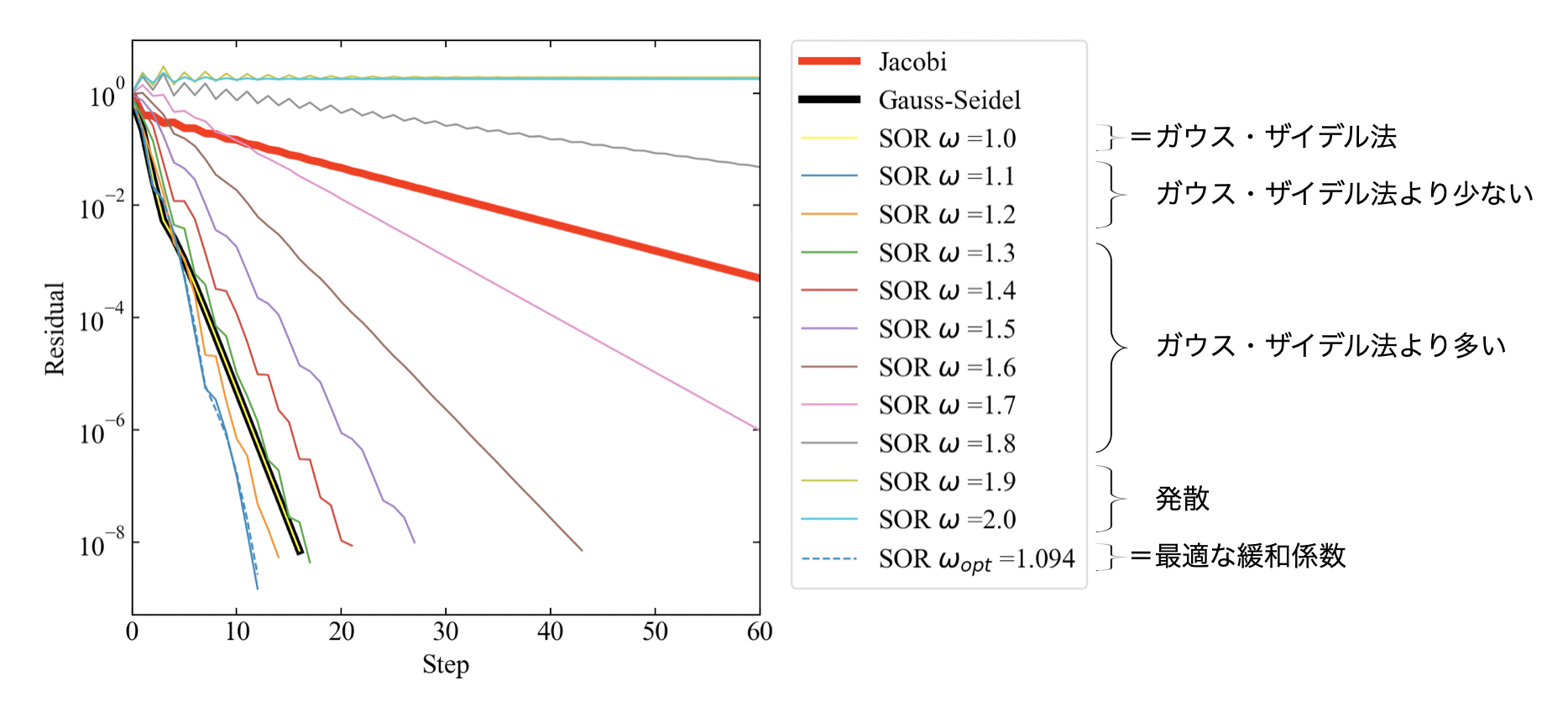
下図が結果です。緩和係数\(\omega\)が1.0の時はガウス・ザイデル法と一致します。今回\(\omega\)は1.0から2.0まで0.1刻みで振りましたが、この連立方程式の場合は\(\omega=\)1.9, 2.0で発散(解がでたらめになる)するといった特徴もありました。
また最適な緩和係数の場合とパラスタで得られた\(\omega\)の値が近く、式(4)はしっかり実装できているのではと考えられます(文献があまりなかったので合っているか不安でした)。
まとめ
この記事ではSOR法の概要として漸化式と最適な緩和係数(加速パラメータ)を説明しました。最適な緩和係数は行列のスペクトル半径を使って求めるということで、固有値計算を使うことがわかりました。
筆者にとって線形代数は計算手法を覚えるということが主な学習方法でしたが、今回のスペクトル半径や固有値の関係性、行列操作の意味に重点を置いて学習するのも有用と感じました。
最後にSOR法をPythonで実装するコードを紹介しました。緩和係数にもよりますがこれまでのヤコビ法やガウス・ザイデル法よりも反復回数が削減できることがわかりました。
しかし、ヤコビ法は並列計算ができるという強みがあるので一概にどの手法が良いかは決まらないと思います。
参考文献
[1]:幸谷智紀, 連立一次方程式の解法2 -- 反復法 (2007), pp109
[3]:Varga, R. S. (2009). Matrix iterative analysis (Vol. 27). Springer Science & Business Media.
[4]:山崎郭滋, 偏微分方程式の数値解法入門, 森北出版,(2015), pp28
ヤコビ法、ガウス・ザイデル法、SOR法の3つを使えるようになりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!