Pythonで拡散方程式を数値計算してアニメーションを作成する

熱流体分野の基礎学習として、拡散方程式の離散化と数値計算を行います。拡散方程式も移流方程式と同様に安定性の議論が必要です。ここではPythonを使って自分の手で実装しながら学習し、理解を深めるためにシミュレーション結果をアニメーションで確認するコードも紹介します。

こんにちは。wat(@watlablog)です。ここでは流体現象として重要な拡散方程式をPythonで数値計算してみます！

目次（項目クリックでジャンプできます）

前回記事のおさらい

移流方程式の離散化と数値計算

前回の「Pythonで1次元移流方程式を離散化して数値流体力学に入門する」という記事では、移流方程式という偏微分方程式の数値計算を行いました。

拡散方程式の概要

拡散とは？

拡散（Diffusion）とは、液体や気体、温度といった熱流体が散らばっていき、化学変化を伴わずに次第に全体が均一になっていく現象のことです。

もっと専門的に説明すると、拡散は保存側に従う物理量について、総量を保ちつつ分布だけが拡がる現象を指します（日本機械学会より）。

上記以外にもインクや煙の広がりといった様々な拡散現象がありますが、今回はこの拡散現象の方程式を示して数値計算することを目標とします。

基礎方程式

拡散方程式（Diffusion Equation）を式（1）に示します。今回も任意の物理量を\(q\)としており、左辺左が時間項、右が二階微分形ですが空間項です。

\(\alpha\)は拡散する速度であり移流方程式の\(c\)と同じような係数となっていますが、この\(\alpha\)は物理的に正の値しかとりません。

\[ \frac{\partial q}{\partial t} - \alpha \frac{\partial^{2} q}{\partial x^{2}}=0 \tag{1} \]

離散化

移流方程式と同じように離散化します。式（2）は式（1）の偏微分方程式を離散化した結果を示します。時間項は移流方程式と同様に前進差分、空間項は2次精度中心差分で離散化しました。

\[ q^{n+1}_{j} = q^{n}_{j}+\alpha \frac{\Delta t}{\Delta x^{2}} \left ( q^{n}_{j+1}-2q^{n}_{j}+q^{n}_{j-1} \right ) \tag{2} \]

\(q\)の上添字はステップ数を、下添字は空間の格子番号を意味することも「Pythonで1次元移流方程式を離散化して数値流体力学に入門する」と同じです。式の意味が曖昧になった方は前回の記事で詳しく説明していますので、そちらをご覧ください。

安定性の判別式

離散化された拡散方程式の安定性は式（3）で確認します。移流方程式の時と同じ考え方ですが空間が2次精度であるため、左辺が0.5以下であることが安定の条件となります。

\[ \alpha \frac{\Delta t}{\Delta x^{2}} \leq 0.5 \tag{3} \]

Pythonで1次元拡散方程式を数値計算するコード

動作環境

このページでは以下の環境で動作確認を行ったコードを掲載しています。
動画作成の都合から画像処理ライブラリ等も使っています。

Python環境

Python	Python 3.9.6
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.21.1
matplotlib	3.4.3
pillow	7.1.2

PC環境

Mac	OS	macOS Catalina 10.15.7
	CPU	1.4[GHz]
	メモリ	8[GB]

初期分布：上に凸法物線/境界条件：両端=0

全コードを次に示します。移流方程式の数値計算と同様に、関数（sol_1d_diffusion）に必要な条件を渡してシミュレーションを実行します。

コードを実行するとimg-diffusionフォルダが作成され、そこに指定したステップ数分の解析結果画像が保存され、プログラム実行ディレクトリの直下にそれらを繋いだGIF画像1d_diffusion.gifが生成されます。

まずは初期分布qが滑らかな「上に凸の放物線」の場合を見てみましょう。

import numpy as np
from matplotlib import pyplot as plt
from PIL import Image
import os
import glob

def sol_1d_diffusion(x, q, dt, dx, alpha, step):
    ''' 1次元拡散方程式を数値計算する '''
    dir = 'img-diffusion'
    for i in range(step):
        if i % 10 == 0:
            print('Iteration=', i)
        q0 = q.copy()
        for j in range(1, len(x)-1):
            # 時間項：前進差分、空間項：2次精度中心差分
            q[j] = q0[j] + alpha * (dt / dx ** 2) * (q0[j+1] - 2 * q0[j] + q0[j-1])
        q[0], q[-1] = 0, 0
        plot(x, q, i, dir)
    create_gif(dir, '1d_diffusion.gif')
    return


def plot(x, q, i, dir):
    ''' シミュレーション結果をプロットし画像を保存する '''
    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure()

    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')

    # 軸のラベルを設定する。
    ax1.set_xlabel('x')
    ax1.set_ylabel('q')

    # スケールの設定をする。
    ax1.set_xlim(0, 10)
    ax1.set_ylim(0, 1)

    # プロットを行う。
    ax1.plot(x, q, label='Result', lw=1, color='blue')

    # レイアウト設定
    fig.tight_layout()

    # 画像を保存する。
    # dirフォルダが無い時に新規作成
    save_dir = dir
    if os.path.exists(save_dir):
        pass
    else:
        os.mkdir(save_dir)

    # 画像保存パスを準備
    path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png'])

    # 画像を保存する
    plt.savefig(path)

    # グラフを表示する。
    #plt.show()
    plt.close()
    return


def create_gif(in_dir, out_filename):
    ''' imgフォルダの複数画像からGIF画像を作る '''
    path_list = sorted(glob.glob(os.path.join(*[in_dir, '*'])))  # ファイルパスをソートしてリストする
    imgs = []                                                    # 画像をappendするための空配列を定義

    # ファイルのフルパスからファイル名と拡張子を抽出
    for i in range(len(path_list)):
        img = Image.open(path_list[i])                           # 画像ファイルを1つずつ開く
        imgs.append(img)                                         # 画像をappendで配列に格納していく

    # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。
    imgs[0].save(out_filename,
                 save_all=True, append_images=imgs[1:], optimize=False, duration=20, loop=0)
    return


if __name__ == '__main__':
    ''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する '''
    # 時間項の条件
    dt = 0.5

    # 空間項の条件
    dx = 1.0
    x_min = 0
    x_max = 11
    x = np.arange(x_min, x_max, dx)     # 1次元計算格子

    # 初期分布qと拡散速度alpha
    q = - (1 / 24) * (x - 5) ** 2 + 1
    q[0], q[-1] = 0, 0
    alpha = 1

    # 判別式の確認
    nu = alpha * dt / dx ** 2
    print('Discriminant number=', nu)

    # シミュレーションの実行
    sol_1d_diffusion(x=x, q=q, dt=dt, dx=dx, alpha=alpha, step=100)

100

101

102

103

104

105

106

107

108

109

110

111

import numpy as np

from matplotlib import pyplot as plt

from PIL import Image

import os

import glob

def sol_1d_diffusion(x, q, dt, dx, alpha, step):

''' 1次元拡散方程式を数値計算する '''

dir = 'img-diffusion'

for i in range(step):

if i % 10 == 0:

print('Iteration=', i)

q0 = q.copy()

for j in range(1, len(x)-1):

# 時間項：前進差分、空間項：2次精度中心差分

q[j] = q0[j] + alpha * (dt / dx ** 2) * (q0[j+1] - 2 * q0[j] + q0[j-1])

q[0], q[-1] = 0, 0

plot(x, q, i, dir)

create_gif(dir, '1d_diffusion.gif')

return

def plot(x, q, i, dir):

''' シミュレーション結果をプロットし画像を保存する '''

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('x')

ax1.set_ylabel('q')

# スケールの設定をする。

ax1.set_xlim(0, 10)

ax1.set_ylim(0, 1)

# プロットを行う。

ax1.plot(x, q, label='Result', lw=1, color='blue')

# レイアウト設定

fig.tight_layout()

# 画像を保存する。

# dirフォルダが無い時に新規作成

save_dir = dir

if os.path.exists(save_dir):

pass

else:

os.mkdir(save_dir)

# 画像保存パスを準備

path = os.path.join(*[save_dir, str("{:05}".format(i)) + '.png'])

# 画像を保存する

plt.savefig(path)

# グラフを表示する。

#plt.show()

plt.close()

return

def create_gif(in_dir, out_filename):

''' imgフォルダの複数画像からGIF画像を作る '''

path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする

imgs = [] # 画像をappendするための空配列を定義

# ファイルのフルパスからファイル名と拡張子を抽出

for i in range(len(path_list)):

img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く

imgs.append(img) # 画像をappendで配列に格納していく

# appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。

imgs[0].save(out_filename,

save_all=True, append_images=imgs[1:], optimize=False, duration=20, loop=0)

return

if __name__ == '__main__':

''' 条件設定を行いシミュレーションを実行、流れのGIF画像を作成する '''

# 時間項の条件

dt = 0.5

# 空間項の条件

dx = 1.0

x_min = 0

x_max = 11

x = np.arange(x_min, x_max, dx) # 1次元計算格子

# 初期分布qと拡散速度alpha

q = - (1 / 24) * (x - 5) ** 2 + 1

q[0], q[-1] = 0, 0

alpha = 1

# 判別式の確認

nu = alpha * dt / dx ** 2

print('Discriminant number=', nu)

# シミュレーションの実行

sol_1d_diffusion(x=x, q=q, dt=dt, dx=dx, alpha=alpha, step=100)

ここで移流方程式の記事と異なる点としては、境界条件（Boundary Condition）がある部分です。

main部分と関数部分で「q[0], q[-1] = 0, 0」と分布配列qの最初と最後を0にしています。これは計算領域である端っこ（境界）を規定していることから境界条件と呼ばれます。

判別式が0.5の場合

上記コードをそのまま実行すると、式（3）の判別式は0.5ちょうどになります。
以下の動画のように、実行結果はスムーズに拡散している様子がわかります。
境界条件の通り、両端が0のまま変化しています。

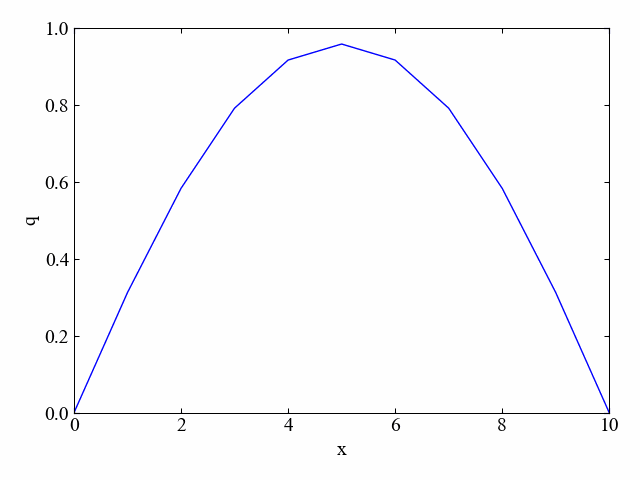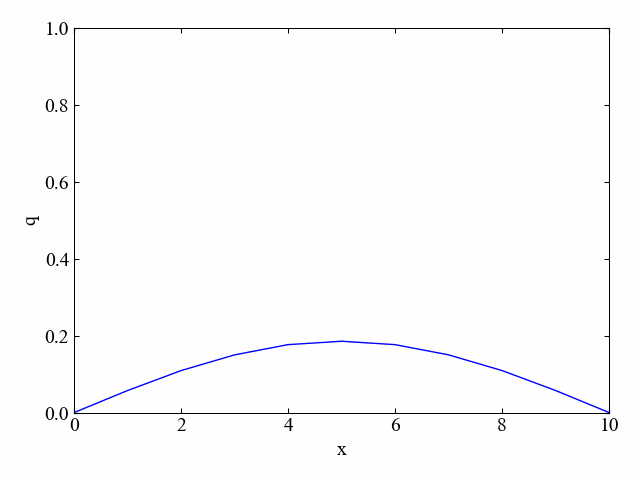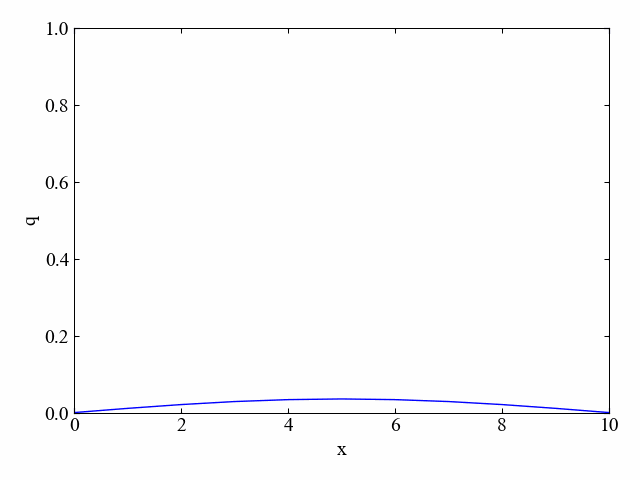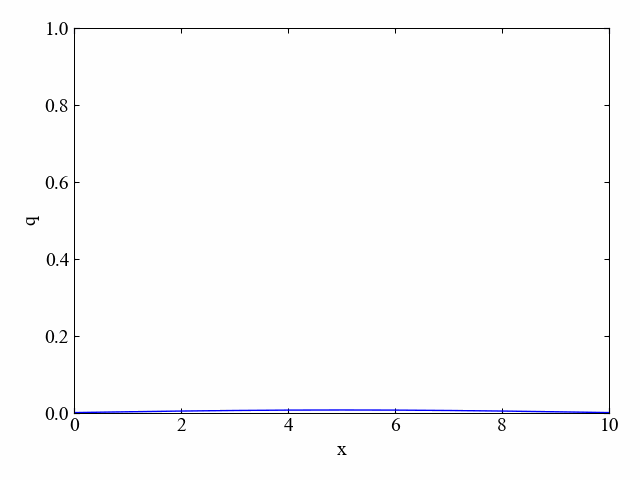
判別式が1.0の場合

「dt=1.0」と変更することで、式（3）の判別式は1.0となります。
計算結果は以下の動画です。見事に発散しました。

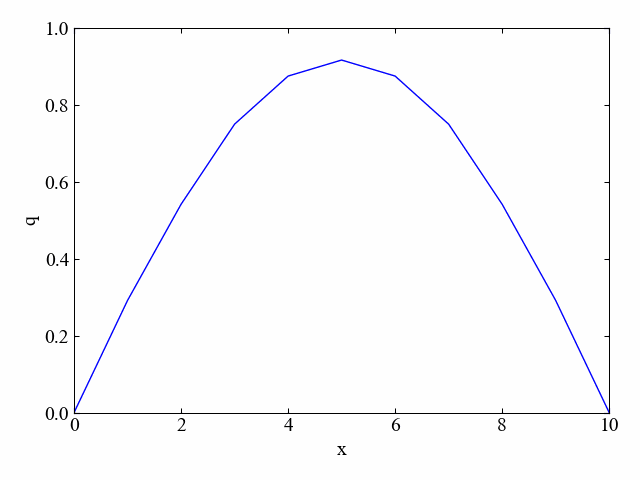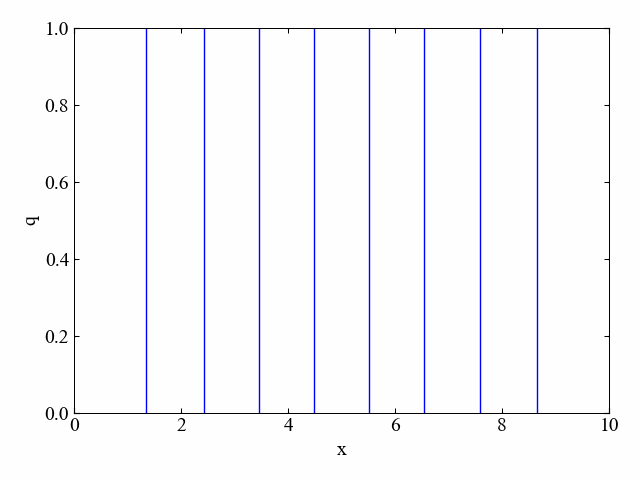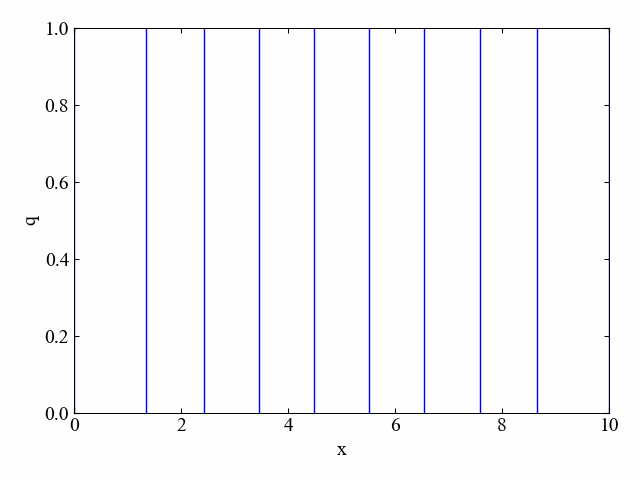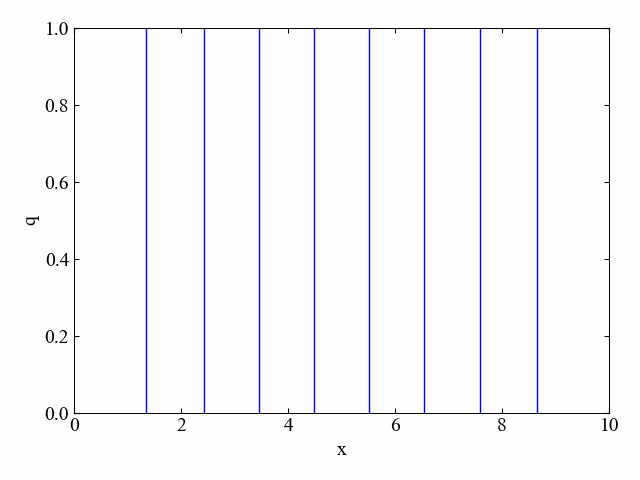
あまりにも速く爆散してしまったので、発散に到るまでの過程を静止画でも残しておきます。判別式の通り、時間と空間の分解能の大事さがよくわかりますね。

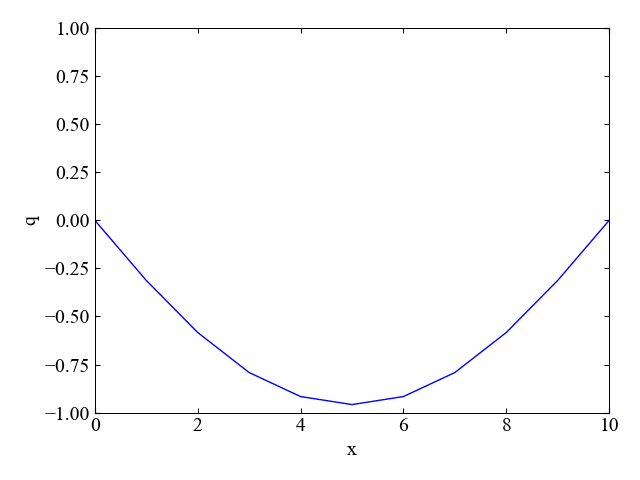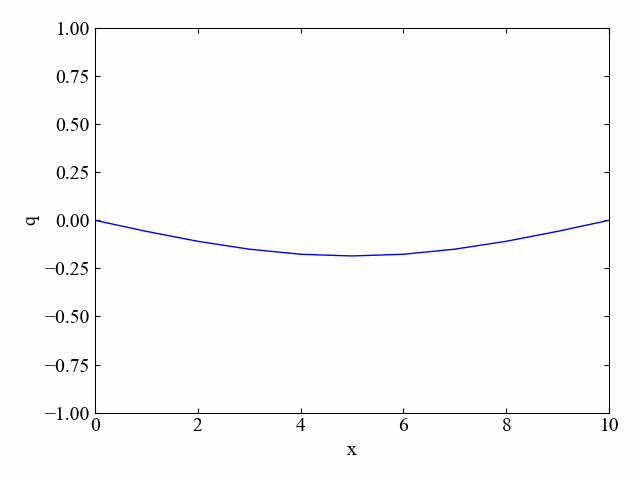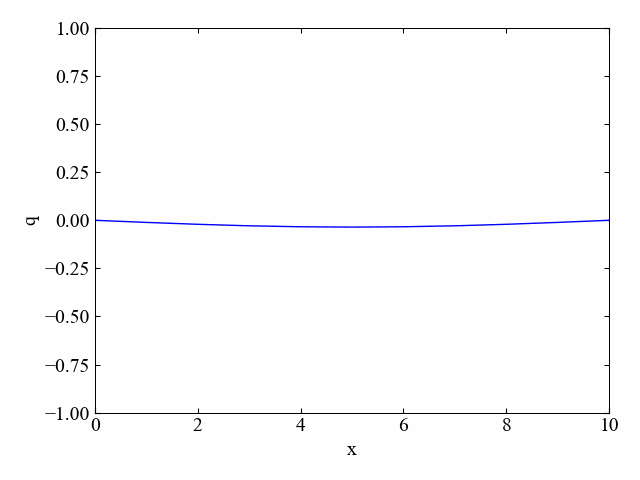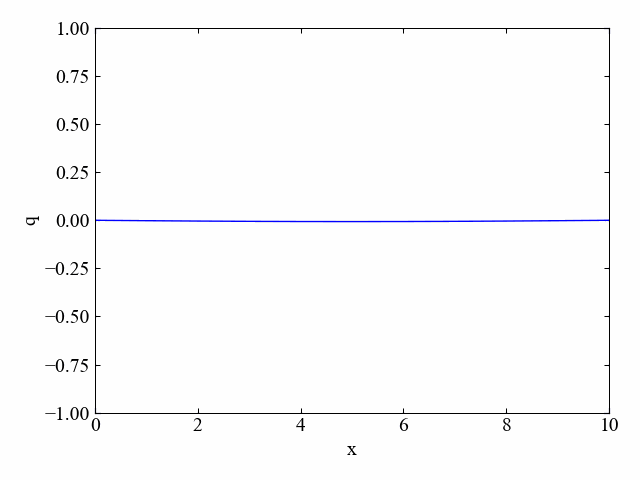
初期分布：下に凸法物線/境界条件：両端=0

次は以下のコードで初期分布を書き換え、「下に凸の放物線」で結果を見てみましょう。安定して計算できるよう、dtは0.5に戻しておきます。

# 初期分布qと拡散速度alpha
    q =  (1 / 24) * (x - 5) ** 2 - 1
    q[0], q[-1] = 0, 0
    alpha = 1

# 初期分布qと拡散速度alpha

q = (1 / 24) * (x - 5) ** 2 - 1

q[0], q[-1] = 0, 0

alpha = 1

結果はこちら。
この場合も全体的に均質になろうという拡散効果が確認されました。

まとめ

この記事では1次元拡散方程式とその離散化方法を紹介し、Pythonで数値計算するコードを紹介しました。移流方程式を扱った後だったので特に難しいことはありませんでした。

計算結果をアニメーションで確認することで、拡散方程式は時間の経過によって全体が均質になろうとする変化をしていることがわかりました。

安定性や離散化のより詳細な説明は以下の書籍が大変わかりやすいと思いますので、数値流体力学を学びたい人は是非お手に取ってみてはいかがでしょうか？

Pythonで学ぶ流体力学の数値計算法

Pythonによるシミュレーション手法やシミュレーションの考え方が正しく理解できる。本書は、学生、企業の若手技術者が、自らPythonによるシミュレーション手法やシミュレーションの考え方を一から学べる書籍です。

Amazon

楽天

拡散方程式を数値計算できました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

Pythonで拡散方程式を数値計算してアニメーションを作成する