
振動モードの定量的な相関比較にMAC(モード信頼性評価基準)という方法があります。ここではMACの概要や式を学び、Pythonで実際にMACを計算する方法を紹介します。
こんにちは。wat(@watlablog)です。ここでは覚えると大変便利なMACを計算する方法を学んでいきます!
振動分野におけるMACの概要
MACとは?
MAC(Modal Assurance Criterion)とは、日本語でモード信頼性評価基準と呼ばれる振動モード評価方法の一つです。
ここでいう振動モードとは、構造物の離散化モデルを固有値解析した結果の一つである固有ベクトルの事を意味しています。
MACは2つの固有ベクトルがどれだけ似ているかという相関に関する評価に使われます。
固有値解析、固有ベクトルについて数学的な意味は「Pythonで線形代数!固有値と固有ベクトルを求める」、特に振動モデルについて固有値解析を行う方法については「Pythonで多自由度系の固有値解析!固有振動数とモードを計算」という記事にまとめていますので、是非これらも併せてご覧下さい。
MACで固有ベクトルの相関を見る意味
解析モデルを実験と比較する
製品開発の現場で固有値解析を行った時、固有振動数と固有ベクトル(振動モード、モードシェイプとも呼ぶ)を結果として得ます。
下図は構造物を節点(Node)と線(Line)で表現したワイヤーフレームモデルです。例えば左端部Nodeを固定した場合、このモデルは各周波数\(f_{1}, f_{2}, f_{3}\dots\)で各固有ベクトル\(\phi_{1}, \phi_{2}, \phi_{3}\dots\)を持ちます。
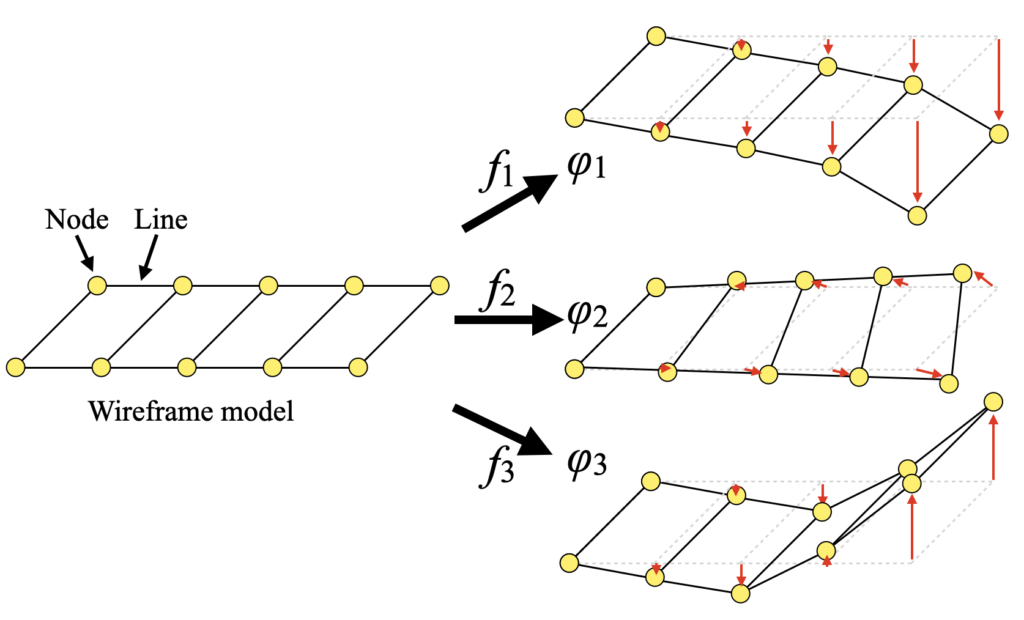
製品形状を変更して改善効果を出したい詳細設計の段階では、ある程度実際の変形状態を再現させた計算モデルを使って検討する必要がありますが、何も無い状態から実機に近い計算モデルを作るのは困難です。
そこで、振動の分野ではハンマ等による加振実験から実験モーダル解析を行い、実験的に固有ベクトルを求める事がよく行われています。
実験と解析で固有ベクトルを比較してモデルの検証を行う時にMACは使われます。
実験モーダル解析については、長松先生の下記書籍が入門者にもわかりやすく書いてありオススメできます。
固有ベクトルは簡単に定量比較できない
解析モデルを実験と比較する需要はありますが、固有ベクトルは多点の情報であるため、簡単に比較する事ができません。
固有振動数のようなスカラー値は直接数値の大小で比較ができますが、固有ベクトルはその名の通りベクトルであるため、ベクトルの相関を算出する必要があります。
例えば下のAとBの図は、人間の主観では同じ形状であると判断する事もできますが、微妙に異なる場合は「どのくらい似ているか」という数値は出ません。
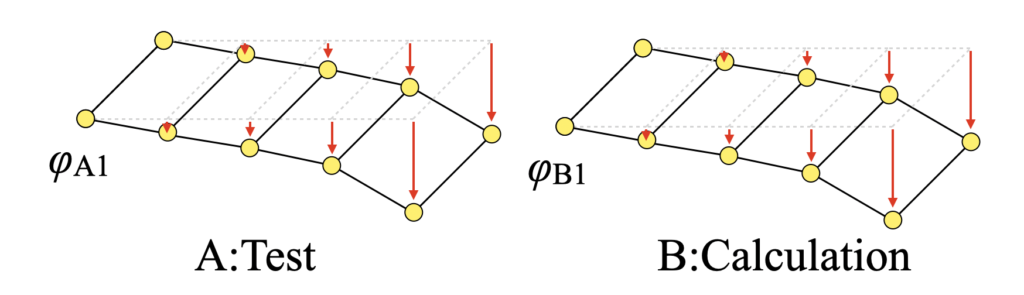
下図も同様。形が異なる事はわかりますが、「どのくらい異なるか」は図だけでは言えません。
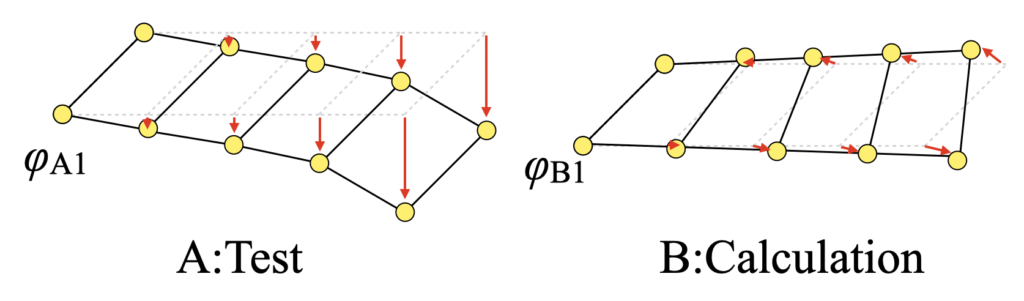
そのため、ベクトルの相関を計算する必要があります。
ベクトルや離散化関数の相関については「Pythonでベクトルと関数の相関を計算してみる」でまとめましたが、以下にコンパクトな相関を意味する式を示します。
ここで、\(\left \langle f , g \right \rangle\)は2つの関数\(f,g\)の内積を意味するのでした。そして、分母の\( \| f \| \)と\(\| g \|\)はそれぞれの関数のノルム(大きさ)です。
今回のMAC計算も、固有ベクトルの相関を定量評価するために、この式と同じ考え方をします。
MACの式
MACの計算はベクトルの相関と同じ考え方をしますが、注意点があります。
以下の図の固有ベクトルAとBの相関はどうでしょうか?
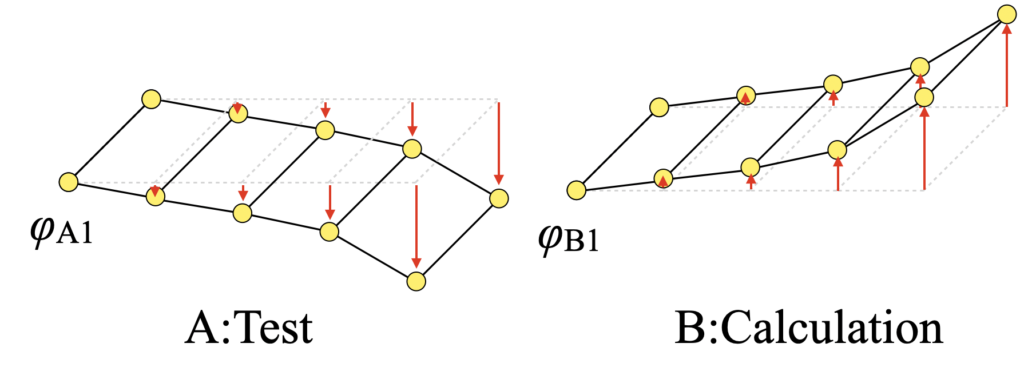
この場合、単純にベクトルの相関をとると負の相関が得られますが、振動の場合は波として考えるので両振幅として考えた時に同じであれば正の相関有りと判断します。
そのため、MACの計算式は次式になります。
分子は2つの固有ベクトルの内積により、ベクトルのなす角を求めていますが、同一方向と逆方向、つまり1と-1を同じと扱う振動モードの特徴から、絶対値をとっています。
また、分母はそれぞれ同一の固有ベクトル同士の内積を求めていますが、これはベクトルを二乗しているという意味なので、「Pythonでベクトルと関数の相関を計算してみる」で説明している内容と同じ事です。
前回記事と異なるのは、分母にルートが無い事ですが、分子を二乗しているため比としての意味も相関の考え方そのものです。
振動モードの相関の場合は、上式でMAC計算を行います。
PythonでMACを計算するコード
基本コードでMAC値検証(自己相関)
MAC値を算出するコードを紹介しますが、まずはコードの検証のために自己相関を求めてみます。ここで言う自己相関とは、モデルAとモデルBが同一の場合の相関という意味です。
今回は「Pythonでレイリー減衰を実装する方法!解析して効果を見てみる」で遊んだ以下の7自由度モデルを使います。
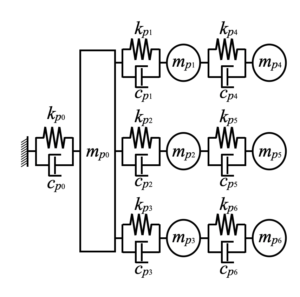
以下が全コードです。モデルを用意する関数model()と固有値解析をする関数eigen()は「Pythonで多自由度系の固有値解析!固有振動数とモードを計算」と全く同じです。
また、表を作成したりヒートマップとして色を塗ったりという部分は「Python/matplotlibで表を作成し見栄えを整える方法」で紹介している方法そのままです(この記事のために書いたものなので)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 |
import numpy as np from matplotlib import pyplot as plt # モデルA def model(): # 質量・剛性の集中定数を設定する m0 = 0.1 m1 = 0.2 m2 = 0.2 m3 = 0.4 m4 = 0.5 m5 = 0.5 m6 = 0.7 k0 = 100 k1 = 1000 k2 = 4000 k3 = 5000 k4 = 6000 k5 = 9000 k6 = 10000 M = np.array([[m0, 0, 0, 0, 0, 0, 0], [0, m1, 0, 0, 0, 0, 0], [0, 0, m2, 0, 0, 0, 0], [0, 0, 0, m3, 0, 0, 0], [0, 0, 0, 0, m4, 0, 0], [0, 0, 0, 0, 0, m5, 0], [0, 0, 0, 0, 0, 0, m6]]) K = np.array([[k0 + k1 + k2 + k3, -k1, -k2, -k3, 0, 0, 0], [-k1, k1 + k4, 0, 0, -k4, 0, 0], [-k2, 0, k2 + k5, 0, 0, -k5, 0], [-k3, 0, 0, k3 + k6, 0, 0, -k6], [0, -k4, 0, 0, k4, 0, 0], [0, -k5, 0, 0, 0, k5, 0], [0, -k6, 0, 0, 0, 0, k6]]) return M, K # 固有値解析をする関数 def eigen(M, K): # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort # MACを計算する関数 def mac(phi_a, phi_b, omega_a, omega_b): mac = np.zeros((len(phi_a), len(phi_b))) for i in range(len(phi_a)): for j in range(len(phi_b)): mac[i, j] = (np.abs(np.dot(phi_a[i].T, phi_b[j])) ** 2) / (np.dot(np.dot(phi_a[i].T, phi_a[i]), np.dot(phi_b[j].T, phi_b[j]))) # 各軸を文字列に変換して共通の文字列をさらに追加する omega_a = np.round(omega_a, 2).astype(str).astype(object) + '[Hz]' omega_b = np.round(omega_b, 2).astype(str).astype(object) + '[Hz]' # cmapを使ってデータのカラー配列を作る color_reference = 'coolwarm' cm = plt.get_cmap(color_reference) color = np.full_like(mac, 0, dtype=object) color = cm(mac) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # fig準備。 fig = plt.figure() ax1 = fig.add_subplot(111) # colorbarのためのDummyを作成 ax_dummy = fig.add_subplot(111) im = ax_dummy.imshow(mac, cmap=color_reference) ax_dummy.cla() ax_dummy.axis('off') # colorbarを設定 cbar = plt.colorbar(im) cbar.set_label('MAC($\phi_{A}, \phi_{B}$)') # 表の作成 ax1.axis('off') the_table = ax1.table(cellText=np.round(mac,2), colLabels=omega_a, rowLabels=omega_b, loc="center", cellColours=color) # 表をfigure全体に表示させる for pos, cell in the_table.get_celld().items(): cell.set_height(1 / len(mac)) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- # 質量・剛性行列を定義(今回は自己相関を見るためAとBのモデルは同一) Ma, Ka = model() Mb, Kb = model() # 固有値解析(固有振動数[Hz]と固有ベクトル[m]を計算) omega_a, phi_a = eigen(Ma, Ka) omega_b, phi_b = eigen(Mb, Kb) # MACを計算して表を作成する関数を実行 mac(phi_a, phi_b, omega_a, omega_b) |
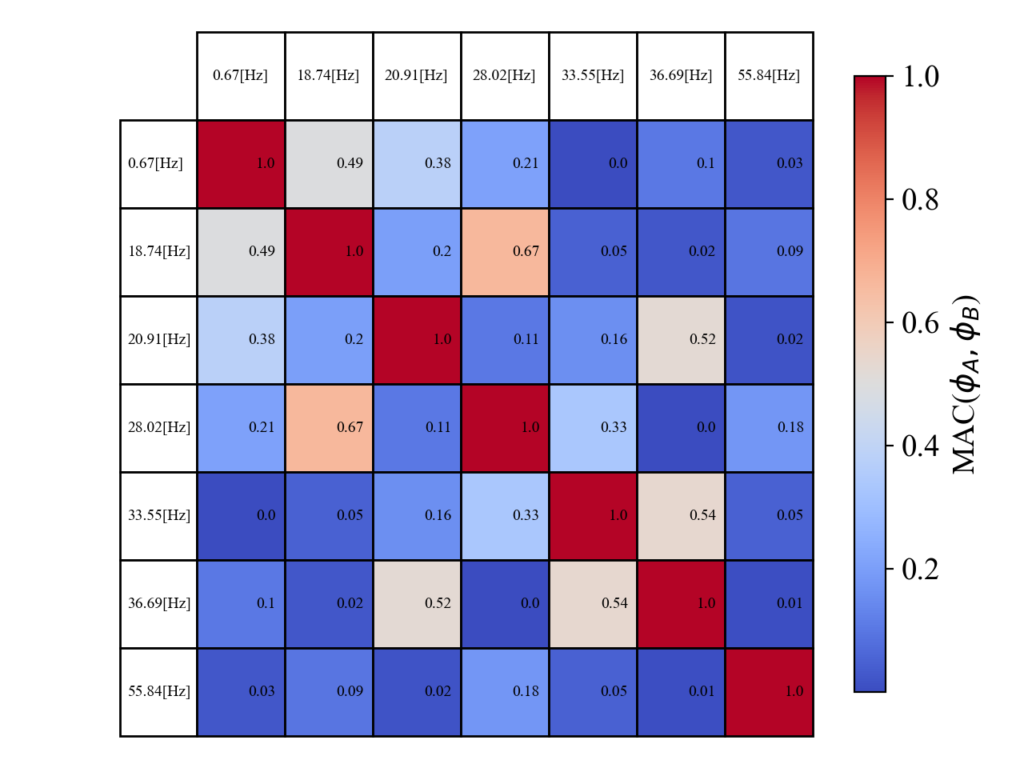
以下が結果です。同一のモデルを比較しているので、同じ固有振動数同士がクロスしている対角項は全て1.0と一致しています。これは想定通りで、まずは計算がうまくいっているようです。
異なるモデル間でMAC値を計算するコード
先ほどは同一モデルでMAC値を算出したので、対角が1となるつまらない結果でした。今度は7自由度は同一ですが、ばねマスダンパーを全て直列に繋いだモデルと比較してみます。

モデルを変更するというのは、運動方程式を変更するという意味になりますが、今回は剛性行列の中身が変わります。多自由度振動系の運動方程式の立て方は「Pythonで計算するために多自由度振動系を行列形式にする方法」で説明していますので、是非計算してみて下さい。
直列モデルの場合は剛性は決まった法則で行列が作られるのでおそらく簡単と思いますが、地道に運動方程式を立ててみる場合は「Python/SymPyで連立運動方程式の剛性行列を自動生成する」という記事で最後楽になるので、ご参考までに。
以下が異なるモデルAとBのMAC値を算出する全コードです。といっても、モデルBの関数model_b()を追加、モデル構築部分のみが変更点となります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 |
import numpy as np from matplotlib import pyplot as plt # モデルA def model_a(): # 質量・剛性の集中定数を設定する m0 = 0.1 m1 = 0.2 m2 = 0.2 m3 = 0.4 m4 = 0.5 m5 = 0.5 m6 = 0.7 k0 = 100 k1 = 1000 k2 = 4000 k3 = 5000 k4 = 6000 k5 = 9000 k6 = 10000 M = np.array([[m0, 0, 0, 0, 0, 0, 0], [0, m1, 0, 0, 0, 0, 0], [0, 0, m2, 0, 0, 0, 0], [0, 0, 0, m3, 0, 0, 0], [0, 0, 0, 0, m4, 0, 0], [0, 0, 0, 0, 0, m5, 0], [0, 0, 0, 0, 0, 0, m6]]) K = np.array([[k0 + k1 + k2 + k3, -k1, -k2, -k3, 0, 0, 0], [-k1, k1 + k4, 0, 0, -k4, 0, 0], [-k2, 0, k2 + k5, 0, 0, -k5, 0], [-k3, 0, 0, k3 + k6, 0, 0, -k6], [0, -k4, 0, 0, k4, 0, 0], [0, -k5, 0, 0, 0, k5, 0], [0, -k6, 0, 0, 0, 0, k6]]) return M, K # モデルB def model_b(): # 質量・剛性の集中定数を設定する m0 = 0.1 m1 = 0.2 m2 = 0.2 m3 = 0.4 m4 = 0.5 m5 = 0.5 m6 = 0.7 k0 = 100 k1 = 1000 k2 = 4000 k3 = 5000 k4 = 6000 k5 = 9000 k6 = 10000 M = np.array([[m0, 0, 0, 0, 0, 0, 0], [0, m1, 0, 0, 0, 0, 0], [0, 0, m2, 0, 0, 0, 0], [0, 0, 0, m3, 0, 0, 0], [0, 0, 0, 0, m4, 0, 0], [0, 0, 0, 0, 0, m5, 0], [0, 0, 0, 0, 0, 0, m6]]) K = np.array([[k0+k1, -k1, 0, 0, 0, 0, 0], [-k1, k1+k2, -k2, 0, 0, 0, 0], [0, -k2, k2+k3, -k3, 0, 0, 0], [0, 0, -k3, k3+k4, -k4, 0, 0], [0, 0, 0, -k4, k4+k5, -k5, 0], [0, 0, 0, 0, -k5, k5+k6, -k6], [0, 0, 0, 0, 0, -k6, k6]]) return M, K # 固有値解析をする関数 def eigen(M, K): # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソートして固有振動数[Hz]に変換 omega_sort = (1 / (2 * np.pi)) * np.sqrt(np.sort(omega)) # 固有値のソート時のインデックスを取得 sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) return omega_sort, v_sort # MACを計算する関数 def mac(phi_a, phi_b, omega_a, omega_b): mac = np.zeros((len(phi_a), len(phi_b))) for i in range(len(phi_a)): for j in range(len(phi_b)): mac[i, j] = (np.abs(np.dot(phi_a[i].T, phi_b[j])) ** 2) / (np.dot(np.dot(phi_a[i].T, phi_a[i]), np.dot(phi_b[j].T, phi_b[j]))) # 各軸を文字列に変換して共通の文字列をさらに追加する omega_a = np.round(omega_a, 2).astype(str).astype(object) + '[Hz]' omega_b = np.round(omega_b, 2).astype(str).astype(object) + '[Hz]' # cmapを使ってデータのカラー配列を作る color_reference = 'coolwarm' cm = plt.get_cmap(color_reference) color = np.full_like(mac, 0, dtype=object) color = cm(mac) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # fig準備。 fig = plt.figure() ax1 = fig.add_subplot(111) # colorbarのためのDummyを作成 ax_dummy = fig.add_subplot(111) im = ax_dummy.imshow(mac, cmap=color_reference) ax_dummy.cla() ax_dummy.axis('off') # colorbarを設定 cbar = plt.colorbar(im) cbar.set_label('MAC($\phi_{A}, \phi_{B}$)') # 表の作成 ax1.axis('off') the_table = ax1.table(cellText=np.round(mac,2), colLabels=omega_a, rowLabels=omega_b, loc="center", cellColours=color) # 表をfigure全体に表示させる for pos, cell in the_table.get_celld().items(): cell.set_height(1 / len(mac)) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- # 質量・剛性行列を定義 Ma, Ka = model_a() Mb, Kb = model_b() # 固有値解析(固有振動数[Hz]と固有ベクトル[m]を計算) omega_a, phi_a = eigen(Ma, Ka) omega_b, phi_b = eigen(Mb, Kb) # MACを計算して表を作成する関数を実行 mac(phi_a, phi_b, omega_a, omega_b) |
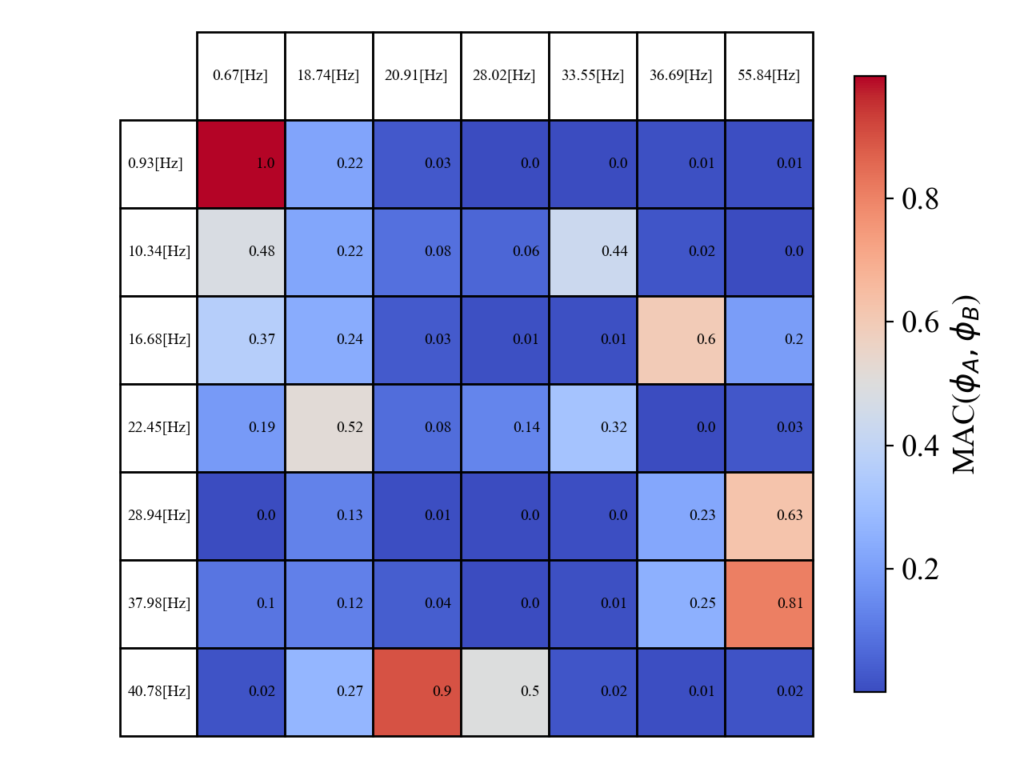
以下が結果です。横方向がモデルA(最初に紹介した7自由度振動モデル)、縦方向がモデルB(直列の7自由度振動モデル)です。使っている集中定数値は全く同じですが、モデルの形自体が異なるとMAC値も低い値ばかりとなりますね。
\(\phi_{1}\)のみMACが1なのは、モデルAも最初の要素まではモデルBと同一である事が要因と考えられます。但し、周波数は若干の違いがありました。
汎用的に使うための考察
以上でMAC計算のPythonコードを紹介しましたが、実際の業務等で使うためにはいくつか課題があると思います。このページでは作り込みまではしませんが、備忘録として思った事を書いておきます。
3次元の場合はどう考える?
本ページのモデルは7自由度ありましたが、運動の方向は全て1方向の1Dモデルでした。実際の製品設計で扱われている3Dモデルの場合はどう考えたら良いでしょうか?…というのを考えてみます。
おそらく、各節点が3次元方向に動く事が可能なモデルは下図のようになると思います。この場合、MACを計算する時に必要な固有ベクトルは単純に各方向で並べてあげれば問題ないと考えられます。
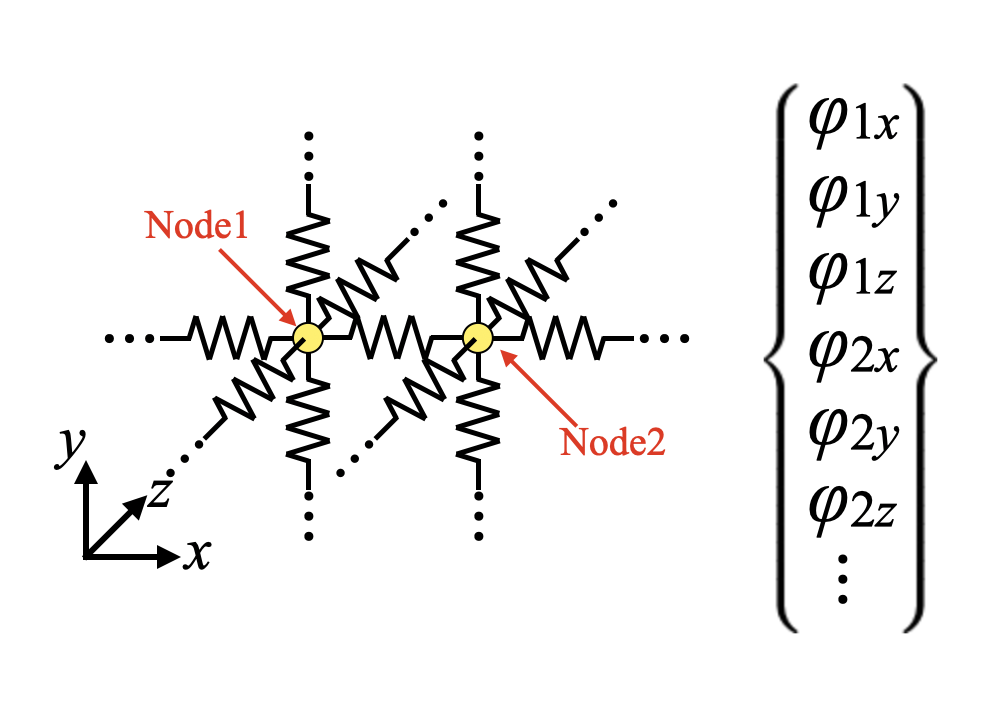
例えば、今回のPythonコードのように、シミュレーションモデルを自分で構築する時は、運動方程式を各次元、各点周りで立ててあげればよい事になります。
適切な並びがとれていれば、今回のPythonコードで問題なく計算できると思います(やってないので何とも言えませんが)。
3次元FEMの結果を使う時はどうしたら良い?
実業務の場合、解析は3次元のFEMを使うと思いますが、実験は解析で離散化した有限要素全てで測定するなんてとても出来ません。
そのため、実験の方が測定点が少なく、解析の方が多いという状況になります。
こういう時は固有ベクトルの数が大きく異なるので、解析の方で必要な点をピックアップする作業が必要と考えます。
確か有名な商用コード(DYNAとかNastranとか)は任意節点の固有ベクトルをテキスト出力できたと思いますので、専用のMAC算出ソフトが無くてもなんとかなるかも知れません(こちらもまだやってないので何とも言えませんが)。
実測した点の位置に節点を置いておく、実験の方向で解析側の固有ベクトルを並べ替える…といった作業が必要でしょうか。
やはりこれらをあまり考えなくても使える商用ソフトは優秀ですね。
まとめ
本記事では、振動モードの形、すなわち固有ベクトルを定量評価する事が可能なMACについてまとめてみました。
また、Pythonを使って実際にコーディングし、これまで習得した固有値解析を使いながら計算の検証を行いました。
実は僕は本業でMACを使っているのですが、具体的な計算方法は全く知りませんでした。知らないで使っているという事は技術者として恥ずかしいかなと思って調べたのですが、実は計算式自体は既に知っている相関の式であったという落ちです。
Pythonコードもこの式を書くだけなので苦はなかったのですが、どちらかというと表に色を付けたりカラーバーを追加したり…といった所で時間を使いました。
汎用的に使うためには色々と面倒な調整が必要かも知れませんが、まずは計算の内容を把握できた事で一区切りとします。
固有ベクトルの相関を評価するMACを覚えました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
