Pythonでベクトルと関数の相関を計算してみる

2つの物理量の間の相関を分析することは工学的問題として重要です。ここでは基本的なベクトルと関数の相関の考え方を紹介し、Pythonを使って実際に計算することで理解を深めます。

こんにちは。wat(@watlablog)です。ここではいろんな所で役立つ「相関」について整理し、Pythonで検証していきます！

目次（項目クリックでジャンプできます）

本記事の主旨

本記事ではベクトル(Vector)、関数(Function)の相関について式の導出と考え方をまとめていきます。

2つのデータが似ているとはどういうことだろう？
よく回帰曲線を引いて相関係数を出しているけど、関数の場合は一般的にどう考えるんだろう？

…と、ふと思ったことがきっかけです。

内容は初等数学的なことばかりですが、おそらく普段はExcel等で自動で計算している人が多いと思い、図を書きながらまとめていきます。

また、今回はPythonでプログラミングを行い、実際に相関係数を計算をしてみます。自分でプログラムを書いて動かしてみることで理解が深まると思いますので、是非写経してみて下さい。

ベクトルの相関

問題

関数の相関を説明する前に、まずは基本であるベクトル(Vector)の相関について考えていきます。

以下はベクトル $a$ とベクトル $b$ を、始点を揃えて $x y$ 平面上にプロットした図です。
この2つのベクトルはどれくらい似ているでしょうか？というのが最初の問題です。

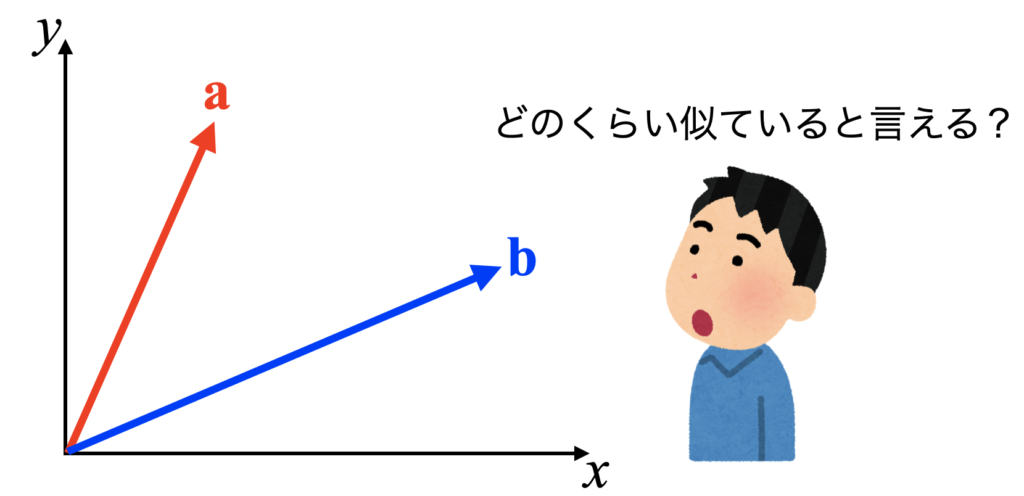
…ぱっと見で良いのであれば、「どちらのベクトルも第1象限にあり、大きさもなんとなく近い」ということでしょうが、それで良いのであればこのページを見てはいないと思います。

相関を論じる時はExcel等でお馴染みの相関係数 $r$ を用いるのが一般的です。
相関係数は、

- 1 \leq r \leq 1

…と、-1から1の範囲で値をとり、1に近いほど正の相関が、-1に近いほど負の相関が、そして0であれば無相関といった評価が可能です。

今回の問題も「相関係数がいくつ」と言えるようにしていきましょう。

$\cos θ$ で考える

まずは自明な例で見ていきます。
下図ベクトル $a$ とベクトル $b$ は大きさが等しく方向も同じであるため、正の相関があり $r = 1$ と言うことができます。

一方、ベクトル $a$ とベクトル $c$ は直交（なす角が90度）しているので、無相関( $r = 0$ )です。

さらに、ベクトル $a$ とベクトル $d$ は同じ大きさではありますが、逆方向（なす角が180度）であるため、負の相関（ $r = - 1$ ）があるとなります。

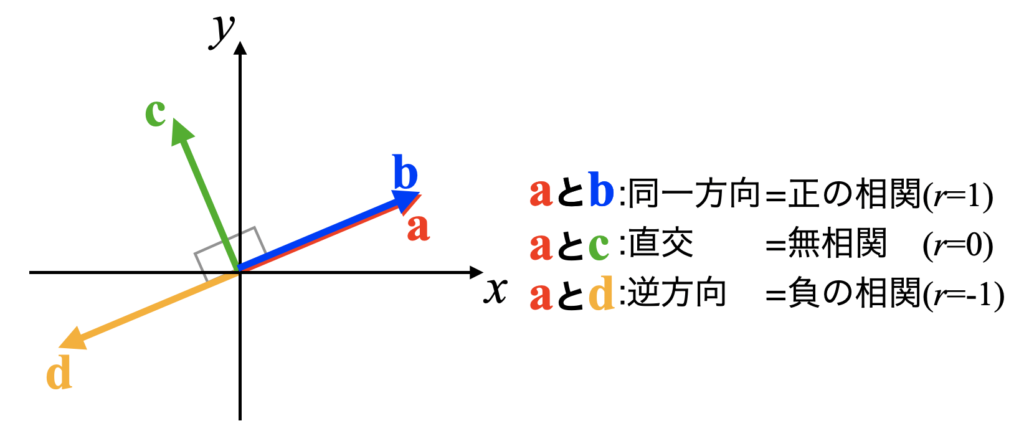
これらの関係性とぴったり一致するのが $\cos θ$ です。

$\cos θ$ は0[deg.]で1, 90[deg.]で0, 180[deg.]で-1のため、このような相関を数値化するのにとても適しています。

ベクトルの相関係数を計算する式

検討を進める糸口がつかめたので、ベクトルの相関係数を計算する式を考えてみます。そのために、先ほどの問題図に色々書き込んでみました。

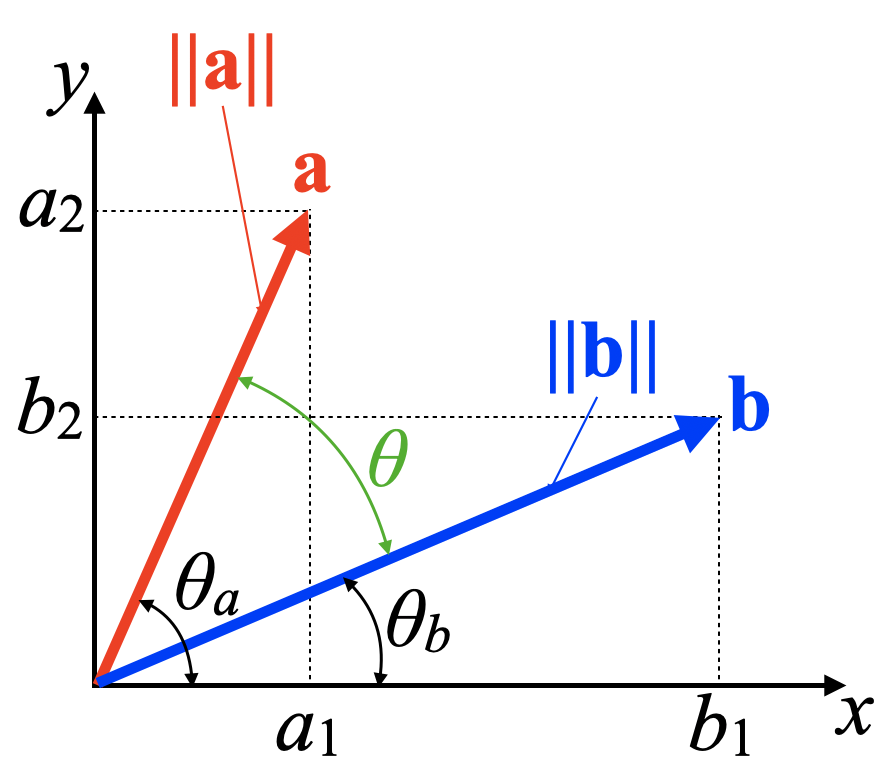
図中 $‖ a ‖$ と $‖ b ‖$ はベクトルの長さ（Norm:ノルム）で、式(1)で定義されます。

\begin{matrix} (1) & {\begin{cases} ‖ a ‖ = \sqrt{a_{1}^{2} + a_{2}^{2}} \\ ‖ b ‖ = \sqrt{b_{1}^{2} + b_{2}^{2}} \end{cases} \end{matrix}

ノルムにも色々種類がありますが、今回のノルムはベクトルの各項を二乗してルートをとっているのでL2ノルムと呼ばれるものです（機械学習でも出てきましたね）。

ノルムを三角形の斜辺と捉えれば、それぞれのベクトルに関係する三角関数は式(2)のように書けます。

\begin{matrix} (2) & {\begin{cases} \cos θ_{a} = \frac{a_{1}}{‖ a ‖} \\ \sin θ_{a} = \frac{a_{2}}{‖ a ‖} \\ \cos θ_{b} = \frac{b_{1}}{‖ b ‖} \\ \sin θ_{b} = \frac{b_{2}}{‖ b ‖} \end{cases} \end{matrix}

2つのベクトルの $\cos θ$ 、すなわち $\cos (θ_{b} - θ_{a})$ は、式(2)で求めた関係式で加法定理を使うと、式(3)と表現することが可能です。

\begin{matrix} (3) & \cos θ = \cos (θ_{b} - θ_{a}) = \cos θ_{b} \cos θ_{a} + \sin θ_{b} \sin θ_{a} \end{matrix}

式(3)に式(2)を代入すると、式(4)が導出されます。

\begin{matrix} (4) & \cos θ = \frac{a_{1} b_{1} + a_{2} b_{2}}{‖ a ‖ ‖ b ‖} \end{matrix}

$\cos θ$ はベクトルの相関係数と性質が等価であることと、分子が内積の形になっていることに気付くことができれば、式(4)を式(5)と表現することが可能です。

\begin{matrix} (5) & r = \cos θ = \frac{a^{T} b}{‖ a ‖ ‖ b ‖} \end{matrix}

この $r$ が相関係数です。
※厳密には平均値を引いた変動成分が相関係数で、それをしないのはパターン類似率と呼ぶそうです。

完全な無相関の場合は2つのベクトルが直交するので、 $a^{T} b = 0$ となるのが特徴です。

Pythonで2つのベクトルの相関を求めるコード

~~コードを書かないと当ブログのアイデンティティが無くなるので~~…せっかくなのでPythonコードを書いてみます。

式(5)の部分を関数にしただけなので簡単です。式自体はnp.linalg.normを使って簡略化しています。

import numpy as np

# ベクトルの相関を求める関数
def correlation_vector(a, b):
    a_norm = np.linalg.norm(a)              # aのL2ノルム
    b_norm = np.linalg.norm(b)              # bのL2ノルム
    r = np.dot(a.T, b) / (a_norm * b_norm)  # 相関係数
    return r

# ベクトルを作成して相関係数を計算する関数を実行
a = np.array([-1, 1])
b = np.array([1, 1])
r = correlation_vector(a, b)
print(r)

import numpy as np

# ベクトルの相関を求める関数

def correlation_vector(a, b):

a_norm = np.linalg.norm(a) # aのL2ノルム

b_norm = np.linalg.norm(b) # bのL2ノルム

r = np.dot(a.T, b) / (a_norm * b_norm) # 相関係数

return r

# ベクトルを作成して相関係数を計算する関数を実行

a = np.array([-1, 1])

b = np.array([1, 1])

r = correlation_vector(a, b)

print(r)

上記コードを実行するとコンソールに「0.0」が表示されます。直交の例ですね。

ちなみに、matplotlibの.quiver()で描画すると下図のようになります。

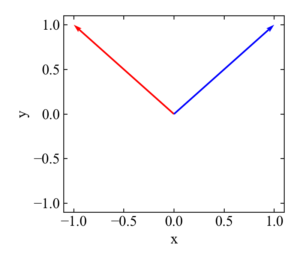
関数の相関

問題

続いて、関数(Function)の相関を考えていきます。関数といっても、先ほどのベクトルの場合と全く同じ考え方をします。

関数は本来連続的ですが、ベクトルの考え方を使うためにまずは離散関数、かつイメージしやすい時間関数を考えます。
下図は関数 $f (t)$ と $g (t)$ を $t_{0}$ から $t_{N}$ までの区間 $T$ において、刻み幅 $d t$ でサンプリングしたデータを示しています。

$f (t)$ と $g (t)$ はどれくらい似ているでしょうか？というのが問題です。

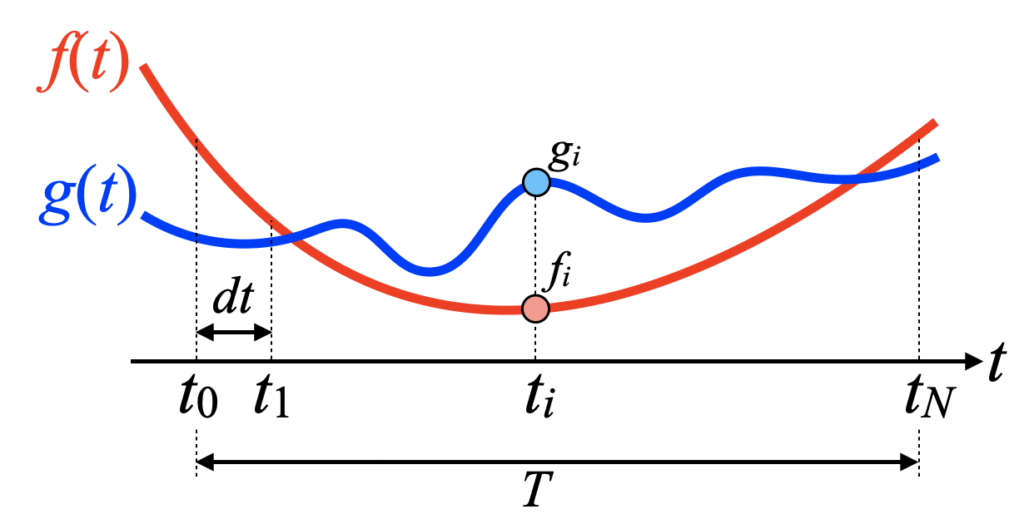
似てる？似てない？？

離散化して同一時刻 $t_{i}$ で抽出してきた $f_{i}$ と $g_{i}$ は並べてみるとベクトルです。ベクトルの相関は先ほど計算できたので、関数の場合の大きさ（ノルム）と内積を考えてみましょう。

関数の大きさを考える

冒頭の2つのベクトルに関する問題は始点を揃えていたので、ベクトルの大きさは要素の二乗和に対して平方根をとれば良いのですが、関数の場合は同じ関数でも離散数 $N$ の値で大きさが変わってしまいます。

そのため式(6)とルート内を $N$ で除することで大きさを定義します。

\begin{matrix} (6) & ‖ f ‖ = \sqrt{\frac{1}{N} \sum_{i = 0}^{N - 1} f_{i}^{2}} \end{matrix}

関数が本来連続であることを考慮すると、式(6)の $N$ を限りなく小さくすると積分記号を用いて式(7)と書くことができます。これが関数の大きさ（ノルム）を意味します。

\begin{matrix} (7) & ‖ f ‖ = \sqrt{\frac{1}{T} \int_{t_{0}}^{t_{N}} f^{2} (t) d t} \end{matrix}

内積を考える

関数の大きさを表すことができたため、次は関数の内積を考えます。
$f (t)$ と $g (t)$ の内積は、離散関数で考えると $f_{0} g_{0} + f_{1} g_{1} +, \dots, +$ と続くので、式(8)と書くことができます（ $\frac{1}{N}$ は式(6)と同様の理由で付けています）。

\begin{matrix} (8) & ⟨ f, g ⟩ = \frac{1}{N} \sum_{i = 0}^{N - 1} f_{i} g_{i} \end{matrix}

式(7)と同様に $N$ を限りなく小さくすると、積分記号を用いて式(9)と表現することが可能です。これが関数の内積を意味します。

\begin{matrix} (9) & ⟨ f, g ⟩ = \frac{1}{T} \int_{t_{0}}^{t_{N}} f (t) g (t) d t \end{matrix}

関数の相関係数を計算する式

関数の大きさと内積を式で表現することができたので、先のベクトルの場合と同様に、関数の相関係数は式(10)と書くことができます。

\begin{matrix} (10) & r = \frac{⟨ f, g ⟩}{‖ f ‖ ‖ g ‖} \end{matrix}

関数が離散である場合は、式(6)と式(8)を用いて式(11)と書くことができます（ $\frac{1}{N}$ は分母分子で打ち消し）。

\begin{matrix} (11) & r = \frac{\sum_{i = 0}^{N - 1} f_{i} g_{i}}{\sqrt{\sum_{i = 0}^{N - 1} f_{i}^{2}} \sqrt{\sum_{i = 0}^{N - 1} g_{i}^{2}}} \end{matrix}

関数が連続である場合は式(7)と式(9)を使って、式(12)と書くことができます。

\begin{matrix} (12) & r = \frac{\int_{t_{0}}^{t_{N}} f (t) g (t) d t}{\sqrt{\int_{t_{0}}^{t_{N}} f^{2} (t) d t} \sqrt{\int_{t_{0}}^{t_{N}} g^{2} (t) d t}} \end{matrix}

Pythonで2つの関数の相関を求めるコード

離散関数の場合の相関について、Pythonコードでも確認していきます。
…といっても、同一時刻でサンプリングした離散関数は先ほどのベクトルの場合と全く同じコードでいけてしまいます（ $\frac{1}{N}$ も消えるので）。

以下のコードは先に紹介したもののnp.linalg.normや転置をそのまま使い、データ作成部分のみを変更しただけになります。

関数fはサイン関数、関数gはノイズで、r_auto(fとfの自己相関)、r_cross(fとgの相互相関)の2つの相関係数を計算してみます。

import numpy as np

# 関数（離散）の相関を求める関数
def correlation_function(f, g):
    f_norm = np.linalg.norm(f)              # fのL2ノルム
    g_norm = np.linalg.norm(g)              # gのL2ノルム
    r = np.dot(f.T, g) / (f_norm * g_norm)  # 相関係数
    return r

# 関数を作成して相関係数を計算する関数を実行
t = np.arange(0, 2, 0.01)
f = np.sin(2 * np.pi * 1 * t)
g = np.random.normal(loc=0, scale=1, size=len(t))
r_auto = correlation_function(f, f)
r_cross = correlation_function(f, g)
print(r_auto, r_cross)

import numpy as np

# 関数（離散）の相関を求める関数

def correlation_function(f, g):

f_norm = np.linalg.norm(f) # fのL2ノルム

g_norm = np.linalg.norm(g) # gのL2ノルム

r = np.dot(f.T, g) / (f_norm * g_norm) # 相関係数

return r

# 関数を作成して相関係数を計算する関数を実行

t = np.arange(0, 2, 0.01)

f = np.sin(2 * np.pi * 1 * t)

g = np.random.normal(loc=0, scale=1, size=len(t))

r_auto = correlation_function(f, f)

r_cross = correlation_function(f, g)

print(r_auto, r_cross)

r_auto=1.0, r_cross≒0.0という想定通りの結果が得られました。

ちなみに、matplotlibでグラフ化すると下図になります。

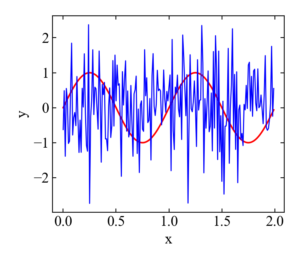
連続関数の相関は、おそらく数式をそのまま扱うsympyとか使うと普通に出来そうですが…需要は無さそう？

sympyについては「Python/sympyでテイラー展開した結果をグラフ化する方法」に概要を書いていますので、ご興味がありましたら是非読んでみて下さい。

まとめ

本記事では普段何気なく「相関」を使っている人向けに基本的なベクトルと関数の相関の考え方をまとめてみました。

多分学生の時どこかでやったかも知れないけど、いざ考え直すと忘れているものです。

工学的には理論値と実験値がどれだけ相関があるか、といった問題をよく扱います。その時に、Excelの機能にばかり頼ってしまってはカッコ悪いもの。Pythonの学習もかねて是非自分のものにしてみましょう。

※注意点
実データは様々なノイズにさらされています。相関が高いからといって安心はできないのでご注意下さい。しっかりとした分析にはきっと統計的な処理、検定等を使いこなす事が必要と思います（後でやる！）。

今回は基礎でした！申し訳程度のPythonコードでしたが、重要な事なのでマスターしましょう！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

本記事の主旨

ベクトルの相関