
信号の時間波形が振幅変調していると、フーリエスペクトルにサイドバンドが発生する事が知られています。ここでは振幅変調波の概要と、Pythonを使って様々な条件のフーリエスペクトルを計算し、サイドバンドの特性を見ていきます。
こんにちは。wat(@watlablog)です。本日はPythonプログラミングというよりも、Pythonを使って分析する回です!
ここでは振幅変調波を調べてみます!
振幅変調波の概要
変調の無い波形の式と図
振動の波形を時間波形で表現すると、最も簡単な波形は正弦波です。
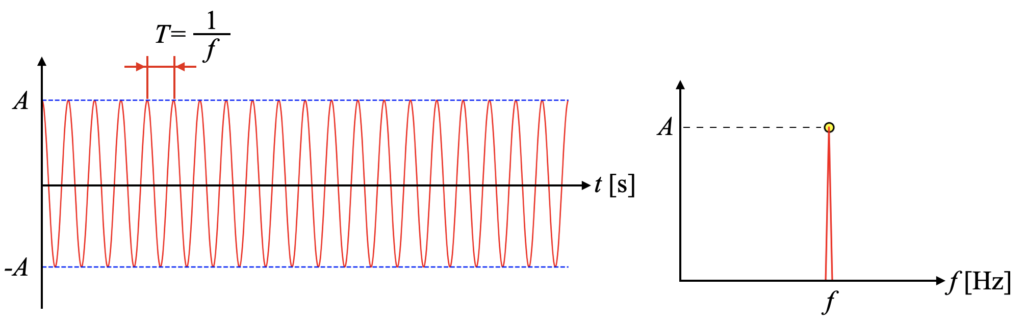
以下の式は余弦で書いていますが一緒です。振幅\(A\)、振動数\(f\)が決まれば、時間\(t\)で決まる信号\(s(t)\)が決まります。
上式の時間波形は下図左ですが、この波形をフーリエ変換して得られるフーリエスペクトルは下図右のように単一のピークが立ちます。
変調波形の式と図
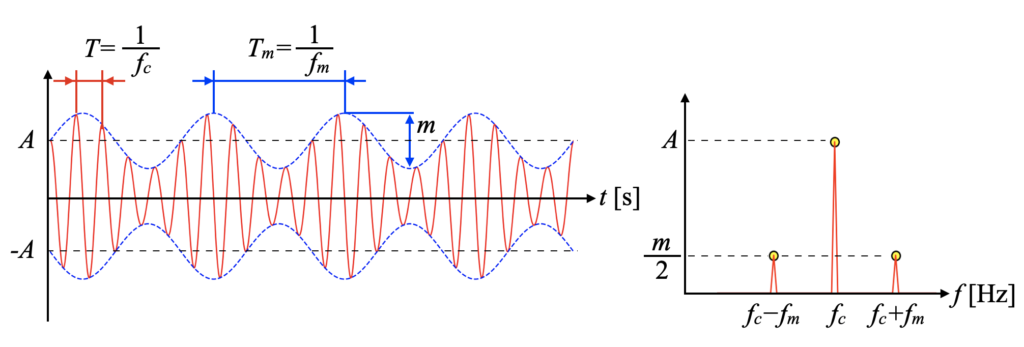
一方、振幅変調(AM:Amplitude Modulation)波とは、以下の図に示すように波の振幅成分が変動する波形の事です。
振動数\(f_{c}\)を持つ元の波形(キャリア波形)に対して振幅が別の振動数\(f_{m}\)で変動していると、この振幅変調波のフーリエスペクトルは下図右のようにピークが3つ発生します。
主のピークはもちろん\(f_{c}\)で立ちますが、その両隣にあるピーク(これをサイドバンド(側帯波)と呼ぶ)は\(f_{c} \pm f_{m}\)と\(f_{c}\)を中心として均等に離れた位置に発生する特徴を持ちます。
さらにそのサイドバンドは、変動している波の変調指数\(m\)の半分となる特徴も持ちます。
この変調指数は\(0\leq m\leq 1\)の範囲をとります。\(m=0\)の場合は変調の無い波形、\(m=1\)の場合に元の波形が0になるまで変動する事になります(下図)。
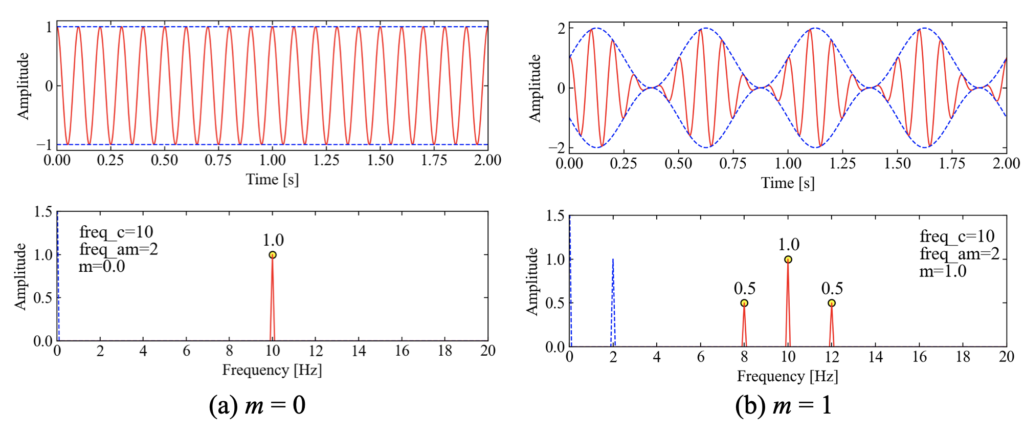
図を先行して説明しましたが、振幅変調波の式が以下になります。振幅が変動するのでキャリア波の手前にかかる振幅成分にさらに\(\cos\)がかかっています。
Pythonで振幅変調波を分析するコード
全体コード
今回の振幅変調の波形を分析するPythonコードを以下に示します。といっても、当ブログ的には新しい事は特に無く、過去記事のコードを寄せ集めただけです。
振幅変調の特徴を良く捉えるために、時間波形の包絡線(エンベロープ)をヒルベルト変換を使って求めていたり、フーリエスペクトルを得るためにSciPyのfftpackを使っていたり、ピークをmatplotlibのグラフに自動プロットするためにピーク自動検出をしていたりするコードを流用しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 |
import numpy as np from scipy import signal from scipy import fftpack import matplotlib.pyplot as plt # フーリエ変換をする関数 def calc_fft(data, samplerate): spectrum = fftpack.fft(data) # 信号のフーリエ変換 amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2)) # 振幅成分 amp = amp / (len(data) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(spectrum.imag, spectrum.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 freq = np.linspace(0, samplerate, len(data)) # 周波数軸を作成 return spectrum, amp, phase, freq # 波形(x, y)からn個のピークを幅wで検出する関数(xは0から始まる仕様) def findpeaks(x, y, n, w, extract): index_all = list(signal.argrelmax(y, order=w)) # scipyのピーク検出 index = [] # ピーク指標の空リスト peaks = [] # ピーク値の空リスト # n個分のピーク情報(指標、値)を格納 for i in range(n): index.append(index_all[0][i]) peaks.append(y[index_all[0][i]]) index = np.array(index) * x[1] # xの分解能x[1]をかけて指標を物理軸に変換 # 大きい順に任意数抽出する peaks_sort = np.sort(peaks)[::-1] index_sort = np.argsort(peaks)[::-1] index = index[index_sort] peaks = peaks_sort[:extract] index = index[:extract] return index, peaks # ヒルベルト変換で包絡線を計算する関数 def hilbert(spectrum): # 負周波数域(ナイキスト周波数以降)を0にする(実部と虚部の両方) zeros = np.zeros(int(len(spectrum) / 2)) spectrum[int(len(spectrum) / 2):len(spectrum)] = zeros # 正周波数域(ナイキスト周波数まで)を2倍する spectrum *= 2 # 操作した実部と虚部を持つ周波数波形をIFFTし、絶対値をとる(包絡線を得る) ifft_time = np.abs(fftpack.ifft(spectrum)) return ifft_time # サンプル波形を生成する。 samplerate = 25600 # サンプリング周波数 t = np.arange(0, 10, 1/samplerate) # 時間軸 amp_c = 1 # キャリア振幅 freq_c = 10 # キャリア周波数 freq_am = 2 # 変調周波数 m = 0.5 # 振幅変調指数(0<=m<=1) s = np.sin(2 * np.pi * freq_am * t) # 変調波(<=1) wave = amp_c * (1 + m * s) * np.cos(2 * np.pi * freq_c * t) # 振幅変調波 # 振幅変調波のフーリエ変換してピーク検出 spectrum, amp, phase, freq = calc_fft(wave, samplerate) index, peaks = findpeaks(freq, amp, n=100, w=6, extract=3) # ヒルベルト変換でエンベロープを作成 envelope = hilbert(spectrum) spectrum2, amp2, phase2, freq2 = calc_fft(envelope, samplerate) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Amplitude') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Amplitude') # スケールの設定をする。 ax1.set_xlim(0, 2) ax2.set_xticks(np.arange(0, 100, 2)) ax2.set_xlim(0, 20) ax2.set_ylim(0, 1.5) # データプロット ax1.plot(t, wave, label='wave', lw=1, color='red') ax1.plot(t, envelope, label='envelope', lw=1, color='blue', linestyle='dashed') ax1.plot(t, envelope * -1, label='envelope', lw=1, color='blue', linestyle='dashed') ax2.plot(freq, amp, label='wave', lw=1, color='red') ax2.plot(freq, amp2, label='wave', lw=1, color='blue', linestyle='dashed') ax2.scatter(index, peaks, color='yellow', linewidth=1, edgecolor='black') for i in range(len(index)): plt.text(index[i] - 0.5, peaks[i] + 0.1, str(round(peaks[i], 2)), fontsize=16) plt.text(16, 1.2, 'freq_c=' + str(round(freq_c, 2)), fontsize=16) plt.text(16, 1.0, 'freq_am=' + str(round(freq_am, 2)), fontsize=16) plt.text(16, 0.8, 'm=' + str(round(m, 2)), fontsize=16) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
参考の記事は以下にリンクしておきますので、是非ご覧下さい。
「PythonでFFT実装!SciPyのフーリエ変換まとめ」
「Pythonでヒルベルト変換!時間波形の包絡線を求める方法」
「PythonでFFT波形から任意個数のピークを自動検出する方法」
変調指数\(m\)を変えてみる
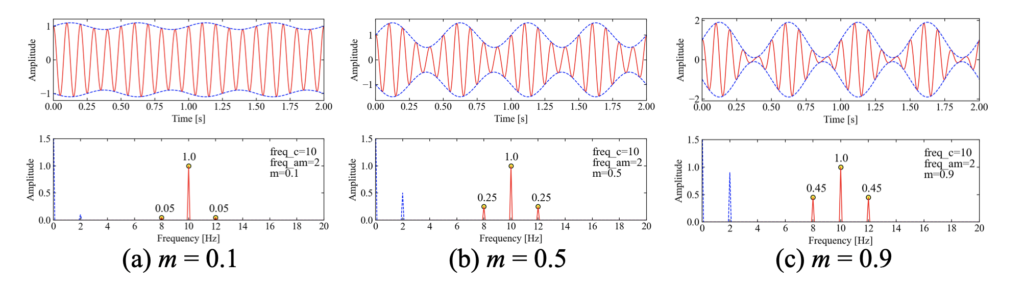
先ほどのコードを使って、パラメータスタディをしてみます。まずは変調指数\(m\)を0.1, 0.5, 0.9と変化させていきます。
以下がその結果です。\(m\)の値によって時間波形の変動の大きさが変わっている事がわかります。また、フーリエスペクトルは、主である\(f_{c}\)周波数の振幅成分は変わっていないのにも関わらず、サイドバンドの振幅が上で説明した法則である\(\frac{m}{2}\)に従っている事も確認できました。
変調周波数\(f_{m}\)を変えてみる
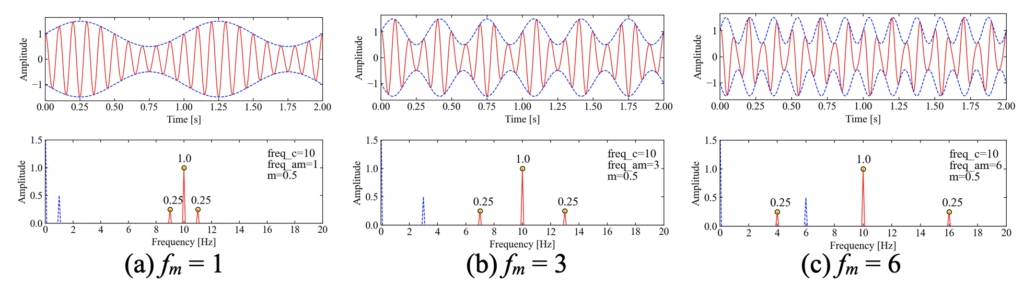
次に、変調周波数\(f_{m}\)を変えてみます。以下の結果を見ると、時間波形の振幅成分の変動具合が変化している事がわかります。
フーリエスペクトルは各ピークの振幅は変化しないにも関わらず、サイドバンドの主ピークからの離れ具合が変わっている事が確認できました。
その関係は\(f_{c} \pm f_{m}\)に従っています。
面白いですね。
まとめ
本記事ではショートTipsとして、これまで学んだPythonの信号処理技術を使って、振幅変調波の振る舞いを調べてみました。
その結果、変調指数や変調周波数によるフーリエスペクトルの変化は式で説明可能である事が確認できました。
Pythonは特にプログラミングの知識があまりなくても、高度な科学技術計算ができるようになる特徴があります。そのため、教科書に載っている式でもPythonで演算をする事で理解を深めるという事も可能です。
是非みなさんも色々な分析にPythonを使ってみて下さい。
今回は分析を中心にPythonを使ってみました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント