
Pythonは人気のある言語ですが処理速度は速くありません。しかし、NumbaのJITコンパイルを使う事で簡単に高速化が可能です。ここではNumbaのインストールからベンチマークテストを行い、最大40倍の高速化に成功した事例を紹介します。
こんにちは。wat(@watlablog)です。ここでは、処理速度がネックのPythonをNumbaというライブラリで高速化する方法を紹介します!
Pythonが遅い理由
Pythonを高速化する前に、なぜPythonはこんなにも遅いのかを調べてみました。そういえばPython関係のブログを始めて1年ほど経ちますが、処理速度については全く意識していませんでした。
Pythonは特にfor文といったループ系の文が遅い遅いと世間で言われています。
でもなんで遅いのでしょう?
正直僕はそんなに情報工学に詳しくないので、中々イメージできていませんでしたが、以下に理解の参考となったブログがありましたのでいくつかメモしておきます。
“GIL(グローバルインタプリタロック)であるため”
POSTD:なぜPythonはこんなにも遅いのか?
“インタプリタ言語で、コンパイルされないため”
“動的型付き言語であるため”
…Pythonが遅い理由には色々な要因が考えられるみたいですが、動的型付き言語であるというのが一番あやしいようです。
for文では逐一型チェックをしているようです。
「Pythonではfor文を書いたら負け」という言葉も良く聞きます。できるだけnumpyの行列演算で済ますというのが定石です。
しかし、漸化式を解く等、for文を使わないと厳しい場面もあります。
今回はfor文を書いてもそんなに負けない方法としてNumbaを使ってみます。
Numbaを使ってPythonコードを高速化する方法
初心者のPythonコード高速化にNumbaを勧める理由
PythonはかのNumpyや機械学習関係を始めとした特殊な外部ライブラリが豊富です。そのため、他の型宣言を必要とした高速な言語を中々使いたくない人が沢山いらっしゃいます。
そして、Pythonコードの一部が遅いという欠点を補うライブラリも様々あることがPythonの人気の1つとも言えます。
高速化の代表格にCythonというものがあります。CythonはコードをC/C++に変換することによって高速化するものですが、Pythonicな書き方といってもC/C++の知識は必須であったり、割と「手軽にはやくしたい!」という初心者にはハードルが高かったりします。
今回紹介するNumbaはJITコンパイルという手法を用いた高速化を行うライブラリです。
JITとは、Just In Timeの略で、JITコンパイルはプログラムの実行時に、予め中間コードにコンパイルしてから実行することを意味します。
そしてNumbaはおそろしく手軽に高速化を試すことができます。それでは、早速Numbaのインストールを行って実際に高速化を体験してみたいと思います。
Numbaのインストール
Numbaは以下のコードでpipインストールが可能です。
|
1 |
python -m pip install numba |
インストールはすぐに終わるので、以下の検証用コードで試してみましょう。
関数の前に「@jit」と書くだけでPythonコードの高速化を試すことができます。
フィボナッチ数列で検証
for文の速度変化を試すのにうってつけの計算の1つに、フィボナッチ数列を求める漸化式があります。
この数列は,
...となり、\(f_{n}=f_{n-1}+f_{n-2}\)で計算できます。
素晴らしい一般項はあるのですが、あえて漸化式をfor文で解きます。Pythonでfor文を書いて負けてみます。
JIT無しの速度
フィボナッチ数のwikipediaページにも載っているPythonコードは以下です。
計算時間をimportしたtimeで計測しながら、無駄に100万項求めます。
|
1 2 3 4 5 6 7 8 9 10 11 12 |
import time def fibonacci_loop(n): a, b = 1, 0 for _ in range(n): a, b = b, a + b t0 = time.time() n = 1000000 fibonacci_loop(n) t1 = time.time() print('Calculation time=', float(t1 - t0), '[s]') |
CPUは1.6GHz、RAMは8GBの弊PCで上記コードを実行すると、以下の結果を得ます。26[s]以上もかかっていますね。
|
1 |
Calculation time= 26.85403084754944 [s] |
JIT有りの速度
それでは、次はJITを使ってみましょう。使い方は簡単。numbaからjitをimportし、def関数の前に@jitを付けているだけです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import time from numba import jit @jit def fibonacci_loop(n): a, b = 1, 0 for _ in range(n): a, b = b, a + b t0 = time.time() n = 1000000 fibonacci_loop(n) t1 = time.time() print('Calculation time=', float(t1 - t0), '[s]') |
計測結果はなんと0.6[s]ほどになりました。先ほどの26[s]と比べると43.6倍の高速化がなされたこととなります!
|
1 |
Calculation time= 0.6165540218353271 [s] |
マンデルブロ集合で検証
フィボナッチ数列だけでは月並みなので、マンデルブロ集合の計算でも試してみます。マンデルブロ集合については「Pythonで描くマンデルブロ集合!フラクタルの旅を体感してみる」の記事で紹介していますので、ご興味がありましたら是非読んでみて下さい。
以下にマンデルブロ集合を描画するコードを再掲します。ここではJIT有りの場合のみを記載します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 |
import numpy as np from matplotlib import pyplot as plt from matplotlib.colors import Normalize # カラーマップを自在に操作するために必要 from numba import jit # これが無いとおそろしく計算時間がかかる import time # 計算時間を見るために必要 t0 = time.time() @jit # NumbaによるJust In Time Compileを実行 def mandelbrot(c_real, c_imag, n_max): Re, Im = np.meshgrid(c_real, c_imag) # ReとImの組み合わせを計算 n_grid = len(Re.ravel()) # 組み合わせの総数 z = np.zeros(n_grid) # マンデルブロ集合のデータ格納用空配列 # zにマンデルブロ集合に属するか否かのデータを格納していくループ for i in range(n_grid): c = complex(Re.ravel()[i], Im.ravel()[i]) # 複素数cを定義 # イタレーション回数nと複素数z0を初期化 n = 0 z0 = complex(0, 0) # z0が無限大になるか、最大イタレーション数になるまでループする while np.abs(z0) < 1e20 and not n == n_max: z0 = z0 ** 2 + c # 漸化式を計算 n += 1 # イタレーション数を増分 # z0が無限大に発散する場合はn, 収束する場合は0を格納 if n == n_max: z[i] = 0 else: z[i] = n # 計算の進捗度をモニター(毎ループだと計算が遅くなるため) if i % 100000 == 0: print(i, '/',n_grid, (i/n_grid)*100) z = np.reshape(z, Re.shape) # 2次元配列(画像表示用)にリシェイプ z = z[::-1] # imshow()で上下逆になるので予め上下反転 return z # 水平方向h(実部Re)と垂直方向v(虚部Im)の範囲を決める h1 = -2 h2 = 0.5 v1 = -1.2 v2 = 1.2 # 分解能を設定 resolution = 1000 # 実部と虚部の軸データ配列、最大イタレーション数を設定 c_real = np.linspace(h1, h2, resolution) c_imag = np.linspace(v1, v2, resolution) n_max = 100 # 関数を実行し画像を得る z = mandelbrot(c_real, c_imag, n_max) t1 = time.time() print('Calculation time=', float(t1 - t0), '[s]') # ここからグラフ表示---------------------------------------- fig = plt.figure() ax1 = fig.add_subplot(111) ax1.set_xlabel('Re') ax1.set_ylabel('Im') mappable = ax1.imshow(z, cmap='jet', norm=Normalize(vmin=0, vmax=n_max), extent=[h1, h2, v1, v2]) cbar = plt.colorbar(mappable=mappable, ax=ax1) cbar.set_label('Iteration until divergence') cbar.set_clim(0, n_max) ax1.axis('off') plt.tight_layout() plt.show() plt.close() # ---------------------------------------------------------- |
JIT無しの速度
まずはJIT無しの結果です。漸化式をforループで解くのに289[s]もかかっています。
|
1 2 3 4 5 6 7 8 9 10 11 |
0 / 1000000 0.0 100000 / 1000000 10.0 200000 / 1000000 20.0 300000 / 1000000 30.0 400000 / 1000000 40.0 500000 / 1000000 50.0 600000 / 1000000 60.0 700000 / 1000000 70.0 800000 / 1000000 80.0 900000 / 1000000 90.0 Calculation time= 289.0451829433441 [s] |
JIT有りの速度
次に、JIT有りの結果です。なんと289[s]がわずか7[s]ほどになりました!41倍の高速化です!
|
1 2 3 4 5 6 7 8 9 10 11 |
0 / 1000000 0.0 100000 / 1000000 10.0 200000 / 1000000 20.0 300000 / 1000000 30.0 400000 / 1000000 40.0 500000 / 1000000 50.0 600000 / 1000000 60.0 700000 / 1000000 70.0 800000 / 1000000 80.0 900000 / 1000000 90.0 Calculation time= 7.029422283172607 [s] |
ちなみに、マンデルブロ集合を計算すると、以下のように美麗な画像を得ることができます。条件をいくつも変更しながら描画を試す時に長時間待ちたくないので、JITによる高速化は大変ありがたいですね。
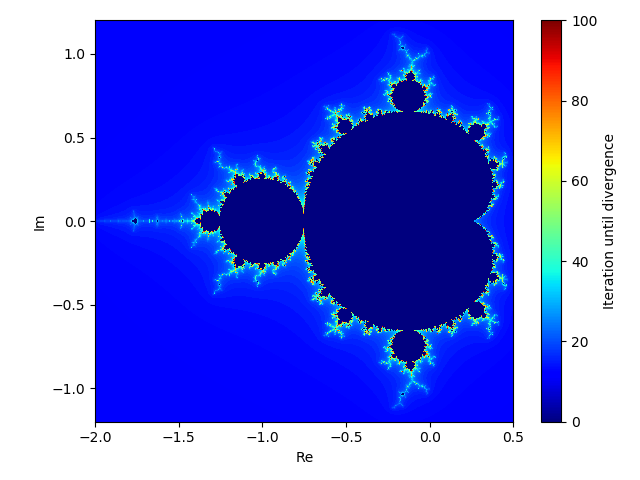
両方とも40倍程度の高速化が実現されました!40という数字は共通でしたが、何か理由があるのかな?
まとめ
本記事ではPythonのネックとなっているループ処理時間を高速化する方法として、NumbaというライブラリのJITを紹介しました。
forループでかかれたフィボナッチ数列とマンデルブロ集合を得る漸化式に対してJITを使うことで、共に約40倍の高速化を行うことができました。
Pythonでコードを書くにあたり、NumbaのJITを使った高速化手法は簡単なのに強力な武器になりますね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
z0が無限ではなくて2を超えた時にしたほうが計算がはやくなりますよ
アドバイスありがとうございます!
高速化のテクニックとして元の記事に一言追記しておきました。
https://watlab-blog.com/2020/05/23/mandelbrot-set/