複素力学系の範囲に大変不思議な図形を描画する「マンデルブロ集合」というものがあります。ここではPythonを使って複素数の漸化式をシミュレートし、マンデルブロ集合を実際にプロットしてみました。
こんにちは。wat(@watlablog)です。ここでは芸術的なフラクタル図形であるマンデルブロ集合をPythonで計算・描画してみます！
マンデルブロ集合の概要
漸化式
マンデルブロ集合(Mandelbrot set)とは、数学者ブノワ・マンデルブロによって研究された集合で、以下の漸化式(1)を使って求めるものです。
\[
\begin{align}
z_{n+1}&=z_{n}^{2}+c\\
z_{0}&=0
\end{align}
\tag{1}
\]
漸化式とは、前の項を使って次の項を説明した式のことで、当WATLABブログでは「Python/sympyとnumpyで書くニュートン-ラフソン法」でも出て来ました。
ここで、式中の\(z\)も\(c\)も複素数であり、\(z\)の初期値\(z_{0}=0\)として\(n→∞\)と反復計算をさせた時に、\(z\)が無限大に発散しない点の集合をマンデルブロ集合と呼びます。
漸化式の収束と発散をプログラムで確認
漸化式が発散するとかしないとか、これからマンデルブロ集合を描く前に複素数の式を扱うイメージを固めておきましょう。
収束の例
まずは収束のパターンを見てみましょう。
以下のコードは漸化式(1)の複素数の実部=0.1, 虚部=0.1と設定し、z0=0からwhileループで計算を進めるものです。
ループ停止条件はzの絶対値が∞(inf)になった時と、ループ回数nが設定した反復回数n_maxに至った時です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np z0 = complex(0, 0) c = complex(0.1, 0.1) n_max = 100 n = 0 while np.abs(z0) < np.inf and not n == n_max: z0 = z0 ** 2 + c n += 1 print(z0) if n == n_max: print('収束しました。') else: print(n, '回のループで発散しました。') |
infではなく2を閾値にするという、高速化しながら同等の結果を得る方法もあります！
上記コードをPythonで実行すると以下の結果を得ます。
徐々に数値が増えていき、ある所から同じ数値しか出なくなりました。
このようにだんだんとある値に向かって変化がなくなることを収束と表現します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 |
(0.1+0.1j) (0.1+0.12000000000000001j) (0.0956+0.12400000000000001j) (0.09376336+0.12370880000000001j) (0.09348770048104961+0.123198705499136j) . . . (0.09362728698078197+0.12303975734127459j) (0.09362728698078197+0.12303975734127459j) (0.09362728698078197+0.12303975734127459j) (0.09362728698078197+0.12303975734127459j) 収束しました。 |
発散の例
続いて発散の例を示します。
先ほどのコード内cの値において、実部=-1, 虚部=0.5としてみます。
|
1 |
c = complex(-1, 0.5) |
このコードを実行すると以下の結果を得ます。
今回は先ほどと異なり、数値がどんどん大きくなって、最終的にはわずか15回のループでコンピュータが値を表現できなくなるほどになりました（nan値）。
このように、値が正負問わず無限大に向かうことを発散と表現します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
(-1+0.5j) (-0.25-0.5j) (-1.1875+0.75j) (-0.15234375-1.28125j) (-2.6183929443359375+0.890380859375j) . . . (-9.80419612735662e+25+3.762837584761331e+25j) (8.196331501438207e+51-7.378319535277796e+51j) (1.2740250916806342e+103-1.2095030566934862e+104j) (-1.446666244808568e+208-3.081874485383852e+207j) (nan+nanj) 15 回のループで発散しました。 |
複素平面全体で収束と発散を見てみる
先ほどまでの収束と発散は実部を横軸に、虚部を縦軸にとった複素平面で表現すると以下の図のようになります。複素平面の各座標で発散するかどうかが変わるということですね。
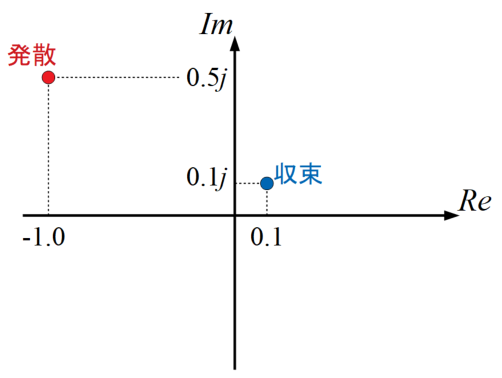
この収束と発散の調査を全ての複素平面範囲で行った結果が以下の図です。収束した座標は0で黒くし、発散した座標は発散までに何回反復計算をしたかに応じて色を変えて表現しています。
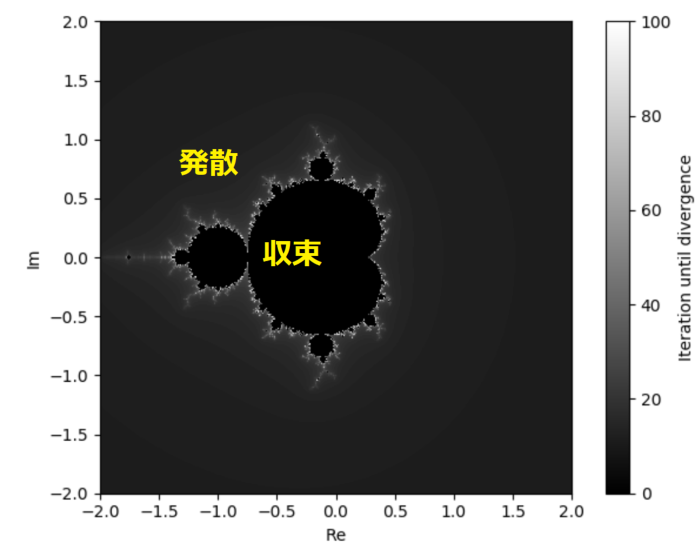
図の中央付近に収束した黒色が特徴的な形をもって集合していますが、この集合こそがマンデルブロ集合と呼ばれるものです。
Pythonでマンデルブロ集合を描くコード
準備：Numba
マンデルブロ集合の計算はコンピュータのベンチマークテストに利用されるほど重い計算になります。
Pythonは動的型付機能を持っており、インタプリタ言語なので、特にforループにおいて毎ループで行われている型チェックが重く、C言語に代表されるような実行前にコンパイルをする他言語と比べだいぶ遅いです。
しかし、Numbaというライブラリを使えば、プログラムによっては大きく計算速度を上げることができます。
今回のマンデルブロ集合を綺麗に描くためにはある程度の計算量が必要ですので、事前に使えるよう準備が必要です。
※Numbaについては「NumbaのJITでPythonを高速化したら40倍も速くなった」にまとめましたので、是非ご覧下さい。
全コード
以下にマンデルブロ集合を描く全コードです。
詳細はコード内にコメントを記載しましたので、是非ご覧ください。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 |
import numpy as np from matplotlib import pyplot as plt from matplotlib.colors import Normalize # カラーマップを自在に操作するために必要 from numba import jit # これが無いとおそろしく計算時間がかかる import time # 計算時間を見るために必要 t0 = time.time() @jit # NumbaによるJust In Time Compileを実行 def mandelbrot(c_real, c_imag, n_max): Re, Im = np.meshgrid(c_real, c_imag) # ReとImの組み合わせを計算 n_grid = len(Re.ravel()) # 組み合わせの総数 z = np.zeros(n_grid) # マンデルブロ集合のデータ格納用空配列 # zにマンデルブロ集合に属するか否かのデータを格納していくループ for i in range(n_grid): c = complex(Re.ravel()[i], Im.ravel()[i]) # 複素数cを定義 # イタレーション回数nと複素数z0を初期化 n = 0 z0 = complex(0, 0) # z0が無限大になるか、最大イタレーション数になるまでループする while np.abs(z0) < np.inf and not n == n_max: z0 = z0 ** 2 + c # 漸化式を計算 n += 1 # イタレーション数を増分 # z0が無限大に発散する場合はn, 収束する場合は0を格納 if n == n_max: z[i] = 0 else: z[i] = n # 計算の進捗度をモニター(毎ループだと計算が遅くなるため) if i % 100000 == 0: print(i, '/',n_grid, (i/n_grid)*100) z = np.reshape(z, Re.shape) # 2次元配列(画像表示用)にリシェイプ z = z[::-1] # imshow()で上下逆になるので予め上下反転 return z # 水平方向h(実部Re)と垂直方向v(虚部Im)の範囲を決める h1 = -2 h2 = 0.5 v1 = -1.2 v2 = 1.2 # 分解能を設定 resolution = 4000 # 実部と虚部の軸データ配列、最大イタレーション数を設定 c_real = np.linspace(h1, h2, resolution) c_imag = np.linspace(v1, v2, resolution) n_max = 100 # 関数を実行し画像を得る z = mandelbrot(c_real, c_imag, n_max) t1 = time.time() print('Calculation time=', float(t1 - t0), '[s]') # ここからグラフ表示---------------------------------------- fig = plt.figure() ax1 = fig.add_subplot(111) ax1.set_xlabel('Re') ax1.set_ylabel('Im') mappable = ax1.imshow(z, cmap='jet', norm=Normalize(vmin=0, vmax=n_max), extent=[h1, h2, v1, v2]) cbar = plt.colorbar(mappable=mappable, ax=ax1) cbar.set_label('Iteration until divergence') cbar.set_clim(0, n_max) plt.tight_layout() plt.show() plt.close() # ---------------------------------------------------------- |
np.meshgridとNumbaのJITを併用しているのでワーニングが出ると思いますが、特に問題はなさそうです。色はcmap='jet'を使っています。
実行結果：フラクタルを旅する
マンデルブロ集合の全体
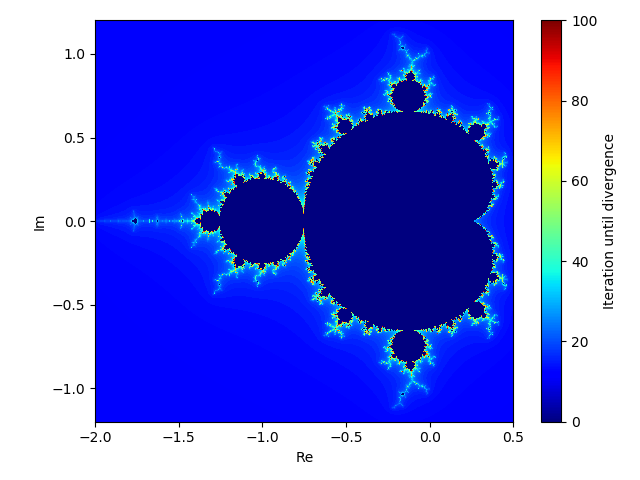
以下が上記コードの実行結果です。
まずは収束している範囲全体を網羅するようh1, h2, v1, v2を設定しました。
よくネットで検索すると出てくる代表的な図です。なんとも不思議！
拡大図1
Re=-1.77, Im=0周り(先端部と呼んでも良い？)をもっと拡大した結果が下図です。なんと、拡大しても先ほどの全体図と同じような模様がまた出て来ました！
良く見ると収束と発散の境界部を見ても同じような模様が多数あります。
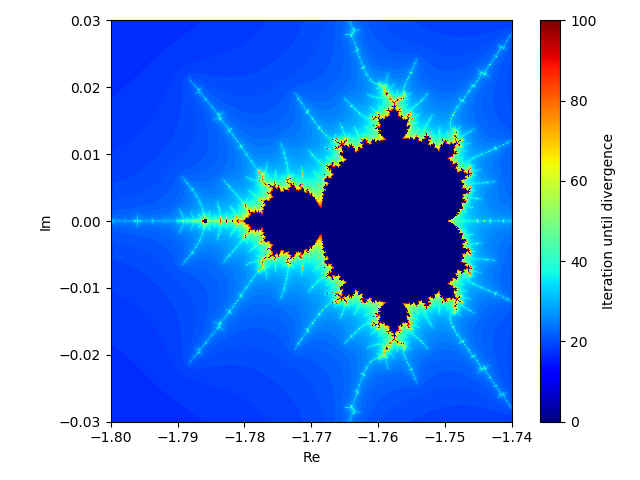
このように、図形の全体と部分が自己相似になっているものをフラクタルと呼びますが、このマンデルブロ集合はまさにそうなっています。
（フラクタルという幾何学概念もブノワ・マンデルブロが導入したそうです！）
拡大図2
続いてもっと細かく、Re=-1.776, Im=0.007周り、集合境界の端っこの部分も見てみましょう。
これまた芸術的な模様となっており、まるで生物・植物や宇宙に関する教科書で見たような図形です！
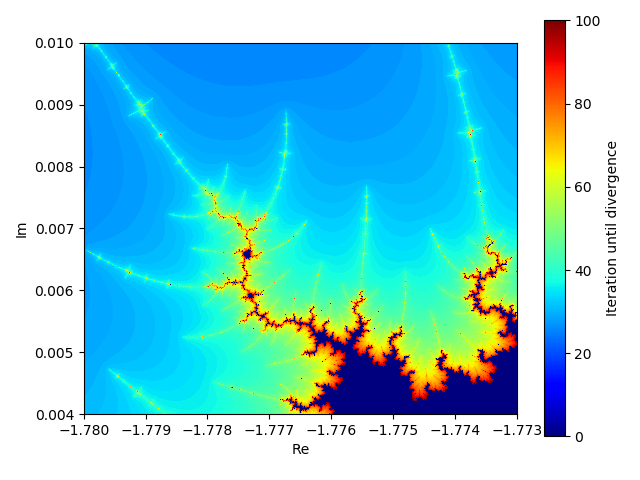
拡大図3
下図はさらにRe=-1.778, Im=0.0074周り、先ほどの図で線みたいになっている部分を拡大してみた図です。まだまだ収束している部分がありますね。
図の中央ちょっと右下に少し大きい収束地があります。
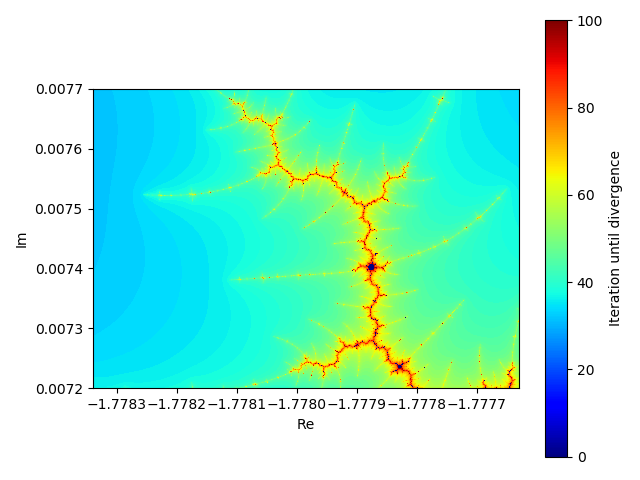
拡大図4
ちょっと小数点以下の桁が増えて来ましたが、先ほどの黒い所をさらに拡大してみた結果が下図です。コンピュータ上ではいずれ数値で表現できない桁数になりますが、数学的には無限にフラクタル構造が続いているようですね！
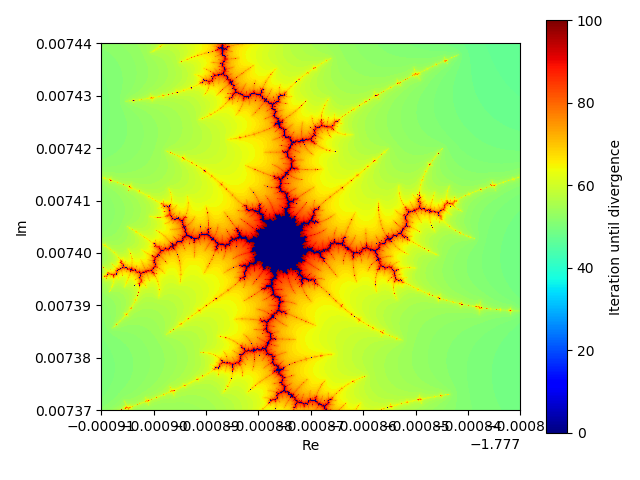
こっちはどうなっているんだろう？あっちを拡大したら何が見えるんだろう！…と複素平面中の不思議な模様を探索していく様はまるで見知らぬ土地を旅しているみたいです。是非皆様もお持ちの環境で実際に自分でマンデルブロ集合を描いてみて下さい！
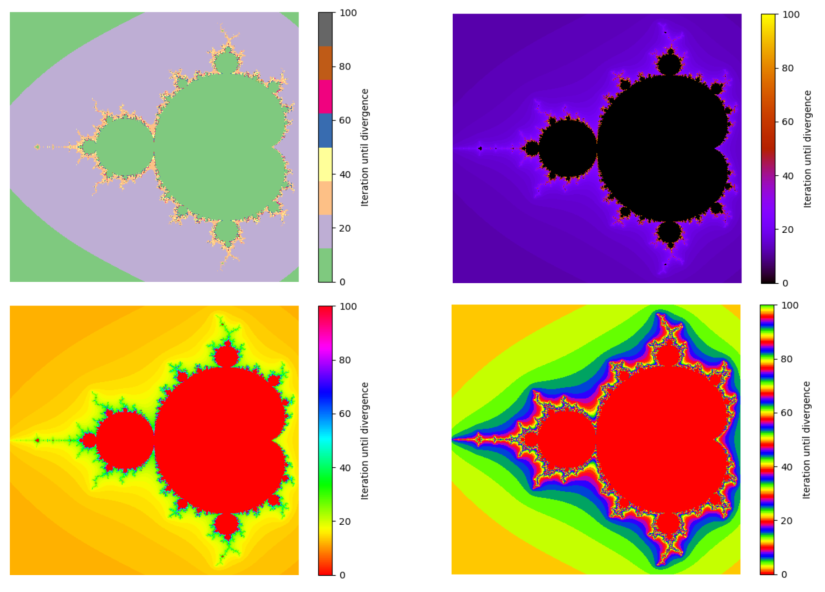
cmapギャラリー
imshowで指定しているcmapを変えるだけでも、以下の図のようにマンデルブロ集合の図の印象を大きく変えることが出来ます。
是非matplotlibの公式ページで紹介されているcmapをお試し下さい。
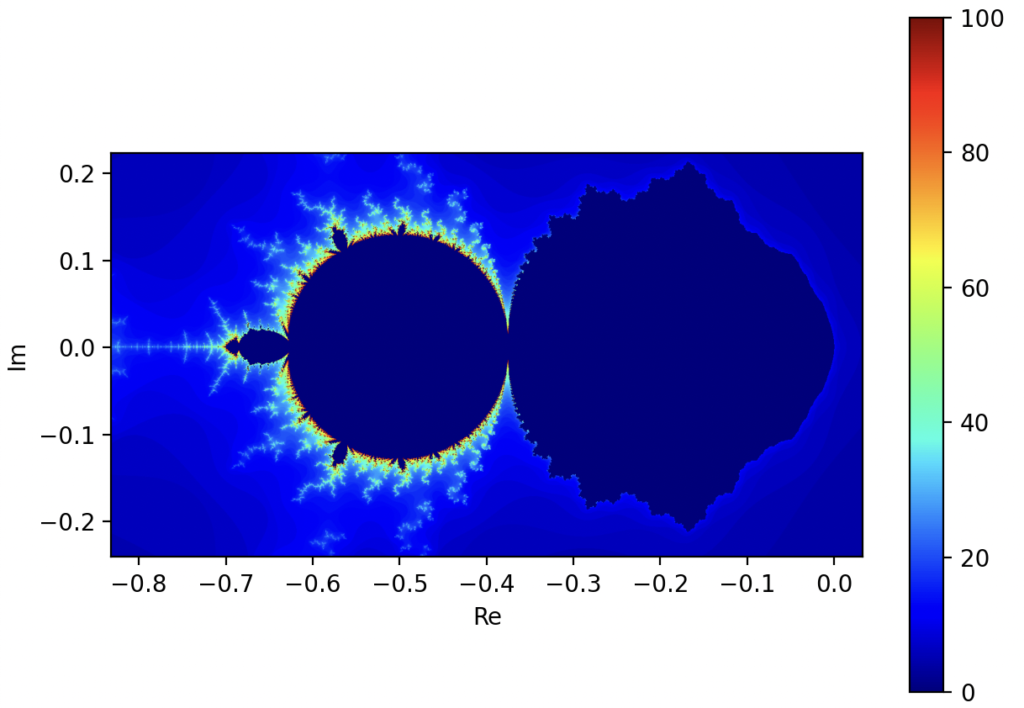
まとめ
本記事ではPythonを使って有名なマンデルブロ集合を描画してみました。
Pythonのforループは大変遅く、マンデルブロ集合を描く場合はNumba等をはじめとした高速化を行うことがオススメです。
他にもCythonといったライブラリもあるようなので、本計算はその手の高速化手法を試すのにピッタリかも知れません。
これが\(z_{n+1}=z_{n}^2+c\)という単純な漸化式の収束判定から出て来たとは未だに信じられません…！
今回は芸術会！世の中のフラクタル作家の気持ちが少しわかったような気がします！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント