ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
フーリエ変換は1次元(1D)の信号に対してかけるのが一般的ですが、2次元(2D)信号にかけることで画像のフィルタリングに応用可能です。ここではPython/Numpyを使った2Dフーリエ変換の方法を紹介します。
こんにちは。wat(@watlablog)です。今回は画像のフィルタリングが可能な2Dフーリエ変換コードを学びます！
フーリエ変換で出来る事の概要
1D信号の場合
2D信号のフーリエ変換を説明する前に、まずは基本の1D信号のフーリエ変換をおさらいしておきましょう。
1D信号とはある1つの軸に対し値がただ1つ決まる信号の事であり、例えば横軸に時間をとって加速度を計測したデータ等は1D信号に当たります。
実際にそのようなデータを計測すると、多くの場合が複雑な振動現象となっているため、人間が理解できるように時間領域を周波数領域に変換する計算を行います。この変換の事をフーリエ変換と呼びます。
離散データの場合は離散フーリエ変換(DFT：Discrete Fourier Transform)を使い、特にデータ数を\(2^{n}\)にした場合に高速に処理する高速フーリエ変換(FFT:Fast Fourier Transform)というものもあります。
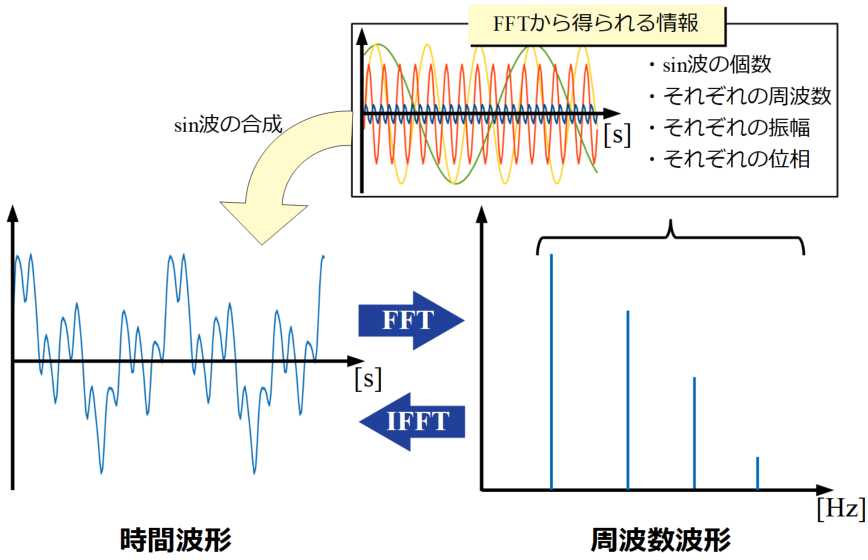
下図のようにフーリエ変換を行うことで、複雑な時間波形にいくつの周波数成分がどれだけ入っているかを分析することができ、現象の理解やノイズ除去といった使い方が可能です。
1D信号の場合のフーリエ変換については、当ブログ「信号処理カテゴリ」の以下の記事が関連しています。Pythonコードも記載していますので、ご興味のある方は是非ご覧下さい。
「PythonでFFT!SciPyのFFTまとめ」
「PythonでFFTとIFFT!逆フーリエ変換で時間波形を作る」
2D信号におけるフーリエ変換とは？
2D信号の場合のフーリエ変換も1D信号の場合と全く同じ考え方をします。
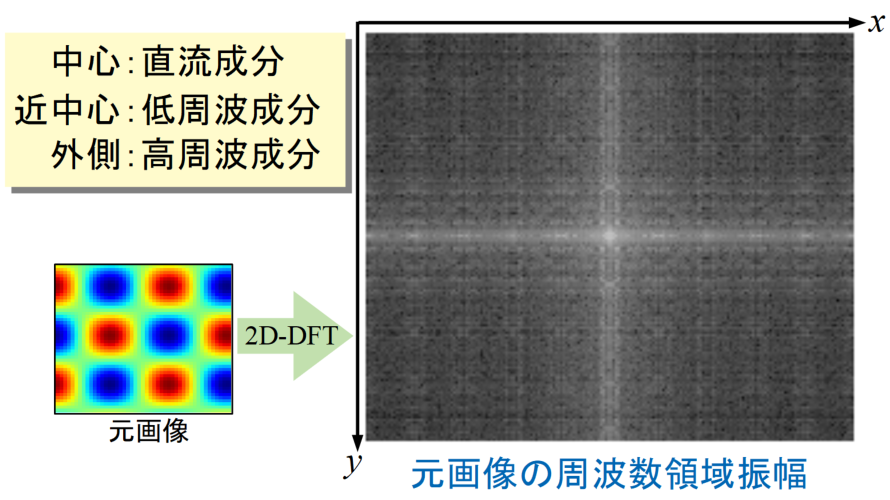
以下に元画像と元画像を2D離散フーリエ変換(2D-DFT)した図を示します。このように画像をフーリエ変換することで、画像の周波数領域輝度値を見ることができます。
この画像の周波数領域は、中心が直流(DC)成分、中心に近い部分は低周波成分、外側にいくほど高周波成分であることを意味します。
2Dフーリエ変換で画像のフィルタリングが出来る
2Dフーリエ変換後の振幅画像は、ただ見てるだけではよく分からない画像に過ぎません。この周波数領域の画像を使ってよく行われる処理は、画像のフィルタリングです。
以下の図は2Dフーリエ変換を利用したフィルタリングの例です。
(a)の元画像(ここではグレースケール画像)に対し、(b)で2Dフーリエ変換を行っています。ここで(c)として直流成分付近を黒く(0にする)してから(d)と2D逆フーリエ変換を行うと、画像に対してハイパスフィルタをかけたことと同じになります。
今回はこの画像フィルタリングコードをPythonで書いてみます。
2Dフーリエ変換により画像フィルタリングをするPythonコード
以下に2Dフーリエ変換をして画像フィルタリングをするPythonコードを示します。詳細は以下のコード内コメントに記載しました。
以下にプログラムで使用するサンプル画像を準備しました。コードの検証にダウンロードしてお使いください。
※ちなみにこの画像は筆者お気に入りの関数\(z = \sin x + \cos y\)をmatplotlibで3Dプロットし、cmap='jet'でコンター表示させ上から見た図です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import cv2 import numpy as np from matplotlib import pyplot as plt # 画像を読み込み、2Dフーリエ変換をする img = cv2.imread('sample-img-fft.png', 0) # 画像をグレースケールで読み込み f = np.fft.fft2(img) # 2Dフーリエ変換 f_shift = np.fft.fftshift(f) # 直流成分を画像中心に移動させるためN/2シフトさせる mag = 20 * np.log(np.abs(f_shift)) # 振幅成分を計算 # 周波数領域にマスクをかける rows, cols = img.shape # 画像サイズを取得 crow, ccol = int(rows / 2), int(cols / 2) # 画像中心を計算 mask = 30 # マスクのサイズ f_shift[crow-mask:crow+mask, ccol-mask:ccol+mask] = 0 # 2D逆フーリエ変換によりフィルタリング後の画像を得る f_ishift = np.fft.ifftshift(f_shift) # シフト分を元に戻す img_back = np.fft.ifft2(f_ishift) # 逆フーリエ変換 img_back = np.abs(img_back) # 実部を計算する # ここからグラフ表示 fig = plt.figure(figsize=(10, 3)) ax1 = fig.add_subplot(131) ax2 = fig.add_subplot(132) ax3 = fig.add_subplot(133) ax1.imshow(img, cmap='gray') ax2.imshow(mag, cmap='gray') ax3.imshow(img_back, cmap='gray') ax1.axis('off') ax2.axis('off') ax3.axis('off') plt.tight_layout() plt.show() plt.close() |
以下が実行結果です。左が元画像、真ん中が2Dフーリエ変換後の周波数領域振幅画像、右がフィルタリング後の画像です。
まとめ
本記事では1Dフーリエ変換をおさらいし、画像に対する2Dフーリエ変換によるハイパスフィルタリングの方法を説明しました。
また、実際に画像フィルタリングを行うPythonコードをNumpyで書いてみました。
2Dフーリエ変換もPythonであれば簡単に計算できることがわかりました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
元画像”sample.png”のリンクを示していただけるとありがたいです。
ご要望ありがとうございます。
コード部分の上にダウンロードボタンを用意してみました。
是非ご活用ください。
ありがとうございます。助かります。