
ペアプロット(行列散布図)は多変量データの良い可視化手法です。seabornなら一発ですが、細かい可視化条件を付け難いため、ここではPythonのmatplotlibで自作し、相関係数によって背景色が変わるようにしてみました。
こんにちは。wat(@watlablog)です。ここではseabornを使わずにカスタマイズしたペアプロットを作成する方法を紹介します!
ペアプロットの概要と自作する理由
seabornを使えば簡単にプロット可能
ペアプロット(行列散布図)とは、大量の変数列があるデータに対し、全ての変数の組み合わせ毎に相関関係を見るためのプロットです。
当WATLABブログでは「Python/seabornで行列散布図!ペアプロット方法と設定」という記事でPandasデータフレームで構成されたデータ群のペアプロット法を紹介しました。
上記記事では、以下の図のような結果を得ることができます。
図は対角線上にヒストグラム(histogram)、その他の要素はそれぞれの横変数と縦変数をクロスさせた散布図(scatter plot)を並べるというものです。
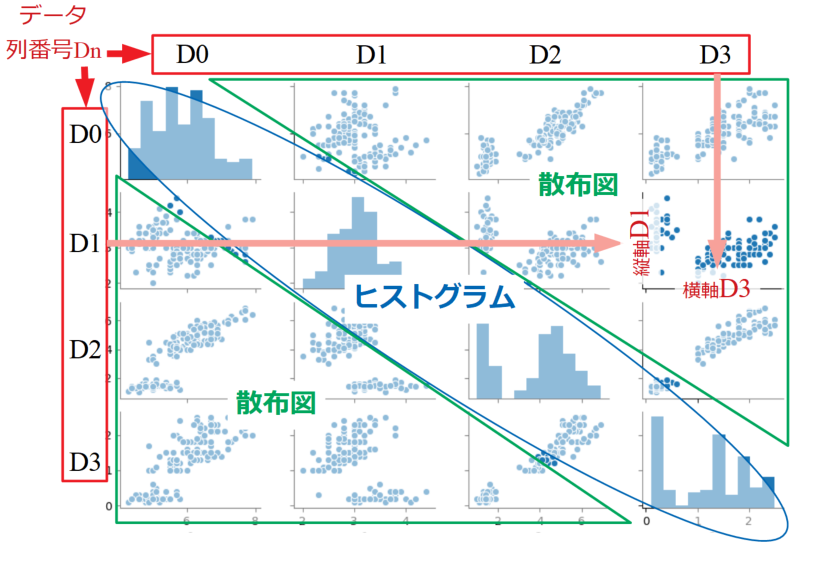
このように俯瞰するとどの変数とどの変数がどれだけ相関があるのかといった情報をひと目で得ることが可能です。
そう…この程度の変数量であれば!
以下の図はscikit-learnにプリセットされている乳がんに関するデータセット(dataset.load_breast_cancer())をペアプロットしたものです。

(…圧倒)
変数の数は30程度ですが、ペアプロットにすると\(30^{2}\)のグラフが作成されるので、変数が多いと正直ここから何を読み取れば良いかがわかりません。
ペアプロットの目的から考え直そう!
多変量のデータを分析して何がしたい?
そもそも、ペアプロットは相関関係をざっくりと確認することが目的なので、個人的には多変量データの場合はペアプロットを使って細かく数値を分析する必要はないと考えます。
もちろん特徴量エンジニアリングとして細かい分析ができることに越したことはありませんが、その場合はペアプロットではなく別の手法を使った方が良いと思います。
多変量データを分析することで、各変数の重要度・寄与度分析や回帰モデルを生成することが出来ます。
しかしながら、変数が増えてくると多重共線性(マルチコ)という問題がおきやすく、何も考えずデータをそのまま学習に使ってしまうと予測精度が著しく落ちてしまうといったことになります。
多変量解析における注意点等の話は、「Python機械学習!scikit-learnによる重回帰分析」に少し記載しましたので是非参考にしてみて下さい。
相関係数が重要ならそれも可視化しよう!
ペアプロットの強みは、大まかに相関関係を把握できることなので、直接それをマトリクスにしてみようと思ったのがこの記事を書き始めた発端です。
今回は以下の図のようにペアプロットの各散布図に相関係数による色付けをしてみました。

このようなことが出来れば、下図のように決定係数\(R^{2}=0.6\)以上の散布図だけ赤くマーキング…といったことも可能になります。
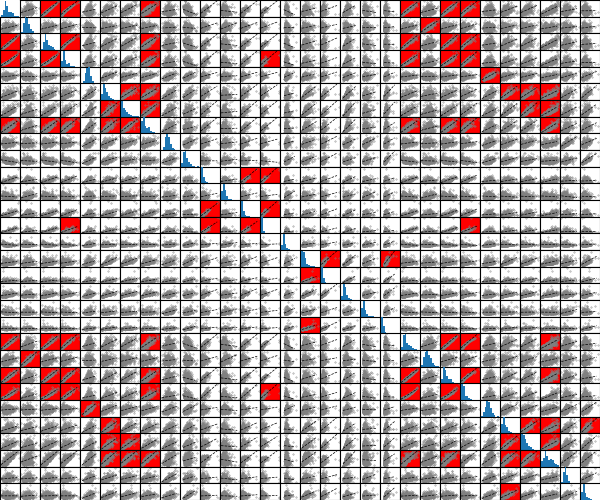
これなら少しは見やすいかも知れない!
seabornだと細かいカスタマイズが難しい
あとはこれを実現するコードをサクっとseabornの引数指定とかでいければ問題なかったのですが、中々公式ドキュメント見てもよくわかりませんでした。
seabornのpairplotは全体のグラフに対してクラスで色分けしたり、Pandasデータフレームのインデックスを扱えたりする所は得意なのですが、ある座標のプロパティだけを変更…といった細かい作業は不得意だと感じます(僕が探せなかっただけかも知れませんが)。
そのため今回はグラフ描画機能はmatplotlib、データ処理系はPandasとかNumpyといった良く使うものだけでペアプロットをしてカスタマイズしやすくしてみました。
Pythonでペアプロットを自作してカスタマイズするコード
全コード:相関係数ヒートマップペアプロット
以下のコードは相関係数Rをカラーマップの0から255のデータ範囲に正規化(スケーリング)して背景色にするコードです。
この見方が世の中にあるかはわかりませんが、相関係数ヒートマップペアプロット(R-HP:R-Heatmap Pairplot)と勝手に名前を付けてしまいます。
詳細はコード内にコメントを書きましたので、参考にしてみて下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
import numpy as np import pandas as pd from matplotlib import pyplot as plt from sklearn import datasets # データを用意する ds = datasets.load_breast_cancer() # scikit-learnのdatasetsを読み込む df = pd.DataFrame(ds.data) # pandasのデータフレーム構造に変換する max_col = len(df.columns) # 変数の数 fig = plt.figure(figsize=(6, 5)) # プロットサイズを指定してfigオブジェクト生成 cm = plt.get_cmap('coolwarm') # カラーマップ # 変数の数の2乗分ループを回す for i in range(max_col): for j in range(max_col): y = df[i] # 縦軸値を順次抽出 # iとjが同じ時はヒストグラムを計算する if i == j: ax = fig.add_axes([j/max_col, # 1プロットの左下のx座標(figサイズが1) (max_col-(i+1))/max_col, # 1プロットの左下のy座標(figサイズが1) 1/max_col, # 1プロットの横幅 1/max_col]) # 1プロットの高さ ax.hist(y) # ヒストグラムをプロット ax.axis('off') # 軸はじゃまなので消す else: x = df[j] # 横軸値を順次抽出 coe = np.polyfit(x, y, 1) # 回帰直線にフィットさせ、回帰パラメータを計算 corr = np.corrcoef(x, y) # 相関係数を計算 x_reg = np.arange(np.min(x), # 回帰直線の横軸(データ範囲のみ) np.max(x), (np.max(x)-np.min(x))/10) y_reg = coe[0] * x_reg + coe[1] # 回帰パラメータ(傾きと切片)で直線y値計算 r_norm = int(((corr[0, 1]+1)/2) * 255) # 相関係数をカラーマップの範囲(0-255)に正規化 ax = fig.add_axes([j/max_col, # ヒストグラムの時(上コメント)と同様 (max_col-(i+1))/max_col, 1 / max_col, 1 / max_col]) ax.scatter(x, y, s=0.1, color='gray') # 散布図をプロット ax.plot(x_reg, y_reg, # 回帰直線をプロット linestyle='dashed', color='black', lw=0.5) ax.set_xticks([]) # x軸ラベルだけを消す ax.set_yticks([]) # y軸ラベルだけを消す ax.set_facecolor(cm(r_norm)) # プロットの背景色をカラーマップから抽出 # グラフを表示する。 plt.show() plt.close() |
このコードは上で紹介した以下の図が表示されます。もしPCが重いと感じる人はまずはirisデータセットとかでお試ししてみると良いかも知れません。

全コード:\(R^{2}\)閾値ペアプロット
続いて以下のコードは決定係数\(R^{2}\)で散布図を赤でマーキングするコードです。
こちらは仮に\(R^{2}\)閾値ペアプロット(R2TP:\(R^{2}\)-Threshold Pairplot)と呼んでみましょう(既にあったらすみません)。
こちらも詳細はコード内のコメントを参照下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import numpy as np import pandas as pd from matplotlib import pyplot as plt from sklearn import datasets # データを用意する ds = datasets.load_breast_cancer() # scikit-learnのdatasetsを読み込む df = pd.DataFrame(ds.data) # pandasのデータフレーム構造に変換する max_col = len(df.columns) # 変数の数 fig = plt.figure(figsize=(6, 5)) # プロットサイズを指定してfigオブジェクト生成 threshold = 0.6 # 散布図にマーキングする閾値 # 変数の数の2乗分ループを回す for i in range(max_col): for j in range(max_col): y = df[i] # 縦軸値を順次抽出 # iとjが同じ時はヒストグラムを計算する if i == j: ax = fig.add_axes([j/max_col, # 1プロットの左下のx座標(figサイズが1) (max_col-(i+1))/max_col, # 1プロットの左下のy座標(figサイズが1) 1/max_col, # 1プロットの横幅 1/max_col]) # 1プロットの高さ ax.hist(y) # ヒストグラムをプロット ax.axis('off') # 軸はじゃまなので消す else: x = df[j] # 横軸値を順次抽出 coe = np.polyfit(x, y, 1) # 回帰直線にフィットさせ、回帰パラメータを計算 corr = np.corrcoef(x, y) # 相関係数を計算 x_reg = np.arange(np.min(x), # 回帰直線の横軸(データ範囲のみ) np.max(x), (np.max(x)-np.min(x))/10) y_reg = coe[0] * x_reg + coe[1] # 回帰パラメータ(傾きと切片)で直線y値計算 ax = fig.add_axes([j/max_col, # ヒストグラムの時(上コメント)と同様 (max_col-(i+1))/max_col, 1 / max_col, 1 / max_col]) ax.scatter(x, y, s=0.1, color='gray') # 散布図をプロット ax.plot(x_reg, y_reg, # 回帰直線をプロット linestyle='dashed', color='black', lw=0.5) ax.set_xticks([]) # x軸ラベルだけを消す ax.set_yticks([]) # y軸ラベルだけを消す # 決定係数R2が閾値以上だったらプロット背景を赤くする if corr[0, 1] ** 2 >= threshold: ax.set_facecolor('red') # グラフを表示する。 plt.show() plt.close() |
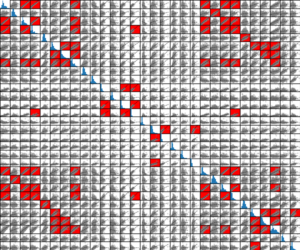
こちらも図を再掲します。
まとめ
本ページでは多変量データセットを効率よく相関分析できるように、ペアプロット(行列散布図)をカスタマイズする方法を紹介しました。
seabornを使わなくても、ペアプロットは散布図とヒストグラムで構成されているため、個々の計算は特に特別な知識がいるものではありませんでした(最も躓きやすい所はグラフを隙間なく詰める方法等のグラフィカルな部分かと思います)。
今回は相関係数や決定係数を使って可視化の方法を工夫してみましたが、ぱっと見でどの辺に相関の高い所があるかを分析できるようになったと思います。
重回帰分析等の多変量解析では多重共線性が問題でフィッティング精度が落ちることがよくあると思いますので、機械学習等でデータを入力する前によくデータを見るということを習慣付けたいですね。
データ分析はあらゆる処理において重要です!是非効率的な可視化を!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!