
機械学習ではサポートベクターマシン(SVM)が非常に優秀な分類性能を示しますが、SVMはサポートベクター回帰(SVR)として回帰問題にも適用が可能です。ここではSVRの概要とPython/scikit-learnによる実装までを紹介します。
こんにちは。wat(@watlablog)です。ここでは、非線形フィッティング問題を例としてサポートベクター回帰(SVR)の説明と実装の習得を目標とします!
サポートベクターマシン(SVM)による回帰とは?
SVMによる分類のおさらい
サポートベクターマシン(SVM:Support Vector Machine)とは、主に分類を行うための機械学習アルゴリズムとして考案されました。
初めは1963年にVladimir N. Vapnik, Alexey Ya. Chervonenkisらが線形の分類器として発表しましたが、1993年にBernhard E. Boser, Isabelle M. Guyon, Vladimir N. Vapnikらが非線形の分類へ拡張したことで一躍脚光を浴びた計算手法です。
当WATLABブログでは「Python機械学習初心者用!サポートベクターマシンの概要と実装」という記事でサポートベクターマシンによる線形、非線形分類の概要を説明していますが、カーネル関数を使う部分は感動ものでした。
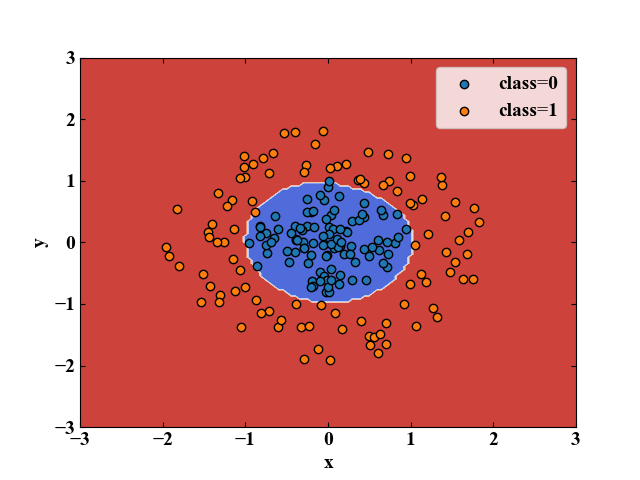
上記画像はSVMによる分類の例ですが、Pythonであればこのような非線形の分類もわずか数行のコードでできてしまいます。
しかし、SVMは回帰分析にも適用可能であり、分類を行うサポートベクターマシンをSVC(Support Vector Classification)と呼ぶのに対し、回帰を行うサポートベクターマシンをSVR(Support Vector Rigression)と呼びます。
回帰分析とは、「Python機械学習!scikit-learnによる単回帰分析」や「Python機械学習!scikit-learnによる重回帰分析」で紹介したように、あるデータ群にフィットするようなモデル(式)を構築することで、未知の値を予測する分析のことを意味します。
上記2つの記事はいずれも線形の回帰分析の内容ですが、ここで紹介するサポートベクター回帰(SVR)は非線形回帰も容易である強みがあります。
それでは早速SVRの概要を説明していきましょう!
SVRを理解するために必要な知識
サポートベクトルを使うのは同じ
SVRはSVCと同様にサポートベクトルを使います。分類問題の場合、サポートベクトルを用いると境界付近のデータ点のみを使って決定境界が引かれます(下図は前回の記事内の図を再掲)。
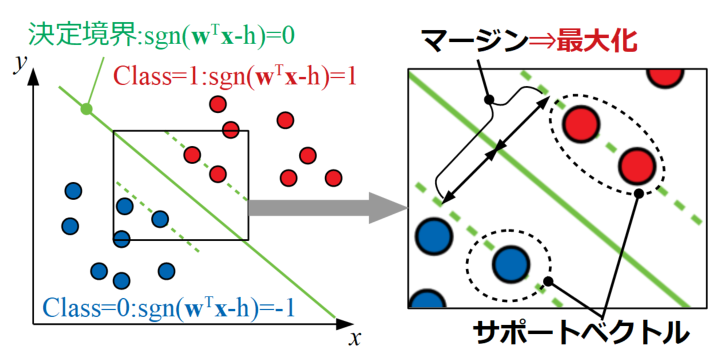
これは境界付近のデータ以外が加わっても決定境界が揺るがないことを意味するため、非常にロバスト性が高い(外乱による変化が少ないという意味)モデルと言うことが出来ます。
回帰問題では、データ点が少し追加されただけで回帰式(モデル)の形状が変わってしまったら非常に扱い難いため、サポートベクトルを使うSVRはロバスト性が高いという点でも人気があります。
\(\varepsilon\)-不感損失関数
SVCと異なる点として、SVRでは\(\varepsilon\)-不感損失関数を使用する点があります。
回帰問題では、予めそのデータ群を表現することが可能であると想定した関数\(f(x)\)を定義して、実際のデータ点\(y_{i}\)との誤差\(\varepsilon_{i}=y_{i}-f(x_{i})\)の合計を最小にする計算を行います。
これは「Pythonでカーブフィット!最小二乗法で直線近似する方法」で紹介した最小二乗法でも同じ考え(記事内式(1))であるため、誤差を定式化するための常套手段と言えますね!
SVRは回帰問題なので同じように誤差を計算しますが、誤差がある一定値\(\varepsilon\)を超えるまでは0と扱う\(\varepsilon\)-不感損失関数を使うと、\(-\varepsilon\)<誤差<\(\varepsilon\)の範囲のデータ点は誤差評価の対象となりません。
下図に\(\varepsilon\)-不感損失関数を示します。ちなみに、\(-\varepsilon\)<誤差<\(\varepsilon\)の範囲は\(\varepsilon\)チューブと呼ばれます。
そしてこの\(\varepsilon\)はエンジニアが事前に値を決めておく必要のあるハイパーパラメータとなります。
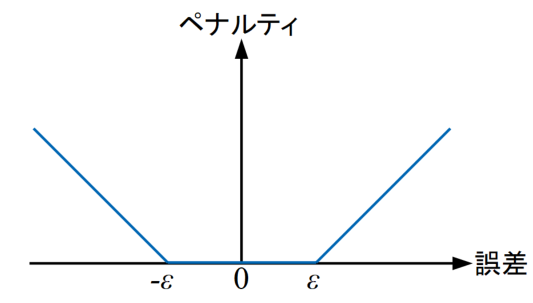
サポートベクターマシンでは重み係数ベクトルの最小化も行っているので、\(\varepsilon\)-不感損失関数を使って見積もった誤差関数の最小化を共に行うことによって過学習(オーバーフィッティング)を防ぎます。
分類問題で扱うSVCはサポートベクトルが決定境界近傍の点だったけど、回帰問題のSVRは±\(\varepsilon\)の範囲の外側をサポートベクトルとして扱うイメージかな?
ちょっと理解が及ばないので継続して学習してみます!
カーネル関数を使って非線形回帰が可能
SVCと同じように、非線形のカーネル関数(RBFカーネル、多項式カーネル、シグモイドカーネル等)を使うことで非線形の回帰分析を行うことも可能です。
この非線形回帰が容易という所がおそらく最もサポートベクター回帰が使われる理由であると考えられます。
カーネル関数の概要や非線形カーネル関数を使ったSVCの実装については「Python機械学習初心者用!サポートベクターマシンの概要と実装」の記事を参照してみて下さい。
Python/scikit-learnによるSVRコード
2D線形データセットで確認(\(y=ax+b\))
全コード
それでは実際にSVRをPythonを使って実装していきます。「実装」と言っても、車輪の再発明をするわけではなく、scikit-learnというライブラリを使って計算を行うだけです。
まずは最も簡単な直線の方程式をベースにしたデータセットでSVRの効果を見てみます。
以下に全コードを示しますが、SVRの時と全く同じ流れなので、詳細説明は要らないのではと思います。
データにはノイズを含ませ、サポートベクターマシンのsvm.SVRで回帰に関する学習をさせた後、テストデータを作成して予測値をプロットするという流れです。
直線の式を回帰分析するので、カーネル関数は線形カーネルを使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 |
import numpy as np from sklearn import svm from matplotlib import pyplot as plt # データを用意する------------------------------------------------------------------ a = 1.0 # 直線の傾き b = 0.5 # y切片 x = np.arange(1.0, 8.0, 0.2) # 横軸を作成 noise = np.random.normal(loc=0, scale=0.5, size=len(x)) # ガウシアンノイズを生成 y = a * x + b + noise # 学習用サンプル波形 # ---------------------------------------------------------------------------------- # サポートベクターマシンによる学習 model = svm.SVR(C=1.0, kernel='linear', epsilon=0.1) # 正則化パラメータ=1, 線形カーネルを使用 model.fit(x.reshape(-1, 1), y) # フィッティング # 学習済モデルを使って予測 x_reg = np.arange(0, 10, 1) # 回帰式のx軸を作成 y_reg = model.predict(x_reg.reshape(-1, 1)) # 予測 r2 = model.score(x.reshape(-1, 1), y) # 決定係数算出 # ここからグラフ描画--------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットの準備。 ax1.scatter(x, y, label='Dataset', lw=1, marker="o") ax1.plot(x_reg, y_reg, label='Regression curve', color='red') plt.legend() # グラフ内に決定係数を記入 plt.text(0.5, 7, '$\ R^{2}=$' + str(round(r2, 2)), fontsize=20) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------------------------------------- |
実行結果
下図が実行結果で得られるプロットです。グラフ内に決定係数\(R^{2}\)も書いてみました。
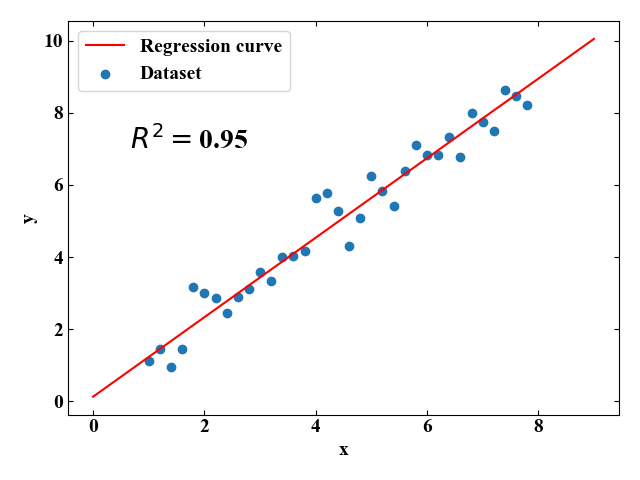
これは序の口!これが出来なきゃ使い物になりませんもんね!
2D非線形データセットで確認(\(y=\sin x\))
全コード
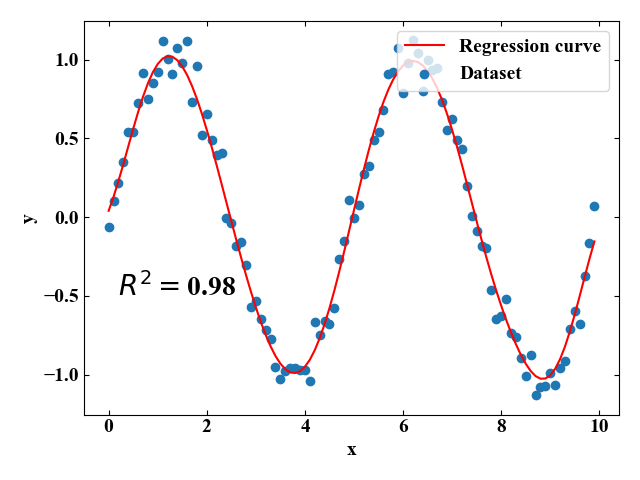
次は同じく2Dプロットですが、非線形の場合はどうなるか試してみます。ここで、サンプルとなる関数は\(y=\sin x\)です。
np.polyfitとかではなかなかフィッティングできない周期関数です。今回は非線形関数で回帰を行うため、カーネル関数はRBFカーネル(ガウシアンカーネル)を使いました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 |
import numpy as np from sklearn import svm from matplotlib import pyplot as plt # データを用意する------------------------------------------------------------------ x = np.arange(0.0, 10.0, 0.1) # 横軸を作成 noise = np.random.normal(loc=0, scale=0.1, size=len(x)) # ガウシアンノイズを生成 y = np.sin(2 * np.pi * 0.2 * x) + noise # 学習用サンプル波形 # ---------------------------------------------------------------------------------- # サポートベクターマシンによる学習 model = svm.SVR(C=1.0, kernel='rbf', epsilon=0.1, gamma='auto') # RBFカーネルを使用 model.fit(x.reshape(-1, 1), y) # フィッティング # 学習済モデルを使って予測 x_reg = np.arange(0, 10, 0.1) # 回帰式のx軸を作成 y_reg = model.predict(x_reg.reshape(-1, 1)) # 予測 r2 = model.score(x.reshape(-1, 1), y) # 決定係数算出 # ここからグラフ描画--------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットの準備。 ax1.scatter(x, y, label='Dataset', lw=1, marker="o") ax1.plot(x_reg, y_reg, label='Regression curve', color='red') plt.legend(loc='upper right') # グラフ内に決定係数を記入 plt.text(0.0, -0.5, '$\ R^{2}=$' + str(round(r2, 2)), fontsize=20) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------------------------------------- |
実行結果
実行結果はこちら。サイン波形でもよく回帰出来ています。
すごく簡単にできますが、まだまだ…これは想定内。
正弦波であれば誤差関数を設定して最小二乗法を適用してあげれば自分でも作れそうですもんね!
3Dデータセットで確認①(\(z = \sin x \cos y\))
全コード
今回は\(x\), \(y\)は完全にランダムな値にし、\(z\)として\(z = \sin x \cos y\)をベース関数とするデータセットに対し回帰を行います。ベース関数がわかっていれば、自力で回帰するのは無理ではないと思いますが、次元が増えるとかなりきつそう。
先ほどの2Dプロットと同様にRBFカーネルを使い、ハイパーパラメータの値も同じです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
import numpy as np from sklearn import svm from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # データを用意する------------------------------------------------------------------ x = np.random.uniform(0, 10, 500) # ノイズを含んだx軸を作成 y = np.random.uniform(0, 10, 500) # ノイズを含んだy軸を作成 z = np.sin(x) * np.cos(y) * np.random.uniform(1, 1.5, 500) # ノイズを含んだz値を作成 X = np.c_[x, y] # SVRが使えるように変数を結合 # --------------------------------------------------------------------------------- # サポートベクターマシンによる学習 model = svm.SVR(C=1.0, kernel='rbf', gamma='auto', epsilon=0.1) # RBFカーネルを使用 model.fit(X, z) # フィッティング # 学習済モデルを使って予測 grid_line = np.arange(0, 10, 0.5) # 回帰式の軸を作成 X2, Y2 = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z2 = model.predict(np.array([X2.ravel(), Y2.ravel()]).T) # 予測 Z2 = Z2.reshape(X2.shape) # プロット用にデータshapeを変換 r2 = model.score(X, z) # 決定係数算出 # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') # データプロットする。 ax1.scatter3D(x, y, z, label='Dataset') ax1.plot_wireframe(X2, Y2, Z2, label='Regression plane K=rbf') plt.legend() # グラフ内に決定係数を記入 ax1.text(0.0, 0.0, 1.5, zdir=(1,1,0), s='$\ R^{2}=$' + str(round(r2, 2)), fontsize=20) # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------------------------------------- |
実行結果
先ほどのサイン波の回帰とハイパーパラメータは同じなのに\(R^{2}\)が0.99とかなり高い回帰モデルが出来上がりました。
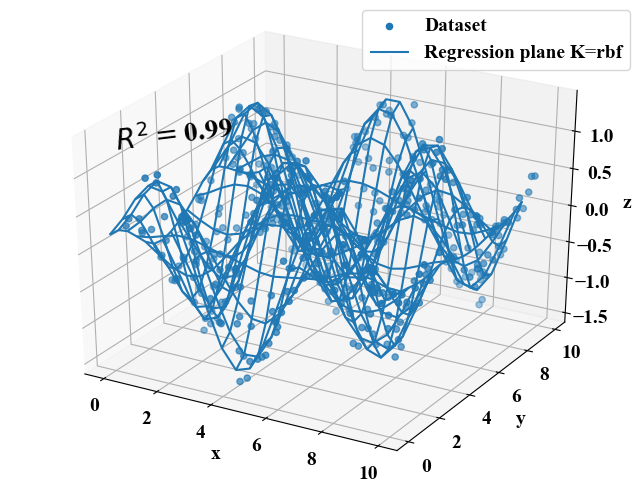
これは驚きました!思わずプログラムのバグ(回帰曲面が元のデータをメッシュにしただけになっているのでは?)を疑ってしまうほど!でもバグはなく、こんなに凹凸のある非線形関数もRBFカーネルで回帰出来ているという事実がわかりまし!
3Dデータセットで確認②(\(z = x^{2} y^{2}+xy\))
全コード
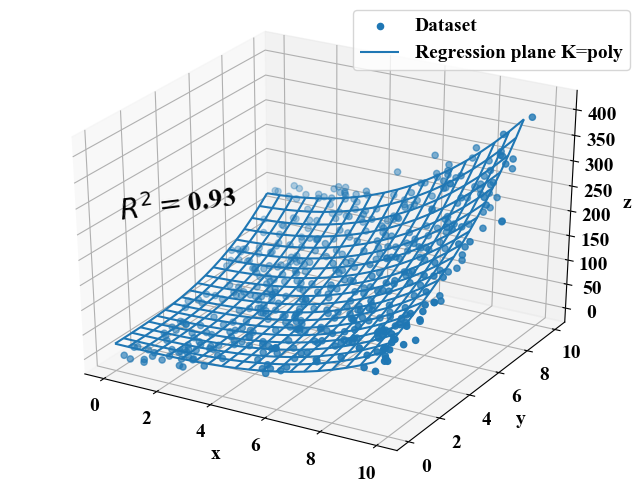
次は\(z = x^{2} y^{2}+xy\)という関数をベース関数にしたサンプルです。結論から述べると、この関数はRBFカーネルではうまくいかなかったので多項式カーネル(kernel='poly')を使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 |
import numpy as np from sklearn import svm from matplotlib import pyplot as plt from mpl_toolkits.mplot3d import Axes3D # データを用意する------------------------------------------------------------------ x = np.random.uniform(0, 10, 500) # ノイズを含んだx軸を作成 y = np.random.uniform(0, 10, 500) # ノイズを含んだy軸を作成 z = (x ** 2 + y ** 2 + x * y) * np.random.uniform(1, 1.5, 500) # ノイズを含んだz値を作成 X = np.c_[x, y] # SVRが使えるように変数を結合 # --------------------------------------------------------------------------------- # サポートベクターマシンによる学習 model = svm.SVR(C=1.0, kernel='poly', gamma='auto', epsilon=0.1) # 多項式カーネルを使用 model.fit(X, z) # フィッティング # 学習済モデルを使って予測 grid_line = np.arange(0, 10, 0.5) # 回帰式の軸を作成 X2, Y2 = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z2 = model.predict(np.array([X2.ravel(), Y2.ravel()]).T) # 予測 Z2 = Z2.reshape(X2.shape) # プロット用にデータshapeを変換 r2 = model.score(X, z) # 決定係数算出 # ここからグラフ描画---------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = Axes3D(fig) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax1.set_zlabel('z') # データプロットする。 ax1.scatter3D(x, y, z, label='Dataset') ax1.plot_wireframe(X2, Y2, Z2, label='Regression plane K=poly') plt.legend() # グラフ内に決定係数を記入 ax1.text(0.0, 0.0, 300, zdir=(1,1,0), s='$\ R^{2}=$' + str(round(r2, 2)), fontsize=20) # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------------------------------------- |
実行結果
結果はこちら。この関数も\(R^{2}\)が0.93と高く、問題無く回帰モデルが出来ていると言うことが出来そうです。
SVRが上手く働かなかった例(カーネル関数の選定はかなり大事)
先ほどまでの3D回帰分析の2例ではうまくフィッティングが出来ていましたが、以下のようにカーネル関数を入れ替えてしまうと途端に決定係数\(R^{2}\)が下がってしまいます。
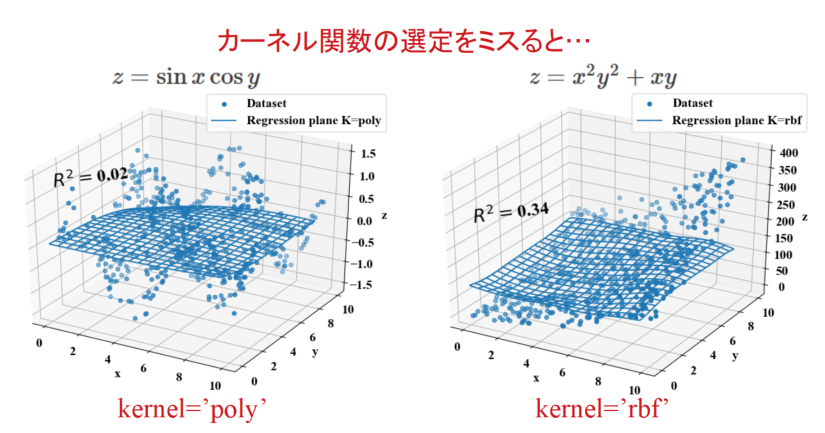
そもそもフィッティングに適していない関数を選んでしまうと、ハイパーパラメータの調整程度では精度を出すことは出来ないということですね。3Dまでなら視覚的にわかりやすいけど、多数の特徴量からなる超平面だと中々ハマりそうなので注意!
決定係数\(R^{2}\)(.score)を毎回確認するのが良いみたいです。
まとめ
本記事ではサポートベクターマシンで通常行う分類問題SVCのおさらいと、回帰問題SVRへ適用する時の変化点等の概要を学習しました。
とはいえ、データ分析として使ってアウトプットを得るだけであれば、SVCとSVRはほぼ同じコードで可能であることがわかりました。
この記事ではカーネル関数やハイパーパラメータの調整はまだ手動で行っている程度ですので、別途サーチアルゴリズムの調査を経てようやく使いこなせるようになると考えられます。
これで分類と回帰のサポートベクターマシンを使えるようになりました!一通りできることをなぞってみて、その後にグリッドサーチや前処理を詰めて行きたいと思います!Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント