Pythonでケプストラム分析!音声から声帯情報を取得してみた

ケプストラム分析を行うと、音声から声帯振動スペクトルと声道スペクトルを分離することが出来ます。これらの情報は声帯の情報であるため、機械学習にも使われることがあります。ここでは、Pythonを使ってケプストラム分析をする方法を紹介します。

こんにちは。wat(@watlablog)です。
今回は音声信号処理でよく知られるケプストラム分析をPythonでやってみました！

※注意：今回の記事は音響学の専門家でない筆者が学習した結果であり、自分が理解したと思っている内容を記載しています。そのため厳密に工学的に正確な説明になっているわけではないと思いますので、ここに記載の内容を引用する場合は十分ご注意下さい！

目次（項目クリックでジャンプできます）

ケプストラム分析で声帯情報を取得することが出来る

ケプストラムとは？

ケプストラム（Cepstrum）は、スペクトラム（Spectrum）の最初の4文字を逆にしたアナグラムになっています。

スペクトラムはある時間信号 $x (t)$ をフーリエ変換して得られる周波数領域の関数 $x (f)$ のことですが、周波数領域のスペクトルを時間信号とみなし、さらにフーリエ変換を施したものをケプストラムと呼びます。このことから、スペクトルのスペクトルとも呼ばれています。

スペクトルに現れる細かい変動と緩やかな変動にはそれぞれ特徴的な意味を持つ場合が多く、特に人の音声信号処理をする場合には「声帯振動スペクトル」と「声道スペクトル」という重要な要素があります。

ケプストラム分析をすることで、スペクトルからそれらの特徴を分離することが出来ます。

wikiによると、地震の振動や爆弾の爆発を分析するためにも使われるとのことですが、このページでは僕（人）の声をサンプルに計算を試してみたいと思います。

声帯振動スペクトルと声道スペクトルとは？

「ケプストラム分析を使って声帯振動スペクトルと声道スペクトルを分離する」というのは、言葉ではわかりにくいと思いましたので図を作成してみました。

以下が人の音声からケプストラム分析を使って声帯振動スペクトルと声道スペクトルを抽出するイメージ図です。

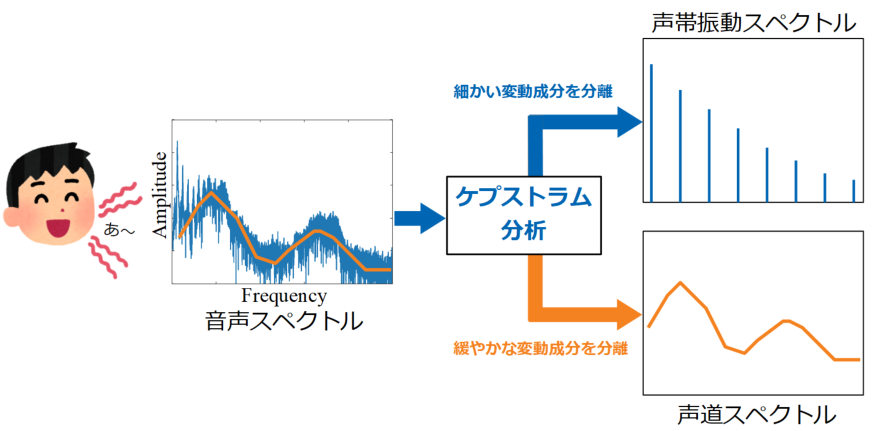
人の声帯が振動すると、基本波と基本波の等倍に発生する高調波が発生します。この声帯振動を周波数波形にしたものを声帯振動スペクトルと呼びます。

それだけであれば、基本波が最も振幅が高く高調波は次第に下がっていくスペクトルを示すはずですが、人は声道と呼ばれる管が音響特性を持っているためにスペクトル全体に緩やかな変動成分が乗ってきます。この緩やかな変動成分を声道スペクトルと呼びます。

ケプストラム分析をすることで、この声帯起因の細かい振動と、声道が持つ音響特性を示す成分を分離することが可能です。

音響特性というのは、高校物理の範囲でやっているような気柱の振動が原因の特性ですね。音が管の中で反射を繰り返すと、粒子速度と音圧といった物理量が定在波によって分布を持つようになります。

ケプストラム分析とは具体的にどんな計算をしている？

Pythonコードを眺める前に、具体的な計算フローを把握しておきましょう。

以下の図が今回行う計算のフローです。

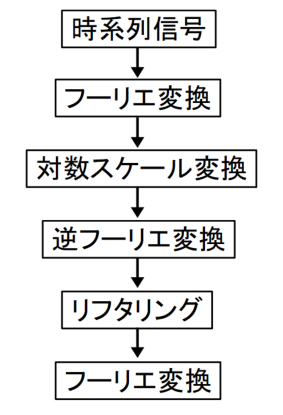
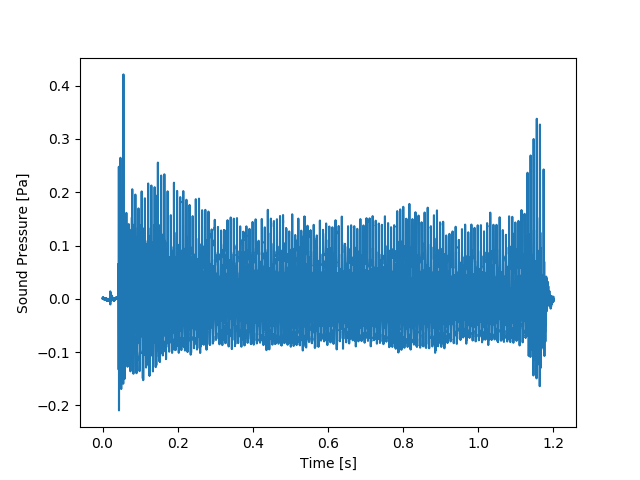
時系列信号は正弦波の合成で作成しても良いのですが、せっかくなので今回は実際の人の声を録音した音声ファイルとしてwavファイルを用意しました。

今回使用するwavファイルは筆者である僕の「あ～」という声です。wavファイルの取り扱いは「PythonのPySoundFileでwavファイル波形表示」や「Pythonでモノラルとステレオのwavファイルを保存する方法」を参照下さい。

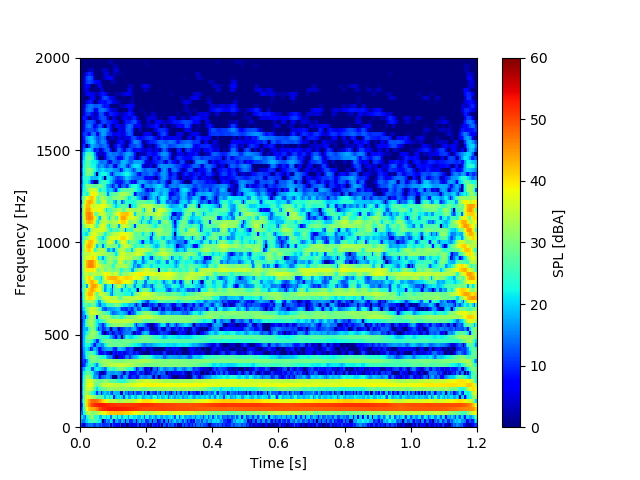
この音声信号をスペクトログラムとして、時間×周波数×振幅レベルを見てみますと、以下の図になります。スペクトログラム計算については「Pythonで音のSTFT計算を自作！スペクトログラム表示する方法」に詳細を記載しましたので、そちらの記事を参照下さい。

Pythonでケプストラム分析をするコード

全コード

それではいよいよPythonでケプストラム分析をするコードを紹介します。

以下が全コードです。詳細は後述します。グラフ設定部分が毎度のことながら長いですが、ケプストラム分析部分はそれほど長くありません。

import soundfile as sf
import numpy as np
from scipy import fftpack
from matplotlib import pyplot as plt

# リニア値をdB変換
def db(x, dBref):
    y = 20 * np.log10(x / dBref)                      # リニア値をdB値に変換
    return y                                          # dB値を返す

# dB値をリニア変換
def lin(x, dBref):
    y = dBref * 10 ** (x / 20)                        # dB値をリニア値に変換
    return y                                          # リニア値を返す

# フーリエ変換の振幅を正規化
def norm(spectrum, dBref):
    spectrum = lin(spectrum, dBref)                   # 計算のために一度リニア値に戻す
    spectrum = np.abs(spectrum / (len(spectrum) / 2)) # 正規化
    spectrum = db(spectrum, dBref)                    # dB値に戻す
    return spectrum

# wavの読み込み
path = 'a.wav'                                        # ファイルパスを指定
data, samplerate = sf.read(path)                      # wavファイルを開き、波形とサンプリングレートを取得

# ケプストラム分析
spec = fftpack.fft(data)                              # 時間波形をフーリエ変換してスペクトルにする
spec_db = db(spec, 2e-5)                              # スペクトルを対数(dB)にする(0dB=20[μPa])
ceps_db = np.real(fftpack.ifft(spec_db))              # 対数スペクトルを逆フーリエ変換してケプストラム波形を作る
index = 50                                            # ローパスリフターのカットオフ指標
ceps_db[index:len(ceps_db) - index] = 0               # ケプストラム波形の高次を0にする（ローパスリフター）
ceps_db_low = fftpack.fft(ceps_db)                    # ケプストラム波形を再度フーリエ変換してスペクトル包絡を得る

# グラフ用の軸を作成
frequency = np.linspace(0, samplerate, len(data))     # frequency軸を作成
quefrency = np.arange(0, len(data)) / samplerate      # quefrency軸を作成

# グラフ用に振幅を正規化
spec_db_amp = norm(spec_db, 2e-5)                     # 音声スペクトルの振幅成分を計算
ceps_db_low_amp = norm(ceps_db_low, 2e-5)             # ローパスリフター後のスペクトル包絡の振幅成分を計算

# ここからグラフ描画
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。
fig = plt.figure()
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('Frequency [Hz]')
ax1.set_ylabel('SPL [dB]')

# データプロット。
ax1.plot(frequency, spec_db_amp)
ax1.plot(frequency, ceps_db_low_amp, lw='4')

# スケールの設定をする。
ax1.set_xticks(np.arange(0, 20000, 1000))
ax1.set_xlim(0, 5000)
ax1.set_yticks(np.arange(-200, 200, 20))
ax1.set_ylim(-20, 80)

# レイアウト設定
fig.tight_layout()

# グラフを表示する。
plt.show()
plt.close()

import soundfile as sf

import numpy as np

from scipy import fftpack

from matplotlib import pyplot as plt

# リニア値をdB変換

def db(x, dBref):

y = 20 * np.log10(x / dBref) # リニア値をdB値に変換

return y # dB値を返す

# dB値をリニア変換

def lin(x, dBref):

y = dBref * 10 ** (x / 20) # dB値をリニア値に変換

return y # リニア値を返す

# フーリエ変換の振幅を正規化

def norm(spectrum, dBref):

spectrum = lin(spectrum, dBref) # 計算のために一度リニア値に戻す

spectrum = np.abs(spectrum / (len(spectrum) / 2)) # 正規化

spectrum = db(spectrum, dBref) # dB値に戻す

return spectrum

# wavの読み込み

path = 'a.wav' # ファイルパスを指定

data, samplerate = sf.read(path) # wavファイルを開き、波形とサンプリングレートを取得

# ケプストラム分析

spec = fftpack.fft(data) # 時間波形をフーリエ変換してスペクトルにする

spec_db = db(spec, 2e-5) # スペクトルを対数(dB)にする(0dB=20[μPa])

ceps_db = np.real(fftpack.ifft(spec_db)) # 対数スペクトルを逆フーリエ変換してケプストラム波形を作る

index = 50 # ローパスリフターのカットオフ指標

ceps_db[index:len(ceps_db) - index] = 0 # ケプストラム波形の高次を0にする（ローパスリフター）

ceps_db_low = fftpack.fft(ceps_db) # ケプストラム波形を再度フーリエ変換してスペクトル包絡を得る

# グラフ用の軸を作成

frequency = np.linspace(0, samplerate, len(data)) # frequency軸を作成

quefrency = np.arange(0, len(data)) / samplerate # quefrency軸を作成

# グラフ用に振幅を正規化

spec_db_amp = norm(spec_db, 2e-5) # 音声スペクトルの振幅成分を計算

ceps_db_low_amp = norm(ceps_db_low, 2e-5) # ローパスリフター後のスペクトル包絡の振幅成分を計算

# ここからグラフ描画

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure()

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Frequency [Hz]')

ax1.set_ylabel('SPL [dB]')

# データプロット。

ax1.plot(frequency, spec_db_amp)

ax1.plot(frequency, ceps_db_low_amp, lw='4')

# スケールの設定をする。

ax1.set_xticks(np.arange(0, 20000, 1000))

ax1.set_xlim(0, 5000)

ax1.set_yticks(np.arange(-200, 200, 20))

ax1.set_ylim(-20, 80)

# レイアウト設定

fig.tight_layout()

# グラフを表示する。

plt.show()

plt.close()

ケプストラム分析のコード解説

時系列信号をフーリエ変換して対数スケールにする

ケプストラム分析には時間信号をフーリエ変換した音声スペクトルを使いますが、縦軸の値を対数スケールにする必要があります。

対数スケールにするということは、dB変換することと同じ意味です。せっかく音声を扱うのでただlogにするだけでなく、「0dB=20μPa」という国際規格に則ったdB変換を行いました。

dBについての詳細は「Pythonで音圧のデシベル(dB)変換式と逆変換式！」をご確認下さい。

以下のコードは、上記記事に載っているdB変換式を使ってフーリエ変換後のスペクトルを対数スケールにしている部分です。

# リニア値をdB変換
def db(x, dBref):
    y = 20 * np.log10(x / dBref)                      # リニア値をdB値に変換
    return y                                          # dB値を返す

spec = fftpack.fft(data)                              # 時間波形をフーリエ変換してスペクトルにする
spec_db = db(spec, 2e-5)                              # スペクトルを対数(dB)にする(0dB=20[μPa])

# リニア値をdB変換

def db(x, dBref):

y = 20 * np.log10(x / dBref) # リニア値をdB値に変換

return y # dB値を返す

spec = fftpack.fft(data) # 時間波形をフーリエ変換してスペクトルにする

spec_db = db(spec, 2e-5) # スペクトルを対数(dB)にする(0dB=20[μPa])

dB変換する前の音声スペクトルが以下の図になるのに対して、

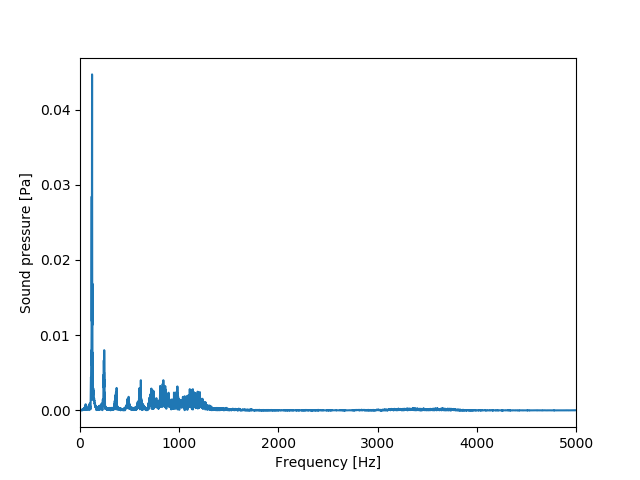
dB変換して対数スケールにすることで以下の図のようにリニア値では細かい変化も大きく視認することができるようになります。

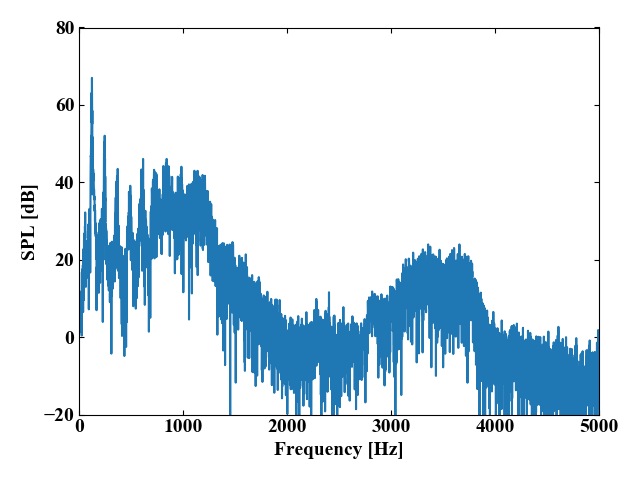
対数スペクトルを逆フーリエ変換してケプストラム波形を作る

ここからが本題のケプストラム分析になります。

といっても、先ほどの対数スペクトルを逆フーリエ変換して実部をとるだけです。コードは以下の部分です。

ceps_db = np.real(fftpack.ifft(spec_db))              # 対数スペクトルを逆フーリエ変換してケプストラム波形を作る

1	ceps_db = np.real(fftpack.ifft(spec_db)) # 対数スペクトルを逆フーリエ変換してケプストラム波形を作る

このceps_dbこそがケプストラム波形です。横軸は[Hz]を逆フーリエ変換しているので[s]になりますが、名称はQuefrency(ケフレンシ)です。波形の最初の方に大きな変動成分があります。

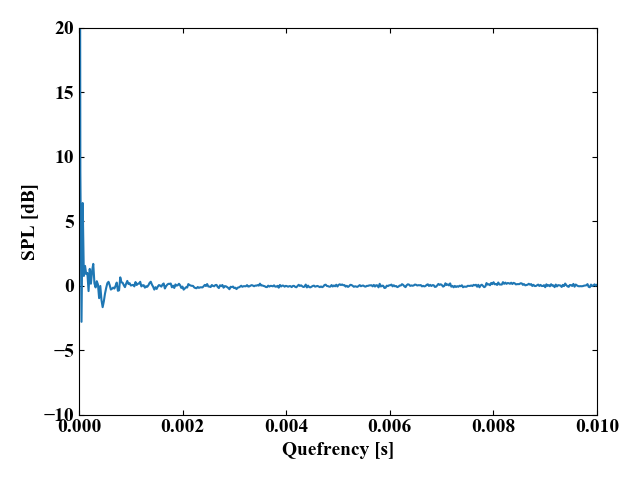
この波形は拡大図ですが、全体を見るとFFTした時に鏡像があるように波形の最後の方にも大きな変動成分があります。

ローパスリフタをかける

リフタ(Lifter)というのは、フィルタ(Filter)の最初の3文字をひっくり返したアナグラムです。文字通り、フィルタの役割をしています。

先ほどのケプストラム波形の低次成分がスペクトル波形の緩やかな変動成分を表しているので、高次成分を0にすればローパスをかけた意味になります。

以下がローパスリフタのコードですが、波形を1D配列と見た時に0を置換しているだけです。但し、ケプストラム波形は横軸の半分の位置で折り返されているため、index=50として低次成分を50個残して他を0にしたい時は、最後から50個も残す必要があります。

index = 50                                            # ローパスリフターのカットオフ指標
ceps_db[index:len(ceps_db) - index] = 0               # ケプストラム波形の高次を0にする（ローパスリフター）

1 2	index = 50 # ローパスリフターのカットオフ指標 ceps_db[index:len(ceps_db) - index] = 0 # ケプストラム波形の高次を0にする（ローパスリフター）

ローパスリフタをかけると以下の波形になります。

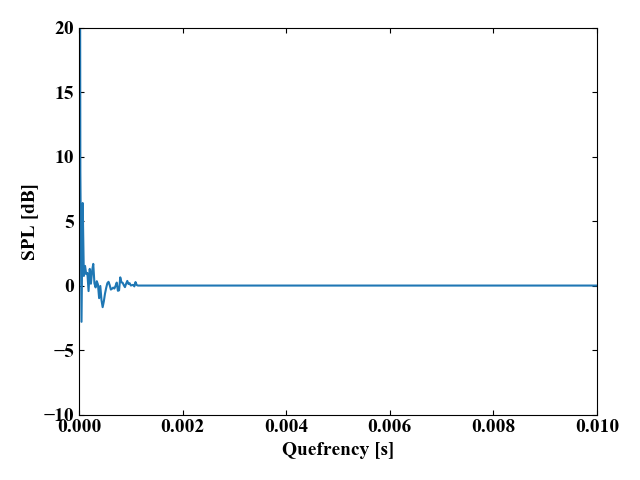
再度フーリエ変換してスペクトル包絡を得る

最後はローパスリフタ後のケプストラム波形を再度フーリエ変換することで音声スペクトルの内で緩やかな変動成分である「声道スペクトル」を得ることができます。人によってはスペクトル包絡と呼ぶ人もいるようですね。

ceps_db_low = fftpack.fft(ceps_db)                    # ケプストラム波形を再度フーリエ変換してスペクトル包絡を得る

1	ceps_db_low = fftpack.fft(ceps_db) # ケプストラム波形を再度フーリエ変換してスペクトル包絡を得る

全コードで紹介している内容は元のスペクトルとスペクトル包絡を重ねており、以下の結果を得ることができます。

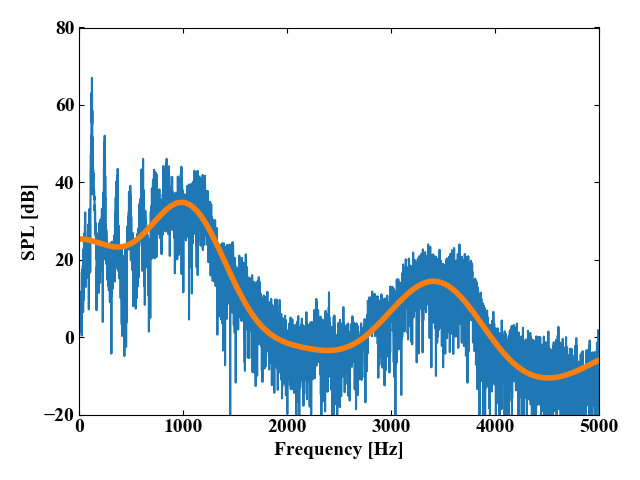
見事元のスペクトル波形の緩やかな成分を得ることができました！

全コードの中では振幅成分の正規化と称した計算を行っていますが、これは振幅成分の高さの辻褄を合わせるために行っています。やり方は色々あるようですが、詳しくは「PythonでFFT！SciPyのFFTまとめ」に記載しましたので、気になる方は見てみて下さい（正式なやり方があったら教えて頂きたい…）。

まとめ

本記事ではケプストラム分析の概要を説明し、声帯振動スペクトルと声道スペクトルを紹介しました。

試しに僕の声でスペクトルを見てみた所、確かに等倍次数で発生する振動成分と周波数軸で確認できる緩やかな変動成分があることがわかりました。

このページではケプストラム分析のフローも併せて紹介し、Pythonでコーディングしてスペクトル包絡を抽出できることを確かめました。

ケプストラム分析という音声処理っぽいことができてきました！Cepstrum, Quefrency, Lifter…工学の世界もシャレたネーミングをするんですね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

ケプストラム分析で声帯情報を取得することが出来る

ケプストラムとは？

声帯振動スペクトルと声道スペクトルとは？

ケプストラム分析とは具体的にどんな計算をしている？

Pythonでケプストラム分析をするコード

全コード

ケプストラム分析のコード解説

時系列信号をフーリエ変換して対数スケールにする

対数スペクトルを逆フーリエ変換してケプストラム波形を作る

ローパスリフタをかける

再度フーリエ変換してスペクトル包絡を得る

まとめ

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

ケプストラム分析で声帯情報を取得することが出来る

ケプストラムとは？

声帯振動スペクトルと声道スペクトルとは？

ケプストラム分析とは具体的にどんな計算をしている？

Pythonでケプストラム分析をするコード

全コード

ケプストラム分析のコード解説

時系列信号をフーリエ変換して対数スケールにする

対数スペクトルを逆フーリエ変換してケプストラム波形を作る

ローパスリフタをかける

再度フーリエ変換してスペクトル包絡を得る

まとめ

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル