前回は最小二乗法を使って直線近似する方法を習得しました。最小二乗法は何も直線を近似させるためだけにあるわけではありません。ここでは、同様の考え方で2次以降の高次関数へのフィッティングがPythonで簡単にできることを示します。
こんにちは。wat(@watlablog)です。
最小二乗法は習得すると色々なデータ分析が捗ります！ここでは2次以降の場合の最小二乗近似、多項式カーブフィットについて紹介します！
最小二乗法を高次へ拡張する時の考え方
1次近似（直線近似）のおさらい
「Pythonでカーブフィット！最小二乗法で直線近似する方法」では主に最小二乗法の概要や、式展開による公式の導出を行い、あるばらつきを持ったデータを直線近似する方法を紹介しました。
グラフで図示すると、以下のようになります。
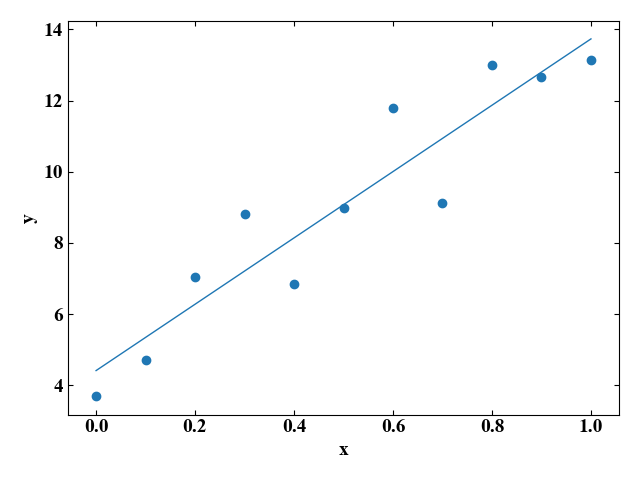
これはあるばらつきを持ったデータを、1次関数と仮定して\(y=ax+b\)の直線と各データポイントの誤差が最も小さくなるように近似パラメータ\(a\)と\(b\)を決めた結果です。
先ほど紹介した記事では、まず誤差を数式で表現し、さらに誤差を二乗しました。
そして各パラメータで独立に微分し、連立偏微分方程式を解くことで回帰直線のパラメータ値を決定していきました。
2次以降の高次関数も同様に最小二乗法を適用可能です。
そして基本的な流れは全て同じなので、以下考え方を紹介したいと思います。
最小二乗法の一般的な考え方
データの要素に名前を付ける
2次関数、3次関数と高次の関数になっても、まずは関数と誤差を数式で表現する必要があります。
直線の時は\(y=ax+b\)と置いていましたが、今回は一般的な関数として\(f(x)\)と置いています。
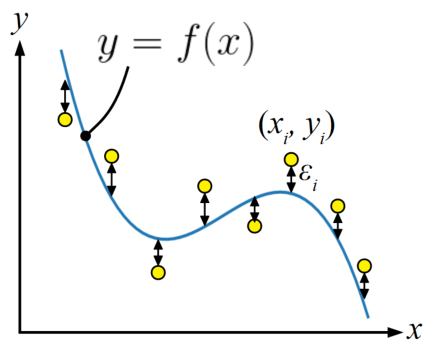
ここで、上記グラフ内の黄色いデータポイントと関数\(f(x)\)の誤差\(
\varepsilon\)は以下の式(1)で表現することができます。
$$\varepsilon = y_{i} - f(x_{i}) (1)$$
誤差を二乗する
最小二乗法の極意は式(1)で表現した誤差\(\varepsilon\)を式(2)と二乗することにあります。
$$\varepsilon^{2} = \left \{ y_{i} - f(x_{i}) \right \}^{2} (2)$$
誤差を二乗することで、負の値が無くなるという効果を狙っています。
近似パラメータで偏微分する
誤差を数式で表現できたので、次はその誤差を最小化します。
最小化に使用するパラメータは関数\(f(x)\)を構成するものを全てとります。
例えば1次近似であれば\(y=ax+b\)がフィッティングに使用する関数なので、\(a\)と\(b\)が関数を構成するパラメータとなります。
一般化のためにはこの\(a\)と\(b\)を\(a_{1}\)と\(a_{2}\)としましょう。
では2次関数はどうでしょうか？
2次関数の一般式は先ほどの例に習って表現すると\(y=a_{1}x^2+a_{2}x+a_{3}\)です。
このように、次数が増えれば増えるほど式を説明する係数\(a\)は数を増やしていきます。
この係数を\(a_{k}\)（\(k=1, 2, …n)\)と表現することができます。
この係数\(a_{k}\)のそれぞれについて誤差の二乗の総和\(S\)をとり、その微分形を式(3)と表現し、=0と置きます。
$$\frac{\partial S}{\partial a_{k}}=0 (3)$$
各パラメータ\(a_{k}\)において、それぞれ傾きが0になる（微分した結果が0）結果を求めれば良いので、この式は高次になればなるほど式の数が増える連立偏微分方程式を解くということになります。
次数が増えたら式構築が面倒で、さらに連立方程式を解かなけらばいけない！大変（？）だ！！
しかし、Pythonなら何次でも簡単に\(a_{k}\)を求めるpolyfit関数がありますので、以下に紹介します！
Pythonによる多項式近似コード!様々な関数への適用例
2次関数
1次関数は「Pythonでカーブフィット！最小二乗法で直線近似する方法」で紹介しましたので、まずは2次関数へ近似させるコードを以下に示します。
np.polyfitの引数に2を指定することが2次関数へ近似させる意味を持ちます。
2次関数に近似させると、近似パラメータは3個出力されるので、coe（coefficientの略）から取り出してy_fitを作っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np from matplotlib import pyplot as plt # ばらつきを持った2次関数の波形を生成 a1 = 1 a2 = 1 a3 = 1 x = np.arange(-5, 5, 0.2) # 時間軸配列を作成 noise = np.random.normal(loc=0, scale=2, size=len(x)) # ガウシアンノイズを生成 y = a1 * x ** 2 + a2 * x + a3 + noise # 2次関数にノイズを重畳 # 近似パラメータakを算出 coe = np.polyfit(x, y, 2) print(coe) # 得られたパラメータakからカーブフィット後の波形を作成 y_fit = coe[0] * x ** 2 + coe[1] * x + coe[2] |
上記コードは、実験風なばらつきを持った波形生成にガウシアンノイズを使っています。ガウシアンノイズについての詳細は「Pythonでガウス分布を持つノイズの作り方と調整方法」を参照下さい。
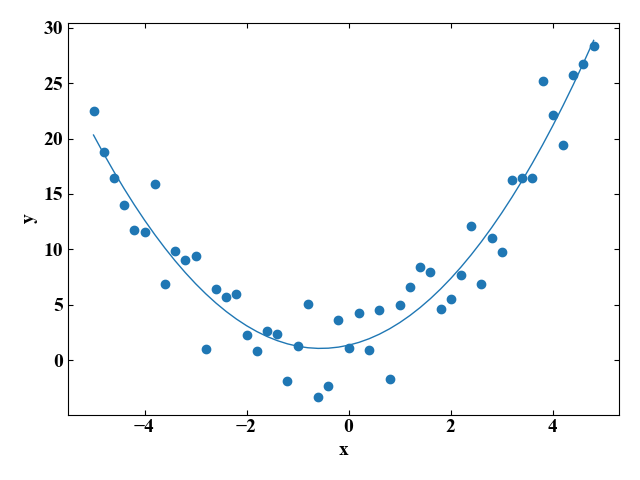
コード内のyとy_fitをグラフ表示させると以下の図になります。
良い感じにフィットした曲線になっていますね。
3次関数
3次関数の場合も同様です。以下にコードを示しますが、近似に関する部分はnp.polyfitの引数に3を指定している所と、カーブフィット波形生成部分の項が増えている所が先ほどとの違いになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 |
import numpy as np from matplotlib import pyplot as plt # ばらつきを持った3次関数の波形を生成 a1 = -2 a2 = 1 a3 = 20 a4 = 1 x = np.arange(-5, 5, 0.2) # 時間軸配列を作成 noise = np.random.normal(loc=0, scale=10, size=len(x)) # ガウシアンノイズを生成 y = a1 * x ** 3 + a2 * x ** 2 + a3 * x + a4 + noise # 3次関数にノイズを重畳 # 近似パラメータakを算出 coe = np.polyfit(x, y, 3) print(coe) # 得られたパラメータakからカーブフィット後の波形を作成 y_fit = coe[0] * x ** 3 + coe[1] * x ** 2 + coe[2] * x + coe[3] |
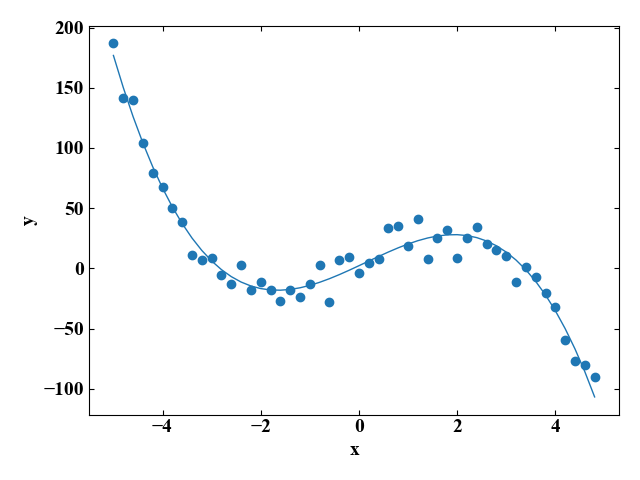
このコードを実行し、yとy_fitをグラフ表示すると以下の図が得られます。
こちらも見事にカーブフィットできていますね。
おまけ1：相関係数\(R\)と決定係数\(R^{2}\)
以下のnp.corrcoef()を使う事で相関係数\(R\)を算出する事が出来ます。また、相関係数を二乗する事で関数がどれだけフィットしているかを示す決定係数\(R^{2}\)を計算する事が出来ます。
|
1 2 3 4 |
# 相関係数と決定係数を計算する r = np.corrcoef(y, y_fit)[0,1] # 相関係数R r2 = r ** 2 # 決定係数R^2 print(r, r2) |
Excelとはで近似曲線を書いた時にオプションで付ける事ができるアレですね。是非使ってみて下さい。
おまけ2：グラフ表示コード
最後にグラフ表示まで全て含めたコードを以下に紹介します。
このコードを丸ごとコピペして実行すると、上のグラフと同様の結果が得られますので、是非お持ちの環境で実行してみて下さい！
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 |
import numpy as np from matplotlib import pyplot as plt # ばらつきを持った3次関数の波形を生成 a1 = -2 a2 = 1 a3 = 20 a4 = 1 x = np.arange(-5, 5, 0.2) # 時間軸配列を作成 noise = np.random.normal(loc=0, scale=10, size=len(x)) # ガウシアンノイズを生成 y = a1 * x ** 3 + a2 * x ** 2 + a3 * x + a4 + noise # 3次関数にノイズを重畳 # 近似パラメータakを算出 coe = np.polyfit(x, y, 3) print(coe) # 得られたパラメータakからカーブフィット後の波形を作成 y_fit = coe[0] * x ** 3 + coe[1] * x ** 2 + coe[2] * x + coe[3] # 相関係数と決定係数を計算する r = np.corrcoef(y, y_fit)[0,1] # 相関係数R r2 = r ** 2 # 決定係数R^2 print(r, r2) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # データプロットの準備。 ax1.scatter(x, y, label='sample', lw=1, marker="o") ax1.plot(x, y_fit, label='fitted curve', lw=1) # グラフを表示する。 fig.tight_layout() plt.show() plt.close() |
まとめ
本記事では直線以外の最小二乗法によるカーブフィット方法の考え方とコード例を紹介しました。
np.polyfitはPython初心者にも使いやすく、簡単に多項式の近似パラメータを計算してくれることがわかりました。
最小二乗法によるカーブフィットはこれを使っておけば間違いないね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント