Pythonによる1自由度振動系の自由振動と強制振動を学んだので、モデルの周波数応答をみてみます。この記事は真面目に定常の周波数応答を行っているのではなく、運動方程式の過渡応答結果を単純に周波数軸で並べる方法を紹介します。
こんにちは。wat(@watlablog)です。
1自由度の振動は振動学の理論を理解するために非常に重要です。ではいったい1自由度の周波数応答はどうなっているのか？ちょっと自力でやってみました！
モデルの周波数応答を見る方法
直接法とモード法・過渡応答とは？
周波数応答解析とは、振動系の運動方程式を加振させて各周波数毎に振幅レベルがどうなるかを調べる時に利用されます。
そして解析の方法にはいくつか選択肢があります。
通常、周波数応答解析は定常な正弦波が入力された時の方程式を立て、ある周波数毎にその式を解いていくという手段をとります。
定常状態で立てた運動方程式をそのまま解く直接法、一度固有値解析をした後に、固有ベクトルを使ってモード座標に変換してから解くモード法等があり、一般に計算の効率化からモード法が広く使われています。
これらはいずれこのブログでも扱いたい所ですが…
しかし僕は直接法やモード法の存在は知っているけどまだ勉強不足でよくわかっていません！
…ということで、今回は運動方程式を何も手を加えずにごりごり解く過渡応答解析に挑戦します。
過渡応答解析とは、別名で時刻歴応答解析とも呼ばれ、「Pythonで1自由度減衰系の強制振動シミュレーション」でやっていた方法に他なりません。
今回はPythonのodeintによる数値解析を行った後、周波数軸で整理する方法を紹介します。
今回対象とする運動方程式
今回対象とするモデルは理解しやすい1自由度振動系モデルです。
このモデルは質量\(m\)を持った質点とばね定数\(k\)のばね、減衰係数\(c\)のダンパーで構成され、質点に強制的に周期外力\(F\)が働くモデルです。
運動方程式と外力は以下の式で与えます。外力\(F\)は周波数\(f\)の正弦波です。
$$m\ddot{x}+c\dot{x}+kx=F$$
$$F=A\sin (2\pi ft)$$
Pythonによる周波数過渡応答解析
全コード
上記モデル、運動方程式を解くコードを以下に示しますが、具体的な式変形や関数の使い方は「Pythonで1自由度減衰系の強制振動シミュレーション」に記載していますので、そちらをご覧下さい。
以下のコードで周波数応答解析をしている所は、「f=」で解析する周波数リストを作り、forループで各周波数におけるodeint計算をしている部分です。
odeintで得られた結果は時刻歴応答の結果ですが、rmsと実効値を算出し、周波数軸で並べています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 |
import numpy as np from scipy.integrate import odeint import matplotlib.pyplot as plt # mkc force system def func(state, t, m, k, c, A, f): x1, x2 = state dx2dt = - (c / m) * x2 - (k / m) * x1 + A * np.cos(2 * np.pi * f * t) return [x2, dx2dt] m = 0.5 # 質量[kg] k = 10000 # 剛性[N/m] c = 0.5 # 減衰係数[N・s/m] A = 100 # 強制外力の振幅[N] state0 = [0.0, 0.0] # 初期値[x0, v0] t0 = 0 # 初期時間[s] tf = 5 # 終了時間[s] dt = 0.005 # 時間刻み[s] t = np.arange(t0, tf + dt, dt) # 時間軸配列 f = np.arange(0, 100, 2) # 周波数リスト # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Displacement [m]') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('Displacement [m]') # データの範囲と刻み目盛を明示する。 ax2.set_xticks(np.arange(0, 10000, 100)) ax2.set_xlim(10, 100) # 対数スケール設定 ax2.set_xscale("log") ax2.set_yscale("log") y =[] for i in f: sol = odeint(func, state0, t, args=(m, k, c, A, i)) ax1.plot(t, sol) rms = np.sqrt(np.mean(sol ** 2)) y.append(rms) y = np.array(y) ax2.plot(f, y) fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
実行結果
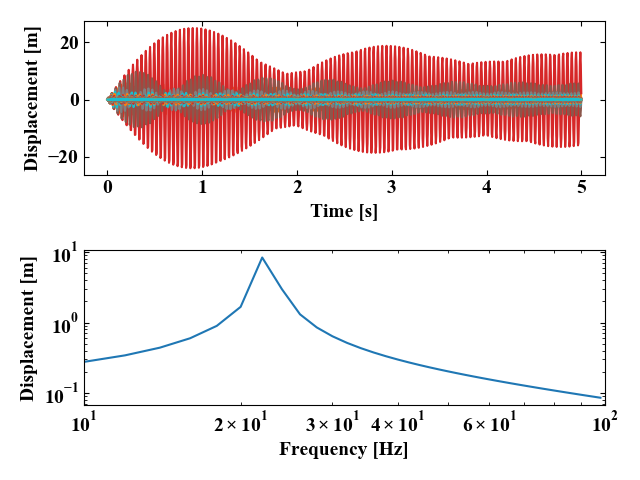
以下が実行結果です。上に時間波形、下に周波数波形を示しています。
固有振動数は22[Hz]ほどですので（np.sqrt(k/m)/(2*np.pi)）で調べてみて下さい）、周波数波形は22[Hz]の部分でピークを持っています。
過渡応答解析なので、時間波形は振幅が安定していない様子です。定常状態としてのモデルの挙動を調べたい時は、やはりモード法とかを使う方が良いでしょう。
安定するかどうかは加振力として与えている入力波形も大きく影響しているみたいです。その辺の話は「Pythonの過渡応答解析で力を滑らかにかけて応答の違いを見る」でまとめました。
そしてこの解析、約50回の数値計算を行い、それぞれ5[s]ものデータを持っています。普通のノートPCでトータルで2分ほど計算時間がかかってしまっていますので（1自由度なのに）、効率の面でもモード法を使った方が良さそうです。
まとめ
これまで覚えた振動モデルの解き方（過渡解析）を使って、周波数応答を求めてみました。
本来過渡応答はモデルの非線形な応答を調べたり、制御タイミングの検討をしたりといった目的で使われるので、今回の目的だったらかなり効率の悪い計算方法とわかりました。
一応この方法でも周波数応答は見れるよ、という結果になりましたね。
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント