
構造物の代表的な振動解析に「固有値解析」というものがあります。多自由度系の固有値解析は振動で問題になる固有振動数と振動モードの形を計算することができるため、世間で広く活用されています。ここではPythonによる振動の固有値解析方法を紹介します。
こんにちは。wat(@watlablog)です。
振動といったらまずは固有値というほど、固有値解析はポピュラーです。ここではPythonを使って多自由度振動系の固有値解析を自分で組めるレベルを目指します!
僕は振動の学習を「長松昭男, 実用モード解析入門, コロナ社※Amazon」で進めています。この書籍は僕が知る中で最も丁寧に、1自由度の振動系から話が始まり、実験の方法や実用的な内容が豊富で振動の勉強入門者にオススメです!
そして次に有用なのが「金子成彦, 大熊政明, 機械力学ハンドブック, 朝倉書店※Amazon」で、少々お高い(¥15,000くらい!)ですが、非線形の話や制御の話を含めて体系的に機械力学全般を網羅できるので、上記の長松先生の書籍と併せて読むことで振動に対する理解が深まります。僕は決して高い買い物ではなかったと感じています。
このページでは、上記書籍から得た知識を使ってPythonコード化します!
※書籍にはプログラムの話はありませんのでご注意下さい。
多自由度系の固有値解析概要
多自由度振動系とは?
固有値解析の話をする前に、今回対象とする多自由度振動系について紹介します。
「Pythonで1自由度非減衰系の自由振動シミュレーション」では、以下の画像に示す1つの質点の振動について学びました。質点が1つなので、このモデルの自由度は1自由度です。
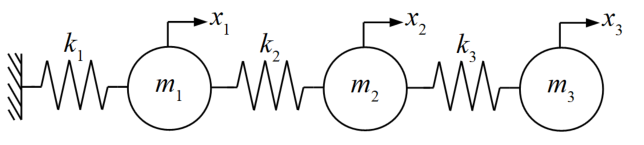
一方、多自由度振動系とは、質点が1つではなく複数ある系のことを呼びます。以下のモデルは質点が3つある3自由度の振動系であり、1自由度のばねマスが3つ直列に繋がったモデルとなっています。これらの質点は連成して振動します。
多自由度振動系モデルを取り扱うメリットは?
通常、振動の問題を議論する対象はビルや橋等の建造物や、車等の機械をはじめ多くが実際に存在する構造物です。
実在する構造物は全て連続体と言って、先に紹介した質量が集中している離散点があったり、無質量のばねで繋がっていたりはしません。実際には質量は構造物の中に分布されているし、材料によってはフックの法則に従わないばね定数も持ちます。
しかし、何かモノをつくる時に、「つくってみなければわからない」という安全性を確かめないで製品をリリースすることは世間的に許されません!
例えば、下の画像のように橋をつくろうとした場合を考えます。橋は「梁」で表現できるような連続体です。

橋は、その上を車が通行する時の加振、風がつくるカルマン渦による加振、地震による加振…と様々な外部加振による破壊の危険が予測されます。
振動には共振と言って構造物が持つ固有振動数が加振振動数と一致すると、非常に大きな振幅になってしまうという現象があります。これを避けるためには、予め構造物の固有振動数を予測される外部加振の振動数から十分離しておく設計をしなければなりません。
梁には連続体としての運動方程式がありますが、大規模な構造物に当てはめようとすると少々扱いがやっかいですので、一般には上の画像の右側のように、有限の自由度に離散化して考える手法がよく用いられます(ここでは簡略化のため、横振動を縦のばねで表現していますが…)。
この作業をモデル化と言ったりします。複雑な問題も適切に分解したり簡単にしたりして考えることで、いったい何Hzで共振するのか、その時はどんな形で振動するのか、といったシミュレーションがしやすくなるメリットがあります。
ここまで簡単にすれば、コンピュータで組めそうだぞ!
モデル化を行った後はコンピュータの出番です!
そして上で説明したような、何Hzで共振するのかという検討は「固有振動数」を指標に、どんな形で振動するのかの検討は「振動モード(固有ベクトル)」を指標にします。
そしてその検討は固有値解析を行うことで可能になります!
固有値解析の方法はとても簡単!
線形代数を復習しよう!
ここで説明する振動系の固有値解析とは、過去に紹介した線形代数の固有値と固有ベクトルを求める方法に他なりません。当ブログの「Pythonで線形代数!固有値と固有ベクトルを求める」はその理解の助けになると思いますので、是非読んでみて下さい。
運動方程式を多自由度系に拡張しよう!
先ほど紹介した記事、「Pythonで1自由度非減衰系の自由振動シミュレーション」でも質点とばねの運動方程式を載せていますが、まだ1自由度しかありません。しかし、1自由度の振動をよく理解することは非常に重要であるため、まだ1自由度があやしいという方はこの記事を是非読んでみて下さい。
そして、振動系が多自由度になった場合の運動方程式の作り方は「Pythonで計算するために多自由度振動系を行列形式にする方法」に記載しました。ばねマスが連結された場合でも1自由度の時と同じ考え方で運動方程式を立てることができ、コンピュータで計算を行うために行列形式で記述しました。今回振動の固有値解析にはこの行列形式の式を使います。
運動方程式を固有値解析できる形に変形する
まず、多自由度系の運動方程式を行列形式で式(1)と置きます。固有値解析の場合、外力は考えないので\(\mathbf{0}\)とゼロベクトルを与えて自由振動の方程式にしています。
$$\mathbf{M}\mathbf{\ddot{x}}+\mathbf{K}\mathbf{x}=\mathbf{0} (1)$$
次に、この方程式の解を式(2)と仮定します。上図の多自由度振動系のモデルは明らかに振動するため、オイラーの公式を利用して\( \mathbf{x}=\mathbf{\Phi }e^{i\omega t}\)と解を仮定しています。
ここで\(\mathbf{\Phi }\)は全体の変位ベクトル、\(i\)は虚数、\(\omega\)は角速度、\(t\)は時間です。\(e^{i\omega t}\)とすることで微分がしやすい(\(e^x\)は微分しても形が変わらない)ので便利です。
\(\mathbf{x}\)を仮定した後は機械的にこれを微分して、速度ベクトル\(\mathbf{\dot{x}}\)と加速度ベクトル\(\mathbf{\ddot{x}}\)を求めます。
\[
\begin{cases}
\mathbf{x}=\mathbf{\Phi }e^{i\omega t} \\
\mathbf{\dot{x}}=i\omega \mathbf{\Phi }e^{i\omega t} \\
\mathbf{\ddot{x}}=-\omega^{2} \mathbf{\Phi }e^{i\omega t}
\end{cases} (2)
\]
次に式(2)と仮定した解を式(1)に代入して式(3)を得ます。
$$-\omega^{2} \mathbf{M}\mathbf{\Phi }e^{i\omega t}+\mathbf{K}\mathbf{\Phi }e^{i\omega t}=\mathbf{0} (3)$$
式(3)は\(e^{i\omega t}\)で両辺を除することで消すことができ、\(\mathbf{M},
\mathbf{K}\)に共にかかっている\(\mathbf{\Phi }\)でくくり、順番を整理すると、式(4)を得ます。
$$\left ( \mathbf{K}-\omega^{2} \mathbf{M} \right )\mathbf{\Phi }=\mathbf{0} (4)$$
この形、よく見ると「Pythonで線形代数!固有値と固有ベクトルを求める」で紹介した式、\(\left ( A- \lambda I \right ) \vec{x}= \vec{0}\)と似たような形をしていますね。この式は\(\lambda\)が固有値、\(\vec{x}\)が固有ベクトルです。
但し、固有値\(\lambda\)のかかっている行列が単位マトリクス\(\mathbf{I}\)ではありません。この問題は一般固有値問題と呼ばれ、先ほどの記事に記載の方法で解くことができません。
※一方、固有値がかかっている行列が単位行列であれば、これは標準固有値問題と呼ばれます。
質量マトリクスが単位マトリクスなら解けるけどね。
一般固有値問題を標準固有値問題へ変換する
式(4)は一般固有値問題と呼ばれる方程式で、これを解く方法もあるようですが(PythonであればSciPyのlinalgで)、今回はせっかく覚えた標準固有値問題の解き方を使いたいので、式(4)を式(5)と変形させて一般固有値問題を標準固有値問題に変えて解きたいと思います。
$$\left ( \mathbf{M}^{-1}\mathbf{K}-\omega^{2} \mathbf{I} \right )\mathbf{\Phi }=\mathbf{0} (5)$$
質量マトリクスが単位マトリクスであれば、標準固有値問題になるので過去にやった方法で解けます。そのため質量マトリクスの逆行列\(\mathbf{M}^{-1}\)を算出して各項にかければ解決しますね。
Pythonで固有値解析をする!
2自由度の場合でプログラムを説明
いきなり3自由度以上のモデルで計算する前に、まずは2自由度でプログラムコードと結果の確認をしていきましょう。
モデルは以下の2自由度振動系です。
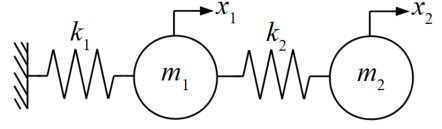
ブログ等のネットに載っている情報で答え合わせをしようと思ったのですが、中々このモデルの例題が大学の講義資料くらいしか見つかりませんでした。流石に大学の資料にリンクをかけるのは躊躇してしまったため、ここではそのパラメータをお借りするだけにします。
パラメータは\(m_{1}=50000[kg], m_{2}=50000[kg], k_{1}=30000000[N/m], k_{2}=20000000[N/m]\)です。これを固有値解析すると、\(\omega_{1}=14.14[rad/s], \omega_{2}=34.64[rad/s]\)が得られるとのこと。
それでは、プログラミングしてみましょう!
インポートするパッケージ
インポートするパッケージは行列演算に使用するNumPyと、グラフを使ってモードシェイプを見るためのmatplotlib。
|
1 2 |
import numpy as np from matplotlib import pyplot as plt |
この2つは毎回使っているからお馴染みだね。
パラメータと行列の作成
以下のコードはパラメータ設定と行列の作成部分です。
質量と剛性には先ほどのパラメータを設定します。そして運動方程式から求められた質量マトリクスと剛性マトリクスを作成します。
一般固有値問題(式(4))を標準固有値問題(式(5))にするために必要な質量マトリクスの逆行列もここで作成しておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# パラメータを設定 m1 = 50000 m2 = 50000 k1 = 30000000 k2 = 20000000 # 質量マトリクスと剛性マトリクスを作成 M = np.array([[m1, 0], [0, m2]]) K = np.array([[k1 + k2, -k2], [-k2, k2]]) # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) print(M) print(K) |
固有値と固有ベクトルを計算する
固有値と固有ベクトルの計算には「Pythonで線形代数!固有値と固有ベクトルを求める」で紹介した方法と全く同じですが、引数にはnp.dotを使って質量マトリクスの逆行列を剛性行列に掛けています。
計算された固有値は順番が必ずしも小さい数値から出てくるとは限りませんので、np.sortでソートしています。
但し、固有ベクトルは固有値と対応した数値をとらなければいけないので、np.argsortで固有値の並べ替えに使用された指標(インデックス)番号を取得しておき、for文を使って元の固有ベクトル配列の並べ替えを行っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソート omega_sort = np.sort(omega) # 固有値のソート時のインデックスを取得 # ⇒固有ベクトルと対応させるため sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) # 結果をコンソールに表示 print(np.sqrt(omega_sort)) print(v_sort) |
この並べ替え部分は、固有ベクトルの中身を良く理解していないと間違えそうなので注意が必要です。
ここでは、後でデータを抜き出しやすくするために転置してから抽出しています。
グラフに振動モードをプロット
固有ベクトルは数値だけだとよくわからないので、グラフにプロットして確認します。
グラフ化のために、横軸として自由度を作成します。モデル上は\(m_{1}, m_{2}\)の2自由度ですが、0として固定端も可視化しておいた方が理解しやすくなりますね。
for文でプロットをしていますが、これは固有ベクトルの先頭に固定端として動かない点を挿入しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 |
# グラフ化のために自由度軸を作成 dof = np.linspace(0, len(sort_index), len(sort_index)+1) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(6,3)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Degree of freedom') ax1.set_ylabel('Eigenvector') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 3, 1)) ax1.set_yticks(np.arange(-2, 2, 0.5)) ax1.set_xlim(0, 2) ax1.set_ylim(-1, 1) vec_label = ["$\omega_{1}$", "$\omega_{2}$"] # データプロット 固有ベクトルの形を見る for i in range(len(sort_index)): eigen_vector = np.concatenate([[0], v_sort[i]]) ax1.plot(dof, eigen_vector, label=vec_label[i], lw=1, marker='o') fig.tight_layout() plt.legend() # グラフを表示する。 plt.show() plt.close() |
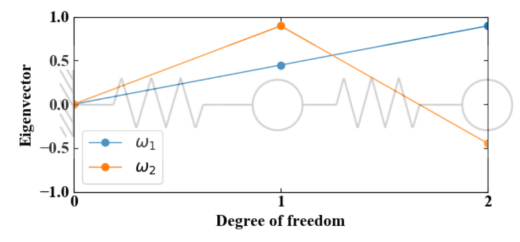
これらのコードを実行すると、以下のテキストがコンソールに表示されます。\(\omega_{1}=14.14, \omega_{2}=34.64\)となっており、大学の講義資料で確認した数値と同じになっていました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
# 質量マトリクス [[50000 0] [ 0 50000]] # 剛性マトリクス [[ 50000000 -20000000] [-20000000 20000000]] # 固有値(固有角振動数[rad/s]) [14.14213562 34.64101615] # 固有ベクトル(振動モードの形=モードシェイプ) [[ 0.4472136 0.89442719] [ 0.89442719 -0.4472136 ]] |
以下の図はプロットの結果です。この結果から\(\omega_{1}\)の振動は片持ち梁の1次、\(\omega_{2}\)は片持ち梁の2次モードにそっくりな形状になっていることがわかります。この形のことを振動モード、あるいはモードシェイプと呼んだりします。
3自由度の場合でも結果を見てみる(全コード付き)
後に記載する全コード内に示すパラメータの通り、3自由度目を追加すると以下の結果を得ます。3自由度あることによって1つ節が増えましたね。
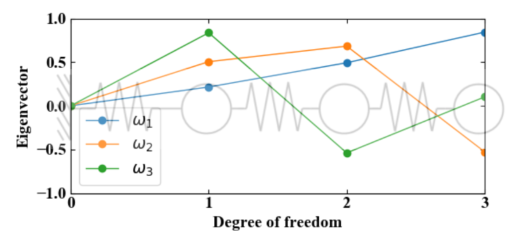
以下に3自由度の場合で書き換えた全コードを示します。パラメータを追加し、マトリクスを修正すればどんどん自由度を増やしていくことも可能です。剛性マトリクスの作り方は「Pythonで計算するために多自由度振動系を行列形式にする方法」を参照して頂ければと思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
import numpy as np from matplotlib import pyplot as plt # パラメータを設定 m1 = 50000 m2 = 50000 m3 = 50000 k1 = 30000000 k2 = 20000000 k3 = 10000000 # 質量マトリクスと剛性マトリクスを作成 M = np.array([[m1, 0, 0], [0, m2, 0], [0, 0, m3]]) K = np.array([[k1 + k2, -k2, 0], [-k2, k2 + k3, -k3], [0, -k3, k3]]) # 質量マトリクスの逆行列を計算 M_inv = np.linalg.inv(M) print(M) print(K) # 固有値と固有ベクトルを計算 omega, v = np.linalg.eig(np.dot(M_inv, K)) # 固有値の順番を昇順にソート omega_sort = np.sort(omega) # 固有値のソート時のインデックスを取得 # ⇒固有ベクトルと対応させるため sort_index = np.argsort(omega) # 固有値に対応する固有ベクトルをソート v_sort = [] for i in range(len(sort_index)): v_sort.append(v.T[sort_index[i]]) v_sort = np.array(v_sort) # 結果をコンソールに表示 print(np.sqrt(omega_sort)) print(v_sort) # グラフ化のために自由度軸を作成 dof = np.linspace(0, len(sort_index), len(sort_index)+1) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(6,3)) ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Degree of freedom') ax1.set_ylabel('Eigenvector') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(0, 4, 1)) ax1.set_yticks(np.arange(-2, 2, 0.5)) ax1.set_xlim(0, 3) ax1.set_ylim(-1, 1) # データプロット 固有ベクトルの形を見る for i in range(len(sort_index)): eigen_vector = np.concatenate([[0], v_sort[i]]) ax1.plot(dof, eigen_vector,lw=1, marker='o') fig.tight_layout() plt.legend() # グラフを表示する。 plt.show() plt.close() |
まとめ
今回は振動の代表的な解析手法である固有値解析について取り上げました。
ただ単に解析コードを紹介するだけでなく、多自由度振動系のモデル概要と、運動方程式の立て方、数学としての固有値と固有ベクトルの意味も包括した内容を目指しました。
数学上は解けるけど、物理的にはどんな意味があるかわからないといった学生さんや、普段固有値解析は商用ソフトに任せているから、自分で解いたことは無いという若手エンジニアさん(数日前の僕がそうです)に宛てて書いたつもりです。
固有値解析は何も振動の世界だけではなく、統計学を始め様々な分野で使われています。是非これをきっかけに色々な分野をのぞいてみて下さい!
固有値解析、簡単なモデルだけど自分でコーディングすると今までの理解がいっそう深まる!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント