
プロットを動的に可視化するのは現象の理解を助けたり、データを視覚的にアピールする時に役立ちます。ここでは楕円方程式の軌跡を描くことで、matplotlibのArtistAnimation関数の使い方を習得します。
こんにちは。wat(@watlablog)です。
データを動かしたい!そんな時もありますよね。ここではmatplotlibで動的なグラフ描画をする方法を学びます!
動的グラフの描き方
今回目標とするプロット
以下のGIFアニメーションの動的プロットを作成することを目標とします。
今回は予めデータを用意しておき、それを動画にする方法を紹介します。
※リアルタイム描画はまた別の方法があるそうです。
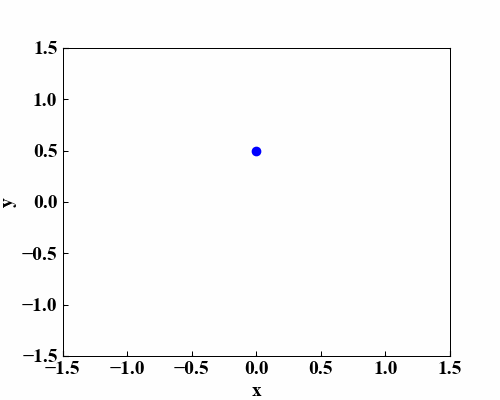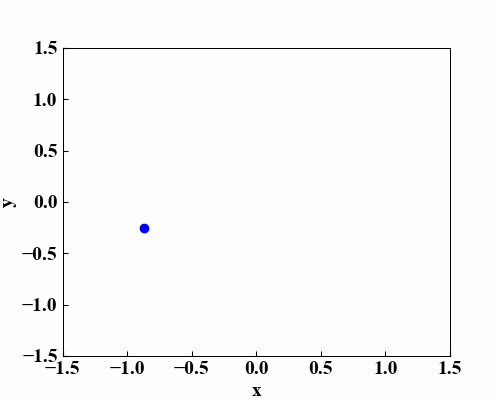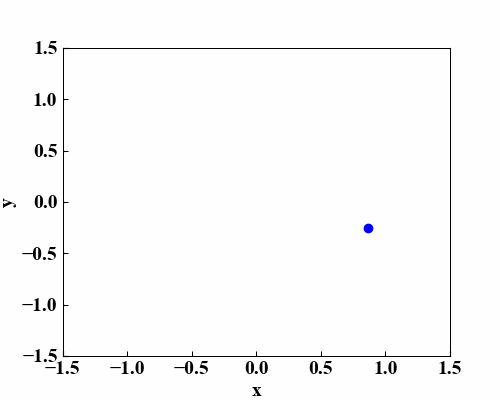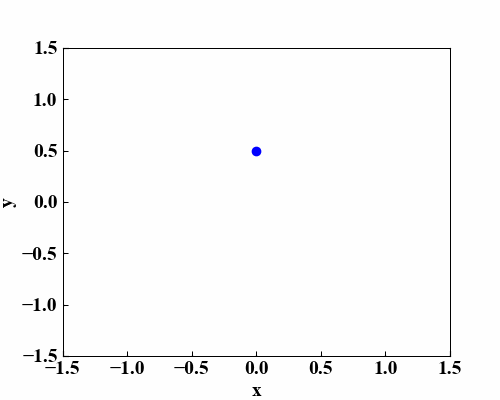
このプロットは、「Python/NumPyで楕円方程式を描画する!」で楕円を描いたものです。楕円方程式の式やプログラムコードはこの記事を参照して下さい。
アニメーションプロットのコード内容
データを動的に動かす場合、必要なものはアニメーションで動かす分だけの「フレーム」です。
以下の図が今回Pythonプログラムでコーディングする内容です。最終的にはGIFファイルを作成します。
必要な数だけのフレームとは、グラフプロットそのもののことですが、初めに全ての点を描画してしまっては動きを表現することはできません。
そのため、下図のようにデータ配列(今回は\(x, y\))に格納した1つ1つの数値を各フレームで取り出してプロットを絵として用意することが必要になります。
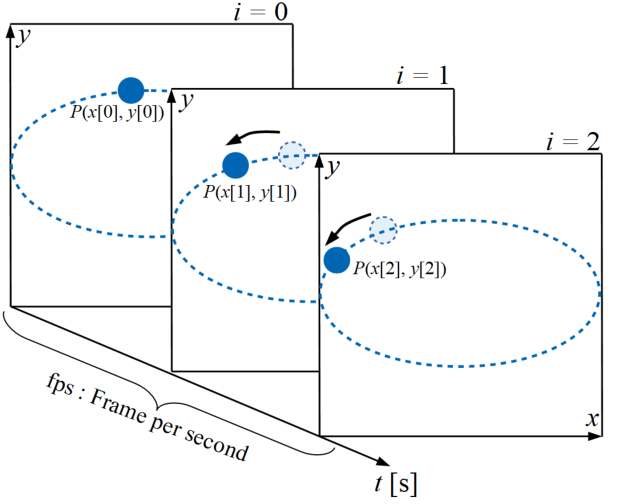
そしてアニメーションにするためには時間の情報も必要です。アニメーションはフレームをパラパラ漫画のように任意の時間間隔で更新することで表現しているので、速度を指定する必要があります。
この速度はfps(Frame per second)と呼ばれ、1秒間に何枚のフレームを表示させるかを意味します。一般的なデジカメの動画とかは30fpsとかですね。
それではこの内容をPythonでコーディングしていきます!
Pythonによるアニメーションプロットのコード
インポートするパッケージ
今回は楕円方程式の軌跡をプロットしていくので、NumPy、グラフプロットが必要なのでmatplotlibのpyplot、アニメーション用にmatplotlibのanimationをインポートします。
そしてインポート文こそ必要は無いですが、GIF動画作成に「Pillow」を使いました。僕の環境はAnacondaを使っていないので、「python -m pip install pillow」でインストールする必要がありました。
pipについての詳細は「Pythonのパッケージ管理ツール pipの使い方とコマンド集」を是非参照下さい。
|
1 2 3 |
import numpy as np from matplotlib import pyplot as plt from matplotlib import animation |
ちなみにGIF動画作成は一般的にImageMagickという外部ライブラリを使う方が多いようですが、虚弱性も報告されているという噂を見つけてしまったので、僕はそれを使わずPillowを選択しました。
しかし一方で、 ImageMagick には脆弱性が大量に存在します。2017 年に報告された ImageMagick の脆弱性は 236 件 でした。大量にある上にリモートコード実行級の脆弱性もあり、安全性という観点ではかなり厳しい評価をしなければなりません。こちらに ImageMagick の脆弱性情報があり、その多さが伺えると思います。
Cybozu:さようならImageMagic:https://blog.cybozu.io/entry/2018/08/21/080000
プロット用データ作成用関数(for文で用意)
プロットに使う楕円の座標計算関数を用意します。この関数は横軸\(x\), 楕円パラメータ\(a, b\), \(x\)の勾配\(g\)を引数にしています。
楕円の縦軸値である\(y\)とアニメーション用プロットのフレームであるimgsは空の配列を用意しておいてfor文の中で逐次配列に要素を追加していくという方法です。
符号スイッチ\(c\)は勾配の符号が変わったら\(y\)軸の象限変更を行うので、そのきっかけに用意しました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 |
def ellipse(x, a, b, g): y = [] # y値をためる imgs = [] # プロットをためる入れ物 c = 1 # y軸の符号スイッチ # 第1象限から第4象限までの全てのy値を計算 for i in range(len(g)): y_single = b * np.sqrt(1 - (np.power(x[i], 2) / np.power(a, 2))) if i == 0: pass elif np.sign(g[i - 1]) == np.sign(g[i]): pass else: c = -1 * c y.append(y_single * c) # y値の符号調整 # グラフ描画 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' plt.xlabel('x') plt.ylabel('y') plt.xticks(np.arange(-2, 2, 0.5)) plt.yticks(np.arange(-2, 2, 0.5)) plt.xlim(-1.5, 1.5) plt.ylim(-1.5, 1.5) # アニメーション用データ作成 img = plt.plot(x[i], y[i], 'b-o') imgs.append(img) return y, imgs # 楕円軌道のy値と、アニメーション用プロットを返す |
グラフの設定もこの関数の中で行います。戻り値には楕円の\(y\)値とプロットフレームをまとめたimgsを指定しています。
その他パラメータと関数実行文
楕円のパラメータと横軸\(x\)の振動のさせ方を設定した後、関数を実行する前にfigure関数でプロットの入れ物オブジェクトを作っておきます。ついでにグラフのサイズを指定しています。
ここまでが準備で、先ほど作成した楕円関数を実行します。
|
1 2 3 4 5 6 7 8 9 10 |
a = 1.0 # 楕円方程式のa b = 0.5 # 楕円方程式のb t = np.linspace(-1 * np.pi, np.pi, 100) # -π~πまでの範囲 phase = 0 # 位相 x = a * np.sin(t - phase) # 1周期分の正弦波を作成 g = np.gradient(x) # xの勾配を計算 fig = plt.figure(figsize = (5, 4)) # プロットにためる前にfigureを作っておく y, imgs = ellipse(x, a, b, g) # 楕円軌道のプロットデータを関数で計算 |
アニメーションの作成とGIF保存
最後にアニメーションプロットの表示とGIFファイルへの保存を以下のコードで行います。
|
1 2 3 4 5 6 7 |
# アニメーションを作る ani = animation.ArtistAnimation(fig, imgs, interval=10) ani.save('ellipse.gif', writer = 'pillow', fps = 30) # グラフを表示する plt.show() plt.close() |
ここまでのコードを全て貼り付け、実行することで本ページの上に添付したGIF動画が出来ます。
※GIFファイル編集ソフトで単純に開き再度保存することでファイルサイズが軽くなったのですが、もしかすると他にも色々設定できる所があるかも知れません。
まとめ
楕円方程式の軌跡をアニメーションでプロットし、GIFファイルを作成する方法を習得しました。
データの作り方や扱い方に少しくせがありますが、視覚的にデータを表示する効果はやはり大きいと思います。
関数の「軌跡」を描くプログラムができたぞ!実はこの関数は後程画像処理で応用させたい案件なので、そのうち紹介します!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!
全コード
コピペがしやすいように、上で分割記載しているコードを1つにまとめてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 |
import numpy as np from matplotlib import pyplot as plt from matplotlib import animation def ellipse(x, a, b, g): y = [] # y値をためる imgs = [] # プロットをためる入れ物 c = 1 # y軸の符号スイッチ # 第1象限から第4象限までの全てのy値を計算 for i in range(len(g)): y_single = b * np.sqrt(1 - (np.power(x[i], 2) / np.power(a, 2))) if i == 0: pass elif np.sign(g[i - 1]) == np.sign(g[i]): pass else: c = -1 * c y.append(y_single * c) # y値の符号調整 # グラフ描画 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' plt.xlabel('x') plt.ylabel('y') plt.xticks(np.arange(-2, 2, 0.5)) plt.yticks(np.arange(-2, 2, 0.5)) plt.xlim(-1.5, 1.5) plt.ylim(-1.5, 1.5) # アニメーション用データ作成 img = plt.plot(x[i], y[i], 'b-o') imgs.append(img) return y, imgs # 楕円軌道のy値と、アニメーション用プロットを返す a = 1.0 # 楕円方程式のa b = 0.5 # 楕円方程式のb t = np.linspace(-1 * np.pi, np.pi, 100) # -π~πまでの範囲 phase = 0 # 位相 x = a * np.sin(t - phase) # 1周期分の正弦波を作成 g = np.gradient(x) # xの勾配を計算 fig = plt.figure(figsize = (5, 4)) # プロットにためる前にfigureを作っておく y, imgs = ellipse(x, a, b, g) # 楕円軌道のプロットデータを関数で計算 # アニメーションを作る ani = animation.ArtistAnimation(fig, imgs, interval=10) ani.save('ellipse-course.gif', writer = 'pillow', fps = 30) # グラフを表示する plt.show() plt.close() |

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント