ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
前回はニューラルネットワークの基礎であるパーセプトロンでANDゲートを作ってみました。さらなる理解のために、今回はOR回路を作って同じように特性をみてみます。
こんにちは。wat(@watlablog)です。
ディープラーニングを理解するために、引き続きパーセプトロンを学びます。
ここでは論理回路の1つであるOR回路をパーセプトロンで実装します。
パーセプトロンについては様々なWebページで紹介がされていますが、本記事は「斎藤康毅, ゼロから作るDeep Learning, オライリー・ジャパン, (2016), pp.21-27」で学んだ内容を元に、自分なりのコーディングをした結果をまとめています。式の解釈等詳細は書籍をご参照下さい。
パーセプトロンでORゲートを作る！
ORゲートとは？
前回の記事「PythonでパーセプトロンのANDゲートを実装する！」でパーセプトロンの概要と論理回路、ANDゲートについては簡単に説明しました。今回は前回の話を前提に進みますので、もしよろしければご覧下さい。
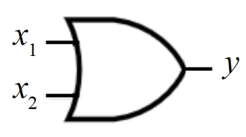
今回はORゲートについてパーセプトロンで調べていきます。ORゲートとは、論理回路の1つで「論理和」を意味します。図にすると以下のようにANDゲートと異なり少しとがった形をしています。
真理値表は以下の表です。入力の中で少なくとも1つが1であれば1を出力するという回路です。
| \(x_{1}\) | \(x_{2}\) | \(y\) |
| 0 | 0 | 0 |
| 0 | 1 | 1 |
| 1 | 0 | 1 |
| 1 | 1 | 1 |
パーセプトロンによるORゲートのコーディング
ANDゲートで一度Python標準関数による出力確認は実施したので、今回は飛ばして、いきなりパーセプトロンによるコーディングに入ります。
作ったのは以下の2入力のパーセプトロン関数です。ANDゲートの時に使った関数と全く同じものです。
|
1 2 3 4 5 6 7 8 |
#2入力パーセプトロンの関数 def perceptron(x1, x2, w1, w2, theta): f = w1 * x1 + w2 * x2 if f <= theta: y = 0 else: y = 1 return y |
この単純ニューラルネットワークは重み\(w\)と閾値\(\theta\)で出力の特性を変える、というのが強みなので引き続きパラメータの調整作業を行います。
以下が本文です。w1, w2, thetaに入っている値がORゲートの特性を実現するためのパラメータです。ANDの時と同様に組み合わせは無限にあります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
import numpy as np x1 = np.array([0, 0, 1, 1]) x2 = np.array([0, 1, 0, 1]) w1 = 0.5 w2 = 0.5 theta = 0.2 for i in range(4): X1 = x1[i] X2 = x2[i] y = perceptron(X1, X2, w1, w2, theta) print(y) >0 >1 >1 >1 |
これを実行すると0, 1, 1, 1と真理値表通りの応答が得られるはずです。
さらに入力範囲を拡張してみる
ANDと同様に入力範囲を0と1以外に拡張してみます。するとやはりある所で線を引くことができ、その線を境に0と1が切り替わります。
パーセプトロンで作ったORゲートはこの1つの側面を見ているに過ぎないんですね。
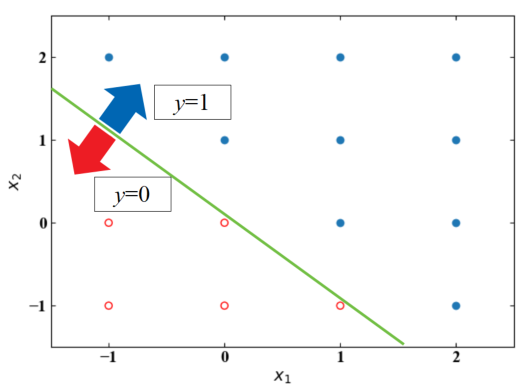
上図の分布図は以下のコードで得ることができます。パラメータが異なるだけですが、詳しくは前回のANDゲートの記事を参照下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 |
import numpy as np from matplotlib import pyplot as plt #2入力パーセプトロンの関数 def perceptron(x1, x2, w1, w2, theta): f = w1 * x1 + w2 * x2 if f <= theta: y = 0 else: y = 1 return y x1 = np.array([0, 0, 1, 1, 0, 1, -1, -1, -1, 2, 0, 2, 1, 2, -1, 2]) x2 = np.array([0, 1, 0, 1, -1, -1, 0, -1, 1, 0, 2, 1, 2, 2, 2, -1]) w1 = 0.5 w2 = 0.5 theta = 0.2 #プロット用の配列（P0がy=0, P1がy=1の座標を入れるための配列） P0_x = [] P0_y = [] P1_x = [] P1_y = [] #プロット用にデータを分類し格納する。 for i in range(16): X1 = x1[i] X2 = x2[i] y = perceptron(X1, X2, w1, w2, theta) print(y) if y == 0: P0_x.append(x1[i]) P0_y.append(x2[i]) else: P1_x.append(x1[i]) P1_y.append(x2[i]) P0_x = np.array(P0_x) P0_y = np.array(P0_y) P1_x = np.array(P1_x) P1_y = np.array(P1_y) # ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('$x_{1}$') ax1.set_ylabel('$x_{2}$') # データの範囲と刻み目盛を明示する。 ax1.set_xticks(np.arange(-3, 3, 1)) ax1.set_yticks(np.arange(-3, 3, 1)) ax1.set_xlim(-1.5, 2.5) ax1.set_ylim(-1.5, 2.5) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.scatter(P0_x, P0_y, facecolors = 'none', edgecolors = 'r', label='$y=0$', lw=1) ax1.scatter(P1_x, P1_y, label='$y=1$', lw=1) fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
<広告>
人工知能のプロに最速でなるには、独学よりも効果的なオンラインゼミがあります。これを機会に是非ご検討下さい！
まとめ
このページではANDゲートに引き続き、ORゲートをパーセプトロンで実装してみました。
中身はパラメータ以外全くANDゲートと同じという、ちょっと拍子抜けするような記事になってしまいましたが、パラメータ以外は全く同じという部分に可能性を感じます。
歴史を見るとパーセプトロンは一度は下火になったアルゴリズムですが、現代ではこのアルゴリズムを基礎において、多層、4層以上でも学習を進めるためのディープネットワーク、活性化関数等工夫がされ盛り上がってきています。
何事も基礎をしっかり身に着けることは重要です。ディープラーニングにいきなり飛びつく前に、1層、3層等で十分経験を積んでみよう！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント