
ローパス、ハイパスフィルタの応用となるバンドパスフィルタは信号のノイズ除去以外にも、特徴量の抽出に役立ちます。フィルタには実際難しい理論がありますが、PythonのSciPyなら簡単に使うことが可能です。
こんにちは。wat(@watlablog)です。
これまで学んだフィルタ処理の応用編として、このページではバンドパスフィルタを紹介します!
バンドパスフィルタについて
バンドパスフィルタとは?
WATLABブログでは前回までに、高周波帯域ノイズを除去したい時に使うローパスフィルタ、低周波帯域の信号をキャンセルして高周波帯域成分を抽出するハイパスフィルタをPythonでコーディングして来ました。
今回はその両方の特性を持つバンドパスフィルタ(band-pass filter)を紹介します。
バンドパスフィルタとは、ある周波数幅(バンド)のみの信号を通過(パス)させるフィルタのことで、ローパスフィルタとハイパスフィルタの組み合わせによって構成されます。
バンドパスフィルタは光学の分野でよく使われており、特定波長の光のみを抽出する目的で利用されます。
しかし、「特定の周波数帯域だけを通す」という機能は、工学的にも幅広い用途があるためあらゆる場面で活用されています。
バンドパスフィルタで重要な因子と用語(図解)
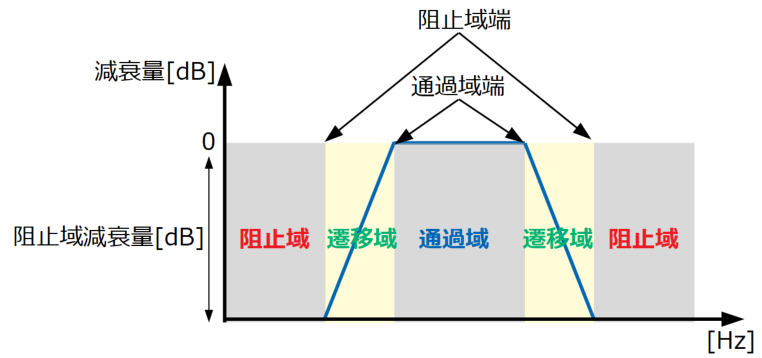
バンドパスフィルタはある周波数幅の帯域だけを通過させるため、以下の図のように1つの通過域がありますが、阻止域と遷移域が2つあるのが特徴です。
そのため、通過域端と阻止域端が2つずつあることになり、これまでのローパスフィルタやハイパスフィルタと比べるとプログラムする上で設定項目が増えることになります。
今回もバターワースフィルタを例にコーディングしていきます。
PythonのSciPyバンドパスフィルタ
ソースコード
メインファイル
ソースコードを以下に示します。フィルタ処理を実際に行う部分はdef文を使って関数化しました。関数の使い方については「Pythonの関数def文の使い方!引数や別ファイル式も解説」の記事に詳細を示しています。
まずはメイン(main_filter.py)のコードです。
サンプルとしてガウシアンノイズを生成していますが、こちらについては「Pythonでガウス分布を持つノイズの作り方と調整方法」の記事を参照下さい。
中身ですが、ローパスやハイパスの時とパラメータの種類は同じです。しかし通過域端周波数fpと阻止域端周波数fsは上図の理由で2つあるので、以下のコードのようにベクトル形式で入力する必要があります。そしてこのベクトルはNumPy形式で記述する必要があるため、np.arrayを使っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 |
import filter_function import numpy as np from matplotlib import pyplot as plt samplerate = 25600 x = np.arange(0, 12800) / samplerate # 波形生成のための時間軸の作成 data = np.random.normal(loc=0, scale=1, size=len(x)) #ガウシアンノイズを生成 fp = np.array([1000, 3000]) #通過域端周波数[Hz]※ベクトル fs = np.array([500, 6000]) #阻止域端周波数[Hz]※ベクトル gpass = 3 #通過域端最大損失[dB] gstop = 40 #阻止域端最小損失[dB] data_filt = filter_function.bandpass(data, samplerate, fp, fs, gpass, gstop) |
関数ファイル
関数ファイル(filter_function.py)もローパスやハイパスとほぼ同じです。signal.butterでbandを指定する所が変化点です。
|
1 2 3 4 5 6 7 8 9 |
#バターワースフィルタ(バンドパス) def bandpass(x, samplerate, fp, fs, gpass, gstop): fn = samplerate / 2 #ナイキスト周波数 wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化 ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化 N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算 b, a = signal.butter(N, Wn, "band") #フィルタ伝達関数の分子と分母を計算 y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける return y #フィルタ後の信号を返す |
参考:フーリエ変換まで含めた全コード
先ほどまではフィルタ処理の部分のみを解説していましたが、ファイルを2つ作ったり面倒だと思いますので、コピペしてすぐ動かせる全コードを以下に示します。
このコードはサンプル波形を生成して、フーリエ変換とデシベル変換を行っており、フィルタ前後の波形を比較する事が可能です。是非動かして遊んでみて下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 |
import numpy as np from scipy import signal from scipy import fftpack from matplotlib import pyplot as plt #バターワースフィルタ(バンドパス) def bandpass(x, samplerate, fp, fs, gpass, gstop): fn = samplerate / 2 #ナイキスト周波数 wp = fp / fn #ナイキスト周波数で通過域端周波数を正規化 ws = fs / fn #ナイキスト周波数で阻止域端周波数を正規化 N, Wn = signal.buttord(wp, ws, gpass, gstop) #オーダーとバターワースの正規化周波数を計算 b, a = signal.butter(N, Wn, "band") #フィルタ伝達関数の分子と分母を計算 y = signal.filtfilt(b, a, x) #信号に対してフィルタをかける return y #フィルタ後の信号を返す # オーバーラップ処理 def ov(data, samplerate, Fs, overlap): Ts = len(data) / samplerate # 全データ長 Fc = Fs / samplerate # フレーム周期 x_ol = Fs * (1 - (overlap / 100)) # オーバーラップ時のフレームずらし幅 N_ave = int((Ts - (Fc * (overlap / 100))) / (Fc * (1 - (overlap / 100)))) # 抽出するフレーム数(平均化に使うデータ個数) array = [] # 抽出したデータを入れる空配列の定義 # forループでデータを抽出 for i in range(N_ave): ps = int(x_ol * i) # 切り出し位置をループ毎に更新 array.append(data[ps:ps + Fs:1]) # 切り出し位置psからフレームサイズ分抽出して配列に追加 return array, N_ave # オーバーラップ抽出されたデータ配列とデータ個数を戻り値にする # 窓関数処理(ハニング窓) def hanning(data_array, Fs, N_ave): han = signal.hann(Fs) # ハニング窓作成 acf = 1 / (sum(han) / Fs) # 振幅補正係数(Amplitude Correction Factor) # オーバーラップされた複数時間波形全てに窓関数をかける for i in range(N_ave): data_array[i] = data_array[i] * han # 窓関数をかける return data_array, acf # FFT処理 def fft_ave(data_array, samplerate, Fs, N_ave, acf): fft_array = [] for i in range(N_ave): fft_array.append(acf * np.abs(fftpack.fft(data_array[i]) / (Fs / 2))) # FFTをして配列に追加、窓関数補正値をかけ、(Fs/2)の正規化を実施。 fft_axis = np.linspace(0, samplerate, Fs) # 周波数軸を作成 fft_array = np.array(fft_array) # 型をndarrayに変換 fft_mean = np.mean(fft_array, axis=0) # 全てのFFT波形の平均を計算 return fft_array, fft_mean, fft_axis #リニア値からdBへ変換 def db(x, dBref): y = 20 * np.log10(x / dBref) #変換式 return y #dB値を返す # ここからサンプル波形生成とフィルタ処理をする------------------------------------------- samplerate = 25600 x = np.arange(0, 12800) / samplerate # 波形生成のための時間軸の作成 data = np.random.normal(loc=0, scale=1, size=len(x)) # ガウシアンノイズを生成 fp = np.array([1000, 3000]) # 通過域端周波数[Hz]※ベクトル fs = np.array([500, 6000]) # 阻止域端周波数[Hz]※ベクトル gpass = 3 # 通過域端最大損失[dB] gstop = 40 # 阻止域端最小損失[dB] # バンドパスをする関数を実行 data_filt = bandpass(data, samplerate, fp, fs, gpass, gstop) # ------------------------------------------------------------------------------ # ここから平均化フーリエ変換とデシベル変換を行う---------------------------------------------- Fs = 4096 # フレームサイズ overlap = 90 # オーバーラップ率 # 作成した関数を実行:オーバーラップ抽出された時間波形配列 t_array_org, N_ave_org = ov(data, samplerate, Fs, overlap) t_array_filt, N_ave_filt = ov(data_filt, samplerate, Fs, overlap) # 作成した関数を実行:ハニング窓関数をかける t_array_org, acf_org = hanning(t_array_org, Fs, N_ave_org) t_array_filt, acf_filt = hanning(t_array_filt, Fs, N_ave_filt) # 作成した関数を実行:FFTをかける fft_array_org, fft_mean_org, fft_axis_org = fft_ave(t_array_org, samplerate, Fs, N_ave_org, acf_org) fft_array_filt, fft_mean_filt, fft_axis_filt = fft_ave(t_array_filt, samplerate, Fs, N_ave_filt, acf_filt) # dB変換する fft_mean_org = db(fft_mean_org, 2e-5) fft_mean_filt = db(fft_mean_filt, 2e-5) # ----------------------------------------------------------------------------------- # ここからグラフ描画--------------------------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(211) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(212) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('SP[Pa]') ax2.set_xlabel('Frequency [Hz]') ax2.set_ylabel('SPL[dB]') # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, data, label='original', lw=1) ax1.plot(x, data_filt, label='filtered', lw=1) ax2.plot(fft_axis_org, fft_mean_org, label='original', lw=1) ax2.plot(fft_axis_filt, fft_mean_filt, label='filtered', lw=1) plt.legend() # 軸のリミットを設定する。 ax2.set_xlim(0, max(fft_axis_org)/2) ax2.set_ylim(-20, 100) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # ----------------------------------------------------------------------------------- |
実行結果
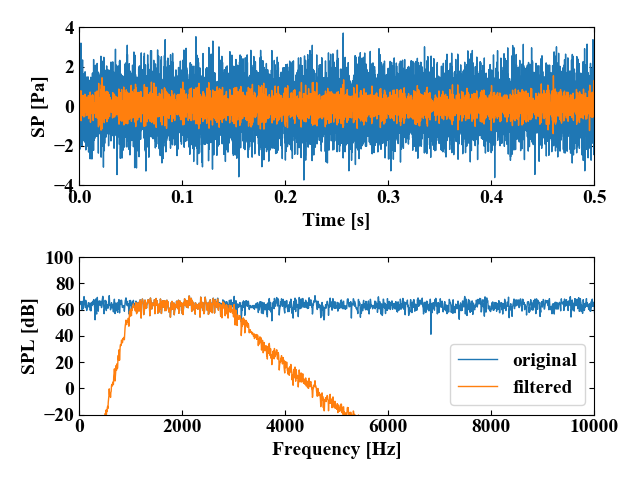
バンドパスフィルタをガウシアンノイズに対してかけた結果です。
下図上段が時間波形、下段が上段の波形をFFTした後の周波数波形です。それぞれフィルタ前(original)とフィルタ後(filtered)を比較しています。
ここではFFTやデシベル変換も使っていますが、それぞれの詳細は以下の記事にまとめていますので、是非ご覧ください。
PythonでFFT!SciPyのFFTまとめ
Pythonで音圧のデシベル(dB)変換式と逆変換式
これまでと同じように、ノイズ波形だけではつまらないので、サイン波を二つ合成させた波形を作って効果を確認していきます。
上のメインコード(main_filter.py)の波形生成部分とフィルタ周波数を以下のように変更してみます。
|
1 2 3 4 5 6 |
data = np.sin(2.0 * np.pi * 200 * x) + np.sin(2.0 * np.pi * 1000 * x) + 0.5 * np.random.normal(loc=0, scale=1, size=len(x)) #2つのサイン波とノイズ波を合成 fp = np.array([500, 1500]) #通過域端周波数[Hz]※ベクトル fs = np.array([250, 3000]) #阻止域端周波数[Hz]※ベクトル gpass = 3 #通過域端最大損失[dB] gstop = 40 #阻止域端最小損失[dB] |
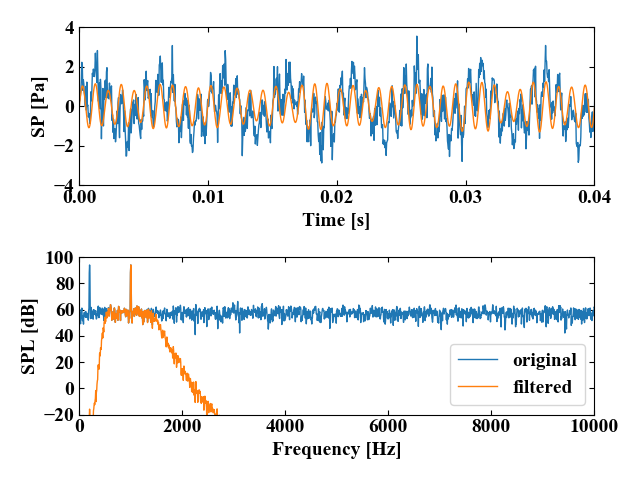
元波形は1000[Hz]の信号が200[Hz]でうねり成分を持ち、かつ全体的に高周波ノイズが含まれていましたが、バンドパスフィルタをかけたことで1000[Hz]の信号を比較的綺麗に抽出することができました。
まとめ
フィルタ処理の一種であるバンドパスフィルタをPythonで使えるようになりました。
バンドパスフィルタはローパスフィルタやハイパスフィルタと比べ阻止域が2つあるため、周波数の設定はベクトル形式で用意する必要がありました。
SciPyを使えばバンドパスフィルタを容易に設計できることを学びました。
バンドパスは特定の信号を抽出する用途で使うため、何か特徴量を抽出する分野では万能に使えそうだね!フィルタ処理の基礎もあと少し!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
質問失礼いたします。Python初心者です。
ソースコードを実行すると”name ‘signal’ is not defined”とエラーが吐き出されてしまいます。
signalは別で定義が必要ということでしょうか?
又は、scipyからimportすれば使用出来るのでしょうか?
おかしな質問でしたら申し訳ありません。
ご回答いただけると嬉しいです。
宜しくお願い致します。
ご訪問ありがとうございます。
signalはfrom scipy import signalとインポートします。
こちらのページでは省略していましたので、わかりにくかったかも知れません。
新しく「参考:フーリエ変換まで含めた全コード」という項目を書いてみました。
こちらのコードを貼り付けてそのまま動きますでしょうか?
よろしくお願い致します。
初心者ですが、ブログを楽しみにしています。ありがとうございます。
任意のcsvファイルのデータに対してバンドパスフィルタ(0.5Hz~30Hz)を使いたいと思っています。
この例はガウシアンノイズに対してバンドパスフィルタを用いたと思い、の部分を書き換えてみました。
用いたCSVファイルは、「ただPythonでcsvから離散フーリエ変換をするだけのコード」に載っていたcsvファイルを参考にしています。
—
samplerate = 1024
x = np.arange(0, 512) / samplerate
df_master = pd.read_csv(‘signals.csv’, index_col=0)
data = df_master.iloc[:,[2]]
fp = np.array([1, 30])
fs = np.array([0.5, 60])
gpass = 3
gstop = 40
—
すると、以下のエラーが出たのでてしまいましたがよく理解できません。gpass/gstopの値を変更すると、”45″の値は変化します。
The length of the input vector x must be greater than padlen, which is 45.
設定方法について、教えて頂けますか。(参考になるページでも嬉しいです。)
ご質問ありがとうございます。
こちらでエラーが再現せず回答が遅れてしまって申し訳ございません。
(解決されていましたら無視して下さい…)
そのエラーはベクトルの長さに関するもののようで、データ長に不整合があるようです。
xは新たに定義されていますが、csvはそのまま使っているのでしょうか?
「ただPythonでcsvから離散フーリエ変換をするだけのコード」を参考にして頂いているとのことで、
僕の方でこの記事で紹介しているコードをベースにバンドパスフィルタを追加して動作させてみたところ、特にエラーなく動作しました。
コード変更部分は以下です。
先頭にfrom scipy import signalを書き、バンドパスの関数を置いておいた上で、フーリエ変換前にフィルタ処理を追加しただけです。
# 列方向に順次フーリエ変換(DFT)をするコード
for i in range(len(df.T)-1):
print(i)
data = df.T.iloc[i+1] # フーリエ変換するデータ列を抽出
# フィルタ処理
fp = np.array([1, 30]) # 通過域端周波数[Hz]※ベクトル
fs = np.array([0.5, 60]) # 阻止域端周波数[Hz]※ベクトル
gpass = 3 # 通過域端最大損失[dB]
gstop = 40 # 阻止域端最小損失[dB]
data = bandpass(x=data, samplerate=1/dt,
fp=fp, fs=fs,
gpass=gpass, gstop=gstop)
data = pd.Series(data)
spectrum, amp, phase, freq = calc_fft(data.values, 1/dt) # フーリエ変換をする関数を実行
まずは上記記事のコードをベースに動かしてみて、必要であればカスタマイズをお試し頂ければと思います。
フィルタに関する質問は多いのと、どうやら他の質問サイト様でも需要がある様子がわかりましたので、別途まとめ記事を書こうと思います。
近日公開しますので、もしよろしければご確認下さい。
以上、よろしくお願い致します。
ありがとうございます。出来ました!
先日更新されていたブログも拝見しました。ありがとうございます。
ブログで紹介されていたPyQも始めてみました(^^ゞ。
ご連絡ありがとうございました。
問題ないようで安心しました!
PyQ色々なコンテンツあって面白いですよね。
是非今後もブログでわからない事やリクエストがありましたらご連絡ください!
初心者的な質問をして申し訳ありません。波形生成をする際に使用しているsamplerateは何を表しているのでしょうか。実際のデータにバンドパスフィルターをかけたいのですが何を対応させればよいのかが分からなくて困ってしまいました。
お忙しいと思いますがお答えいただけると幸いでございます。
ご訪問ありがとうございます。
samplerateとは、サンプルレート、サンプリングレートのことで、1秒当たりのデータポイント数を意味しています。
データを取得(サンプリング)する頻度(レート)のことで、例えば1秒間に1回データを取得する場合は1[Hz]になります。
実際のデータの横軸が0, 0.1, 0.2…の間隔になっている場合はサンプリングレートは10[Hz]というようなデータ間隔と対応させてみてください。
以上、その他不明点ございましたらお気軽にコメントください。