ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
Warning: Undefined array key "title" in /home/worldwalker/watlab-blog.com/public_html/wp-content/plugins/kattene/plugin.php on line 112
Warning: Undefined array key "title" in /home/worldwalker/watlab-blog.com/public_html/wp-content/plugins/kattene/plugin.php on line 112
ガウスの消去法は掃き出し法とも呼ばれ、機械的に連立1次方程式を解く方法で有名です。Pythonには様々な便利ライブラリがありますが、ここではNumpyだけを使ってガウスの消去法を書き、アルゴリズムの理解をすることを目標とします。
こんにちは。wat(@watlablog)です。ここでは連立1次方程式をプログラムで解くために、ガウスの消去法をゼロからPythonでコーディングします！
ガウスの消去法の概要
ガウスの消去法とは？
ガウスの消去法(Gaussian Elimination)とは、掃き出し法(Row Reduction)とも呼ばれ、連立1次方程式を解くアルゴリズムの1つです。
ガウスの消去法は以下のような連立1次方程式に対して使います。
この連立1次方程式は係数行列\(\mathbf{A}\)と定数ベクトル\(\mathbf{b}\)を使うと、以下のように表現することが可能です。
\mathbf{A}=\begin{bmatrix}
a_{11}& a_{12}& a_{13}& a_{14}\\
a_{21}& a_{22}& a_{23}& a_{24}\\
a_{31}& a_{32}& a_{33}& a_{34}\\
a_{41}& a_{42}& a_{43}& a_{44}\\
\end{bmatrix},
\mathbf{b}=\begin{bmatrix}
b_{1}\\
b_{2}\\
b_{3}\\
b_{4}
\end{bmatrix}
\]
また、拡大係数行列として以下の表記も可能です。
ガウスの消去法はこの拡大係数行列に対し、前進消去と後退代入という2つのステップを使って連立方程式の解を機械的に求めます。
前進消去
前進消去(Forward elimination)とは、先ほどの拡大係数行列に対し行基本操作を行い、係数行列の対角成分を1に、下三角を0に変形して階段行列(0が階段のように見えることが由来)を作ることです。
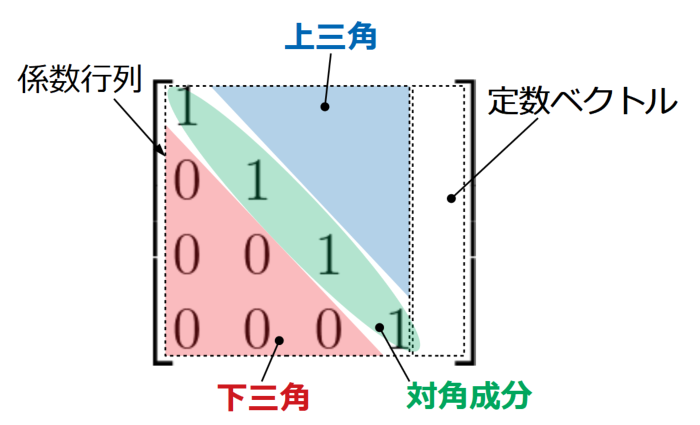
行基本操作とは、
①ある行を定数倍する。
②ある行を定数倍したものを他の行に加える。
③行を入れ替える。
といった操作で、これらの操作は方程式の意味を変えない変形であるため同値変形と呼ばれます。
学校で最初に連立方程式を教わった時に学ぶ方法ですね！この同値変形は方程式がいくつになろうと成立します。
後退代入
後退代入(Backward substitution)とは、前進消去で作り上げた階段行列に対して行う操作で、連立1次方程式の求解部分のことです。
階段行列の最下段は係数行列の左側が全て0、右端が1になっています。その右隣は定数項なので、既に解が得られている段となります。
最下段の解がわかれば、その1つ上の段の未知数も計算可能になるため、以下の図のようにドミノ倒し的に解を求めることができます。下から代入していって解を求めることから、後退代入という名称が付いています。
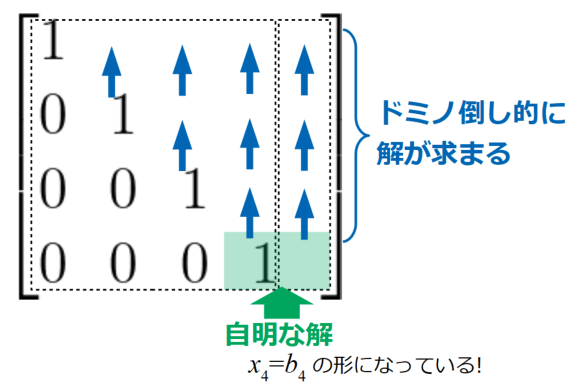
よく使われる所
教科書や受験レベルの数学問題は手計算によって解くことが前提の場合が多いため、多くの人にとってはあまりガウスの消去法を使うことは無いと思われます。
ですが、実は大量の連立1次方程式を解く問題は世の中に沢山あり、その代表的な例がコンピュータシミュレーションの分野となります。
有限要素法(FEM:Finite Element Method)は特に有名で、構造物を有限の要素に離散化して連立方程式を立てます。
その方程式の数は100万、1000万はざらで、とても人間が手計算で解くべきものではありません。
ガウスの消去法は機械的に(プログラム的に)連立1次方程式を計算することができるため、コンピュータシミュレーションの分野では基本の手法となっています。
手計算で解いてみよう！
Pythonプログラミングに行く前に、簡単な例題を手計算で解いてみましょう。
問題
例題として以下の4元連立1次方程式を用意しました。
\[
\left\{\begin{matrix}
x_{1}-x_{2}-2x_{3}+2x_{4}=5\\
2x_{1}-x_{2}-3x_{3}+3x_{4}=10\\
-x_{1}+3x_{2}+3x_{3}-2x_{4}=2\\
x_{1}+2x_{2}-x_{4}=-10
\end{matrix}\right.
\]
拡大係数行列は以下の\([\mathbf{Ab}]\)になります。
\[
[\mathbf{Ab}]=\begin{bmatrix}
1&-1&-2&2&5\\
2&-1&-3&3&10\\
-1&3&3&-2&2\\
1&2&0&-1&-10\\
\end{bmatrix}
\]
解法(前進消去)
前進消去の第1ステップとして、\(a_{11}\)のピボットと呼ばれる成分で、その行の全ての要素を割ります（今回は\(a_{11}\)が既に1なので特に何もしませんが…）。
次に2行目以降について、先頭列（\(a_{11}\)ピボットと同じ列）を0にするよう、\(a_{11}\)行を定数倍して引くという同値変形を行います
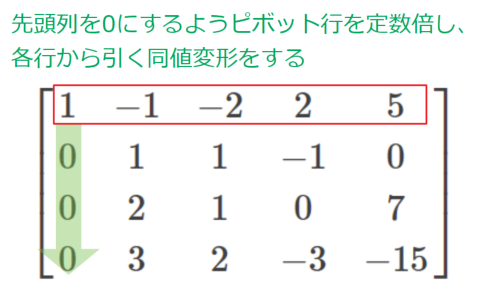
次に\(a_{22}\)をピボットとして、先ほどと同様にピボットの成分で割ります（といってもここもピボットが1なので変化はありませんが…）。
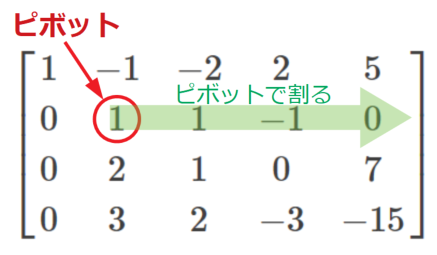
続いて3行目以降について、\(a_{22}\)ピボットと同じ列を0にするよう同値変形を行います。
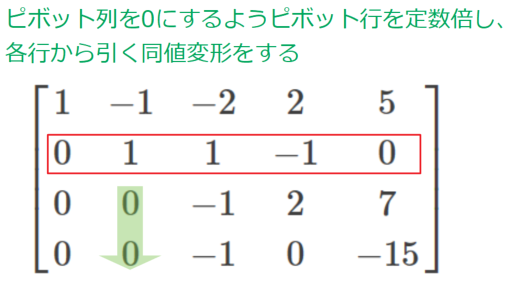
ここまで来れば「もうわかった」と言われそうですが、1つずつ説明していきます。
3行目もピボットで割り、\(a_{33}\)を1にします。
そしてピボット行の定数倍を引く同値変形を行い…
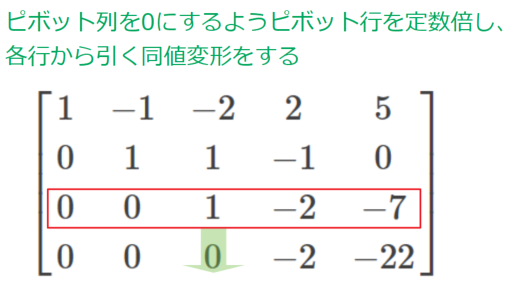
最終行の\(a_{44}\)も1にするようにピボットで割ると…係数行列の下三角が0になる階段行列を得ることが出来ました。
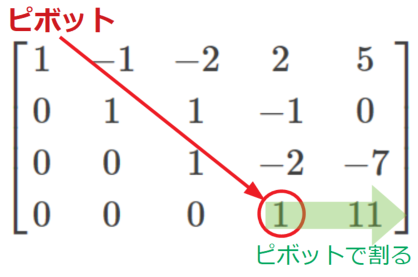
解法(後退代入)
後退代入は前進消去よりさらに簡単です。最下段は、
\[x_{4}=11\]
を意味しているので、3行目は、
\[x_{3}=-7+2x_{4}=15\]
となります。
同様に2行と1行目は、
\[x_{2}=-x_{3}+x_{4}=-4\\
x_{1}=5+x_{2}+2x_{3}-2x_{4}=9\]
と、全ての解\(x_{1}=9, x_{2}=-4, x_{3}=15, x_{4}=11\)を得ることが出来ました。
ガウスの消去法(掃き出し法)は手計算でやってみるのが最速の理解法と思います。是非手を動かしてみて下さい。
行列の基本操作があやしいという方は、以下の「技術者のための線形代数学」をオススメします。数学書にありがちな難しい言い回しはなく、数学を専門としていない人のために平易な言葉で書いてあり、入門書としては読みやすいです。
Python/Numpyによるガウスの消去法プログラム
基本コード
以下にPython3.7でコーディングしたガウスの消去法プログラムを紹介します。
詳細説明はコード内にコメントを記載しましたので、そちらを参照下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 |
import numpy as np def gaussian_elimination(A, b): n = len(b) # 前進消去を行う for i in range(n): pivot = A[i, i] # 対角成分をpivotに代入 A[i] = A[i] / pivot # pivotで係数行列を割り、A[i,i]を1にする b[i] = b[i] / pivot # 定数ベクトルもpivotで割り同値変形する # i行目の定数倍をi+1行目以降から引くループ for j in range(i+1, n): p = A[j, i] # i+1行目以降i列の数値を格納 A[j] -= p * A[i] # 係数行列のi+1行目からi行目の定数倍を引く b[j] -= p * b[i] # 定数ベクトルのi+1行目からi行目の定数倍を引く # 後退代入を行う x = np.zeros(n) # 解の入れ物を用意 for i in reversed(range(n)): # 最終行から後退処理する x[i] = b[i] / A[i, i] # 解を求める for j in range(i): b[j] -= A[j, i] * x[i] # 解が求まった列分bの値を上から更新する return x # 係数行列(n次正方行列であること) A = np.array([ [1, -1, -2, 2], [2, -1, -3, 3], [-1, 3, 3, -2], [1, 2, 0, -1]], dtype=float) # 定数ベクトル b = np.array([5, 10, 2, -10], dtype=float) # ガウスの消去法関数を実行して解を得る x = gaussian_elimination(A, b) print(x) |
実は以下の書籍「解析塾秘伝 有限要素法のつくり方」のP76にあるVBAコードを参考にしました。
書籍内ではExcel VBAで書かれていますが、Pythonだと行の割り算でforループを使わなくても良いといった違いがありましたので、Python用にいくつか変更しています。
本記事手計算の説明では拡大係数行列を作ってから計算をしていましたが、プログラム的には定数ベクトルはそのままにしておいた方が後退代入がしやすいというメリットもあるようです。
このプログラムを実行すると、すべての解がコンソールに表示されます。
|
1 |
[ 9. -4. 15. 11.] |
Pivotエラー付きガウスの消去法プログラム
先ほどのプログラムで使用していた行列は問題ありませんでしたが、pivotの値が0になってしまうことはよくあると思います。そのため、まずはエラーが発生したら正常にエラー終了させるように先ほどのコードを改修してみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 |
import numpy as np def gaussian_elimination(A, b): try: n = len(b) # 前進消去を行う for i in range(n): pivot = A[i, i] # 対角成分をpivotに代入 # pivotが小さい時はエラーとする if np.abs(pivot) < 1e-6: print('pivot=', pivot) raise ZeroDivisionError A[i] = A[i] / pivot # pivotで係数行列を割り、A[i,i]を1にする b[i] = b[i] / pivot # 定数ベクトルもpivotで割り同値変形する # i行目の定数倍をi+1行目以降から引くループ for j in range(i+1, n): p = A[j, i] # i+1行目以降i列の数値を格納 A[j] -= p * A[i] # 係数行列のi+1行目からi行目の定数倍を引く b[j] -= p * b[i] # 定数ベクトルのi+1行目からi行目の定数倍を引く # 後退代入を行う x = np.zeros(n) # 解の入れ物を用意 for i in reversed(range(n)): # 最終行から後退処理する x[i] = b[i] / A[i, i] # 解を求める for j in range(i): b[j] -= A[j, i] * x[i] # 解が求まった列分bの値を上から更新する print('Normal termination') except: print('Error termination : pivot too small.') x = np.nan return x # 係数行列(n次正方行列であること) A = np.array([ [0, -1, -2, 2], [2, -1, -3, 3], [-1, 3, 3, -2], [1, 2, 0, -1]], dtype=float) # 定数ベクトル b = np.array([5, 10, 2, -10], dtype=float) # ガウスの消去法関数を実行して解を得る x = gaussian_elimination(A, b) print(x) |
エラー処理はtryとexceptで書きました。if文でpivotの値を調べ、閾値（ここでは1e-6）未満であればraiseで強制的に0割エラー(ZeroDivisionError)フラグを立たせています。このエラーフラグが立った時点でfor文は実行されなくなり、エラー文を出力させて関数を終了させます。
以下が実行結果です。上記コードでは最初の\(a_{11}\)を0と変更しエラーとなるようにしてみました。 （「Error termination」は商用コードである某LS-DYNAをイメージしてみました。）
|
1 2 3 |
pivot= 0.0 Error termination : pivot too small. nan |
計算が正常終了すると安心の「Normal termination」文が表示されるので、是非お試し下さい。
部分ピボット選択付きガウスの消去法プログラム
先ほどの0割エラーは「部分ピボット選択」という手法を使えばほとんどの場合回避可能です。
手計算では無意識にやることだと思いますが、連立方程式なので拡大係数行列の行を入れ替える操作も同値変形となり、方程式の意味を崩しません。
以下のコードはpivotに値を格納する前に、pivot列のpivot行以降で絶対値が最大になる行を常にpivotに使うよう上記コードを改修したものになります。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 |
import numpy as np def gaussian_elimination(A, b): try: n = len(b) # 前進消去を行う for i in range(n): # pivot選択機能--------------------------------------------------------------------------------- order = np.argmax(np.abs(A[i:, i])) # pivot列i行目以上で最も絶対値の高い行を検索 temp_A = A[i + order].copy() # Aについて、最も絶対値の高い行成分を抽出し、別メモリで一時保持する temp_b = b[i + order].copy() # bについて、最も絶対値の高い行成分を抽出し、別メモリで一時保持する A[i + order] = A[i] # Aについて、一時保持した行にi行目成分を置換する A[i] = temp_A # Aについて、保持しておいた行をi行目に置換する b[i + order] = b[i] # bについて、一時保持した行にi行目成分を置換する b[i] = temp_b # bについて、保持しておいた行をi行目に置換する # ---------------------------------------------------------------------------------------------- pivot = A[i, i] # 対角成分をpivotに代入 # pivotが小さい時はエラーとする if np.abs(pivot) < 1e-6: print('pivot=', pivot) raise ZeroDivisionError A[i] = A[i] / pivot # pivotで係数行列を割り、A[i,i]を1にする b[i] = b[i] / pivot # 定数ベクトルもpivotで割り同値変形する # i行目の定数倍をi+1行目以降から引くループ for j in range(i+1, n): p = A[j, i] # i+1行目以降i列の数値を格納 A[j] -= p * A[i] # 係数行列のi+1行目からi行目の定数倍を引く b[j] -= p * b[i] # 定数ベクトルのi+1行目からi行目の定数倍を引く # 後退代入を行う x = np.zeros(n) # 解の入れ物を用意 for i in reversed(range(n)): # 最終行から後退処理する x[i] = b[i] / A[i, i] # 解を求める for j in range(i): b[j] -= A[j, i] * x[i] # 解が求まった列分bの値を上から更新する print('Normal termination') except: print('Error termination : pivot too small.') x = np.nan return x # 係数行列(n次正方行列であること) A = np.array([ [0, -1, -2, 2], [2, -1, -3, 3], [-1, 3, 3, -2], [1, 2, 0, -1]], dtype=float) # 定数ベクトル b = np.array([5, 10, 2, -10], dtype=float) # ガウスの消去法関数を実行して解を得る x = gaussian_elimination(A, b) print(x) |
今回はAとbに分けて書いているので、入れ替えはそれぞれで行う必要がありますが、これで先ほどの連立方程式もNormal terminationになりました。
（Aとbの中の行を入れ替えて検算はしてみましたが、もしお使いになる場合はご自身で検証下さい）
コード検証方法
本当に計算結果があっているのかを検証するには、最後に係数行列Aと解xの内積を計算するのが良いと思います。結果が定数ベクトルbになっていれば正解。
メイン部分のみですが、以下に検証のためのコードを示します。
本記事のプログラムはAとbの中身が計算中に変わってしまうため、検証のためにはnp.copy()で値を保持しておく必要があります。
また、このコードではデータ型を「dtype=float」としています。これをつけ忘れると値が変わってしまうのでご注意（関数の中で処理すれば良いかも？）。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 |
# 係数行列(n次正方行列であること) A = np.array([ [0, -1, -2, 2], [2, -1, -3, 3], [-1, 3, 3, -2], [1, 2, 0, -1]], dtype=float) # 定数ベクトル b = np.array([5, 10, 2, -10], dtype=float) # 検証用にコピー A_temp = A.copy() b_temp = b.copy() # ガウスの消去法関数を実行して解を得る x = gaussian_elimination(A, b) print(x) print('A@x=', np.dot(A_temp, x)) print('b=', b_temp) |
上記コードを追記して実行すると、最後に内積（A@b）とbが出力されます。この値がイコールになっていればOK。
|
1 2 |
A@x= [ 5. 10. 2. -10.] b= [ 5. 10. 2. -10.] |
連立方程式を解くその他のPythonコード
「Pythonで線形代数!連立1次方程式を解く」では、逆行列を使ったり、Pythonのsolveを使ったりした連立方程式の解き方も紹介していました。今回はFEMでよく使われている方法であるガウスの消去法を理解するためにNumpyで書いてみましたが、ご興味があればこちらの記事もご覧ください。
まとめ
本記事ではガウスの消去法（畳み込み法）の概要として、前進消去と後退代入を説明しました。そして実際に簡単な問題を手計算でステップを追いながらアルゴリズムを体感しました。
最後に、PythonのNumpyのみでガウスの消去法コードを書き、プログラム的に連立1次方程式を解く方法を紹介しました。プログラムは基本コードに加え、ピボットエラー検出コード、部分ピボット選択付きコードと計3例作ってみました。
補足
連立方程式と解について
1つ補足します。連立1次方程式の解の個数は係数行列\(\mathbf{A}\)と定数ベクトル\(\mathbf{b}\)の状態によって変わります。
以下は直線の方程式の場合の図ですが、\(\mathbf{A}\)が正則行列であれば2直線の交点というただ1つの解が存在することになります。
また、以下のように2直線が平行である場合は\(\mathbf{A}\)が正則行列にならず、定数ベクトル\(\mathbf{b}\)によって解の個数が変わります。
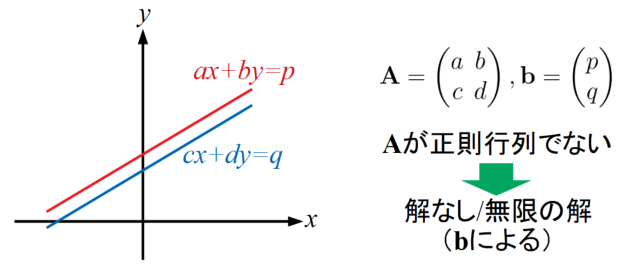
直線が離れている場合は交点が無いので解無しとなります。一方、直線が一致している場合は全ての点が解となり、無限に解が存在することを意味します。
もし今回のプログラムでエラーばかり出てしまった場合は、係数行列が正則かどうかを調べることをオススメします。
数値計算の基礎中の基礎、ガウスの消去法をプログラミングしてみました！今後は関連記事を増やす予定です！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！