
勾配降下法(最急降下法)は式がシンプルで扱いやすい最適化手法です。ここでは勾配降下法を機械学習の回帰分析に適用するための式変形方法や、Pythonで実装するためのコードを紹介します。
こんにちは。wat(@watlablog)です。今回は最近覚えた勾配降下法を実際のデータセットに対して回帰問題を解くために使ってみます!
勾配降下法を回帰問題に適用するために必要な知識
勾配降下法の概要
勾配降下法(GD:Gradient Descent)とは、勾配情報から任意関数の最小値を求める問題に使われる手法です。
勾配降下法の概要は「Pythonで1変数と2変数関数の勾配降下法を実装してみた」という記事で1変数の式から始め、2変数、多変数と説明していますので、まだご覧になっていない方は是非参照下さい。
勾配降下法の式を式(1)に示します。先ほど紹介した記事に各変数の意味を説明していますが、勾配情報と逆のベクトルで現在の値から次の値を決めて行くというシンプルなアルゴリズムです。
そして学習率\(\eta\)というハイパーパラメータを使って値更新の度合いを調整します。
$$\mathbf{x}_{i+1}=\mathbf{x}_{i}-\eta \nabla f (1)$$
様々な改良版の式もありますが、今回は基本の式(1)を使って回帰問題に適用していきます。
回帰分析で使うコスト関数
回帰分析とは、実験や計算で求めたデータ点に対し回帰モデルのパラメータを調整し、主に予測に使うカーブフィット手法です。
勾配降下法を回帰分析へ適用するためには、コスト関数(誤差関数、損失関数とも呼ばれる)を設定する必要があります。コスト関数とは、正解データ(教師データ)とモデルの誤差を比較し、モデルと良くフィットしている場合に値が小さくなるような関数です。
このような関数を定義することができれば、最小値を探査する最適化問題として扱うことができます。
今回は最も簡単な直線の式(2)を回帰モデルとして説明していきます。
$$y=w_{0}+w_{1}x (2)$$
式(2)で調整すべきパラメータは直線の切片である\(w_{0}\)と傾き(勾配)を意味する\(w_{1}\)です。
回帰問題の場合のコスト関数\(C\)として、今回は式(3)の二乗誤差関数を使用します(他にも種類があります)。
$$C=\frac{1}{2}\sum_{i=1}^{n}\left \{ y_{i} - (w_{0}+w_{1}x_{i}) \right \}^{2} (3)$$
この関数は正解値\(y_{i}\)と回帰モデル\((w_{0}+w_{1}x_{i})\)との差を求めていますが、二乗することで符号により差が相殺されてしまうことを防いでいます。
二乗の他にも絶対値をとる絶対誤差関数もありますが、こちらの二乗誤差関数を使う方法は最小二乗法として有名です。
誤差の総和の前に\(1/2\)がありますが、これは後に微分した時に1になるように便宜上付けているだけです(勾配降下法は最小値さえ求めれば良いので、係数に何を入れても問題ない)。
直線の最小二乗法は「Pythonでカーブフィット!最小二乗法で直線近似する方法」に連立偏微分方程式の結果を0にして厳密に求める方法をNumpyコード付きで書きましたので、こちらも参考にして頂ければと思います(紹介記事は微分の連鎖率のメリットを使っていませんが…)。
次はこのコスト関数を勾配降下法にかけられる形にしていきます。
微分の連鎖率(チェーンルール)
式(3)のコスト関数を勾配降下法にかけるためには、勾配情報が必要です。
今回の式は\(w_{0}\)と\(w_{1}\)が設計パラメータなので、2変数関数となります。
「Pythonで1変数と2変数関数の勾配降下法を実装してみた」では、2変数関数の場合は偏微分が必要ということを説明しました。
式(3)を\(w_{0}\)や\(w_{1}\)で偏微分するには、式を展開してからやっても良いのですが、それではスマートではありません。
効率良く微分するために、微分の連鎖率(チェーンルール)を利用します。
微分の連鎖率とは、合成関数の微分公式として覚えている方も多いと思います。
例として\(y\)を\(x\)で微分する場合、\(y\)が\(u\)の関数で、かつ\(u\)が\(x\)の関数であれば式(4)が成立します。
$$\frac{\mathrm{d} y}{\mathrm{d} x}=\frac{\mathrm{d} y}{\mathrm{d} u}\frac{\mathrm{d} u}{\mathrm{d} x} (4)$$
これはdy,du,dxを通常の分数と同じに約分しても良い(二乗等してなければ)ということを意味しており、これにより複雑な関数の微分が楽になります。
このチェーンルールは今回のコスト関数ような多変数関数の場合でも成立します。多変数になると偏微分形になるのはこれまでの勾配降下法の式の流れと全く同じです。
それでは、今回のコスト関数を\(w_{0}\)と\(w_{1}\)で偏微分してみましょう。
尚、先ほどのチェーンルールと対応させるために式(5)と\(u\)を一回挟んでみます。
$$u=y_{i}-(w_{0}+w_{1}x_{i}) (5)$$
コスト関数の偏微分結果を式(6)、式(7)に示します。
\begin{eqnarray}
\frac{\partial C}{\partial w_{0}} &=& \frac{\partial C}{\partial u}\frac{\partial u}{\partial w_{0}} \\
&=& -\sum_{i=1}^{n} \left \{ y_{i} -(w_{0}+w_{1}x_{i})\right \} (6)
\end{eqnarray}
\]
\begin{eqnarray}
\frac{\partial C}{\partial w_{1}} &=& \frac{\partial C}{\partial u}\frac{\partial u}{\partial w_{1}} \\
&=& -\sum_{i=1}^{n} \left \{ y_{i} -(w_{0}+w_{1}x_{i})\right \}x_{i} (7)
\end{eqnarray}
\]
この辺の数学的な話をさらに詳細に知りたい方は、こちらの「ディープラーニングがわかる数学入門」という本がオススメです。丁寧な式の導出がされているので、僕のような数学が苦手な人でも無理なく読むことができると思います。
ここまで導出できれば、回帰分析へ勾配降下法を適用する準備は完了です。早速Pythonコードを書いてみましょう。
勾配降下法を回帰分析に適用するPythonコード
全コード
以下に勾配降下法を回帰分析に適用するための実装コードを示します。
…とは言っても、前回の「Pythonで1変数と2変数関数の勾配降下法を実装してみた」とほとんど同じ(コスト関数とその偏微分関数が異なるくらい)書き方なので、上式の導出さえ理解できていれば問題無くコーディングできると思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 |
import numpy as np from matplotlib import pyplot as plt # 回帰モデル def reg(x, w0, w1): y = w0 + w1 * x return y # コスト関数(二乗誤差関数) def cost(x, y, w0, w1): c = (1/2) * np.sum((y - (reg(x, w0, w1))) ** 2) return c # コスト関数の偏微分 def pertial_cost(x, y, w0, w1): dcdw0 = - np.sum((y - reg(x, w0, w1))) dcdw1 = - np.sum((y - reg(x, w0, w1)) * x) dc = np.array([dcdw0, dcdw1]) return dc # サンプルデータ x = np.random.uniform(0, 10, 100) y = np.random.uniform(0.2, 1.9, 100) + x # 勾配降下法のパラメータ eta = 0.0005 # 学習率 max_iteration = 1000 # 最大反復回数 w0 = 10 # w0初期値 w1 = 100 # w1初期値 c = np.zeros(max_iteration) # コスト配列初期化 # 最大反復回数まで計算する for i in range(max_iteration): w0, w1 = np.array([w0, w1]) - eta * pertial_cost(x, y, w0, w1) # 更新式 c[i] = cost(x, y, w0, w1) # コスト算出 # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax2.set_xlabel('iteration') ax2.set_ylabel('C') # スケール設定 ax2.set_ylim(0, 100) # データプロットの準備。 ax1.scatter(x, y) ax1.plot(x, reg(x, w0, w1), color='red') ax2.plot(np.arange(0, max_iteration, 1), c) # グラフを表示する。 fig.tight_layout() plt.show() plt.close() # ------------------------------------------------------------------- |
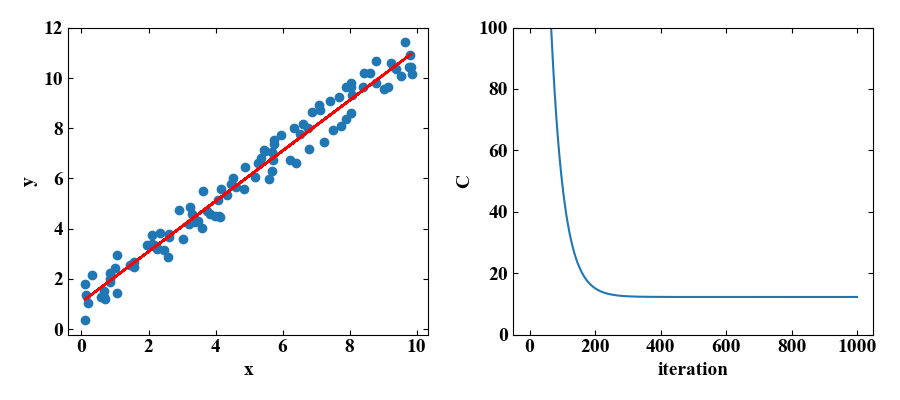
実行結果
以下が実行結果です。回帰結果の横にコスト関数の算出値を載せましたが、1000回のiterationは必要なかったかも知れません。
おまけ:反復計算中の挙動可視化コード
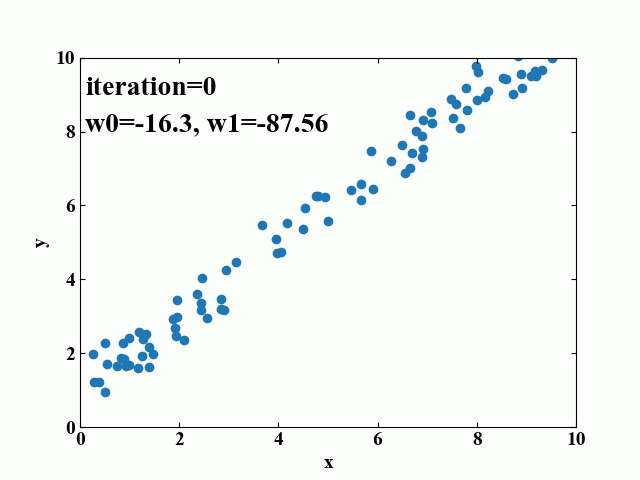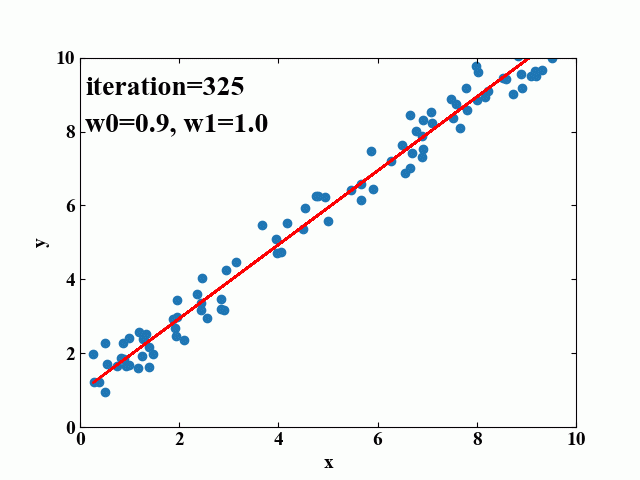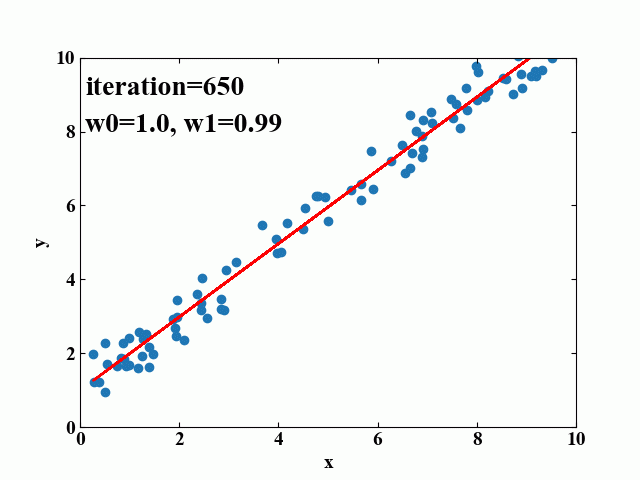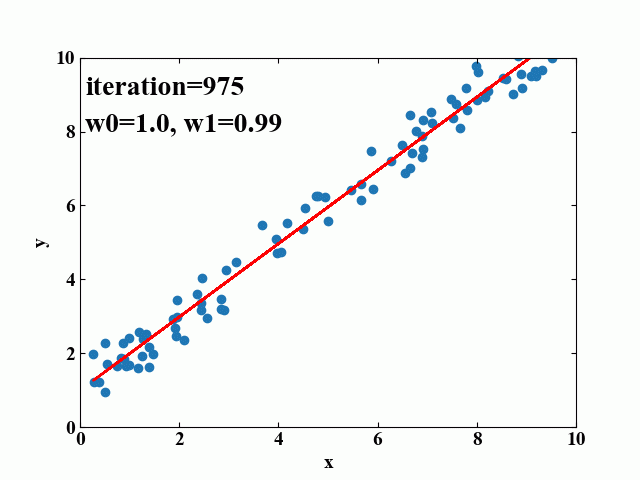
以下はおまけです。先ほどの勾配降下中のモデルを25フレーム毎に画像に保存し、GIF動画を作成してみました。このように可視化するとどういった挙動でフィットされているのかが一目瞭然となるため、理解の助けになると考えられます。
自分自身の備忘録もかね、以下に画像生成用の全コードを載せておきます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 |
import numpy as np from matplotlib import pyplot as plt # 回帰モデル def reg(x, w0, w1): y = w0 + w1 * x return y # コスト関数(二乗誤差関数) def cost(x, y, w0, w1): c = (1/2) * np.sum((y - (reg(x, w0, w1))) ** 2) return c # コスト関数の偏微分 def pertial_cost(x, y, w0, w1): dcdw0 = - np.sum((y - reg(x, w0, w1))) dcdw1 = - np.sum((y - reg(x, w0, w1)) * x) dc = np.array([dcdw0, dcdw1]) return dc # サンプルデータ x = np.random.uniform(0, 10, 100) y = np.random.uniform(0.2, 1.9, 100) + x # 勾配降下法のパラメータ eta = 0.0005 # 学習率 max_iteration = 1000 # 最大反復回数 w0 = 10 # w0初期値 w1 = 100 # w1初期値 c = np.zeros(max_iteration) # コスト配列初期化 # 最大反復回数まで計算する for i in range(max_iteration): w0, w1 = np.array([w0, w1]) - eta * pertial_cost(x, y, w0, w1) # 更新式 c[i] = cost(x, y, w0, w1) # コスト算出 print(i) if i % 25 == 0 or i == 0: # ここからグラフ設定------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # スケール設定 ax1.set_xlim(0, 10) ax1.set_ylim(0, 10) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # ------------------------------------------------------------------- path = str("{:05}".format(i)) + '.png' ax1.scatter(x, y) ax1.plot(x, reg(x, w0, w1), color='red') plt.text(0.1, 9.0, 'iteration=' + str(i), fontsize=20) plt.text(0.1, 8.0, 'w0=' + str(np.round(w0,1)) + ', w1=' + str(np.round(w1,2)), fontsize=20) plt.savefig(path) |
まとめ
前回学んだ勾配降下法の基礎知識を使って回帰モデルへ適用してみました。
勾配降下法は機械学習のコスト関数への適用がしやすいシンプルなアルゴリズムであることがわかりました。
使う上では偏微分に関する若干の知識が必要ですが、今回の内容はそれほど難しくはありません。
今後ディープラーニングを学ぶ上ではバックプロパゲーションといった知識も必要になりますが、本記事の内容でも日常の様々な最適化問題へ勾配降下法を適用することはできそうです。
徐々に役立ちそうなスキルとなってきたような気がします!最適化問題へのアプローチは奥が深いので、これからも継続して学習していきます!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!

コメント