ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました！
信号処理はノイズと切っても切れない縁があります。様々なモデル同定やテストに意思入れの無い信号としてノイズを用いることがあります。ノイズを用いる際は「どんな」ノイズか素性を知っておく必要があります。
こんにちは。wat(＠watlablog)です。
ノイズは何も邪魔な存在だけではありません。
ここでは信号処理分野では代表的なガウシアンノイズの生成とその特徴を説明します！
信号処理として必要とされるノイズ
ノイズとは？
信号処理分野で言うノイズとは、計測した信号以外の不要な雑音を意味しており、世間で頻繁に行われている「ノイズ除去」に代表されるようにできるだけ無い方が良いものとされています。
ノイズを作り出す理由とは？
本来ノイズとは邪魔な存在であり、除去する対象でもあるわけですが、本ページではあえてそのノイズを作り出そうとしています。
ノイズが必要が理由は様々ありますが、素性の確かなノイズは工学的にとても有用であることが、ノイズをあえて作り出す1つの理由です。
工学の世界ではノイズを用いて対象となるモデルの特性を得る実験や解析がよく行われています。
代表的な物に、構造物の共振調査があります。簡単に説明すると、あるモデル（実際の構造物、もしくは計算モデル）の任意の点を加振し、ある点の応答を振動として計測する実験です。
この計測したデータと入力した加振力の比をとることで、構造物の固有振動数やどんな形で動いているかといった振動特性を知ることができます。
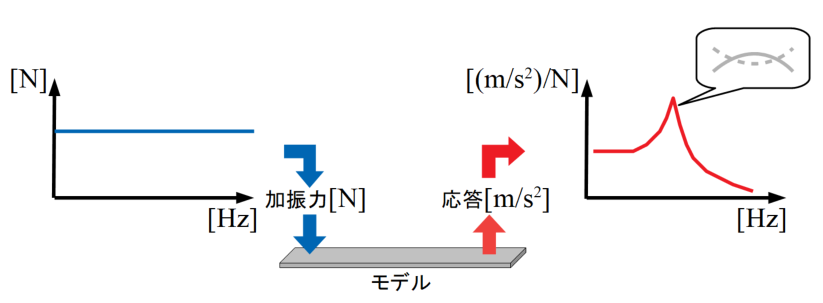
ここで、加振力は調査したい周波数帯域までできるだけクセを持たずに、フラットな特性を持つことが望ましいとされています。
適当に手で揺らせば良いわけじゃないんだね。
じゃあある程度こちらで意図したノイズを用意すれば良さそうだ。
ガウシアンノイズを作ろう！
ガウシアンノイズとは？
このページでは数あるノイズの中で、一般的に扱いが容易なガウシアンノイズを作る方法を学びます。
ガウシアンノイズとは、信号のデータ点が正規分布（ガウス分布）を持つノイズのことを指します。
ガウシアンノイズのパラメータ
正規分布を持つノイズは一つでは無く、「平均値」と「標準偏差」というパラメータで調整可能です。
以下に平均=0, 標準偏差\(\sigma\)=1の標準正規分布の例を示します。
正規分布は以下のコードで簡単に書くことができます。
|
1 2 3 4 5 6 |
import numpy as np from matplotlib import pyplot as plt from scipy.stats import norm x = np.arange(-10,10,0.01) y = norm.pdf(x,0,1) |
こちらは参考までにグラフ設定です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 |
# ここからグラフ描画 # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' fig = plt.figure() ax1 = plt.subplot(111) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Random variable') ax1.set_ylabel('Probability density') # データの範囲と刻み目盛を明示する。 plt.xticks([-4,-3,-2,-1,0,1,2,3,4], [ "","$-3\sigma$","$-2\sigma$","$-\sigma$","$0$","$\sigma$","$2\sigma$","$3\sigma$",""]) ax1.set_yticks(np.arange(0, 1, 0.1)) ax1.set_xlim(-4, 4) ax1.set_ylim(0, 0.5) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(x, y, label='PDF', lw=1) fig.tight_layout() # グラフを表示する。 plt.show() plt.close() |
ガウシアンノイズ生成のコード
ガウシアンノイズは以下のコードで生成することができます。平均値loc, 標準偏差scaleでパラメータ設定します。データのサイズsizeでガウシアンノイズを作る時間範囲を決めます。
|
1 2 |
x = np.arange(0, 12800) / samplerate # 波形生成のための間軸の作成 data = np.random.normal(loc=0, scale=1, size=len(x)) #ガウシアンノイズを生成 |
ヒストグラムとFFTで確認！
生成したノイズ信号が意図したものになっているか、信号処理をして確かめてみましょう！
尚、FFTの方法に関しては以下の記事をご覧下さい。
標準偏差\(\sigma\)を振ってみる
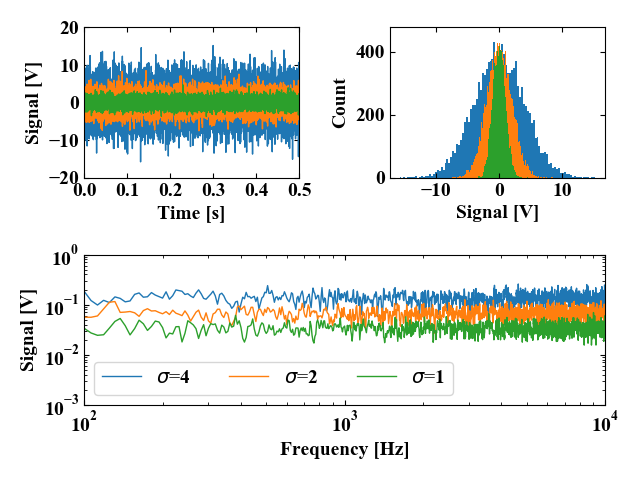
パラメータの一つである標準偏差を3段階に振った結果を以下の図に示します。
若干ヒストグラムがいびつな形をしていますが、FFT結果から周波数特性はほぼフラットになっていることがわかります。
※周波数波形で「完全に」フラットな波形にするためには、ディラックのデルタ関数を実現させるか、サイン波を周波数スイープさせるかしかないかも。
平均を振ってみる
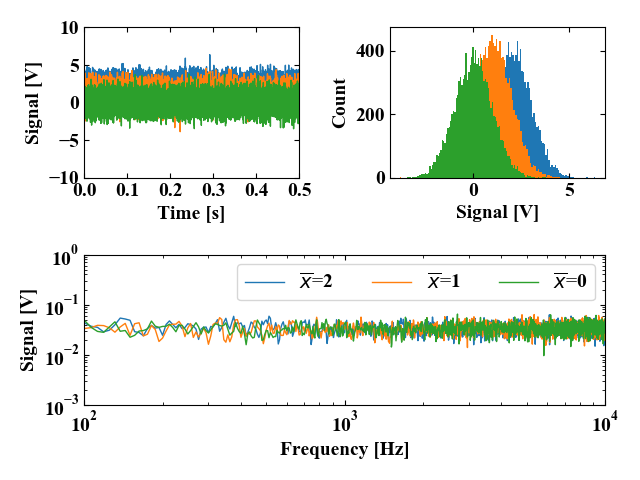
続いて、平均を振ってみた結果を以下の図に示します。
今度はヒストグラムの山がずれていきましたね。
まとめ
本ページでは、本来邪魔な存在であるはずのノイズにも、工学的に利用価値があることを説明しました。
また、ガウシアンノイズの概要と、その生成方法を示し、パラメータによる波形変化を観察しました。
これでまた1つ信号処理としての武器を得たぞ！ノイズの世界は本当はもっと奥が深そうだけど、これでまずは道具として使えるようになったかな！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！
コメント