
ロジスティック回帰は回帰と名前が付いていますが、機械学習では分類問題に使われます。ここでは、現象の発生確率を検討できることが特徴であるロジスティック回帰の概要とPython/scikit-learnによるコーディング習得を目標とします。
こんにちは。wat(@watlablog)です。今回も機械学習シリーズ!ロジスティック回帰の概要とPythonによるコーディングを学んだ結果をまとめます!
ロジスティック回帰の概要
ロジスティック回帰とは?
ロジスティック回帰(Logistic Regression)とは、線形回帰分析を分類問題に応用したアルゴリズムです。
ロジスティック回帰は病気の発生予測や商品の購買予測等、確率を検討する場合によく使われます。
下図はある特徴量\(x\)を横軸にとった時に事象の発生有無(商品を買うか否か、生存するか否か…等)をサンプリングしたデータを示しています。このような問題を回帰分析する場合を考えます。
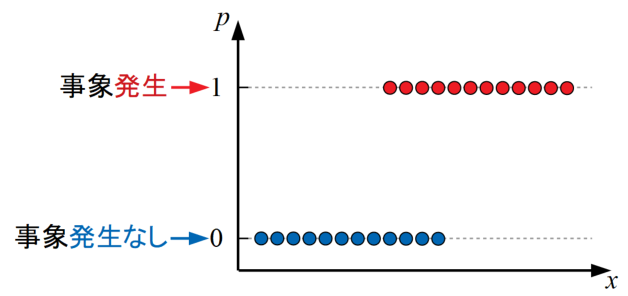
回帰問題といえば、当WATLABブログでは「Python機械学習!scikit-learnによる重回帰分析」で重回帰問題を扱いましたが、このような線形回帰手法を確率問題に適用した場合どうなるでしょうか?
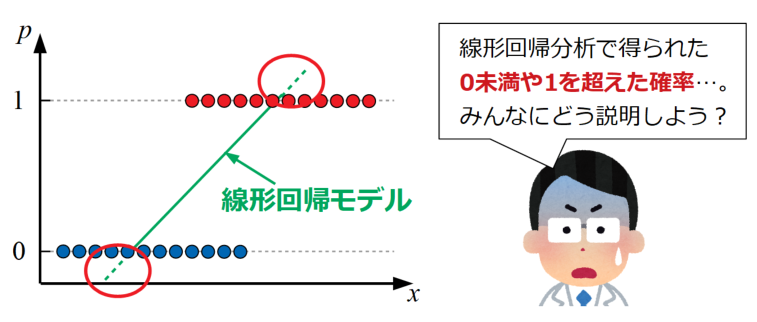
上図は線形回帰分析で得られた直線(平面や超平面の場合もある)を示していますが、線形回帰分析は0未満や1を超えた値も取り得ます。
本来確率\(p\)は0≦\(p\)≦1の範囲以外は取らないため、このままでは扱い難いモデルとなってしまいます。
シグモイド関数を使って確率を予測する
そこで考案されたのがロジスティック回帰で、この回帰分析は線形回帰の考え方を踏襲しながら、シグモイド関数を使ってモデルを0~1の範囲に収める回帰を行います。
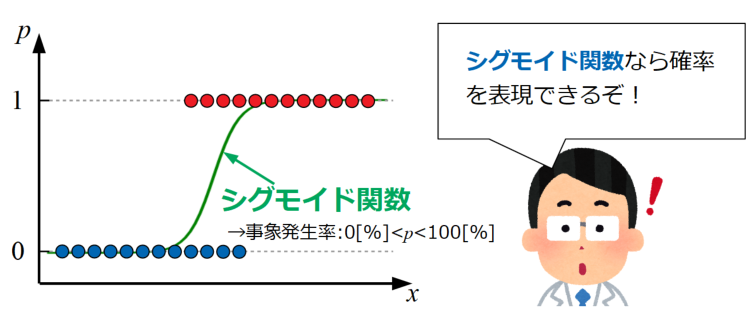
上図のシグモイド関数は式(1)で表します。この関数はディープラーニングの活性化関数でも使われており、関数自体が0~1の値をとることは「ディープラーニングにおける活性化関数をPythonで作る!」で紹介した通りです。
\[
y=\frac{1}{1+e^{-x}} (1)
\]
このシグモイド関数を使って回帰をすることができれば、病気の発生率や商品の購買確率といった2値分類問題へも応用がききそうです。
ということで、以下よりロジスティック回帰の式を少し見てみましょう。
ロジスティック回帰の回帰式
線形重回帰とシグモイド関数を両方考慮した基本式を作る
まず始めに、線形の重回帰分析で使われる回帰式を式(2)に示します。
\[y=w_{0}+w_{1}x_{1}+w_{2}x_{2}+\cdots +w_{n}x_{n} (2)\]
ここで、\(w_{n}\)は偏回帰係数で、各説明変数\(x_{n}\)の重みを意味します。\(w_{0}\)は偏回帰定数で、直線で言う所の切片に相当します。
各パラメータの詳細は「Python機械学習!scikit-learnによる重回帰分析」で紹介していますので、必要に応じて確認してみて下さい。本問題も標準偏回帰係数や多重共線性(マルチコ)の考え方は同様ですので、重回帰分析の基礎はしっかり把握しておきましょう!
少し式が長いので、偏回帰係数ベクトルと説明変数ベクトルを内積の形で書いてみると式(3)となります。
\[y=w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x} (3)\]
この形式は「Python機械学習初心者用!サポートベクターマシンの概要と実装」という記事内の式(2)でも出てきましたね。機械学習の分野ではよく出てくる形式なので曖昧な方は是非こちらの記事も確認してみて下さい!
ここで、本ページの式(1)で紹介したシグモイド関数の\(x\)にこの重回帰式(3)を代入すると式(4)を得ます。
\[p=\frac{1}{1+\exp (-(w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}))} (4)\]
確率を意味する\(p\)(Possibilityより)を使って書くこの式(4)がロジスティック回帰で使われる回帰式です。
一般的にも\(e^{-x}\)の形で書くと文字が小さくなるので\(\exp(-x)\)の形で書くことが多いようです。
線形回帰可能な形に変形させる
ロジスティック回帰式を紹介しましたが、このままの形では回帰(最小二乗法や最尤法によるフィッティング)が簡単に出来ません。
重回帰式(3)であれば簡単に回帰が可能なので、重回帰式(3)になるようにシグモイド形式で書いた確率式(4)を変形させていく方針をとります。
式(3)と式(4)の関係がとれれば線形回帰をしつつ値の範囲を0~1にとる変換が自由に出来ることを意味します。
まず、式(4)の両辺を1から引く形に変形し式(5)とします。
\[1-p=\frac{\exp (-(w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}))}{1+\exp (-(w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}))} (5)\]
\(1-\frac{1}{1+x}\)
\(=\frac{1+x}{1+x}-\frac{1}{1+x}\)
\(=\frac{x}{1+x}\)
は小中学生レベルですね。
両辺の逆数をとり式(6)とします。
\[\frac{1}{1-p}=\frac{1+\exp (-(w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}))}{\exp (-(w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}))} (6)\]
ここで、ロジスティック回帰式である式(4)(\(p\))を両辺にかけると、右辺の分子である\(1+\exp (-(w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}))\)を約分することができ式(7)を得ます。
\[\frac{p}{1-p}=\frac{1}{\exp (-(w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}))} (7)\]
式(7)は式(8)と書くこともできます。
\[\frac{p}{1-p}=\exp (w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}) (8)\]
両辺の対数をとると、式(9)を得ます。この変換で重回帰式(3)を導出できました。そしてこの式(9)はロジット\(l\)と呼ばれます。
\[\log (\frac{p}{1-p})=w_{0}+\mathbf{w}^{\mathbf{T}}\mathbf{x}=l (9)\]
\(\frac{1}{e^{-x}}=e^{x}\)
や
\(\log_{e} e^{x}=x\)
は高校レベルの変換ですね!ここまでくれば重回帰分析と同様に回帰の計算をすることができます!
用語:オッズとロジット変換
式(9)まで得られたので、用語とその意味を説明していきます。
式(8)の左辺、
\[\frac{p}{1-p}\]
は、オッズと呼ばれ、ある事象が発生する確率\(p\)と発生しない確率\(1-p\)の比となっています。
式(9)で対数をとった
\[\log (\frac{p}{1-p})\]
は、対数オッズと呼ばれます。
また、出力を0から1の値に正規化し、確率としての解釈を与える変換のことをロジット変換と呼びます。
ロジスティック回帰を分類問題に応用する考え方
上記までの内容でロジスティック回帰式を線形回帰可能な形へ変換したり、確率としての解釈を与えるロジット変換の概要がわかりました。
このロジスティック回帰を使ってある事象が発生するかしないかといった2値分類問題を計算するためには、以下の手順をとります。
①オッズ(発生率)を重回帰分析による予測する。
②オッズにロジット変換を施す。
③確率からデータが属するクラスを予測する。
ロジスティック回帰のハイパーパラメータ
ロジスティック回帰もサポートベクターマシンや決定木といったその他機械学習アルゴリズムと同様に、エンジニアが事前に値を調整しておかなければ分類精度を出すことができないハイパーパラメータを持ちます。
今回はPythonのscikit-learnを使ってロジスティック回帰分析を行いますが、全ハイパーパラメータは以下の公式ページに記載されています。
各機械学習アルゴリズムでお馴染みの正則化パラメータ\(C\)等様々なパラメータがあります。
公式ページ:https://scikit-learn.org/stable/modules/generated/sklearn.linear_model.LogisticRegression.html
詳しい式展開等は専門書に任せてしまいますが、これでざっくりとしたロジスティック回帰と分類問題への応用はわかったと思います!
早速Pythonに計算させてみましょう!
Python/scikit-learnによるロジスティック回帰コード
ロジット変換で確率を評価してみる
全コード
ロジスティック回帰を理解するためには、まず始めに上で紹介した発生有無のデータセットを使って確率評価までを行った方が効率が良いと考え、以下のコードを最初に紹介します。
このコードは特徴量\(x\)を横軸に取り、class=0のサンプルが事象発生なし、class=1が事象発生ありのグループを意味したデータセットを作ってからロジスティック回帰を行うものです。
そして回帰で得られた偏回帰係数と切片を利用して確率\(p\)(つまりロジット変換)を計算しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 |
import numpy as np import pandas as pd from sklearn.linear_model import LogisticRegression from matplotlib import pyplot as plt # シグモイド関数 def sigmoid(x): y = 1 / (1 + np.exp(-x)) return y # データを用意する------------------------------------------ # ロジスティック回帰のサンプルデータセットを生成する n = 20 # クラス毎のデータ数 df = pd.DataFrame() # データフレーム初期化 for i in range(2): # データ作成ループ x = pd.Series(np.random.uniform(0 + 2 * i, 3 + 2 * i, n)) # ランダムなx値を作成 p = pd.Series(np.full(n, i)) # 確率(発生するかしないか)を0か1で表現 temp_df = pd.DataFrame(np.c_[x, p]) # クラス毎のデータフレームを作成 df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合 df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化 # プロット用分類(色分けするため) class_0 = df[df[1] == 0] # p=0データのみ抽出 class_1 = df[df[1] == 1] # p=1データのみ抽出 # ---------------------------------------------------------- # トレーニングデータを.fitで使えるフォーマットにする X = df[0].to_numpy().reshape(-1, 1) Y = df[1].to_numpy() # 正則化パラメータCを複数振ってそれぞれのモデルを生成するループ param_C = [0.1, 1, 1000] # 正則化パラメータリスト p = [0] * len(param_C) # 初期化確率pリスト for j in range(len(param_C)): clf = LogisticRegression(C=param_C[j], solver='lbfgs') # ロジスティック回帰モデルを定義 clf.fit(X, Y) # フィッティング # 学習済モデルを使って予測 x_reg = np.arange(0, 6, 0.1) # 回帰式のx軸を作成 y_reg = clf.predict(x_reg.reshape(-1, 1)) # 予測 w0 = clf.intercept_ # 偏回帰定数(切片w0) wi = clf.coef_ # 偏回帰係数ベクトル p[j] = sigmoid(w0 + wi[0] * x_reg) # 確率pを計算してリストに格納 # ここからグラフ描画---------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフオブジェクトを定義する。 fig = plt.figure() ax1 = plt.subplot(111) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('p') # データプロットする。 n = 0 for k in range(len(param_C)): ax1.plot(x_reg, p[k], label='Possibility (C=' + str(param_C[k]) + ')') ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') plt.legend() # グラフを表示する。 plt.show() plt.close() # ---------------------------------------------------------- |
Pandas形式でデータを作成してNumpy形式に変換する回りくどいことをしていますが、これは今後の実践データ分析のためにPandasに慣れるためにやっています…。
実行結果
上記コードを実行すると、以下の図を得ます。
class=0,1の各点が事象発生有無の実サンプルで、そのサンプルデータを使ってロジスティック回帰を行って得られた確率曲線がそれぞれPossibilityとしてプロットされています。
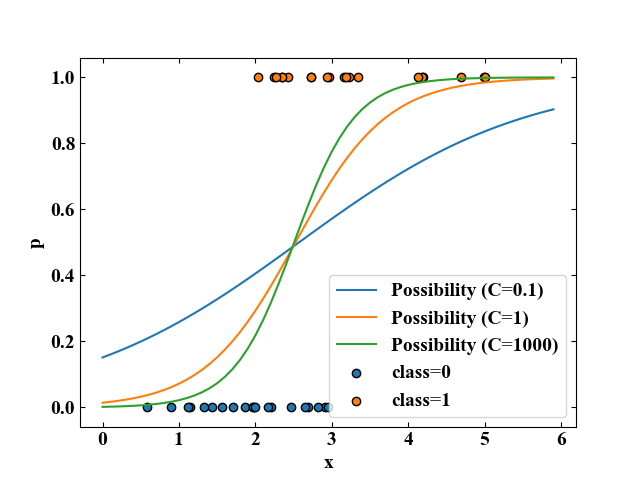
確率はロジスティック回帰のハイパーパラメータである正則化パラメータ\(C\)を振っていますが、\(C\)が大きくなるにしたがって曲率が激しくなっていく結果を得ました。
これは、\(C\)が高いとデータに過剰にフィットしやすいという過学習(オーバーフィッティング)と関係しています。
2変数2クラス分類に適用してみる
全コード
データセットを2変数に拡張したサンプルコードを以下に示します。
テストデータとしてグリッドで網羅的に見ている方法は過去のサポートベクターマシンや決定木の時と同じです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 |
import numpy as np import pandas as pd from sklearn.linear_model import LogisticRegression from matplotlib import pyplot as plt # データを用意する------------------------------------------ # 線形分離可能なデータセットを生成する n = 20 # クラス毎のデータ数 df = pd.DataFrame() # データフレーム初期化 for i in range(2): # データ作成ループ x = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなx値を計算 y = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなy値を計算 label = pd.Series(np.full(n, i)) # ラベル(クラス)を作成 temp_df = pd.DataFrame(np.c_[x, y, label]) # クラス毎のデータフレームを作成 df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合 df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化 # クラス毎のデータフレームに分離(プロット用) class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 # ---------------------------------------------------------- # 学習させる値(訓練データ)とクラス(正解ラベル)に分離 data = df[[0, 1]] # 訓練データ data_class = pd.Series(df[2]) # 正解ラベル # ロジスティック回帰による学習 clf = LogisticRegression(C=1.0, solver='lbfgs') clf.fit(data, data_class) # 決定境界可視化用 grid_line = np.arange(-5, 5, 0.05) # グリッドデータのための配列を生成 X, Y = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測 Z = Z.reshape(X.shape) # 3Dプロットするためにshapeを再変換 r2 = clf.score(data, data_class) # 決定係数を算出 # ここからグラフ描画---------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフオブジェクトを定義する。 fig = plt.figure() ax1 = plt.subplot(111) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 2) ax1.set_ylim(0, 2) # データプロットする。 ax1.contourf(X, Y, Z, cmap='coolwarm') ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') ax1.text(0.1, 1.25, '$\ R^{2}=$' + str(round(r2, 2)), fontsize=20) plt.legend() # グラフを表示する。 plt.show() plt.close() # ---------------------------------------------------------- |
実行結果
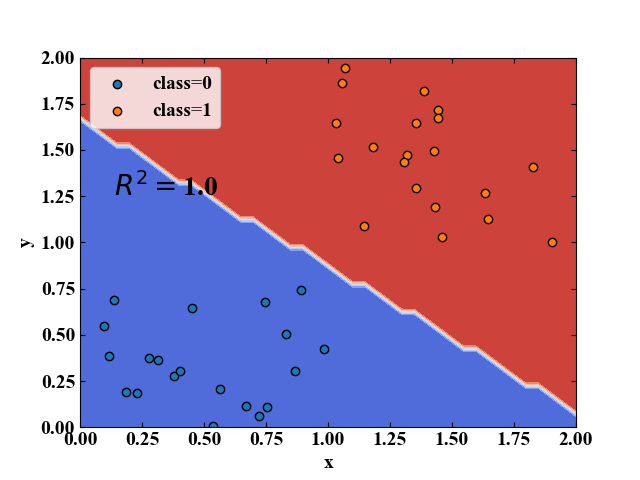
上記コードを実行すると、以下の分類結果を得ます。
決定境界を可視化しました。
分類結果と確率分布を同時プロットしてみる
全コード
最後に、2変数の場合の確率分布を同時にプロットしてみます。コードは上のものを少しいじっただけ(「#確率分布可視化用」の部分とカラーマッププロット部分)です。カラーマップの部分は以下のサイト様のコードを参考にしました。
mappable0 = ax1.pcolormesh(X,Y,z, cmap='coolwarm', norm=Normalize(vmin=-4, vmax=4)) # ここがポイント! pp = fig.colorbar(mappable0, ax=ax1, orientation="vertical")
matplotlibでカラーバーの範囲を思い通りにする
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 |
import numpy as np import pandas as pd from sklearn.linear_model import LogisticRegression from matplotlib import pyplot as plt from matplotlib.colors import Normalize # シグモイド関数 def sigmoid(x): y = 1 / (1 + np.exp(-x)) return y # データを用意する------------------------------------------ # 線形分離可能なデータセットを生成する n = 20 # クラス毎のデータ数 df = pd.DataFrame() # データフレーム初期化 for i in range(2): # データ作成ループ x = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなx値を計算 y = pd.Series(np.random.uniform(i, i + 1, n)) # ランダムなy値を計算 label = pd.Series(np.full(n, i)) # ラベル(クラス)を作成 temp_df = pd.DataFrame(np.c_[x, y, label]) # クラス毎のデータフレームを作成 df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合 df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化 # クラス毎のデータフレームに分離(プロット用) class_0 = df[df[2] == 0] # ラベル0を抽出 class_1 = df[df[2] == 1] # ラベル1を抽出 # ---------------------------------------------------------- # 学習させる値(訓練データ)とクラス(正解ラベル)に分離 data = df[[0, 1]] # 訓練データ data_class = pd.Series(df[2]) # 正解ラベル # ロジスティック回帰による学習 clf = LogisticRegression(C=1.0, solver='lbfgs') clf.fit(data, data_class) r2 = clf.score(data, data_class) # 決定係数を算出 w0 = clf.intercept_ # 偏回帰定数(切片w0) wi = clf.coef_ # 偏回帰係数ベクトル # 決定境界可視化用 grid_line = np.arange(-5, 5, 0.05) # グリッドデータのための配列を生成 X, Y = np.meshgrid(grid_line, grid_line) # グリッドを作成 Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測 Z = Z.reshape(X.shape) # 3Dプロットするためにshapeを再変換 # 確率分布可視化用 x_vector = np.c_[X.ravel(), Y.ravel()] l = [] for j in range(len(x_vector)): l = np.append(l, w0 + np.dot(wi, x_vector[j])) p = sigmoid(l) # ここからグラフ描画---------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフオブジェクトを定義する。 fig = plt.figure(figsize=(12, 4)) ax1 = plt.subplot(121) ax2 = plt.subplot(122) # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') ax2.set_xlabel('x') ax2.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 2) ax1.set_ylim(0, 2) ax2.set_xlim(0, 2) ax2.set_ylim(0, 2) # データプロットする。 map_ax1 = ax1.pcolor(X, Y, Z, cmap="coolwarm", norm=Normalize(vmin=0, vmax=1)) fig.colorbar(map_ax1, ax=ax1) ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') ax1.text(0.1, 1.25, '$\ R^{2}=$' + str(round(r2, 2)), fontsize=20) ax1.legend() map_ax2 = ax2.pcolor(X, Y, p.reshape(X.shape), cmap="gray", norm=Normalize(vmin=0, vmax=1)) fig.colorbar(map_ax2, ax=ax2) ax2.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black') ax2.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black') ax2.legend() # グラフを表示する。 plt.show() plt.close() # ---------------------------------------------------------- |
実行結果
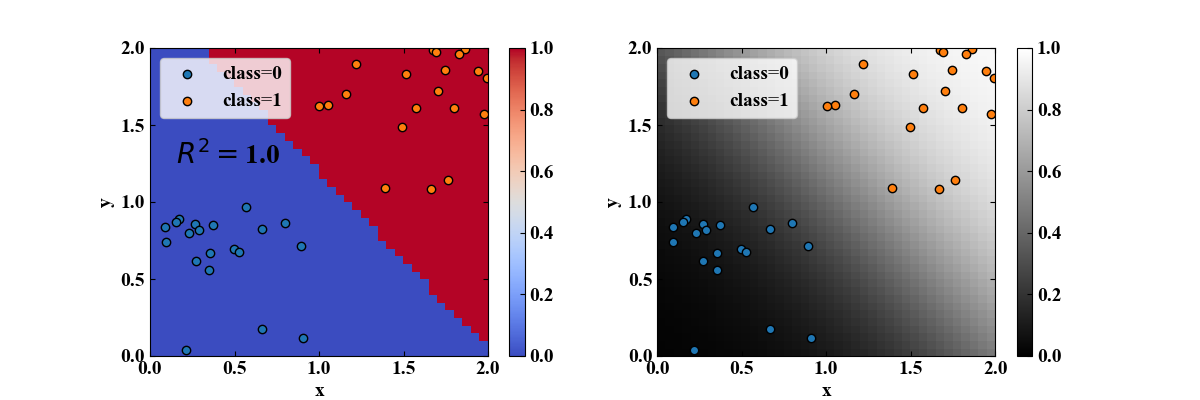
上記コードを実行すると以下の結果を得ます。
左のプロットがロジスティック回帰による分類結果で、青がclass=0、赤がclass=1を示します。
一方、右のプロットはカラーマップを回帰パラメータを使ってロジット変換した後の確率分布を示します。
シグモイド関数の曲率が斜めに入っている様子がよくわかります。
右の図が描ければ、「お前が私に勝つ確率は……50%!」とか言えるね!!
まとめ
本記事では、ロジスティック回帰分析がどういった問題に使われているか、その概要と回帰式の説明を行いました。
また、実際にデータを生成し、Python/scikit-learnによる分類や確率評価を行うコードを紹介しました。
分類はSVMとかの方がすごそうだけど、確率の検討ができるロジスティック回帰分析は使いどころを見極めれば面白い分析ができそうです!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
コメント