Python/sklearnで決定木分析!分類木の考え方とコード

決定木分析は条件分岐の繰り返しで分類や回帰を行う計算です。機械学習の中でもディープラーニングと異なり結果の解釈が容易という利点があります。ここでは決定木の中でも分類木分析の考え方概要とPython/scikit-learnによる計算方法を紹介します。

こんにちは。wat(@watlablog)です。
今回は決定木分析の一種である分類木分析の説明とPythonコードを紹介します！

決定木による分類分析の考え方

決定木とは？

決定木（Decision tree）とは、不純度が最も減少するように条件分岐を作りデータを振り分ける教師あり機械学習手法です。

不純度とは、クラス分類をする時に、一方のクラスにどれだけ他のクラスのデータが混ざっているかの度合いを示す指標で、後述するジニ係数やエントロピーといった様々な指標が存在します。

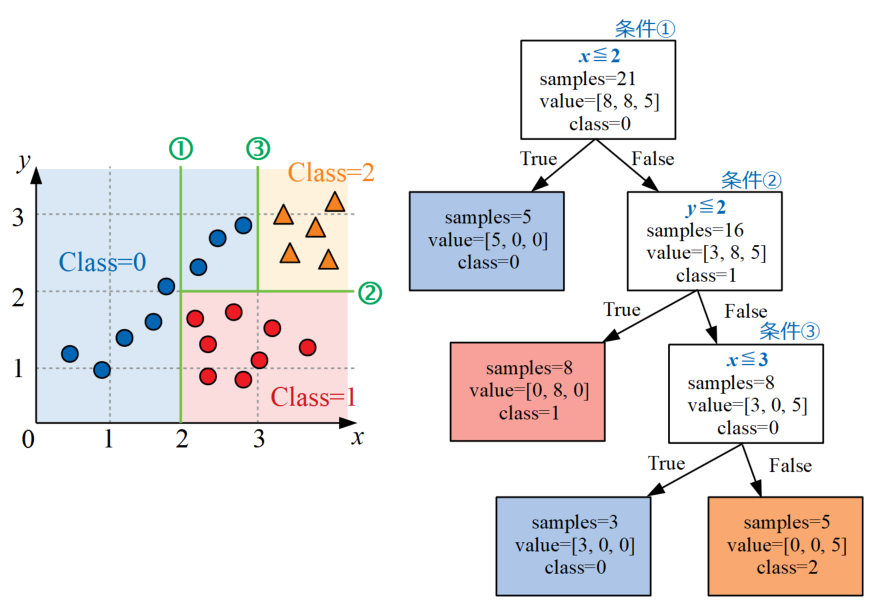
例えば以下の図のデータを決定木で書いてみます。このデータは$x$と$y$の2変数により3クラスに分類する問題の例を示しています。

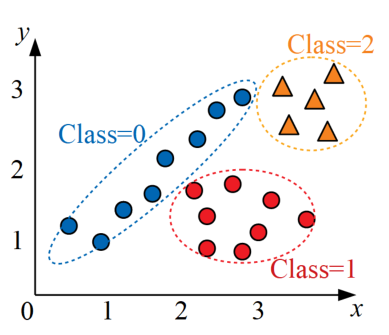
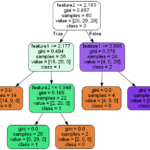
以下の図が上記データを3クラスに分類するための決定木の例です。見た目がツリー構造なので「木」というネーミングが日本語でも使われます。

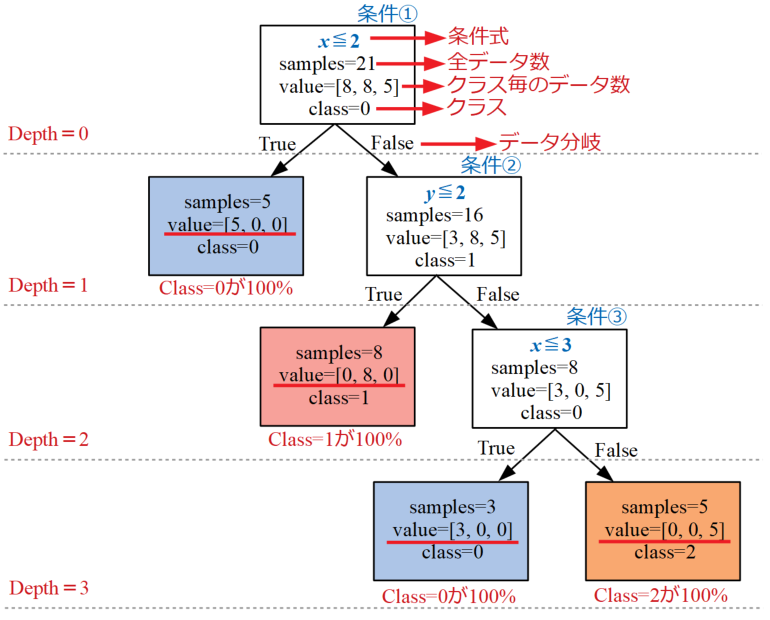
最初は中々複雑な図に見えるかも知れませんが、各階層深さ（Depth）で条件式が設定され、条件式に対してデータがTrueかFalseかを判断して振り分けていきます。

この例では各クラスが100%分類可能となるまで条件分岐を繰り返していますが、理屈上はデータの個数分条件分岐をすれば必ず全てのクラスに分類できてしまいます。

しかし、あまりにも複雑な条件分岐で決定木を構築してしまうと、それは過学習となり汎化性能を著しく落としてしまう原因となってしまいます。

汎化性能については「Python機械学習初心者用!サポートベクターマシンの概要と実装」でも説明しましたが、過学習によって汎化性能が落ちると新しいデータに対して全く役に立たない予測器が出来上がってしまうことになります。

決定木の理解は言葉よりも手を動かして覚えた方が絶対に良いです！サンプルは簡単なデータなので以下の説明をなぞって自力で条件分岐式を作ってみましょう！

手作業で決定木（分類木）を作成してみる

サンプルデータ（2変数3クラス分類問題）

データを再掲します。この2変数3クラス問題を分類する決定木、つまり分類木を作っていきます。

条件①で分岐構造を作る

データを眺めると、Class=0は$x\leq 2$の条件がTrueであれば8個のサンプルの内5個という半分以上が正確に分類可能です。

条件①として下図左のように$x=2$の位置に線を引き、ツリー構造も読み取った情報から作っていくと下図右のように作成されます。

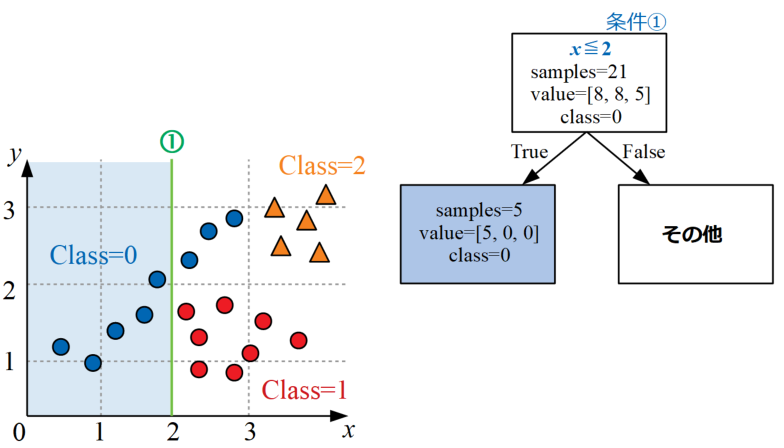
条件②で分岐構造を作る

このままだとまだClass=0の中途半端な分類しかできていないので、さらに条件分岐を重ねていきます。

次は先ほど条件①でFalseとなったデータ群に対し、条件②として$y\leq 2$という式を追加するとClass=1を全て正確に分類可能となります。

条件①の時と同様に図にすると下図の通りになります。

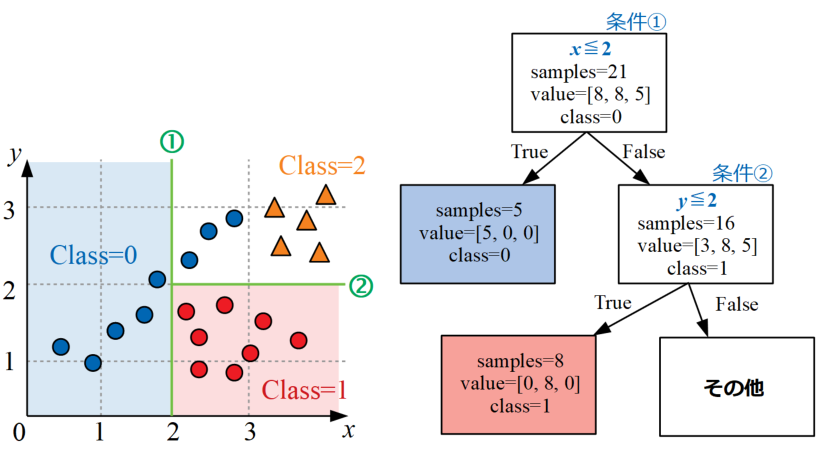
条件③で分岐構造を作る

ここで、まだ「その他」として残っている部分の条件分岐を追加します。

条件③として$x\leq 3$という式を使ってその他のデータを分類すると、Class=1の半端分とClass=2のデータ5個が正確に分類可能です。

こちらも同様に図示すると以下になります。ここまでやるとデータは完全に分類されたことになります。

決定木分析の代表的な不純度指標

ここまでは手作業で決定木を作っていきましたが、機械学習における決定木分析は自動で行われています。つまり何か決まった指標を頼りに分岐を構築していくということをしています。

その指標が不純度です。決定木では、不純度が最も小さくなるように分割をします。

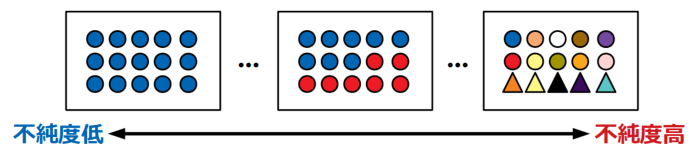
不純度は以下のイメージ図の通り、たった1つだけのクラスで分類された状態が最も低く、全て異なるクラスに分類された状態が最も高くなります。

ここでは代表的な不純度の評価指標として、ジニ係数とエントロピーという考え方を紹介します。

予備知識：ノードが持つ情報

しかし、いきなり各指標の説明に入る前に、事前知識をまとめておきましょう。

先ほど作成した決定木の中から、下図に示す任意の入れ物を持ってきました。この四角は分岐されてデータが振り分けられた入れ物ですが、名前をノードと（Node）呼びます。

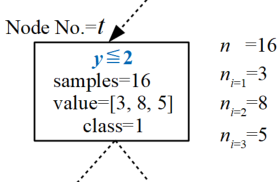
ノードは節点という意味で、FEM等の構造解析を少しやったことがある方であれば馴染みの深いものと思われますが、ここでも分岐点、節目の点という意味合いで使われています。

ここで、このノードは決定木全体では複数ありますが、$t$番目のノードには、ノード内全データサンプル数$n$、各クラスのデータサンプル数$n_{i}$（ここでは3クラス）という情報があります。

$t$番目のノードの$i$番目のクラス$C_{i}$の個数$n_{i}$の割合$p(C_{i}\mid t)$は式(1)で表現します。

\[p(C_{i}\mid t)=\frac{n_{i}}{n}　(1)\]

数学記号$\mid t$は$t$におけるという意味で馴染みの無い方は意外とこういう所で躓くかもしれませんので、ここでしっかり復習しておきましょう。

ジニ係数

まずはジニ係数(GINI Index)です。ジニ係数とは、不平等さを意味する指標で、値は0～1の範囲をとります。

$t$番目のノードのジニ係数$I_{G}$は式(2)で表現します。$m$はノード内のクラスの個数です。

\[I_{G}(t)=1-\sum_{i=1}^{m}p(C_{i}\mid t)^{2}　(2)\]

ノード内にたった1つのクラスしか存在しない時、Σの計算結果が1になるためこのジニ係数は0になります。

反対に沢山のクラスが存在する時は、それぞれの持つデータ数に応じて値が変化（沢山クラスがあるほど1に近い）します。

このように、ジニ係数は0に近いほど純粋で綺麗な分類が出来ていることを示し、1に近いほど不純であり分類できていないことを示します。

エントロピー(平均情報量)

続いてエントロピーです。ここで扱うエントロピーとは、平均情報量という意味を持ち統計分野で扱うエントロピーのことです。

$t$番目のノードのエントロピーは式(3)で表現します。

\[I_{H}(t)=-\sum_{i=1}^{m}p(C_{i}\mid t)\log p(C_{i}\mid t)　(3)\]

エントロピーも値が低いほど純度が高いことを意味し、ノード内に1つだけしかクラスが無い時が0になります。

どちらも純粋に分類できているか、不純物が混じっているかという指標であることは変わりないですね。式が違うので特性曲線が異なるのはわかるけど、今は「こんなものもあるんだ～」程度の理解です。

決定木の代表的なアルゴリズム

決定木分析は不純度を指標に条件分岐を作っていく手法ということがわかりました。実際の分析を行うアルゴリズムはいくつも考案されているので、ここでは代表的な手法のみ紹介します。

CART

CARTとは、Classification And Regression Treesの略で、分類と回帰の木という意味です。

CARTはジニ係数を不純度の指標としたアルゴリズムで、数値データの扱いに優れ、回帰問題への適用も可能な手法という特徴があります。

ID3

ID3とは、Iterative Dichotomiser 3の略で、1979年にJhon Ross Quinlanにより考案された最低限の仮説により事象を決定するというオッカムの剃刀の原理に基づいたアルゴリズムです。

このアルゴリズムではエントロピーが使われています。

C4.5/C5.0

C4.5とは、ID3の改良版で同じくQuinlanにより考案されました。ID3よりも欠損データを扱えるようになった（欠損値はエントロピー計算に使わない等）ことや、分類の役に立たないノードを剪定（リーフノードに置き換え）したりすることが大きな特徴です。

ID3を基本としているので、不純度の取扱いにはエントロピーが使われます。

C5.0はC4.0をさらに改良したアルゴリズムで、高速性やメモリの効率が向上する等様々な改良点があります。

ここでは詳細までは調べきれていませんので紹介程度ですが、余裕があったら深く調べてみたいですね。

枝の剪定

Python/scikit-learnによる分類木分析のコード

全コード

以下がPython/scikit-learnによる分類木分析の全コードです。

今回も「Python機械学習初心者用!サポートベクターマシンの概要と実装」で実施した時と同じように、サンプルデータをPandas形式で生成してから分類を行っています。

import numpy as np
import pandas as pd
from sklearn import tree
from matplotlib import pyplot as plt

# データを用意する------------------------------------------
df = pd.DataFrame()                                 # データフレーム初期化
n = 20                                              # 1クラス毎のデータ数
for i in range(3):                                  # データ作成ループ
    if i == 0:
        x = pd.Series(np.random.uniform(0.5, 2.8, n))
        y = pd.Series(x * np.random.uniform(0.8, 1.2, n))
    elif i == 1:
        x = pd.Series(np.random.uniform(2.2, 3.8, n))
        y = pd.Series(np.random.uniform(0.5, 1.8, n))
    else:
        x = pd.Series(np.random.uniform(3.2, 3.8, n))
        y = pd.Series(np.random.uniform(2.2, 3.8, n))
    label = pd.Series(np.full(n, i))                # ラベル（クラス）を作成
    temp_df = pd.DataFrame(np.c_[x, y, label])      # クラス毎のデータフレームを作成
    df = pd.concat([df, temp_df])                   # 作成されたクラス毎のデータを逐次結合
df.index = np.arange(0, len(df), 1)                 # index(行ラベル)を初期化
# クラス毎のデータフレームに分離（プロット用）
class_0 = df[df[2] == 0]                            # ラベル0を抽出
class_1 = df[df[2] == 1]                            # ラベル1を抽出
class_2 = df[df[2] == 2]                            # ラベル1を抽出
# ----------------------------------------------------------

# 学習させる値(訓練データ)とクラス(正解ラベル)に分離
data = df[[0, 1]]                                   # 訓練データ
data_class = pd.Series(df[2])                       # 正解ラベル

# 決定木による学習
clf = tree.DecisionTreeClassifier()                 # 決定木の分類木オブジェクトを定義
clf.fit(data, data_class)                           # フィッティング

# 決定境界可視化用
grid_line = np.arange(-10, 10, 0.05)                # グリッドデータのための配列を生成
X, Y = np.meshgrid(grid_line, grid_line)            # グリッドを作成
Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測
Z = Z.reshape(X.shape)                              # 3Dプロットするためにshapeを再変換
r2 = clf.score(data, data_class)                    # 決定係数を算出


# ここからグラフ描画----------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

fig = plt.figure()
ax1 = plt.subplot(111)

# グラフの上下左右に目盛線を付ける。
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_xlabel('x')
ax1.set_ylabel('y')

# スケールの設定をする。
ax1.set_xlim(0, 4)
ax1.set_ylim(0, 4)

# データプロットする。
ax1.contourf(X, Y, Z, cmap='coolwarm')
ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black')
ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black')
ax1.scatter(class_2[0], class_2[1], label='class=2', edgecolors='black')
plt.text(0.5, 2.2, '$\ R^{2}=$' + str(round(r2, 2)), fontsize=20)

plt.legend()

# グラフを表示する。
plt.show()
plt.close()
# ----------------------------------------------------------

import numpy as np

import pandas as pd

from sklearn import tree

from matplotlib import pyplot as plt

# データを用意する------------------------------------------

df = pd.DataFrame() # データフレーム初期化

n = 20 # 1クラス毎のデータ数

for i in range(3): # データ作成ループ

if i == 0:

x = pd.Series(np.random.uniform(0.5, 2.8, n))

y = pd.Series(x * np.random.uniform(0.8, 1.2, n))

elif i == 1:

x = pd.Series(np.random.uniform(2.2, 3.8, n))

y = pd.Series(np.random.uniform(0.5, 1.8, n))

else:

x = pd.Series(np.random.uniform(3.2, 3.8, n))

y = pd.Series(np.random.uniform(2.2, 3.8, n))

label = pd.Series(np.full(n, i)) # ラベル（クラス）を作成

temp_df = pd.DataFrame(np.c_[x, y, label]) # クラス毎のデータフレームを作成

df = pd.concat([df, temp_df]) # 作成されたクラス毎のデータを逐次結合

df.index = np.arange(0, len(df), 1) # index(行ラベル)を初期化

# クラス毎のデータフレームに分離（プロット用）

class_0 = df[df[2] == 0] # ラベル0を抽出

class_1 = df[df[2] == 1] # ラベル1を抽出

class_2 = df[df[2] == 2] # ラベル1を抽出

# ----------------------------------------------------------

# 学習させる値(訓練データ)とクラス(正解ラベル)に分離

data = df[[0, 1]] # 訓練データ

data_class = pd.Series(df[2]) # 正解ラベル

# 決定木による学習

clf = tree.DecisionTreeClassifier() # 決定木の分類木オブジェクトを定義

clf.fit(data, data_class) # フィッティング

# 決定境界可視化用

grid_line = np.arange(-10, 10, 0.05) # グリッドデータのための配列を生成

X, Y = np.meshgrid(grid_line, grid_line) # グリッドを作成

Z = clf.predict(np.array([X.ravel(), Y.ravel()]).T) # .predictが使えるデータshapeに変換して予測

Z = Z.reshape(X.shape) # 3Dプロットするためにshapeを再変換

r2 = clf.score(data, data_class) # 決定係数を算出

# ここからグラフ描画----------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

fig = plt.figure()

ax1 = plt.subplot(111)

# グラフの上下左右に目盛線を付ける。

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('x')

ax1.set_ylabel('y')

# スケールの設定をする。

ax1.set_xlim(0, 4)

ax1.set_ylim(0, 4)

# データプロットする。

ax1.contourf(X, Y, Z, cmap='coolwarm')

ax1.scatter(class_0[0], class_0[1], label='class=0', edgecolors='black')

ax1.scatter(class_1[0], class_1[1], label='class=1', edgecolors='black')

ax1.scatter(class_2[0], class_2[1], label='class=2', edgecolors='black')

plt.text(0.5, 2.2, '$\ R^{2}=$' + str(round(r2, 2)), fontsize=20)

plt.legend()

# グラフを表示する。

plt.show()

plt.close()

# ----------------------------------------------------------

サポートベクターマシンから決定木になったといっても、scikit-learnの構文はほとんど変更が無く、詳細説明の内容は先の記事と同じになってしまうため省きます。importで読み込むライブラリが異なり、それに従ってDecisionTreeClassifierを定義しているだけです。

実行結果

以下が実行結果です。本記事の概要説明と同じようなデータ配置にして決定木による分類を行った結果、決定境界も説明通り直線で引かれていることがわかります。

このデータではモデル精度を表す決定係数が1.0と、完璧に分類できていることを示しました（但し、ぎりぎりな点もあり、汎化性能は高くないかも）。

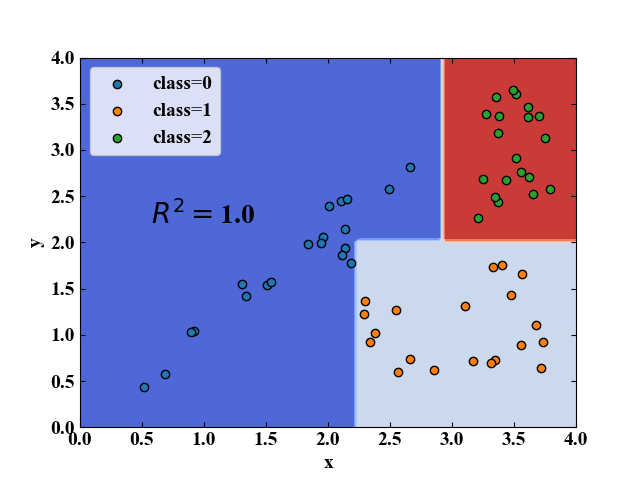
今回は簡単なデータセットによる確認であるため、ハイパーパラメータは全てデフォルトで計算しました。より複雑な分類が必要な実践データを扱う場合は別記事でまとめようと思います。

まとめ

本記事では条件分岐による機械学習である決定木の概要を紹介し、分類問題の場合に使う分類木の作り方を手作業で行うことで理解を深めました。

また、決定木を理解するのに重要な不純度や剪定の紹介を行い、実際にscikit-learnによるコードを実行し、分類性能を確かめました。

決定木は図で描くと解釈がわかりやすいですね！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

本ページで作成した決定木を可視化してみた記事を「Python決定木可視化!Graphvizの導入とdot処理方法」に書きました！是非ご覧ください。