
3Dプロットやメッシュ解析のためのライブラリ「PyVista」を使うと簡単にSTLファイルを扱うことが可能です。STLファイルはモデリングだけでなく、比較用途にも需要があります。ここでは色々なSTLファイル2面間の距離を計測してみた例を紹介します。
こんにちは。wat(@watlablog)です。この記事ではPythonを使って2つのSTLファイル間の距離計測を行ってみます!
サーフェス間の距離計測とは?
この記事で扱う「サーフェス間の距離計測」とは、下図のようにSTLファイルで作られた基準面に対し、同じくSTLファイルで作られたもう一方の面がどれだけ離れているかを可視化することです。
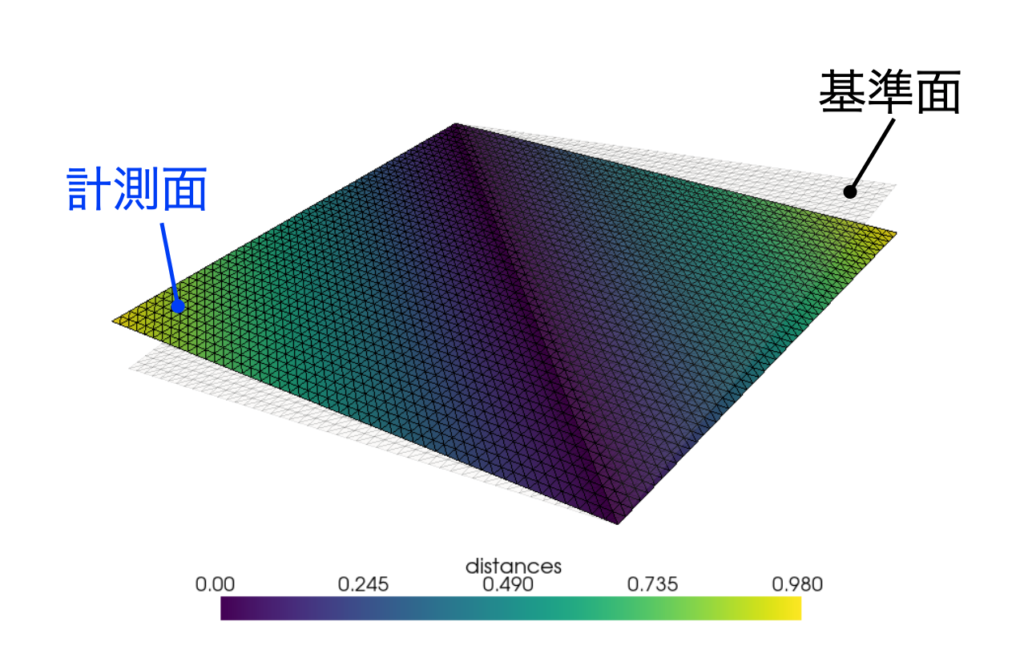
距離の計測方法には色々ありますが、ここでは最近接距離を扱います。
最近接距離とは同一頂点同士の距離でなく、最も近いと推定される面の距離を意味します。
目的によっては同一頂点(同一ノード)同士の距離が欲しくなりますが、それはそんなに難しくないのでこの記事の最後におまけとしてコードを載せようと思います。
また、距離計測は当ブログでも何度も紹介しているPyVistaというライブラリを使用します。まだ使ったことがない方は、是非以下の記事を読んでみてください。
PyVistaをインストールしてPythonでSTLを扱う備忘録
Python/PyVistaでSTLモデルを座標変換してみた
さらに、PyVistaは公式ドキュメントも豊富です。まずはこちらを読むと大体のことは解決すると思いますので、是非ご覧ください。
公式:https://pyvista.github.io/pyvista-docs-dev-ja/index.html
STLファイルのサーフェス間距離を計測したい場面
シミュレーション結果と実測結果の形状比較をしたい時
筆者は主にメカ系の開発職に従事していますが、最近の製品開発は当たり前のようにシミュレーションを活用しています。
商用ソフトはなんとなく解析条件を設定して計算をかけると、それっぽい結果を見せてくれます。
V字開発等における開発フェーズによっては机上でよく考えられた条件を使って計算を行い、計算力学的、物理的に打倒な結果であることが確かめられればそれで目的を達成できる場合もあります。
しかし詳細設計の段階で活用するシミュレーションとなると、それなりに実験結果を再現する結果を求められます(特に開発責任者や経営の立場の人から)。
そのためシミュレーション結果と実験結果をよく比較した上で、改良仕様が試作するに妥当なのかどうかといった判断が行われます。
比較は様々な視点で行いますが、製品形状に関する比較についてはやはり色々なソフトでデファクトスタンダードになっているSTLファイルを使うのが便利です。
実測結果同士を比較したい時
最近では非接触の形状測定精度が向上してきていることから、実物形状もSTLファイルで確認することがあります。
シミュレーションとの比較以外にも、実測結果同士のSTLファイルを比較するニーズも多々あります。
この記事では高価なソフトをいちいち使わなくても、気軽に使えるPythonでSTLファイルの比較ができないかな?という調査的なノリで書いています。
正直フリーソフトでも十分比較はできてしまうのですが、もしかしたらPythonで計測できると自動評価等もできるようになるかも?
動作環境
この記事では以下の環境で動作を確認しました。
PC
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| pyvista | 0.35.2 |
PyVistaでSTLファイル間の距離計測をするコード
自作のSTLファイルでチュートリアルを実行
それでは早速コードを書いていきますが、PyVistaにはわかりやすい公式チュートリアル(目的別サンプルコード)が既にあります。今回は以下のページを参考にしています。
PyVista公式:2つのサーフェス間の距離
まずチュートリアルの内容を自作のSTLで動作確認を行ってみます。
2つの平面STLファイルを用意するコード
STLファイルを2つ用意するサンプルコードを紹介します。
generate_surface()関数に平面のパラメータ(Xの係数a、Yの係数b、定数c)を与えてSTLファイルを2回作っています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 |
import pyvista as pv import numpy as np def generate_surface(filename, a, b, c): ''' サーフェス(平面)を作成してSTLファイルに保存する ''' # サーフェスデータを作成 x = np.arange(0, 10, 0.2) y = np.arange(0, 10, 0.2) X, Y = np.meshgrid(x, y) Z = a * X + b * Y + c # メッシュデータに変換 points = np.column_stack((X.ravel(), Y.ravel(), Z.ravel())) points = pv.PolyData(points) mesh = points.delaunay_2d() # 表示させて確認 #mesh.plot(show_edges=True) # STLファイルに保存 pv.save_meshio(filename, mesh) return if __name__ == '__main__': generate_surface('mesh1.stl', 0, 0, 0) generate_surface('mesh2.stl', 0.1, -0.1, 0) |
mesh1.stlとmesh2.stlが作成されます。
チュートリアルコード(.find_closest_cell)
公式の解説では色々な方法が紹介されていますが、ここでは筆者が最も簡単と思った.find_closest_cellというフィルタで計算を行うメソッドを使って距離計測します。
以下が距離計測のコードです。※今回は関数の形で書いています。
mesh1.find_closest_cellを使ってmesh1点の中でmesh2の各点と最も近い点がどこかを計算しています。
次にnp.linalg.normにより距離を計算し、mesh2に新しく距離データを追加しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 |
import pyvista as pv import numpy as np def comparison_surf(filename1, filename2): ''' 2つのサーフェス間の距離を計測する(mesh1に対するmesh2の距離を計測する) ''' # 2つのSTLファイルを読み込む mesh1 = pv.read(filename1) mesh2 = pv.read(filename2) # 近接点の計算をする closest_cells, closest_points = mesh1.find_closest_cell(mesh2.points, return_closest_point=True) # mesh1と近接点のノルム(距離)を計算 d_exact = np.linalg.norm(mesh2.points - closest_points, axis=1) # メッシュデータに新しく距離の項目を追加し、平均距離を出力 mesh2['distances'] = d_exact print('Average distance=', np.mean(d_exact)) # 可視化 pv.global_theme.font.color = 'black' p = pv.Plotter() p.add_mesh(mesh2, scalars='distances', show_edges=True) p.add_mesh(mesh1, color=True, opacity=0.1, show_edges=True) p.set_background('white') p.show() return if __name__ == '__main__': # mesh1に対するmesh2の距離を計測する comparison_surf('mesh1.stl', 'mesh2.stl') |
上記コードを実行することで、冒頭の絵で示したカラーコンター図が表示されます。色が距離を意味しています。
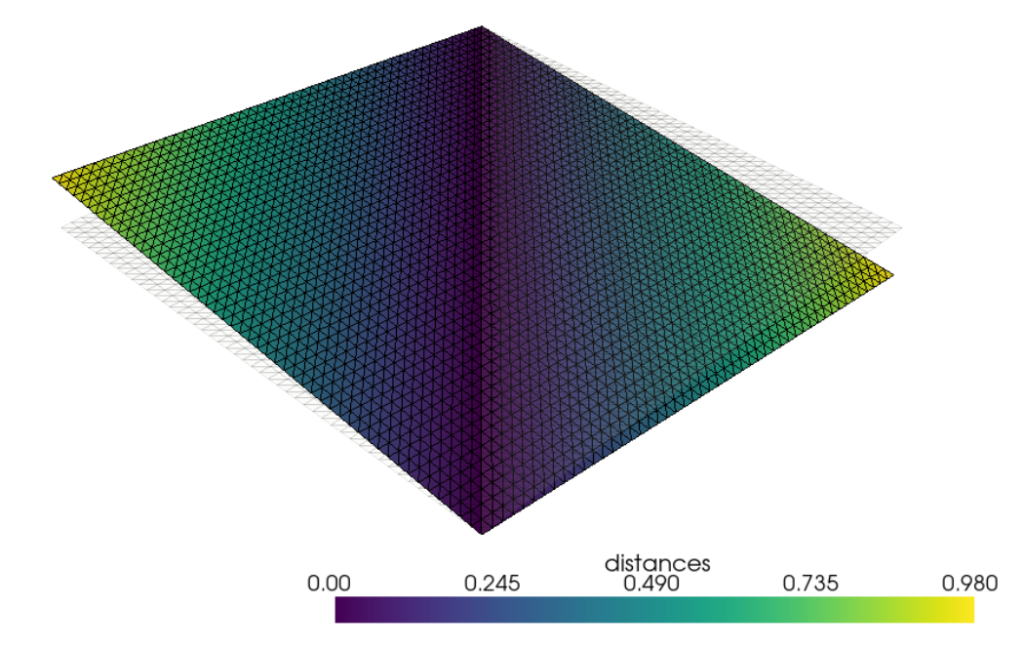
チュートリアルをそのまま書くだけで、自作のSTLでも正常に動作しました。結構簡単ですね。
STLファイルを並進移動させて距離を検証
並進移動させたファイルの作成
ちょっと平面を一定量動かして、計測された距離の数値を確認してみましょう。
STLファイルを並進移動させるコードは、「Python/PyVistaでSTLモデルを座標変換してみた」に記載しました(少し書き方は変えていますが)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import pyvista as pv import numpy as np def generate_surface(filename, a, b, c): ''' サーフェス(平面)を作成してSTLファイルに保存する ''' # サーフェスデータを作成 x = np.arange(0, 10, 0.2) y = np.arange(0, 10, 0.2) X, Y = np.meshgrid(x, y) Z = a * X + b * Y + c # メッシュデータに変換 points = np.column_stack((X.ravel(), Y.ravel(), Z.ravel())) points = pv.PolyData(points) mesh = points.delaunay_2d() # 表示させて確認 #mesh.plot(show_edges=True) # STLファイルに保存 pv.save_meshio(filename, mesh) return def translation(file_in, file_out, Tx, Ty, Tz): ''' STLファイルの並進移動をする ''' mesh = pv.read(file_in) points = mesh.points T = np.array([Tx, Ty, Tz]) for i in range(3): points[:, i] = points[:, i] + T[i] mesh.points = points pv.save_meshio(file_out, mesh) return points if __name__ == '__main__': generate_surface('mesh1.stl', 0, 0, 0) translation('mesh1.stl', 'mesh2.stl', 0, 0, 8) |
並進移動したSTLファイルの距離計測結果
先ほどの距離計測コードをそのまま使って結果を確認してみます。
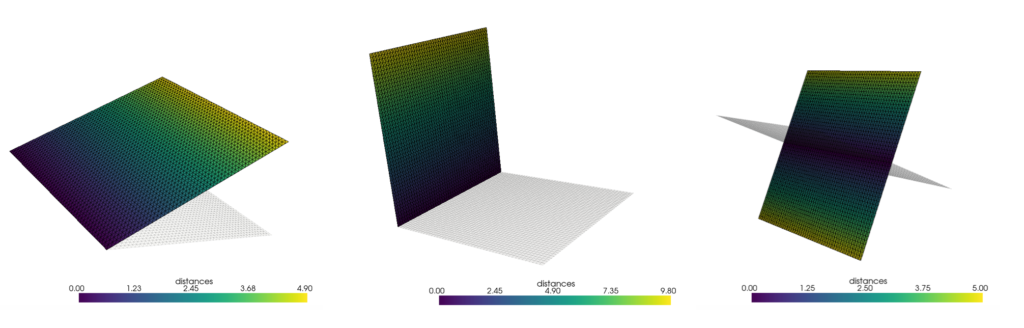
とりあえず平面の高さ値を3種類振って確認してみましたが、カラーバーの数値は意図した通りの数値を返しています。
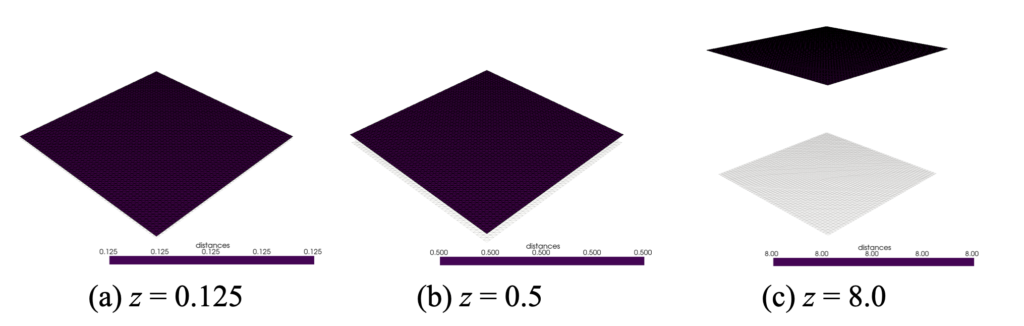
平面をせん断方向(y方向)に並進移動させてみた結果も確認してみます。
以下図はy方向を8だけ動かした結果ですが、最近接距離を計測しているので、各点が同じだけ動いたとしても分布を持つ結果となりました(しかしこれは予想通りですね)。
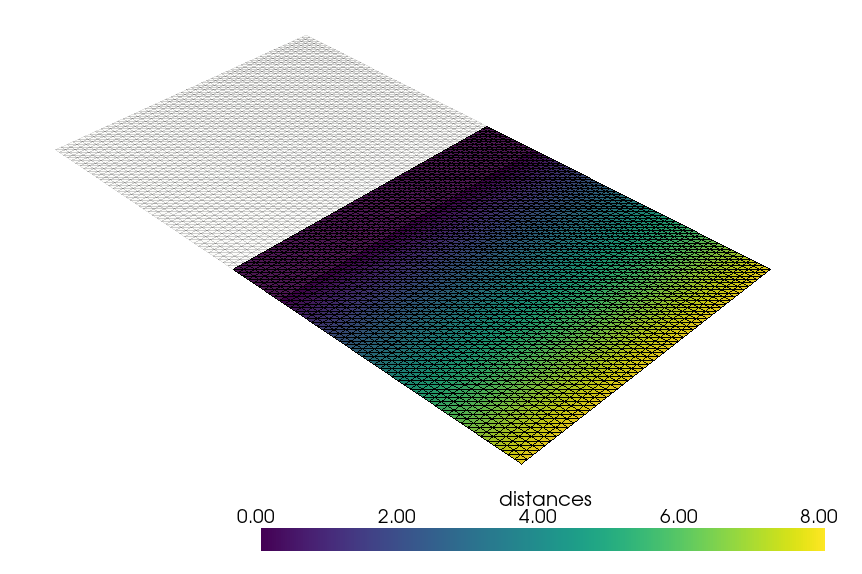
移動したという結果を表現するためには、同一ノードで距離計算をする必要があります。
STLファイルを回転移動させて距離を検証
回転移動させたファイルの作成
先ほどの検証でもう結果は読めますが、次はSTLに回転移動を施した検証をしてみましょう。
回転移動は同じく「Python/PyVistaでSTLモデルを座標変換してみた」のコードを流用します。ただ、こちらも今回の目的のためにちょっと修正しています。
一番下のmainコードで、rot関数の引数に中心座標と各軸の角度を入力することで回転移動を考慮可能です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
import pyvista as pv import numpy as np def generate_surface(filename, a, b, c): ''' サーフェス(平面)を作成してSTLファイルに保存する ''' # サーフェスデータを作成 x = np.arange(0, 10, 0.2) y = np.arange(0, 10, 0.2) X, Y = np.meshgrid(x, y) Z = a * X + b * Y + c # メッシュデータに変換 points = np.column_stack((X.ravel(), Y.ravel(), Z.ravel())) points = pv.PolyData(points) mesh = points.delaunay_2d() # 表示させて確認 #mesh.plot(show_edges=True) # STLファイルに保存 pv.save_meshio(filename, mesh) return def translation(file_in, file_out, Tx, Ty, Tz): ''' STLファイルの並進移動をする ''' mesh = pv.read(file_in) points = mesh.points T = np.array([Tx, Ty, Tz]) for i in range(3): points[:, i] = points[:, i] + T[i] mesh.points = points pv.save_meshio(file_out, mesh) return points def rot(file_in, file_out, center, theta_x, theta_y, theta_z): ''' STLファイルの回転移動をする ''' theta_x = np.radians(theta_x) theta_y = np.radians(theta_y) theta_z = np.radians(theta_z) rx = [[1, 0, 0], [0, np.cos(theta_x), -np.sin(theta_x)], [0, np.sin(theta_x), np.cos(theta_x)]] ry = [[np.cos(theta_y), 0, np.sin(theta_y)], [0, 1, 0], [-np.sin(theta_y), 0, np.cos(theta_y)]] rz = [[np.cos(theta_z), -np.sin(theta_z), 0], [np.sin(theta_z), np.cos(theta_z), 0], [0, 0, 1]] translation(file_in, file_out, -center[0], -center[1], -center[2]) mesh = pv.read(file_out) points = mesh.points for i in range(len(points)): points[i] = np.dot(rz, np.dot(ry, np.dot(rx, points[i]))) mesh.points = points pv.save_meshio(file_out, mesh) translation(file_out, file_out, center[0], center[1], center[2]) return if __name__ == '__main__': generate_surface('mesh1.stl', 0, 0, 0) rot('mesh1.stl', 'mesh2.stl', [5, 5, 0], 90, 0, 0) |
回転移動したSTLファイルの距離計測結果
こちらが結果です。…予想通り最近接距離を計測していることがわかりました。
おまけ①: 同一ノード距離を計測するコード
先ほどまでは最近接距離を計測していました。
最近接距離は実測結果と解析結果を比較する時は便利ですが、同じモデルがただ並進移動した時のようなケースはその移動量を全ノード(節点/頂点)にマッピングして可視化したいところです。
ここではおまけとして同一ノード距離を計測するコードを紹介します。
といっても実装はとても簡単です。d_exactの内容を.pointsで抽出した各点に対するL2ノルムを計算すれば良いだけです。
L2ノルムとは、ユークリッドノルムとも呼ばれるいわゆる普通の長さです(2次元平面で\(d=\sqrt{x^{2}+y^{2}}\)で計算できる長さ)。
以下に全コードを示します。np.roundは数値を切りよくしたかったから付けましたが、外しても構いません。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 |
import pyvista as pv import numpy as np def comparison_surf(filename1, filename2): ''' 2つのサーフェス間の距離を計測する(mesh1に対するmesh2の距離を計測する) ''' # 2つのSTLファイルを読み込む mesh1 = pv.read(filename1) mesh2 = pv.read(filename2) # 各メッシュの座標を成分に分割 x1 = mesh1.points.T[0] y1 = mesh1.points.T[1] z1 = mesh1.points.T[2] x2 = mesh2.points.T[0] y2 = mesh2.points.T[1] z2 = mesh2.points.T[2] # mesh1とmesh2の同一ノード距離(L2ノルム)を計算 d_exact = np.round(np.sqrt((x2 - x1) ** 2 + (y2 - y1) ** 2 + (z2 - z1) ** 2),4) # メッシュデータに新しく距離の項目を追加し、平均距離を出力 mesh2['distances'] = d_exact print('Average distance=', np.mean(d_exact)) # 可視化 pv.global_theme.font.color = 'black' p = pv.Plotter() p.add_mesh(mesh2, scalars='distances', show_edges=True) p.add_mesh(mesh1, color=True, opacity=0.1, show_edges=True) p.set_background('white') p.show() return if __name__ == '__main__': # mesh1に対するmesh2の距離を計測する comparison_surf('mesh1.stl', 'mesh2.stl') |
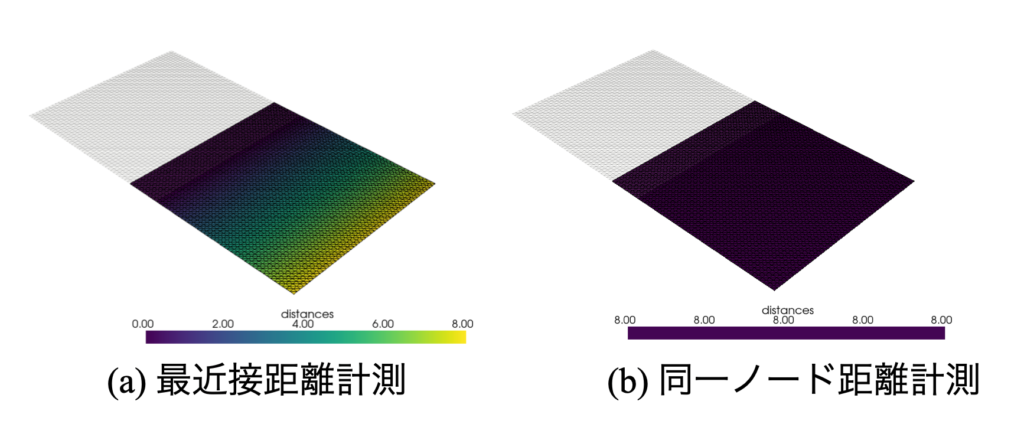
以下はSTLをせん断方向に移動させた場合のファイルで検証した例です。このように、最近接距離では分布を持っていましたが同一ノードでは全ての値が一緒になりました。移動を表現したい場合は同一ノード距離の方が適していると言えます。
おまけ②: STLファイルの各点xyz座標の可視化
距離計測に関するおまけ②は、単一STLファイルに対する座標値の可視化です。
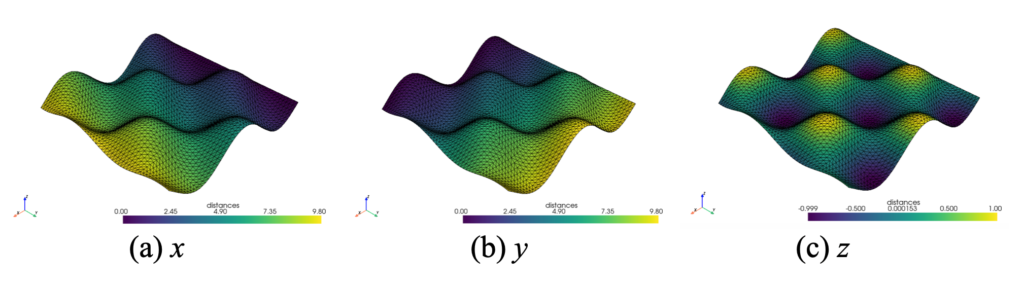
単一STLファイルの高さ方向成分の数値をコンター図で示すことにより、モデルの寸法ムラを評価可能です。
下のコードは任意のSTLファイルを指定し、各方向(x=0, y=1, z=2)の座標値をコンター図として表示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 |
import pyvista as pv import numpy as np def check_direction_coordinate(filename1, direction): ''' STLファイル任意方向の座標値をコンターで可視化する ''' # STLファイルを読み込む mesh1 = pv.read(filename1) # 指定した方向の座標を抽出 d_exact = mesh1.points.T[direction] mesh1.points = d_exact # メッシュデータに新しくデータを登録 mesh1['distances'] = d_exact print('Average distance=', np.mean(d_exact)) # 可視化 pv.global_theme.font.color = 'black' p = pv.Plotter() p.show_axes() p.add_mesh(mesh1, scalars='distances', show_edges=True) p.set_background('white') p.show() return if __name__ == '__main__': # STLファイルの任意方向(x=0, y=1, z=2)成分をコンター図で確認する check_direction_coordinate('mesh1.stl', 2) |
わかりやすいようにZ = np.sin(X) * np.cos(Y)の関数で試してみた結果を下図に示します。PyVistaはmeshオブジェクトに「mesh1['distances'] = d_exact」のようにデータを登録できるようです。
そして「scalars='distances'」でスカラー表示を行っています。
まとめ
この記事ではPyVistaというライブラリを使ってSTLファイルを扱い、2つのサーフェス間の距離を計測するPythonコード例をいくつか紹介しました。
また2つのサーフェス間を最近接距離で計測する方法以外にも、同一ノード間で計測する場合、最後に単一STLファイルの座標値を方向別に可視化する方法も実装してみました。
簡単にモデルにデータをマッピングできるので大変便利ですね。工夫次第で色々なDIYデータ処理ができそうとわかりましたので、これからも利用していこうと思います。
3DモデルをPythonで扱うのは新鮮ですね!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!