Pythonでジェフコットローターの2面アンバランス振動を計算する

　回転機の振動問題はアンバランスの修正を目的に検討される場合が多いですが、振動を毎回実験で評価するのは時間がかかって大変です。ここでは実機がなくても簡単に回転機の振動検討ができるよう、Jeffcott Rotorの問題をPythonで解析してみます。アンバランスでよく検討される2面のモデルに対応しているので、是非参考にしてください。

こんにちは。wat（@watlablog）です。ここでは回転機のシミュレーションを発展させ、2面のアンバランス振動を計算することができるジェフコットローターを扱います！

目次（項目クリックでジャンプできます）

この記事のモチベーション

2面のアンバランス振動を解析する

前回記事のおさらい

　WATLABブログでは過去に以下2つの記事で回転機の振動シミュレーションを行ってきました。

・回転機のアンバランス振動をシミュレートするPythonコード
・回転機の振動シミュレーションで回転パルスを設定してみた

　上の記事では基本的な運動方程式と、それをPythonで数値解析するコードを紹介しました。そして回転数をスイープアップさせていったときの挙動を観察し、教科書通りの挙動を得ることまで確認しました。
　下の記事では回転機の計測をするときによく使う回転パルスの表現をシミュレーションに組み込む方法を書いています（我流ですが）。こうすることで回転機の振動として重要なアンバランスの位相に着目した検討ができるようになります。
　実はこれらの記事で扱っている回転機（ローター）もジェフコットローターと呼ばれるローターを想定しています。前回までは1面の変位や速度しか見ていませんでしたが、今回はこのジェフコットローターを2面の振動計測ができるように運動方程式を拡張します。

なぜ2面で振動を確認したいか？

　回転機のアンバランス振動を分析するということは、そのアンバランス振動が実機動作中に問題にならないように修正することを目的とするのが一般的です。しかし1面だけしか振動を計測していないとほとんどのケースで満足にアンバランス修正はできません。
　例えば自動車のタイヤ交換時に行うホイールのアンバランス修正作業は回転軸方向で2箇所にカウンターウェイトをつけてバランシングをします。これは1箇所だけだと面振れの成分を除去できないからであり、このようなアンバランス修正の理解を得るために今回2面の振動を確認するというのが主なモチベーションです。

　回転機やバランスについて、わかりやすい記事があったのでこちらも参考にしてみてください。
・【ターボ機械シリーズ③】　ローターダイナミクスとは

UnbalanceとImbalanceについて

　ローターダイナミクスの分野で英語の文献を読んでいると、アンバランス（Unbalance）とインバランス（Imbalance）という表現が混在しています。どちらも「不均衡」を意味しますが、主にUnbalanceは質量の不均衡を意味し、ISO 1925:2017でも定義されています。Imbalanceの方はもっと広義の不均衡（質量分布の不均衡以外など）を意図している場合が多いとのことです。しかしImbalanceの方はISOで定義されているわけではなく、論文の著者が好みで使用することが多いそうです。この記事ではUnbalanceで統一していますが、参考までに。

2面を考慮したジェフコットローター

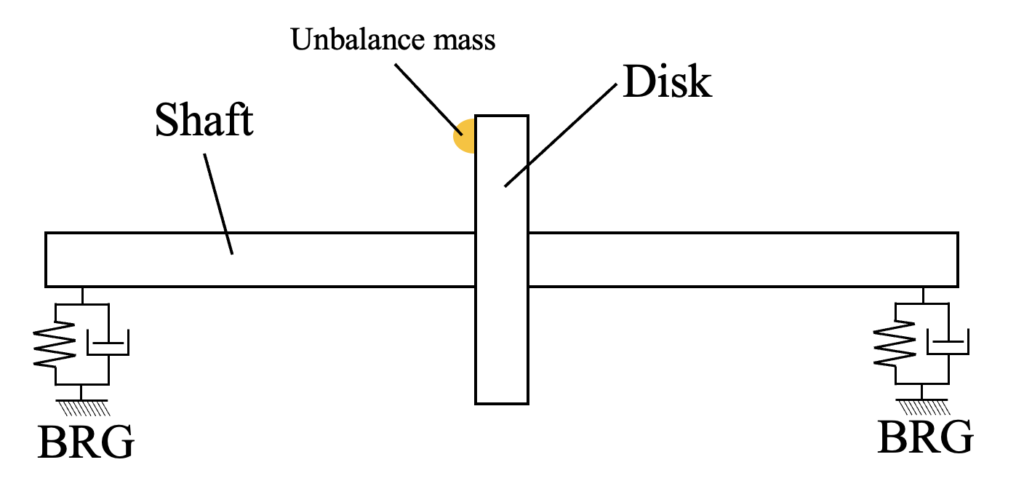
　ジェフコットローター（Jeffcott Rotor）とは、回転機の振動解析において最も単純化したモデルとしてよく使われています。先ほど紹介した記事もジェフコットローターモデルを扱っていますが、このモデルには以下の仮定があります。

ローターの質量はディスクに集中している
シャフトは線形ばねである
軸受（ベアリング：BRG）はばねとダンパーで構成される
単面のジェフコットローターは下図ですが、シャフトの質量は無視しています。そしてシャフトは線形のばね定数を持ちます。この剛性を連結剛性と呼び、本来はシャフトの長さや材料定数、断面形状で決まる剛性を簡易的に表現したものです。

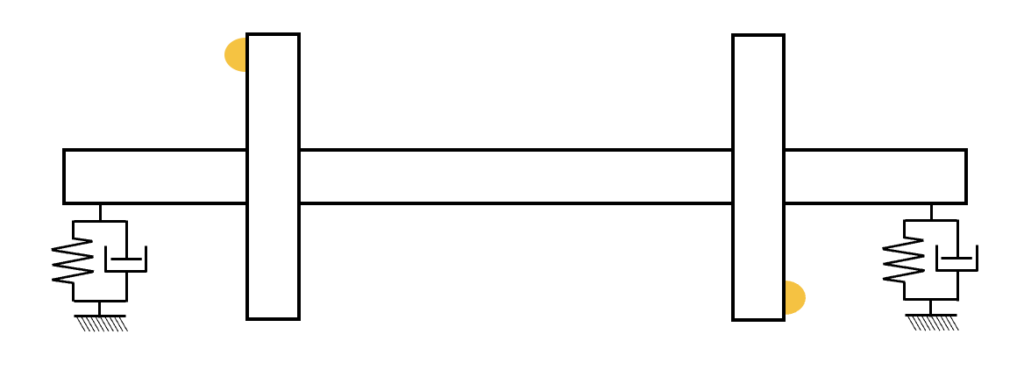
　今回扱う2面のローターモデルはこちらです。ディスクを繋ぐシャフトの長さは規定しなくても、連結剛性で表現されます。

動作環境

Pythonで2面のアンバランス振動を解析するコード

想定モデル

　コードを実装する前に、今回扱う2面のアンバランス振動を解析する対象モデルを以下に示します。
　2面の名称を考えるために、モーターと回転機のシャフトがカップリングで接続されている部分も表現しています。
　ここで、2つあるディスクのうちカップリング側を\(C\)、反対側を\(E\)と呼びます。これはCoupling sideとEnd sideという位置関係から来る名称として一般的によく使われるものです。

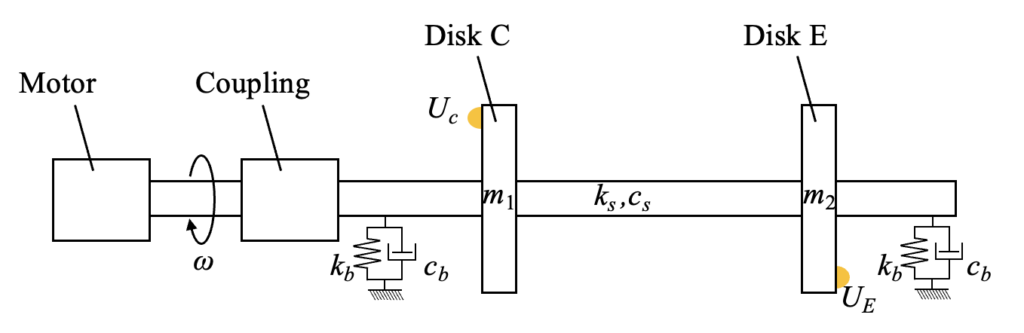
　この図には以下の考慮すべきパラメータも記載しています。

\(\omega\)：角速度 [rad/s]
\(m_{1}\)：ディスクCの質量[kg]
\(m_{2}\)：ディスクEの質量[kg]
\(k_{b}\)：BRGの支持剛性[N/m]
\(c_{b}\)：BRGの支持減衰[N·s/m]
\(k_{s}\)：シャフトの連結剛性[N/m]
\(c_{s}\)：シャフトの連結減衰[N·s/m]
\(U_{C}\)：ディスクCのアンバランス[kg·m]
\(U_{E}\)：ディスクEのアンバランス[kg·m]

　今回は2面の振動を分析することを主眼に置くので、ローターダイナミクスとして重要なジャイロ効果は無視します（別の記事で書く予定）。

運動方程式

　2面のアンバランス振動を解析するには、2枚分のディスク質量と面内振動を表現するためディスクそれぞれについて\(x, y\)方向の自由度を表現する必要があります。過去記事よりも運動方程式の数が増えてややこしくなるので、行列とベクトルを用いた式(1)を定義します。

\[ \mathbf{M}\ddot{\mathbf{q}}+\mathbf{C}\dot{\mathbf{q}}+\mathbf{K}\mathbf{q} = \mathbf{F}(t) \tag{1} \]

　ここで\(\mathbf{q}=[x_{C}, y_{C}, x_{E}, y_{E}]^\top\)と変位の状態変数を定義し、\(\dot{\mathbf{q}}\)と\(\ddot{\mathbf{q}}\)は\(\mathbf{q}\)の速度と加速度です。

　2枚のディスクと2方向の振動自由度に対応するため、質量行列は式(2)となります。

\[ \mathbf{M} = \begin{bmatrix} m_1 & 0 & 0 & 0 \\ 0 & m_1 & 0 & 0 \\ 0 & 0 & m_2 & 0 \\ 0 & 0 & 0 & m_2 \end{bmatrix} \tag{2} \]

　剛性行列と減衰行列は式(3)(4)で示されます。運動方程式は全部で4つあり、\(x_{C}, y_{C}, x_{E}, y_{E}\)それぞれに影響する力関係から接続する先を考えて行列を構築します。今回はシャフトを介して2つのディスクが互いに結合されているため、非対角項にクロス成分が入っています。仮に\(k_{s}\)と\(c_{s}\)がゼロの場合、2枚のディスクは完全に独立します。

\[ \mathbf{K} = \begin{bmatrix} k_b + k_s & 0 & -k_s & 0 \\ 0 & k_b + k_s & 0 & -k_s \\ -k_s & 0 & k_b + k_s & 0 \\ 0 & -k_s & 0 & k_b + k_s \end{bmatrix} \tag{3} \] \[ \mathbf{C} = \begin{bmatrix} c_b + c_s & 0 & -c_s & 0 \\ 0 & c_b + c_s & 0 & -c_s \\ -c_s & 0 & c_b + c_s & 0 \\ 0 & -c_s & 0 & c_b + c_s \end{bmatrix} \tag{4} \]

　外力ベクトルは式(5)です。アンバランス\(U_{C}, U_{E}\)は質量と距離の積の次元で与えられており、外力項は遠心力（\(F=mr\omega^{2}\)）を意味しています。

\[ \mathbf{F}(t) = \begin{bmatrix} \omega^2 U_C \cos(\omega t + \phi_C) \\ \omega^2 U_C \sin(\omega t + \phi_C) \\ \omega^2 U_E \cos(\omega t + \phi_E) \\ \omega^2 U_E \sin(\omega t + \phi_E) \end{bmatrix} \tag{5} \]

　これらの運動方程式は「Pythonで計算するために多自由度振動系を行列形式にする方法」で紹介した方法と同様の考え方で立てることができます。まだ慣れていない人は是非こちらの記事もみてみてください。

Pythonによる数値計算コード

　運動方程式が立てられたら、後はコードを実装して解析するだけです。次のコードをコピペして実行してみましょう。

import numpy as np
from matplotlib import pyplot as plt
from scipy.integrate import odeint


def build_matrices(m1, m2, kb, ks, cb, cs):
    """質量・剛性・減衰行列を作成する関数"""

    # 質量
    M = np.diag([m1, m1, m2, m2])

    # 剛性行列 K
    K = np.array([
        [kb + ks, 0, -ks, 0],
        [0, kb + ks, 0, -ks],
        [-ks, 0, kb + ks, 0],
        [0, -ks, 0, kb + ks]])

    # 減衰行列 C
    C = np.array([
        [cb + cs, 0, -cs, 0],
        [0, cb + cs, 0, -cs],
        [-cs, 0, cb + cs, 0],
        [0, -cs, 0, cb + cs]])

    return M, C, K


def f(var, t, Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega):
    """運動方程式：2面の回転機アンバランス振動"""
    
    q = var[0:4]
    v = var[4:8]
    pulse = var[8]
    pulse_dot = var[9]

    # アンバランス外力：力[N]
    Fxc = (omega**2) * Uc_kgm * np.cos(omega*t + phi_c)
    Fyc = (omega**2) * Uc_kgm * np.sin(omega*t + phi_c)
    Fxe = (omega**2) * Ue_kgm * np.cos(omega*t + phi_e)
    Fye = (omega**2) * Ue_kgm * np.sin(omega*t + phi_e)
    F = np.array([Fxc, Fyc, Fxe, Fye])

    # qddot = M^{-1} (F - C v - K q)
    a = Minv @ (F - C @ v - K @ q)

    # 回転パルス
    pulse_ddot = - omega**2 * np.cos(omega * t)

    return np.hstack([v, a, pulse_dot, pulse_ddot])


def plot(t, xc, yc, xe, ye, pulse, N):
    """C面とE面の結果プロットをする関数"""
    
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    fig = plt.figure(figsize=(10, 5))
    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')
    ax2 = ax1.twinx()

    ax1.set_xlabel('t[s]')
    ax1.set_ylabel('Displacement[m]')
    ax2.set_xlabel('t[s]')
    ax2.set_ylabel('Pulse[V]')

    # 最後の2周期のみ表示
    freq = N / 60
    cycle = 1.0 / freq
    dt = t[1] - t[0]
    sample_cycle = int(cycle / dt)
    i0 = max(len(t) - 2 * sample_cycle, 0)

    ax1.plot(t[i0:], xc[i0:], label='x_C', lw=3, color='red')
    ax1.plot(t[i0:], yc[i0:], label='y_C', lw=3, color='blue')
    ax1.plot(t[i0:], xe[i0:], label='x_E', lw=2.5, color='red', ls='--')
    ax1.plot(t[i0:], ye[i0:], label='y_E', lw=2.5, color='blue', ls='--')

    ax2.plot(t[i0:], pulse[i0:], label='pulse', lw=1, color='black')

    h1, l1 = ax1.get_legend_handles_labels()
    h2, l2 = ax2.get_legend_handles_labels()
    ax1.legend(h1 + h2, l1 + l2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

    fig.tight_layout()
    plt.show()
    plt.close()


if __name__ == '__main__':
    """メイン"""
    
    # C面とE面のアンバランス設定
    Uc_gmm = 100.0
    phic_deg = 0.0
    Ue_gmm = 0.0
    phie_deg = 0.0

    # 単位変換：gmm→kgm, deg.→radian
    Uc_kgm = Uc_gmm * 1e-6
    Ue_kgm = Ue_gmm * 1e-6
    phi_c = np.radians(phic_deg)
    phi_e = np.radians(phie_deg)

    # 各面の等価質量 [kg]
    m1 = 0.1  # C面
    m2 = 0.1  # E面

    # 剛性・減衰
    kb = 100.0   # 支持剛性 [N/m]
    cb = 0.1     # 支持減衰 [N·s/m]
    ks = 50.0    # 連結剛性 [N/m]
    cs = 0.05    # 連結減衰 [N·s/m]

    # 回転数と時間
    N = 100
    omega = 2 * np.pi * (N / 60)
    dt = 1e-3
    t_max = 100.0
    t = np.arange(0.0, t_max, dt)

    # 行列の構成
    M, C, K = build_matrices(m1, m2, kb, ks, cb, cs)
    Minv = np.linalg.inv(M)

    # 初期状態：[q(4)=0, v(4)=0, pulse=0, pulse_dot=0] → 10成分
    var0 = np.zeros(10)

    # 微分方程式の数値計算
    sol = odeint(
        f, var0, t,
        args=(Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega)
    )

    # 結果
    xc = sol[:, 0]
    yc = sol[:, 1]
    xe = sol[:, 2]
    ye = sol[:, 3]
    pulse = sol[:, 8]

    # プロット
    plot(t, xc, yc, xe, ye, pulse, N)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

import numpy as np

from matplotlib import pyplot as plt

from scipy.integrate import odeint

def build_matrices(m1, m2, kb, ks, cb, cs):

"""質量・剛性・減衰行列を作成する関数"""

# 質量

M = np.diag([m1, m1, m2, m2])

# 剛性行列 K

K = np.array([

[kb + ks, 0, -ks, 0],

[0, kb + ks, 0, -ks],

[-ks, 0, kb + ks, 0],

[0, -ks, 0, kb + ks]])

# 減衰行列 C

C = np.array([

[cb + cs, 0, -cs, 0],

[0, cb + cs, 0, -cs],

[-cs, 0, cb + cs, 0],

[0, -cs, 0, cb + cs]])

return M, C, K

def f(var, t, Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega):

"""運動方程式：2面の回転機アンバランス振動"""

q = var[0:4]

v = var[4:8]

pulse = var[8]

pulse_dot = var[9]

# アンバランス外力：力[N]

Fxc = (omega**2) * Uc_kgm * np.cos(omega*t + phi_c)

Fyc = (omega**2) * Uc_kgm * np.sin(omega*t + phi_c)

Fxe = (omega**2) * Ue_kgm * np.cos(omega*t + phi_e)

Fye = (omega**2) * Ue_kgm * np.sin(omega*t + phi_e)

F = np.array([Fxc, Fyc, Fxe, Fye])

# qddot = M^{-1} (F - C v - K q)

a = Minv @ (F - C @ v - K @ q)

# 回転パルス

pulse_ddot = - omega**2 * np.cos(omega * t)

return np.hstack([v, a, pulse_dot, pulse_ddot])

def plot(t, xc, yc, xe, ye, pulse, N):

"""C面とE面の結果プロットをする関数"""

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

fig = plt.figure(figsize=(10, 5))

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = ax1.twinx()

ax1.set_xlabel('t[s]')

ax1.set_ylabel('Displacement[m]')

ax2.set_xlabel('t[s]')

ax2.set_ylabel('Pulse[V]')

# 最後の2周期のみ表示

freq = N / 60

cycle = 1.0 / freq

dt = t[1] - t[0]

sample_cycle = int(cycle / dt)

i0 = max(len(t) - 2 * sample_cycle, 0)

ax1.plot(t[i0:], xc[i0:], label='x_C', lw=3, color='red')

ax1.plot(t[i0:], yc[i0:], label='y_C', lw=3, color='blue')

ax1.plot(t[i0:], xe[i0:], label='x_E', lw=2.5, color='red', ls='--')

ax1.plot(t[i0:], ye[i0:], label='y_E', lw=2.5, color='blue', ls='--')

ax2.plot(t[i0:], pulse[i0:], label='pulse', lw=1, color='black')

h1, l1 = ax1.get_legend_handles_labels()

h2, l2 = ax2.get_legend_handles_labels()

ax1.legend(h1 + h2, l1 + l2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

fig.tight_layout()

plt.show()

plt.close()

if __name__ == '__main__':

"""メイン"""

# C面とE面のアンバランス設定

Uc_gmm = 100.0

phic_deg = 0.0

Ue_gmm = 0.0

phie_deg = 0.0

# 単位変換：gmm→kgm, deg.→radian

Uc_kgm = Uc_gmm * 1e-6

Ue_kgm = Ue_gmm * 1e-6

phi_c = np.radians(phic_deg)

phi_e = np.radians(phie_deg)

# 各面の等価質量 [kg]

m1 = 0.1 # C面

m2 = 0.1 # E面

# 剛性・減衰

kb = 100.0 # 支持剛性 [N/m]

cb = 0.1 # 支持減衰 [N·s/m]

ks = 50.0 # 連結剛性 [N/m]

cs = 0.05 # 連結減衰 [N·s/m]

# 回転数と時間

N = 100

omega = 2 * np.pi * (N / 60)

dt = 1e-3

t_max = 100.0

t = np.arange(0.0, t_max, dt)

# 行列の構成

M, C, K = build_matrices(m1, m2, kb, ks, cb, cs)

Minv = np.linalg.inv(M)

# 初期状態：[q(4)=0, v(4)=0, pulse=0, pulse_dot=0] → 10成分

var0 = np.zeros(10)

# 微分方程式の数値計算

sol = odeint(

f, var0, t,

args=(Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega)

)

# 結果

xc = sol[:, 0]

yc = sol[:, 1]

xe = sol[:, 2]

ye = sol[:, 3]

pulse = sol[:, 8]

# プロット

plot(t, xc, yc, xe, ye, pulse, N)

実行結果

　上記コードは次の部分でC面側のみにアンバランスを設定しています。

# C面とE面のアンバランス設定
Uc_gmm = 100.0
phic_deg = 0.0
Ue_gmm = 0.0
phie_deg = 0.0

# C面とE面のアンバランス設定

Uc_gmm = 100.0

phic_deg = 0.0

Ue_gmm = 0.0

phie_deg = 0.0

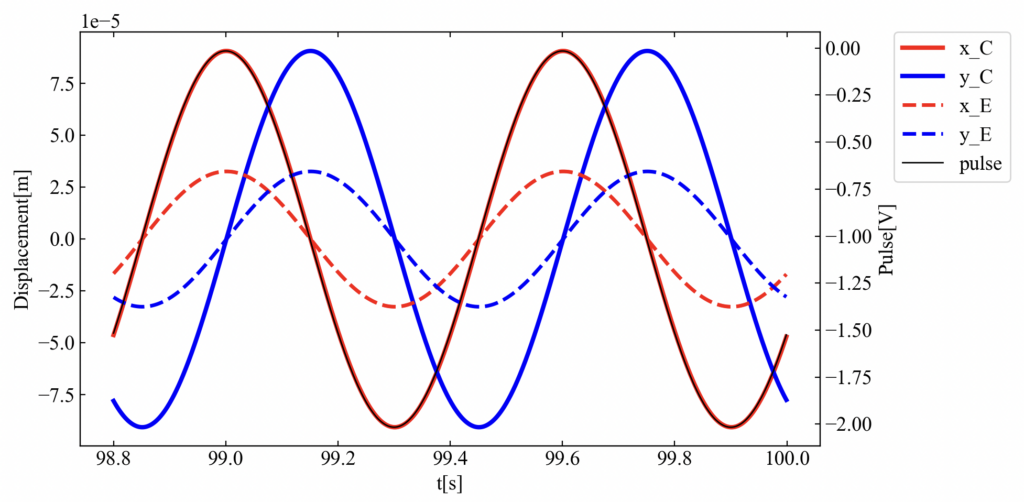
　コードを実行すると次のmatplotlibによるグラフが表示されます（振動が安定する最後の2周期分だけを表示しているため横軸は100[s]近くになっています）。このグラフはC面とE面の\(xy\)変位をプロットしていますが、C面にしかアンバランスを設定していないのにE面にも変位が発生しています。これはまさしく連結剛性と連結減衰による力の伝達が発生していることの証拠です。ちなみにC面には0°にアンバランスを設定しているため、回転パルスの位相と完全に同期しています。
　回転パルスについては「回転機の振動シミュレーションで回転パルスを設定してみた」の記事を参照してください。

実行結果：連結剛性と連結減衰をゼロにする

　コードの次の部分を変更（\(k_{s}=c_{s}=0\)）し、再度実行してみましょう。

# 剛性・減衰
kb = 100.0   # 支持剛性 [N/m]
cb = 0.1     # 支持減衰 [N·s/m]
ks = 0.0    # 連結剛性 [N/m]
cs = 0.0    # 連結減衰 [N·s/m]

# 剛性・減衰

kb = 100.0 # 支持剛性 [N/m]

cb = 0.1 # 支持減衰 [N·s/m]

ks = 0.0 # 連結剛性 [N/m]

cs = 0.0 # 連結減衰 [N·s/m]

　C面の振動は確認できますが、E面の振動がゼロになる結果を得ます。これは連結がなくなったことを意味します。

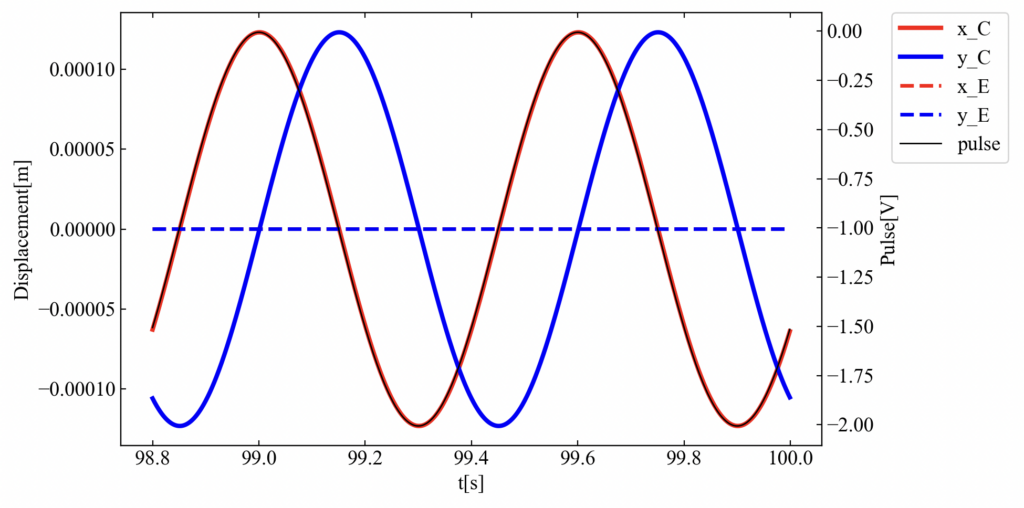
式を自分で立てているのでこの結果は自明ですが、こういう基礎検証はコードのバグ出しや理解を深めるために非常に重要です！

実行結果：連結剛性を連続的に上げていく

　\(k_{s}\)の値を少しずつ上げていって挙動を見てみましょう。次の結果は先ほどのコードのksをforループで0から1000まで上げていったものです。剛性を高くしていくとあるところでサチレートすることもわかりました。

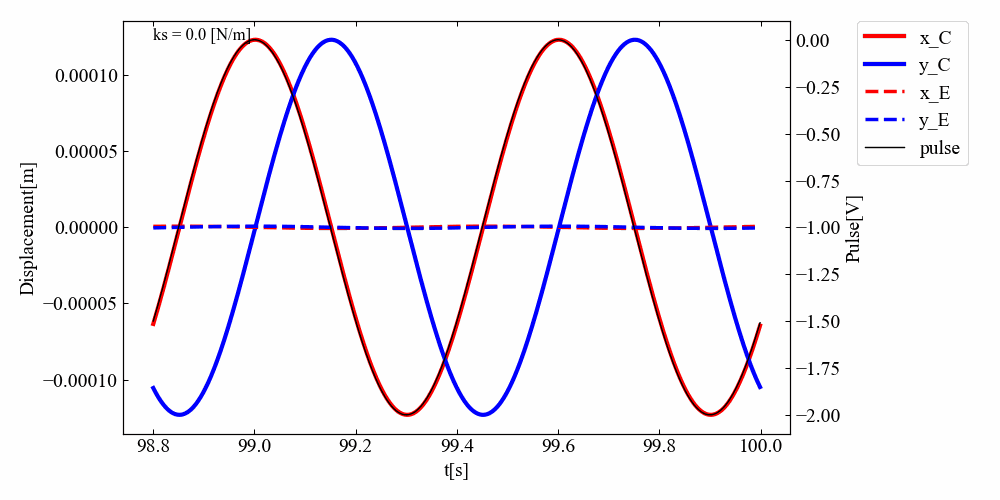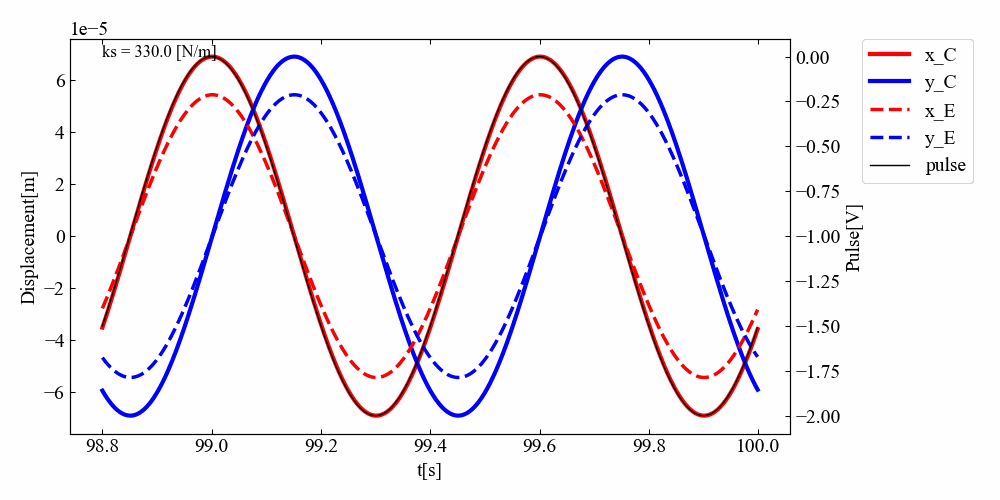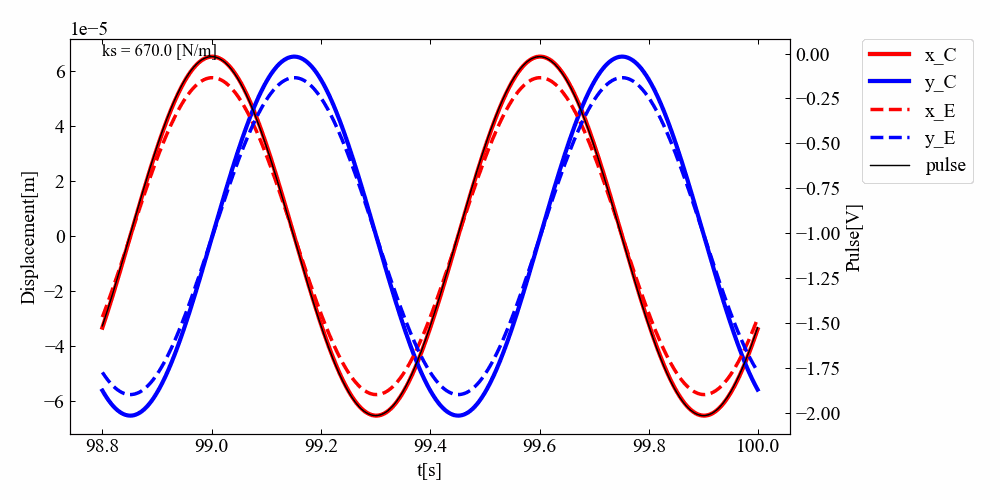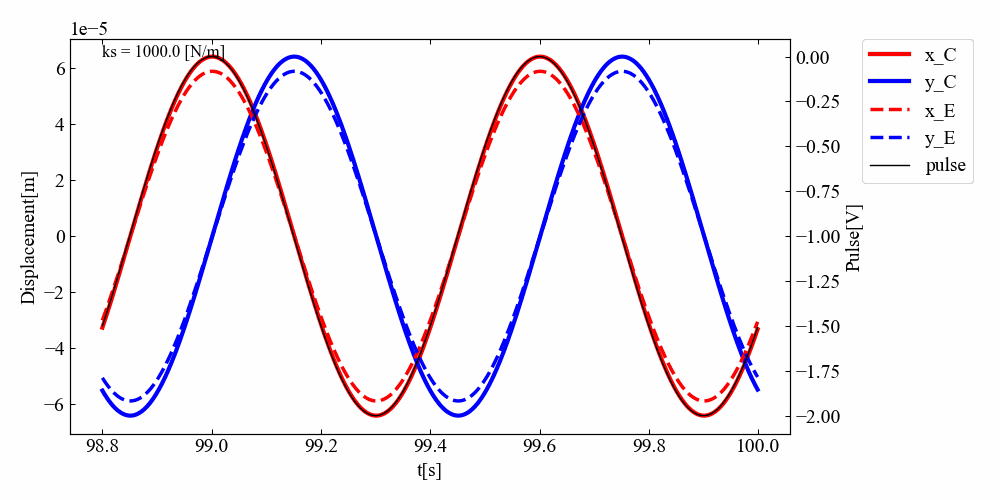
実行結果：回転数スイープ

　以下のコードで回転数をスイープさせて変位応答を確認します。

import numpy as np
from matplotlib import pyplot as plt
from scipy.integrate import odeint
from PIL import Image
import os
import glob


def build_matrices(m1, m2, kb, ks, cb, cs):
    """質量・剛性・減衰行列を作成する関数"""

    # 質量
    M = np.diag([m1, m1, m2, m2])

    # 剛性行列 K
    K = np.array([
        [kb + ks, 0, -ks, 0],
        [0, kb + ks, 0, -ks],
        [-ks, 0, kb + ks, 0],
        [0, -ks, 0, kb + ks]])

    # 減衰行列 C
    C = np.array([
        [cb + cs, 0, -cs, 0],
        [0, cb + cs, 0, -cs],
        [-cs, 0, cb + cs, 0],
        [0, -cs, 0, cb + cs]])

    return M, C, K


def f(var, t, Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega):
    """運動方程式：2面の回転機アンバランス振動"""
    
    q = var[0:4]
    v = var[4:8]
    pulse = var[8]
    pulse_dot = var[9]

    # アンバランス外力：力[N]
    Fxc = (omega**2) * Uc_kgm * np.cos(omega*t + phi_c)
    Fyc = (omega**2) * Uc_kgm * np.sin(omega*t + phi_c)
    Fxe = (omega**2) * Ue_kgm * np.cos(omega*t + phi_e)
    Fye = (omega**2) * Ue_kgm * np.sin(omega*t + phi_e)
    F = np.array([Fxc, Fyc, Fxe, Fye])

    # qddot = M^{-1} (F - C v - K q)
    a = Minv @ (F - C @ v - K @ q)

    # 回転パルス
    pulse_ddot = - omega**2 * np.cos(omega * t)

    return np.hstack([v, a, pulse_dot, pulse_ddot])


def plot(t, xc, yc, xe, ye, pulse, N, i, dir_name='img_N_variation'):
    """C面とE面の結果プロットをする関数"""
    
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    fig = plt.figure(figsize=(10, 5))
    ax1 = fig.add_subplot(111)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')
    ax2 = ax1.twinx()

    ax1.set_xlabel('t[s]')
    ax1.set_ylabel('Displacement[m]')
    ax2.set_xlabel('t[s]')
    ax2.set_ylabel('Pulse[V]')

    # 最後の2周期のみ表示
    freq = N / 60
    cycle = 1.0 / freq
    dt = t[1] - t[0]
    sample_cycle = int(cycle / dt)
    size = len(t)
    
    pulse = pulse[size - 4 * sample_cycle::]
    xc = xc[size - 4 * sample_cycle::]
    yc = yc[size - 4 * sample_cycle::]
    xe = xe[size - 4 * sample_cycle::]
    ye = ye[size - 4 * sample_cycle::]
    t = t[size - 4 * sample_cycle::]
    
    # 時間波形調節：パルス波形でトリガーをかけ、トリガー点から2周期分を抽出
    # pulse信号の範囲に基づいて適切な閾値を設定
    pulse_mean = np.mean(pulse)  # 信号の平均値を閾値として使用
    trigger_i = trigger(pulse, pulse_mean)
    
    # トリガー検出失敗時は0を閾値として再試行
    if trigger_i == -1:
        trigger_i = trigger(pulse, 0)
    
    # それでも失敗した場合は最初から2周期分を使用
    if trigger_i == -1:
        print(f"Warning: Trigger failed for N={N} rpm, using first 2 cycles")
        pulse = pulse[:2 * sample_cycle]
        xc = xc[:2 * sample_cycle]
        yc = yc[:2 * sample_cycle]
        xe = xe[:2 * sample_cycle]
        ye = ye[:2 * sample_cycle]
    else:
        # 範囲チェックを追加
        end_idx = min(trigger_i + 2 * sample_cycle, len(pulse))
        if end_idx <= len(pulse):
            pulse = pulse[trigger_i:end_idx]
            xc = xc[trigger_i:end_idx]
            yc = yc[trigger_i:end_idx]
            xe = xe[trigger_i:end_idx]
            ye = ye[trigger_i:end_idx]
        else:
            # データが不足している場合は最初から2周期分を使用
            print(f"Warning: Insufficient data after trigger for N={N} rpm")
            pulse = pulse[:2 * sample_cycle]
            xc = xc[:2 * sample_cycle]
            yc = yc[:2 * sample_cycle]
            xe = xe[:2 * sample_cycle]
            ye = ye[:2 * sample_cycle]
    
    # 空のデータでないことを確認
    if len(xc) == 0:
        print(f"Error: Empty data for N={N} rpm, frame {i}")
        return
        
    t_axis = np.arange(0, len(xc) * dt, dt)

    ax1.plot(t_axis, xc, label='x_C', lw=3, color='red')
    ax1.plot(t_axis, yc, label='y_C', lw=3, color='blue')
    ax1.plot(t_axis, xe, label='x_E', lw=2.5, color='red', ls='--')
    ax1.plot(t_axis, ye, label='y_E', lw=2.5, color='blue', ls='--')

    ax2.plot(t_axis, pulse, label='pulse', lw=1, color='black')

    # 回転数の値を表示（pulse信号の範囲に基づいて動的に位置調整）
    pulse_max = np.max(pulse)
    pulse_min = np.min(pulse)
    pulse_range = pulse_max - pulse_min
    label_y = pulse_max + pulse_range * 0.1  # 最大値の少し上
    ax2.text(0, label_y, f'N = {N:.0f} [rpm]')
    
    h1, l1 = ax1.get_legend_handles_labels()
    h2, l2 = ax2.get_legend_handles_labels()
    ax1.legend(h1 + h2, l1 + l2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

    fig.tight_layout()
    
    # 画像を保存する
    # dirフォルダが無い時に新規作成
    if not os.path.exists(dir_name):
        os.makedirs(dir_name)
    
    # 画像保存パスを準備
    path = os.path.join(dir_name, str("{:05}".format(i)) + '.png')
    
    # 画像を保存する
    #plt.show()
    plt.savefig(path)
    
    # グラフを閉じる（メモリ解放）
    plt.close()


def trigger(data, Tlevel):
    ''' トリガーをかける '''
 
    data = data - Tlevel  # 波形全体をトリガレベルでオフセット
 
    # 位置情報 i と判定値 jを初期化
    i = 0
    j = True
 
    # ゼロクロス点探査Whileループ
    # ループ停止条件＝トリガを検出した場合と検出されなかった場合のどちらか
    while j == True:
 
        # 最初のループはiを増分させるだけ
        if i == 0:
            i = i + 1
 
        # 波形を全て探査した場合はjを強制的に判定値jをFalseにしてiに-1（未検出の意味）を代入
        elif i + 1 == len(data):
            j = False
            i = -1
        # 前の値(i-1)と今の値(i)で符号を比較し判定値jに渡す。iを増分させる。
        else:
            if np.sign(data[i - 1]) != np.sign(data[i]):
                j = data[i - 1] > data[i]
            i = i + 1
 
    return i


def create_gif(in_dir, out_filename):
    ''' imgフォルダの複数画像からGIF画像を作る '''
 
    # ファイルパスをソートしてリストする
    path_list = sorted(glob.glob(os.path.join(*[in_dir, '*'])))
 
    # ファイルのフルパスからファイル名と拡張子を抽出
    imgs = []
    for i in range(len(path_list)):
        img = Image.open(path_list[i])
        imgs.append(img)
 
    # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。
    imgs[0].save(out_filename,
                 save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0)
 
    return


if __name__ == '__main__':
    """メイン"""
    
    # C面とE面のアンバランス設定
    Uc_gmm = 100.0
    phic_deg = 0.0
    Ue_gmm = 0.0
    phie_deg = 0.0

    # 単位変換：gmm→kgm, deg.→radian
    Uc_kgm = Uc_gmm * 1e-6
    Ue_kgm = Ue_gmm * 1e-6
    phi_c = np.radians(phic_deg)
    phi_e = np.radians(phie_deg)

    # 各面の等価質量 [kg]
    m1 = 0.1  # C面
    m2 = 0.1  # E面

    # 剛性・減衰
    kb = 100.0   # 支持剛性 [N/m]
    cb = 0.1     # 支持減衰 [N·s/m]
    ks = 50.0    # 連結剛性 [N/m]
    cs = 0.05    # 連結減衰 [N·s/m]

    # 回転数と時間
    N_list = np.arange(100, 1001, 10)
    
    dt = 1e-3
    t_max = 100.0
    t = np.arange(0.0, t_max, dt)
    
    # 画像保存用フォルダ
    dir_name = 'img_N_variation'
    
    # フォルダが無い時に新規作成
    if not os.path.exists(dir_name):
        os.makedirs(dir_name)
    
    for i in range(len(N_list)):
        N = N_list[i]
        print(f"Processing: N = {N} [rpm] ({i+1}/{len(N_list)})")
        
        # 角速度
        omega = 2 * np.pi * (N / 60)

        # 行列の構成
        M, C, K = build_matrices(m1, m2, kb, ks, cb, cs)
        Minv = np.linalg.inv(M)

        # 初期状態：[q(4)=0, v(4)=0, pulse=0, pulse_dot=0] → 10成分
        var0 = np.zeros(10)

        # 微分方程式の数値計算
        sol = odeint(
            f, var0, t,
            args=(Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega)
        )

        # 結果
        xc = sol[:, 0]
        yc = sol[:, 1]
        xe = sol[:, 2]
        ye = sol[:, 3]
        pulse = sol[:, 8]

        # プロット（保存）
        plot(t, xc, yc, xe, ye, pulse, N, i, dir_name)
    
    # GIF動画を作成する
    print("Creating GIF animation...")
    create_gif(dir_name, 'N_variation_animation.gif')
    print("GIF animation created: N_variation_animation.gif")

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

128

129

130

131

132

133

134

135

136

137

138

139

140

141

142

143

144

145

146

147

148

149

150

151

152

153

154

155

156

157

158

159

160

161

162

163

164

165

166

167

168

169

170

171

172

173

174

175

176

177

178

179

180

181

182

183

184

185

186

187

188

189

190

191

192

193

194

195

196

197

198

199

200

201

202

203

204

205

206

207

208

209

210

211

212

213

214

215

216

217

218

219

220

221

222

223

224

225

226

227

228

229

230

231

232

233

234

235

236

237

238

239

240

241

242

243

244

245

246

247

248

249

250

251

252

253

254

255

256

257

258

259

260

261

262

263

264

265

266

267

268

269

270

271

272

273

274

275

276

277

278

279

280

281

282

283

284

285

286

287

288

import numpy as np

from matplotlib import pyplot as plt

from scipy.integrate import odeint

from PIL import Image

import os

import glob

def build_matrices(m1, m2, kb, ks, cb, cs):

"""質量・剛性・減衰行列を作成する関数"""

# 質量

M = np.diag([m1, m1, m2, m2])

# 剛性行列 K

K = np.array([

[kb + ks, 0, -ks, 0],

[0, kb + ks, 0, -ks],

[-ks, 0, kb + ks, 0],

[0, -ks, 0, kb + ks]])

# 減衰行列 C

C = np.array([

[cb + cs, 0, -cs, 0],

[0, cb + cs, 0, -cs],

[-cs, 0, cb + cs, 0],

[0, -cs, 0, cb + cs]])

return M, C, K

def f(var, t, Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega):

"""運動方程式：2面の回転機アンバランス振動"""

q = var[0:4]

v = var[4:8]

pulse = var[8]

pulse_dot = var[9]

# アンバランス外力：力[N]

Fxc = (omega**2) * Uc_kgm * np.cos(omega*t + phi_c)

Fyc = (omega**2) * Uc_kgm * np.sin(omega*t + phi_c)

Fxe = (omega**2) * Ue_kgm * np.cos(omega*t + phi_e)

Fye = (omega**2) * Ue_kgm * np.sin(omega*t + phi_e)

F = np.array([Fxc, Fyc, Fxe, Fye])

# qddot = M^{-1} (F - C v - K q)

a = Minv @ (F - C @ v - K @ q)

# 回転パルス

pulse_ddot = - omega**2 * np.cos(omega * t)

return np.hstack([v, a, pulse_dot, pulse_ddot])

def plot(t, xc, yc, xe, ye, pulse, N, i, dir_name='img_N_variation'):

"""C面とE面の結果プロットをする関数"""

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

fig = plt.figure(figsize=(10, 5))

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = ax1.twinx()

ax1.set_xlabel('t[s]')

ax1.set_ylabel('Displacement[m]')

ax2.set_xlabel('t[s]')

ax2.set_ylabel('Pulse[V]')

# 最後の2周期のみ表示

freq = N / 60

cycle = 1.0 / freq

dt = t[1] - t[0]

sample_cycle = int(cycle / dt)

size = len(t)

pulse = pulse[size - 4 * sample_cycle::]

xc = xc[size - 4 * sample_cycle::]

yc = yc[size - 4 * sample_cycle::]

xe = xe[size - 4 * sample_cycle::]

ye = ye[size - 4 * sample_cycle::]

t = t[size - 4 * sample_cycle::]

# 時間波形調節：パルス波形でトリガーをかけ、トリガー点から2周期分を抽出

# pulse信号の範囲に基づいて適切な閾値を設定

pulse_mean = np.mean(pulse) # 信号の平均値を閾値として使用

trigger_i = trigger(pulse, pulse_mean)

# トリガー検出失敗時は0を閾値として再試行

if trigger_i == -1:

trigger_i = trigger(pulse, 0)

# それでも失敗した場合は最初から2周期分を使用

if trigger_i == -1:

print(f"Warning: Trigger failed for N={N} rpm, using first 2 cycles")

pulse = pulse[:2 * sample_cycle]

xc = xc[:2 * sample_cycle]

yc = yc[:2 * sample_cycle]

xe = xe[:2 * sample_cycle]

ye = ye[:2 * sample_cycle]

else:

# 範囲チェックを追加

end_idx = min(trigger_i + 2 * sample_cycle, len(pulse))

if end_idx <= len(pulse):

pulse = pulse[trigger_i:end_idx]

xc = xc[trigger_i:end_idx]

yc = yc[trigger_i:end_idx]

xe = xe[trigger_i:end_idx]

ye = ye[trigger_i:end_idx]

else:

# データが不足している場合は最初から2周期分を使用

print(f"Warning: Insufficient data after trigger for N={N} rpm")

pulse = pulse[:2 * sample_cycle]

xc = xc[:2 * sample_cycle]

yc = yc[:2 * sample_cycle]

xe = xe[:2 * sample_cycle]

ye = ye[:2 * sample_cycle]

# 空のデータでないことを確認

if len(xc) == 0:

print(f"Error: Empty data for N={N} rpm, frame {i}")

return

t_axis = np.arange(0, len(xc) * dt, dt)

ax1.plot(t_axis, xc, label='x_C', lw=3, color='red')

ax1.plot(t_axis, yc, label='y_C', lw=3, color='blue')

ax1.plot(t_axis, xe, label='x_E', lw=2.5, color='red', ls='--')

ax1.plot(t_axis, ye, label='y_E', lw=2.5, color='blue', ls='--')

ax2.plot(t_axis, pulse, label='pulse', lw=1, color='black')

# 回転数の値を表示（pulse信号の範囲に基づいて動的に位置調整）

pulse_max = np.max(pulse)

pulse_min = np.min(pulse)

pulse_range = pulse_max - pulse_min

label_y = pulse_max + pulse_range * 0.1 # 最大値の少し上

ax2.text(0, label_y, f'N = {N:.0f} [rpm]')

h1, l1 = ax1.get_legend_handles_labels()

h2, l2 = ax2.get_legend_handles_labels()

ax1.legend(h1 + h2, l1 + l2, bbox_to_anchor=(1.1, 1), loc='upper left', borderaxespad=0.)

fig.tight_layout()

# 画像を保存する

# dirフォルダが無い時に新規作成

if not os.path.exists(dir_name):

os.makedirs(dir_name)

# 画像保存パスを準備

path = os.path.join(dir_name, str("{:05}".format(i)) + '.png')

# 画像を保存する

#plt.show()

plt.savefig(path)

# グラフを閉じる（メモリ解放）

plt.close()

def trigger(data, Tlevel):

''' トリガーをかける '''

data = data - Tlevel # 波形全体をトリガレベルでオフセット

# 位置情報 i と判定値 jを初期化

i = 0

j = True

# ゼロクロス点探査Whileループ

# ループ停止条件＝トリガを検出した場合と検出されなかった場合のどちらか

while j == True:

# 最初のループはiを増分させるだけ

if i == 0:

i = i + 1

# 波形を全て探査した場合はjを強制的に判定値jをFalseにしてiに-1（未検出の意味）を代入

elif i + 1 == len(data):

j = False

i = -1

# 前の値(i-1)と今の値(i)で符号を比較し判定値jに渡す。iを増分させる。

else:

if np.sign(data[i - 1]) != np.sign(data[i]):

j = data[i - 1] > data[i]

i = i + 1

return i

def create_gif(in_dir, out_filename):

''' imgフォルダの複数画像からGIF画像を作る '''

# ファイルパスをソートしてリストする

path_list = sorted(glob.glob(os.path.join(*[in_dir, '*'])))

# ファイルのフルパスからファイル名と拡張子を抽出

imgs = []

for i in range(len(path_list)):

img = Image.open(path_list[i])

imgs.append(img)

# appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。

imgs[0].save(out_filename,

save_all=True, append_images=imgs[1:], optimize=False, duration=200, loop=0)

return

if __name__ == '__main__':

"""メイン"""

# C面とE面のアンバランス設定

Uc_gmm = 100.0

phic_deg = 0.0

Ue_gmm = 0.0

phie_deg = 0.0

# 単位変換：gmm→kgm, deg.→radian

Uc_kgm = Uc_gmm * 1e-6

Ue_kgm = Ue_gmm * 1e-6

phi_c = np.radians(phic_deg)

phi_e = np.radians(phie_deg)

# 各面の等価質量 [kg]

m1 = 0.1 # C面

m2 = 0.1 # E面

# 剛性・減衰

kb = 100.0 # 支持剛性 [N/m]

cb = 0.1 # 支持減衰 [N·s/m]

ks = 50.0 # 連結剛性 [N/m]

cs = 0.05 # 連結減衰 [N·s/m]

# 回転数と時間

N_list = np.arange(100, 1001, 10)

dt = 1e-3

t_max = 100.0

t = np.arange(0.0, t_max, dt)

# 画像保存用フォルダ

dir_name = 'img_N_variation'

# フォルダが無い時に新規作成

if not os.path.exists(dir_name):

os.makedirs(dir_name)

for i in range(len(N_list)):

N = N_list[i]

print(f"Processing: N = {N} [rpm] ({i+1}/{len(N_list)})")

# 角速度

omega = 2 * np.pi * (N / 60)

# 行列の構成

M, C, K = build_matrices(m1, m2, kb, ks, cb, cs)

Minv = np.linalg.inv(M)

# 初期状態：[q(4)=0, v(4)=0, pulse=0, pulse_dot=0] → 10成分

var0 = np.zeros(10)

# 微分方程式の数値計算

sol = odeint(

f, var0, t,

args=(Minv, C, K, Uc_kgm, Ue_kgm, phi_c, phi_e, omega)

)

# 結果

xc = sol[:, 0]

yc = sol[:, 1]

xe = sol[:, 2]

ye = sol[:, 3]

pulse = sol[:, 8]

# プロット（保存）

plot(t, xc, yc, xe, ye, pulse, N, i, dir_name)

# GIF動画を作成する

print("Creating GIF animation...")

create_gif(dir_name, 'N_variation_animation.gif')

print("GIF animation created: N_variation_animation.gif")

　こちらが実行結果です。結構面白い結果となったと思います。「回転機の振動シミュレーションで回転パルスを設定してみた」の記事で共振を過ぎると位相が反転することはわかっていましたが、ディスクが2つになると反転時にアンバランスを設定していない面の振幅が一瞬高くなる様子が確認されました。共振後はC面側の位相はずれたままですが、E面側の位相は元の位置に戻るようです。

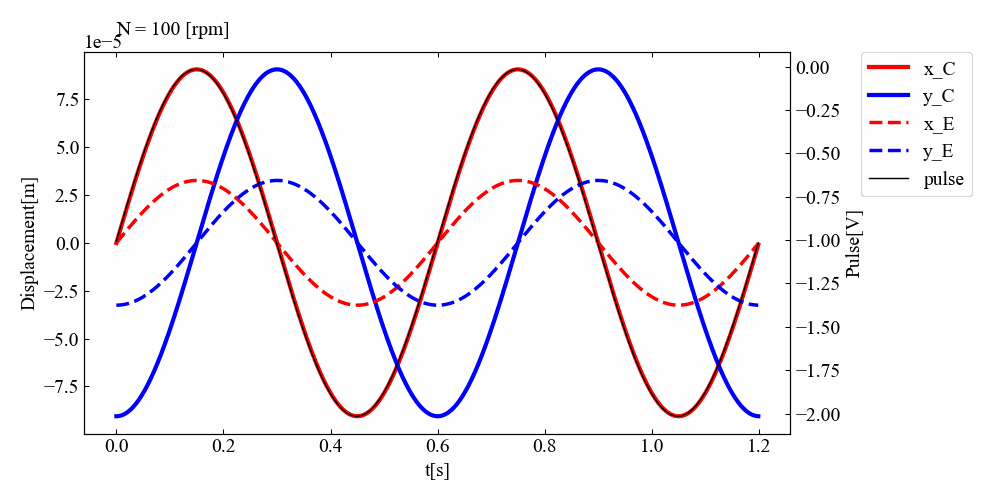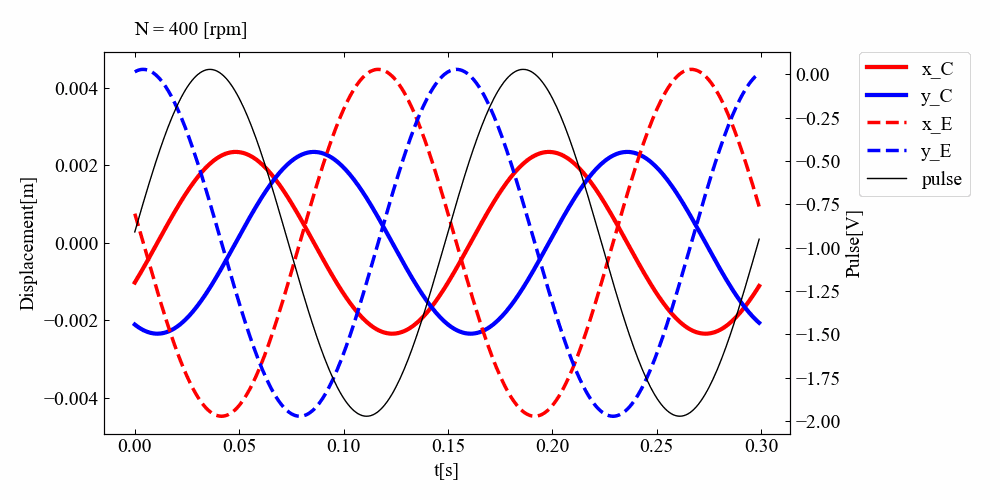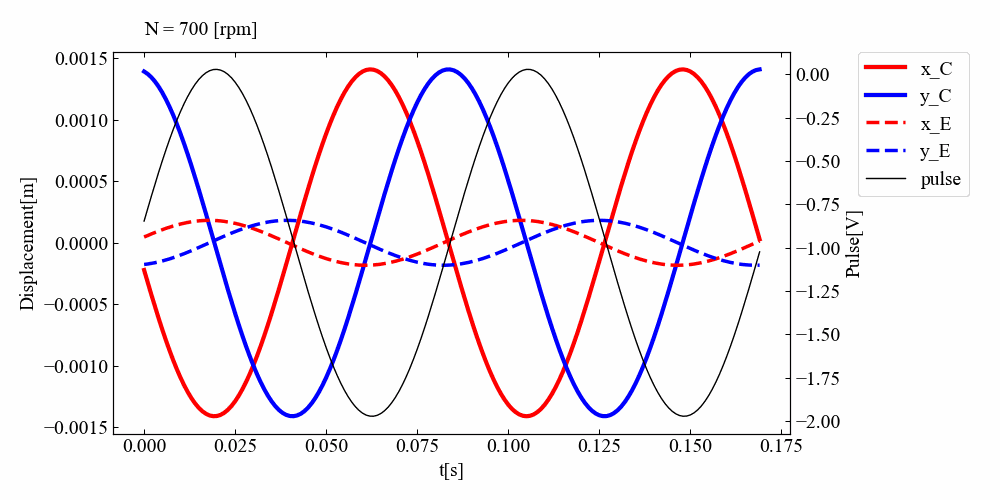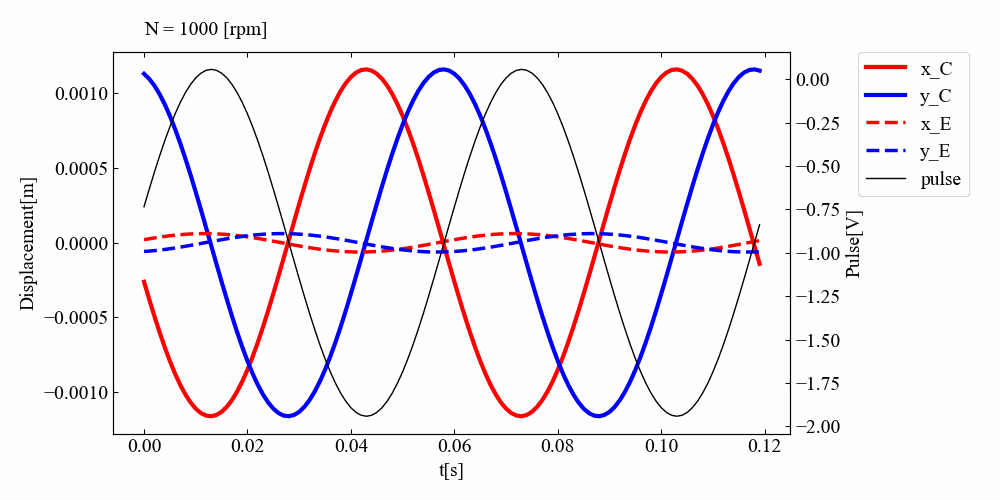
なぜこのような挙動になるんだ！？今はわかりませんが（コードのバグ？）、モードが関係していそうだという予想します。わかる方、ご教示いただけると助かります。

まとめ

　本記事はジェフコットローター（Jeffcott Rotor）の2面アンバランス振動をシミュレーションする運動方程式とコードを紹介しました。ジャイロ効果は考慮していませんが、連結剛性や回転数を変化させた時の挙動は特徴的であることがわかりました。
　このブログでは単純に技術的興味から本コードを書いてみましたが、面白いのでジャイロ効果やバランシング計算の調査も行ってみようと思います。今の時代（生成AI時代）、単純なジェフコットローターであれば追加の要素もそんなに苦もなく入れられるのではと思います。

単面だけでなく、2面の回転機シミュレーションもできるようになりました！
Xでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

Pythonでジェフコットローターの2面アンバランス振動を計算する

この記事のモチベーション

2面のアンバランス振動を解析する

前回記事のおさらい

なぜ2面で振動を確認したいか？

UnbalanceとImbalanceについて

2面を考慮したジェフコットローター

動作環境

Pythonで2面のアンバランス振動を解析するコード

想定モデル

運動方程式

Pythonによる数値計算コード

実行結果

実行結果：連結剛性と連結減衰をゼロにする

実行結果：連結剛性を連続的に上げていく

実行結果：回転数スイープ

まとめ

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

この記事のモチベーション

2面のアンバランス振動を解析する

前回記事のおさらい

なぜ2面で振動を確認したいか？

UnbalanceとImbalanceについて

2面を考慮したジェフコットローター

動作環境

Pythonで2面のアンバランス振動を解析するコード

想定モデル

運動方程式

Pythonによる数値計算コード

実行結果

実行結果：連結剛性と連結減衰をゼロにする

実行結果：連結剛性を連続的に上げていく

実行結果：回転数スイープ

まとめ

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル