数値解析の分野ではガウス積分という求積手法がよく用いられます。ガウス積分はルジャンドル多項式を使って積分点と重みを算出しますが、初学者はまずこれらの概念を理解するのが難しいです。この記事では簡単な関数を題材にガウス積分を計算する方法をPythonコードと共に紹介します。
こんにちは。wat（@watlablog）です。今回は数値解析の主要技術の1つ、ガウス積分をPythonで書いてみます！
動作環境
この記事ではPythonコードを挟みながら説明しますが、以下のPython環境で動作確認をしました。
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.23.0 |
| matplotlib | 3.7.1 |
ガウス積分の概要
ガウス積分の定義式
ガウス積分、またはガウス求積（Gaussian Quadrature）とは、関数の積分値を近似計算する手法の一つです。この手法は特定の積分区間において、関数の値を積分点（ガウス点）で評価します。
関数\(f(x)\)を\([a, b]\)の積分区間でガウス積分をする定義式を（1）に示します。
ここで\(x_{i}\)が積分点の位置、\(w_{i}\)が\(i\)番目の積分点における重み（weightings）です。\(n\)が積分点の個数で次数（order）とも呼ばれます。\(n\)次ガウス積分は\(2n-1\)次の多項式の積分値を正確に求めることができる特徴を持ちます。
積分の近似計算にはその他にも台形公式やシンプソン則を用いるものがありますが、高精度かつ計算回数の少なさからくる高速性が数値解析で使われる理由となっています。
積分点の求め方：ルジャンドル多項式を利用する
式（1）のガウス積分では積分点の位置を知る必要があります。積分点はルジャンドル多項式（Legendre polynomials）のゼロ点を用います（ルジャンドル多項式については以下の外部サイトがわかりやすいと思います）。
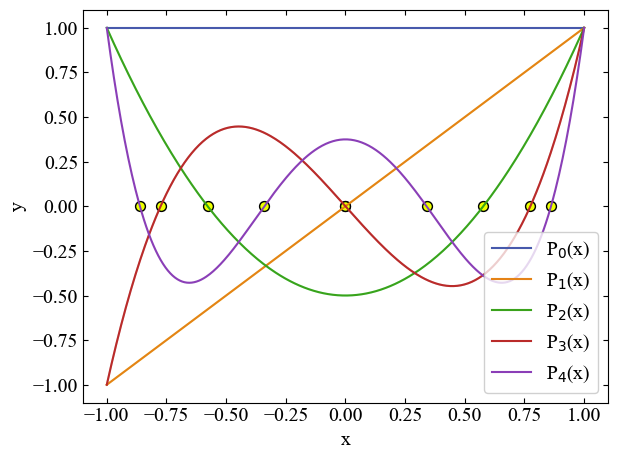
百聞は一見にしかずということで、ルジャンドル多項式を可視化してみましょう。以下のPythonコードを実行することで各次数の多項式プロットとゼロ点を可視化できます。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 |
import numpy as np import matplotlib.pyplot as plt # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの入れ物を用意する。 fig = plt.figure() ax1 = fig.add_subplot(111) # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # グラフの上下左右に目盛線を付ける。 ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') x = np.linspace(-1, 1, 400) for n in range(5): # 最初の4つのルジャンドル多項式をプロット # ルジャンドル多項式を求める y = np.polynomial.legendre.legval(x, [0]*n + [1]) ax1.plot(x, y, label=f'P$_{n}$(x)') # 交点を求める roots = np.polynomial.legendre.legroots([0] * n + [1]) ax1.scatter(roots, np.zeros_like(roots), color='yellow', edgecolors='black', s=50) ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() |
こちらがグラフです。ルジャンドル多項式は[-1, 1]の範囲で定義される正規直交多項式であり、次数に応じて異なる数のゼロ点を持つ特徴があります。
変数変換
実際の被積分関数は必ずしも[-1, 1]の範囲にあるわけではないので、式（2）の関係式を使って変数変換する必要があります。
式（2）は\(\xi=\)-1の時\(x=a\)、\(\xi=\)1の時\(x=b\)となります。
実際には先にルジャンドル多項式から積分点を計算しておき、式（1）でガウス積分を計算する段階で変数変換を反映させます。[-1, 1]の範囲におけるガウス積分式は式（3）です。
式（2）の変換式を考慮すると、積分の演算子は式（4）の関係を持ちます。
式（4）を考慮すると変数変換を考慮したガウス積分は式（5）になります。
それではこの内容をPythonでコーディングしてみましょう！
Pythonでガウス積分するコード(イメージ図付き)
理論や証明は難しいですが、使うだけなら簡単です。以下に任意の関数をガウス積分するコードを示します。f関数のreturnに関数形状を書きます。ルジャンドル多項式はnp.polynomial.legendre.leggaussを使って求めます。積分区間a, bと次数nを設定して実行してみましょう。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 |
import numpy as np from matplotlib import pyplot as plt def f(x): """ 被積分関数 """ return x ** 2 def gaussian_quadrature(f, start, end, n): """ ガウス積分をする関数 """ # 次数nにおけるガウス点と重みを取得する xi, weights = np.polynomial.legendre.leggauss(n) print(xi) # 積分区間の変換をする x = 0.5 * (end - start) * xi + 0.5 * (end + start) print(x) # 積分する integral_result = 0.5 * (b - a) * sum(weights * f(x)) print('Integral value=', integral_result) # プロットで可視化する plot(x, weights, n) return integral_result def plot(x, weights, n): """ グラフ描画する関数 """ x_val = np.linspace(-0.2, 2.2, 100) y_val = f(x_val) # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('f(x)') # データをプロットする。 ax1.plot(x_val, y_val, label='f(x)') for i in range(n): # 積分点 ax1.scatter(x[i], f(x[i]), color='yellow', edgecolors='black', s=100, label='Gauss points' if i == 0 else "") # 重みが反映された矩形 width = weights[i] * (b - a) / 2 ax1.fill_between([x[i] - width / 2, x[i] + width / 2], 0, f(x[i]), color='skyblue', alpha=0.5, label='Weighted area' if i == 0 else "") ax1.legend() # グラフを表示する。 fig.tight_layout() plt.show() plt.close() return if __name__ == '__main__': """ Main """ # 積分区間[a, b]と積分点の数を指定してガウス積分をする a, b = 0, 2 n = 2 result = gaussian_quadrature(f, a, b, n) |
まずはn=2の結果です。黄色点で積分点（ガウス点）、矩形エリアに重みを考慮した面積をプロットしています。
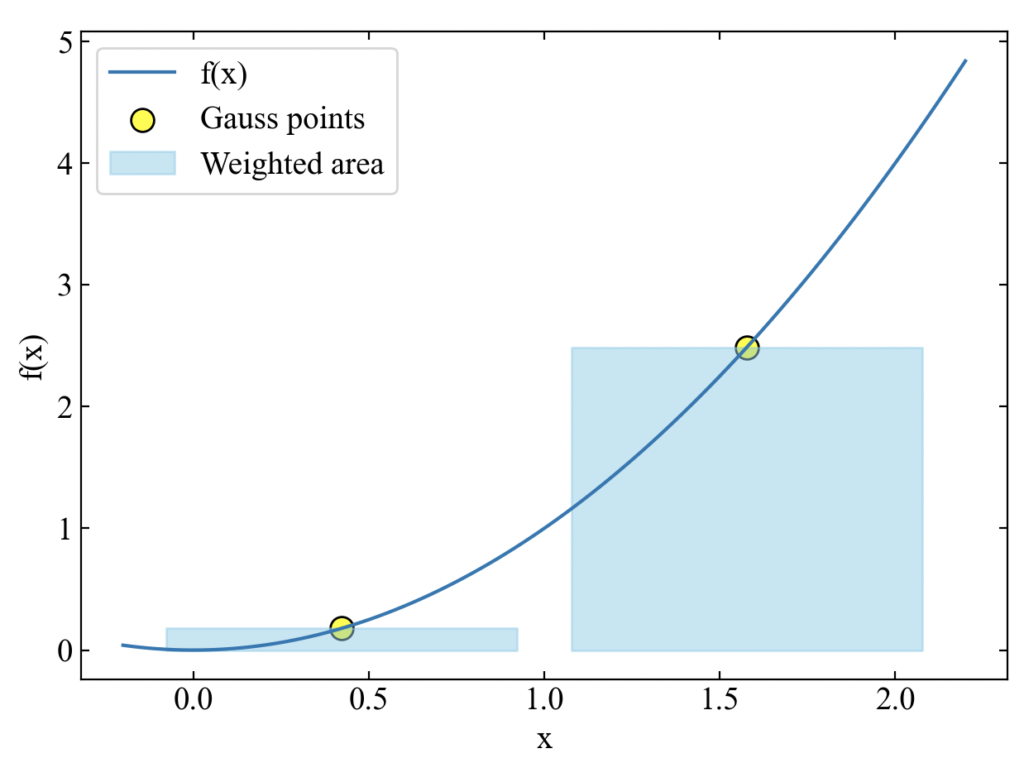
出力ウィンドウには「Integral value= 2.666666666666667」と出ていますが、式（6）から理論値と一致していることが確認できます。
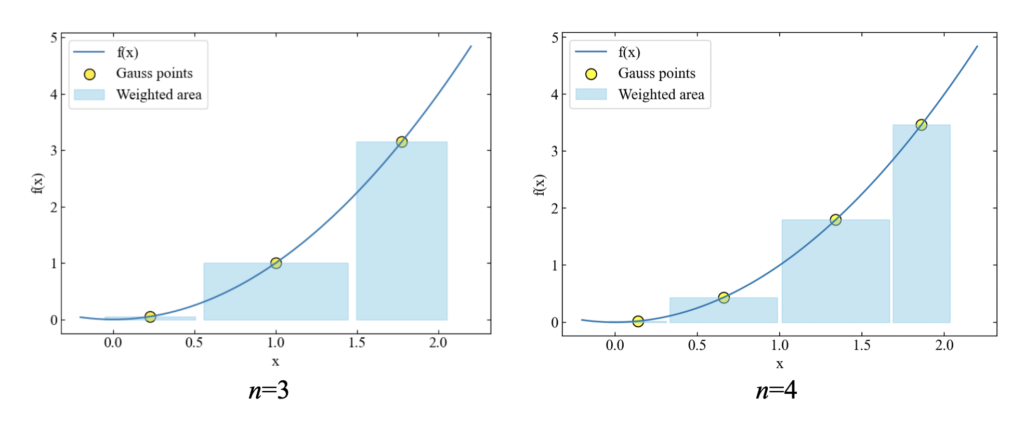
以下は次数違いの積分結果です。ガウス積分の特性から、積分値はほぼ変わりませんが矩形形状の幅寸法が重みによって変わる様子を確認できると思います。
まとめ
本日はここまで。
この記事ではガウス積分を使って積分値を近似計算するための関連式を紹介し、Pythonで計算する方法を紹介しました。
ガウス積分をするためにはルジャンドル多項式を使い積分点と重みを算出する必要があること、そして変数変換が必要であることを学びました。
最後はmatplotlibを使い可視化を行うことで、ガウス積分のイメージを掴むことができました。
今後は多重積分における使用等に進みたいと思います。
また、以下の記事で有限要素法を学び始めたので、有限要素法の計算に取り入れるにはどうしたら良いかも考えていきたいと思います。
難しいと思っていたガウス積分も使うだけなら簡単でした！
Xでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！