フーリエ変換をする際、漏れ誤差の改善のために一般的に窓関数を用います。ここではiOSアプリ開発でも窓関数の適用ができるようSwiftによる窓関数の適用方法を紹介し、実際に時間波形に対して適用、グラフ表示まで行います。
こんにちは。wat(@watlablog)です。ここではSwiftUIを使った信号処理コードシリーズとして窓関数の実装を紹介します！
窓関数のおさらい
WATLABブログはPythonに関する情報発信を基本としていましたので、窓関数については以下の記事でそれぞれ紹介をしていました。この記事でも窓関数の概要は説明しますが、筆者と同じくPythonの方が得意な読者はこちらの記事を是非参照してみてください。
・PythonでFFT!SciPyで窓関数をかける
・Pythonで窓関数が無い場合は？指数窓を自作してみる！
・窓関数使用時の補正！FFTの時に忘れがちな計算とは？
いつも正しい周期で波形を切り出して分析できれば良いのですが、実際は様々な周波数成分の信号に対して全てキリよく抽出することができません。中途半端な信号をフーリエ変換した場合に振幅スペクトルが分散してしまう漏れ誤差（Leakage error）が発生してしまいます。これを軽減するために窓関数が使われます\(^{[1]}\)。
概要の説明はPython記事に任せて、この記事では早速SwiftUIでコーディングを始めたいと思います！
SwiftUIで窓関数を実装する
動作環境
本記事のコードは以下の環境で動作を確認しました。
| Mac | OS | macOS Ventura 13.2.1 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] | |
| Xcode | Version | 14.3(14E222b) |
| Swift | Version | 5.8(swiftlang-5.8.0.124.2 clang-1403.0.22.11.100) |
| iPhone SE2 | OS | iOS 16.3.1 |
ハニング窓
まずは最も使用頻度の高いハニング窓（通称ハン窓）を書いてみます。ハニング窓は式（1）で示されます。\(w(t)\)は窓関数計算後の波形です。ハニング窓がよく使われる理由としては、時間波形に含まれる振動数と振幅をともに精度よく分析できるから\(^{[1]}\)だそうです。
Swiftの関数で書いたコードがこちらです。データ点数Nを引数とし、ハニング窓をかけた後の波形を返す関数にしてみました。
|
1 2 3 4 5 6 |
func hanningWindow(N: Int) -> [Float] { // ハニング窓 let w = (0..<N).map { 0.5 - 0.5 * cos(2.0 * .pi * Float($0) / Float(N - 1)) } return w } |
GUIとしてChartにグラフ表示するところまで書いた全コードを以下に示します。このコードはwavePoints関数で理想的な正弦波を作ってChartに表示させるプログラムに対して、間に窓関数の適用を挟んだ構成で書いています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 |
import SwiftUI import Charts import Accelerate struct PointsData: Identifiable { // 点群データの構造体 var xValue: Float var yValue: Float var id = UUID() } struct ContentView: View { // データを定義 @State private var data: [PointsData] = [] @State private var x: [Float] = [] @State private var y: [Float] = [] @State private var showingAlert = false func linspace(start: Float, stop: Float, num: Int) -> [Float] { // データ点数を指定して配列を作成する関数 let increment = (stop - start) / Float(num - 1) return (0..<num).map { Float($0) * increment + start } } func wavePoints(N: Int, length: Float) -> (xArray: [Float], yArray: [Float]){ // プロットするデータを演算する関数 // データ点数Nと時間長lengthからx軸を作成 let xArray = linspace(start: 0.0, stop: length, num: N) // 正弦波を作成。A:振幅、f:周波数[Hz]、dc:直流成分 let A: Float = 1 let f: Float = 10 let dc: Float = 0 let yArray = xArray.map{ A * sin(2 * .pi * f * $0) + dc } return (xArray, yArray) } func hanningWindow(N: Int) -> [Float] { // ハニング窓 let w = (0..<N).map { 0.5 - 0.5 * cos(2.0 * .pi * Float($0) / Float(N - 1)) } return w } var body: some View { // UI VStack{ Chart { // データ構造からx, y値を取得してプロット ForEach(data) { shape in LineMark( x: .value("x", shape.xValue), y: .value("y", shape.yValue) ) } } .padding(.all, 10) Button("Button"){ // ボタンイベント // 関数を実行してx, y演算結果を取得 let result = wavePoints(N: 500, length: 1) let x = result.xArray var y = result.yArray // ハニング窓関数を適用 let window = hanningWindow(N: x.count) y = zip(y, window).map(*) // プロットデータの全削除 data.removeAll() // プロットデータの追加 data.append(contentsOf: zip(x, y).map { PointsData(xValue: $0, yValue: $1) }) } } } } struct ContentView_Previews: PreviewProvider { static var previews: some View { // プレビュー ContentView() } } |
下図が実行結果です。Buttonという文字をクリックすると両端が0になった波形が表示されます。
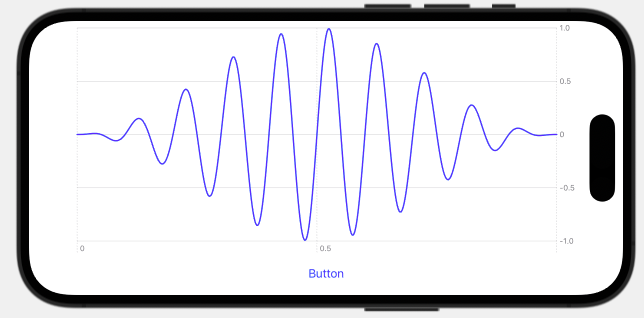
フラットトップ窓
続いてよく使われる窓関数の例として、もう一つフラットトップ窓を紹介します。フラットトップ窓は式（2）で示されます。この窓関数は周波数分解能を犠牲にして振幅成分をより精密に分析する時に使います。
こちらが関数です。一度に式を書いたら「The compiler is unable to type-check this expression in reasonable time; try breaking up the expression into distinct sub-expressions」というメッセージが出たので、いくつかの式に分割して最後にまとめるという方法で書いてみました。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 |
func flatTopWindow(N: Int) -> [Float] { // フラットトップ窓関数 let a0: Float = 1.0 let a1: Float = 1.93 let a2: Float = 1.29 let a3: Float = 0.388 let a4: Float = 0.032 let w = (0..<N).map { n in let term1 = a0 let term2 = a1 * cos(2 * .pi * Float(n) / Float(N - 1)) let term3 = a2 * cos(4 * .pi * Float(n) / Float(N - 1)) let term4 = a3 * cos(6 * .pi * Float(n) / Float(N - 1)) let term5 = a4 * cos(8 * .pi * Float(n) / Float(N - 1)) return term1 - term2 + term3 - term4 + term5 } return w } |
以下に実行結果を示します。中心付近の振動成分がより目立つような形になりました。
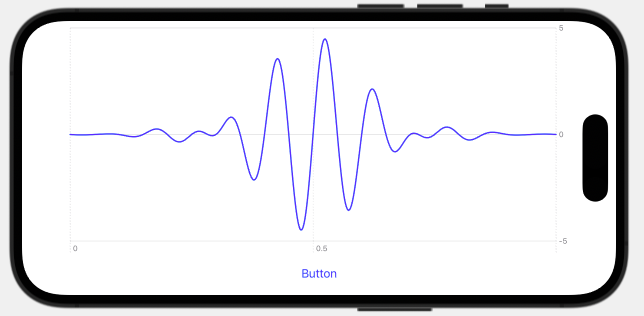
まとめ
本日はここまで。Swift系の記事は一度Pythonでやった内容を書き直すような作業であるため簡単にしています。とはいえ、Pythonでは窓関数もライブラリを使って適用していたのに対し、Swiftでは自分で式を組み込むということをしてみました。
窓関数の式の違いにより周波数波形にどう違いが出てくるかといった細かい話はいずれどこかでまとめるかも知れません。
参考文献
[1]:永井健一, 丸山真一, システム計測工学 ポイントでわかる機械計測の基礎と実践, 森北出版, 2011, pp112-115Swiftでも窓関数を実装するやり方がわかりました！
Twitter（今はXと呼ぶ？）でも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！