Pythonで学ぶ周波数変調(FM)！変調式と特徴を見てみる

周波数が変動している信号を周波数変調信号（FM信号）と呼びます。ここでは周波数変調式と各パラメータの意味を紹介し、Pythonによるヒルベルト変換やフーリエ変換を駆使してAM信号とは異なるFM信号の周波数特性を観察してみましょう。

こんにちは。wat(@watlablog)です。ここでは周波数変調を持った波について式やPythonによる周波数分析を紹介します！

周波数変調波の概要

無変調波と振幅変調波の復習

基本波の式と例

周波数変調波を学ぶ前に、基本の波である無変調波と振幅変調波の復習をしておきましょう。
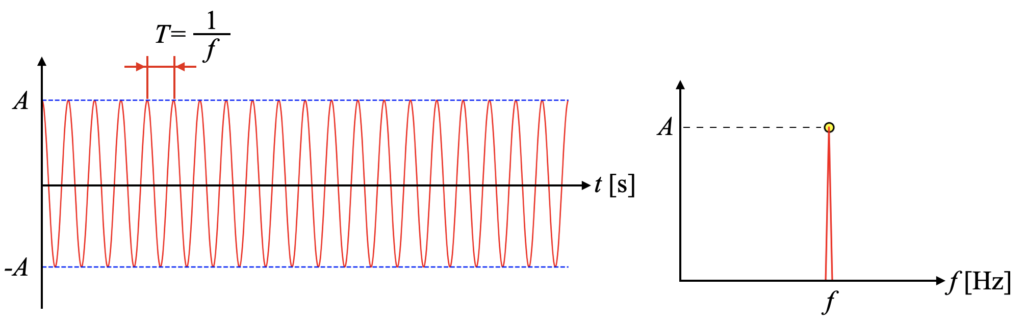
変調のない基本的な波$s(t)$は次の式(1)で表現します。

\[ s(t)=A \cos (2 \pi f t) \tag{1} \]

振幅変調波の式と例

一方、振幅変調波は式(2)で表現され、基本波（キャリア波）の周波数$f_{c}$とは別に振幅成分の振動に対する周波数$f_{m}$が組み込まれた形をしています。

\[ s(t)=A\left\{1 + m \cos(2 \pi f_{m} t) \right \} \cos (2 \pi f_{c} t) \tag{2} \]

プロットはこちら。振幅成分は振動していますが、周波数は一定です。

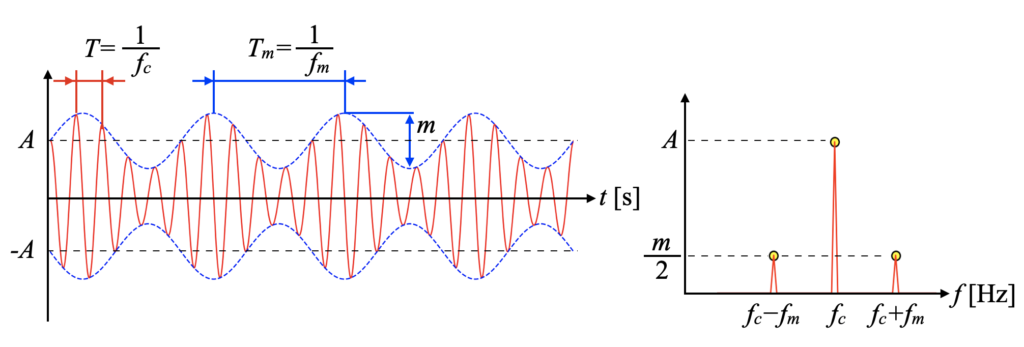
ただ、面白いことにフーリエスペクトルには主次数の周りに3つのピーク（+低周波に変動成分の次数が1つ）が現れます。詳しくは既に「Pythonで学ぶ信号処理！振幅変調のサイドバンドを観察してみる」で解説していますので、ご興味がある方はこちらの記事をご覧ください。

周波数変調波

周波数変調波の例

周波数変調（FM：Frequency Modulation）とは、周波数が変動していることを意味します。周波数変調した波の例を下図に示します。

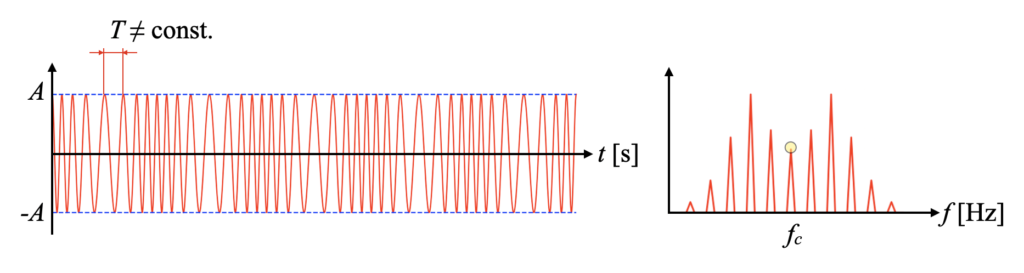
このように、振幅が一定であっても振動数自体が時間で変化する特徴を左図の時間波形からも確認できます。

さらに振幅変調の場合は右図フーリエスペクトルにおいて、主次数の周りに立つサイドバンド（側帯波）の振幅と周波数成分が明確に説明できたのに対し、周波数変調の場合は簡単に説明できないという特徴があります。

周波数領域における次数の立ち方は実際にPythonで式のパラメータを振ってプロットしながら考えていきましょう。

周波数変調の式

周波数変調波は式(3)で描くことができます。
式中のパラメータは振幅$A$、キャリア周波数$f_{c}$、変調周波数$f_{m}$、変調指数$\beta$（$f_{m}$の変動幅$\Delta f$と$f_{m}$の比）で構成されます。

\[ \begin{eqnarray} s(t)&=&A\cos \left \{(2 \pi f_{c} t) + \beta \sin (2 \pi f_{m} t) \right \}\\ \beta &=& \frac{\Delta f}{f_{m}} \end{eqnarray} \tag{3} \]

周波数変調は何に使われる？

通信技術

周波数変調波はFM波の名の通り、FMラジオや無線機器（アマチュア無線や無線LAN等）で活用されています。周波数変調を施した処理と逆の操作をすることで信号を復調できることも振幅変調の記事で解説した通りです。

振幅にノイズが混ざっても対策がとりやすかったり、振幅変調よりもダイナミックレンジがとりやすいというメリットもあります。

振動騒音技術

周波数変調は振動騒音技術にも活用されます。
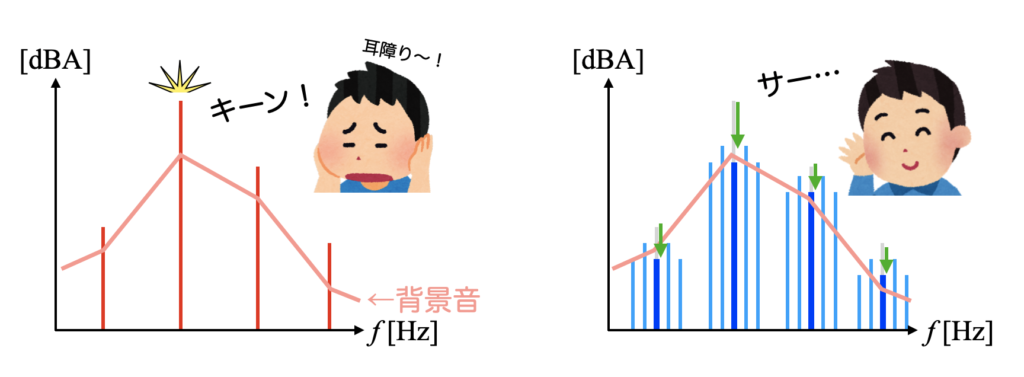
例えばある工業製品の作動音が特定周波数で非常に高いピークを持っている場合、その音色は人間にとって耳障りな音になるでしょう。

周波数変調は主次数の周りにサイドバンドが立ちますが、主次数の振幅を変化させることが可能であるため、音色がマイルドになる特徴を持ちます。実際の工業製品には既に周波数変調を応用した低騒音技術が適用されているものも多くあります。

下図のように、製品開発で音色まで配慮することができれば、製品の魅力を向上させる一つの手段となるでしょう。

Pythonで周波数変調波を分析してみるコード

それでは早速Pythonを使って周波数変調波を生成し、周波数分析をしてみましょう！Pythonは上記式(3)をほぼそのまま書いて波を作ることができます。

開発環境

以下のPython開発環境で確認を行いました。おなじみのnumpy、フーリエ変換や後述するヒルベルト変換のためのscipy、可視化のためのmatplotlibをpip installしておきましょう。

Python	Python 3.9.6
PyCharm (IDE)	PyCharm CE 2020.1
Numpy	1.21.1
Scipy	1.4.1
matplotlib	3.4.3

参考知識

フーリエ変換

ここからは普通にフーリエ変換を使っていきます。もしフーリエ変換を使った周波数分析コードについて曖昧なところがある場合は、以下の記事をご確認ください。

PythonでFFT実装!SciPyのフーリエ変換まとめ

ヒルベルト変換

今回は周波数を変調させた波について分析を行いますが、ヒルベルト変換を使うことで瞬時振幅と瞬時周波数を計算可能です。

これらは瞬間の振幅と周波数ですので、式で意図した通りに波が作れているかという検証で活用します。

ヒルベルト変換は実信号を互いに直交する複素信号を使って表現する面白い技術です。以下の記事で詳細を解説していますので、是非こちらも併せてご確認ください。

Pythonでヒルベルト変換!時間波形の包絡線を求める方法

全コード

以下に全コードを示します。
可読性のため信号生成、フーリエ変換、ヒルベルト変換、プロットはそれぞれdef関数でまとめ、最後にメインコード内でシーケンシャルにコールしている構成です。

import numpy as np
from scipy import fftpack
import matplotlib.pyplot as plt

def create_fm(t, A, fc, fm, beta):
    '''周波数変調波を生成'''
    s = A * np.cos((2 * np.pi * fc * t) + beta * np.sin(2 * np.pi * fm * t))
    return s

def calc_fft(data, samplerate):
    '''フーリエ変換'''
    spectrum = fftpack.fft(data)
    amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2))
    amp = amp / (len(data) / 2)
    #phase = np.arctan2(spectrum.imag, spectrum.real)
    #phase = np.degrees(phase)
    freq = np.linspace(0, samplerate, len(data))
    return amp, freq

def plot(t, y, instantaneous_amp, instantaneous_frequency, fft_amp, fft_axis, beta):
    '''matplotlibで可視化'''
    # フォントの種類とサイズを設定する。
    plt.rcParams['font.size'] = 14
    plt.rcParams['font.family'] = 'Times New Roman'

    # 目盛を内側にする。
    plt.rcParams['xtick.direction'] = 'in'
    plt.rcParams['ytick.direction'] = 'in'

    # グラフの上下左右に目盛線を付ける。
    fig = plt.figure(figsize=(12, 5))
    ax1 = fig.add_subplot(221)
    ax1.yaxis.set_ticks_position('both')
    ax1.xaxis.set_ticks_position('both')
    ax2 = fig.add_subplot(223)
    ax2.yaxis.set_ticks_position('both')
    ax2.xaxis.set_ticks_position('both')
    ax3 = fig.add_subplot(122)
    ax3.yaxis.set_ticks_position('both')
    ax3.xaxis.set_ticks_position('both')

    # 軸のラベルを設定する。
    ax1.set_xlabel('Time [s]')
    ax1.set_ylabel('Amplitude')
    ax2.set_xlabel('Time [s]')
    ax2.set_ylabel('Frequency [Hz]')
    ax3.set_xlabel('Frequency [Hz]')
    ax3.set_ylabel('Amplitude')

    # スケール設定
    ax1.set_ylim(-2, 2)
    ax2.set_ylim(0, 20)
    ax3.set_xlim(0, 20)
    ax3.set_ylim(0, 1)

    # データプロット
    ax1.plot(t, y, label='data', lw=1, color='red')
    ax1.plot(t, instantaneous_amp, label='instantaneous amplitude', lw=1, color='blue', linestyle='dashed')
    ax1.plot(t, -instantaneous_amp, lw=1, color='blue', linestyle='dashed')
    ax2.plot(t, instantaneous_frequency, label='instantaneous frequency', lw=1, color='blue')
    ax3.plot(fft_axis, fft_amp, label='fm waveform', lw=1, color='red')

    # テキストプロット
    plt.text(1, 0.9, '$\\beta$=' + str(round(beta, 2)), fontsize=16)

    # レイアウト設定
    fig.tight_layout()
    ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)
    ax2.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)
    ax3.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)

    # グラフを表示する。
    plt.show()
    plt.close()

def hilbert(yt, dt):
    '''ヒルベルト変換'''
    # フーリエ変換
    spectrum = fftpack.fft(yt)

    # 負周波数域（ナイキスト周波数以降）を0にする（実部と虚部の両方）
    zeros = np.zeros(int(len(spectrum) / 2))
    spectrum[int(len(spectrum)/2):len(spectrum)] = zeros

    # 正周波数域（ナイキスト周波数まで）を2倍する
    spectrum *= 2

    #実部と虚部から瞬時振幅と瞬時位相を計算する
    zt = fftpack.ifft(spectrum)
    re = zt.real
    im = zt.imag

    # 瞬時振幅
    instantaneous_amp = np.sqrt(re ** 2 + im ** 2)

    # 瞬時位相とアンラップ処理
    instantaneous_phase = np.arctan2(im, re)
    instantaneous_phase = np.unwrap(instantaneous_phase)

    # 瞬時周波数（位相角の微分と時間刻み影響を考慮）
    instantaneous_frequency = ((1 / dt) / (2 * np.pi)) * np.gradient(instantaneous_phase)

    return instantaneous_amp, instantaneous_frequency, instantaneous_phase

if __name__ == '__main__':
    # 周波数変調信号の設定(キャリア信号振幅Ac, キャリア信号周波数fc, 変調周波数fm, 変動幅f_delta)
    A = 1
    fc = 10
    fm = 1
    f_delta = 4
    beta = f_delta / fm

    # 時間刻みと時間軸
    dt = 0.0001
    t = np.arange(0, 10, dt)

    # 周波数変調波を取得
    y = create_fm(t, A, fc, fm, beta)

    # ヒルベルト変換を実行して瞬時振幅, 瞬時周波数, 瞬時位相を得る
    instantaneous_amp, instantaneous_frequency, instantaneous_phase = hilbert(y, dt)

    # フーリエ変換を実行
    amp, freq = calc_fft(y, 1/dt)

    # プロットを表示
    plot(t, y, instantaneous_amp, instantaneous_frequency, amp, freq, beta)

100

101

102

103

104

105

106

107

108

109

110

111

112

113

114

115

116

117

118

119

120

121

122

123

124

125

126

127

import numpy as np

from scipy import fftpack

import matplotlib.pyplot as plt

def create_fm(t, A, fc, fm, beta):

'''周波数変調波を生成'''

s = A * np.cos((2 * np.pi * fc * t) + beta * np.sin(2 * np.pi * fm * t))

return s

def calc_fft(data, samplerate):

'''フーリエ変換'''

spectrum = fftpack.fft(data)

amp = np.sqrt((spectrum.real ** 2) + (spectrum.imag ** 2))

amp = amp / (len(data) / 2)

#phase = np.arctan2(spectrum.imag, spectrum.real)

#phase = np.degrees(phase)

freq = np.linspace(0, samplerate, len(data))

return amp, freq

def plot(t, y, instantaneous_amp, instantaneous_frequency, fft_amp, fft_axis, beta):

'''matplotlibで可視化'''

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# グラフの上下左右に目盛線を付ける。

fig = plt.figure(figsize=(12, 5))

ax1 = fig.add_subplot(221)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

ax2 = fig.add_subplot(223)

ax2.yaxis.set_ticks_position('both')

ax2.xaxis.set_ticks_position('both')

ax3 = fig.add_subplot(122)

ax3.yaxis.set_ticks_position('both')

ax3.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_xlabel('Time [s]')

ax1.set_ylabel('Amplitude')

ax2.set_xlabel('Time [s]')

ax2.set_ylabel('Frequency [Hz]')

ax3.set_xlabel('Frequency [Hz]')

ax3.set_ylabel('Amplitude')

# スケール設定

ax1.set_ylim(-2, 2)

ax2.set_ylim(0, 20)

ax3.set_xlim(0, 20)

ax3.set_ylim(0, 1)

# データプロット

ax1.plot(t, y, label='data', lw=1, color='red')

ax1.plot(t, instantaneous_amp, label='instantaneous amplitude', lw=1, color='blue', linestyle='dashed')

ax1.plot(t, -instantaneous_amp, lw=1, color='blue', linestyle='dashed')

ax2.plot(t, instantaneous_frequency, label='instantaneous frequency', lw=1, color='blue')

ax3.plot(fft_axis, fft_amp, label='fm waveform', lw=1, color='red')

# テキストプロット

plt.text(1, 0.9, '$\\beta$=' + str(round(beta, 2)), fontsize=16)

# レイアウト設定

fig.tight_layout()

ax1.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)

ax2.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)

ax3.legend(bbox_to_anchor=(1, 1), loc='upper right', borderaxespad=0, fontsize=8)

# グラフを表示する。

plt.show()

plt.close()

def hilbert(yt, dt):

'''ヒルベルト変換'''

# フーリエ変換

spectrum = fftpack.fft(yt)

# 負周波数域（ナイキスト周波数以降）を0にする（実部と虚部の両方）

zeros = np.zeros(int(len(spectrum) / 2))

spectrum[int(len(spectrum)/2):len(spectrum)] = zeros

# 正周波数域（ナイキスト周波数まで）を2倍する

spectrum *= 2

#実部と虚部から瞬時振幅と瞬時位相を計算する

zt = fftpack.ifft(spectrum)

re = zt.real

im = zt.imag

# 瞬時振幅

instantaneous_amp = np.sqrt(re ** 2 + im ** 2)

# 瞬時位相とアンラップ処理

instantaneous_phase = np.arctan2(im, re)

instantaneous_phase = np.unwrap(instantaneous_phase)

# 瞬時周波数（位相角の微分と時間刻み影響を考慮）

instantaneous_frequency = ((1 / dt) / (2 * np.pi)) * np.gradient(instantaneous_phase)

return instantaneous_amp, instantaneous_frequency, instantaneous_phase

if __name__ == '__main__':

# 周波数変調信号の設定(キャリア信号振幅Ac, キャリア信号周波数fc, 変調周波数fm, 変動幅f_delta)

A = 1

fc = 10

fm = 1

f_delta = 4

beta = f_delta / fm

# 時間刻みと時間軸

dt = 0.0001

t = np.arange(0, 10, dt)

# 周波数変調波を取得

y = create_fm(t, A, fc, fm, beta)

# ヒルベルト変換を実行して瞬時振幅, 瞬時周波数, 瞬時位相を得る

instantaneous_amp, instantaneous_frequency, instantaneous_phase = hilbert(y, dt)

# フーリエ変換を実行

amp, freq = calc_fft(y, 1/dt)

# プロットを表示

plot(t, y, instantaneous_amp, instantaneous_frequency, amp, freq, beta)

実行結果

$\beta=0$

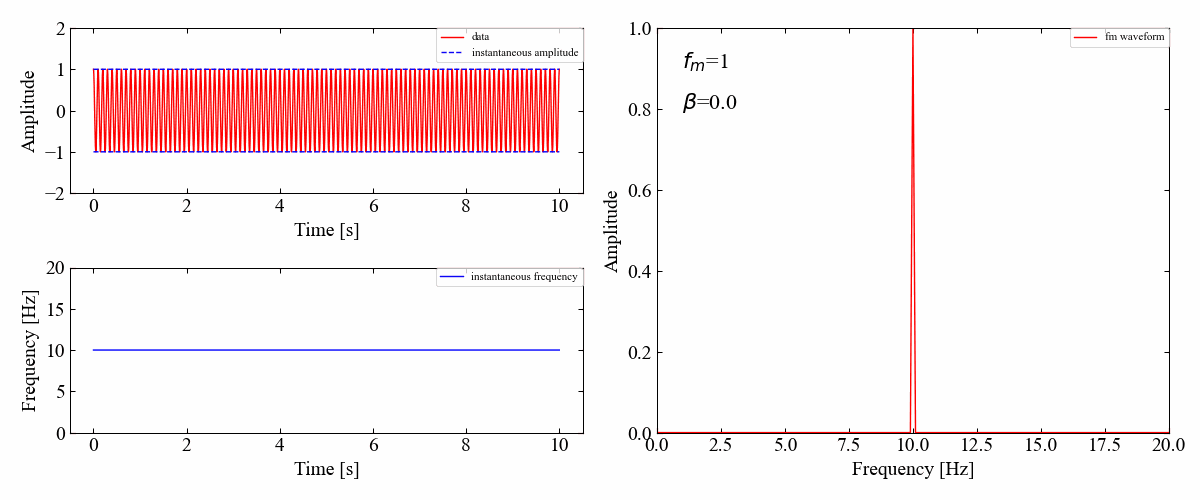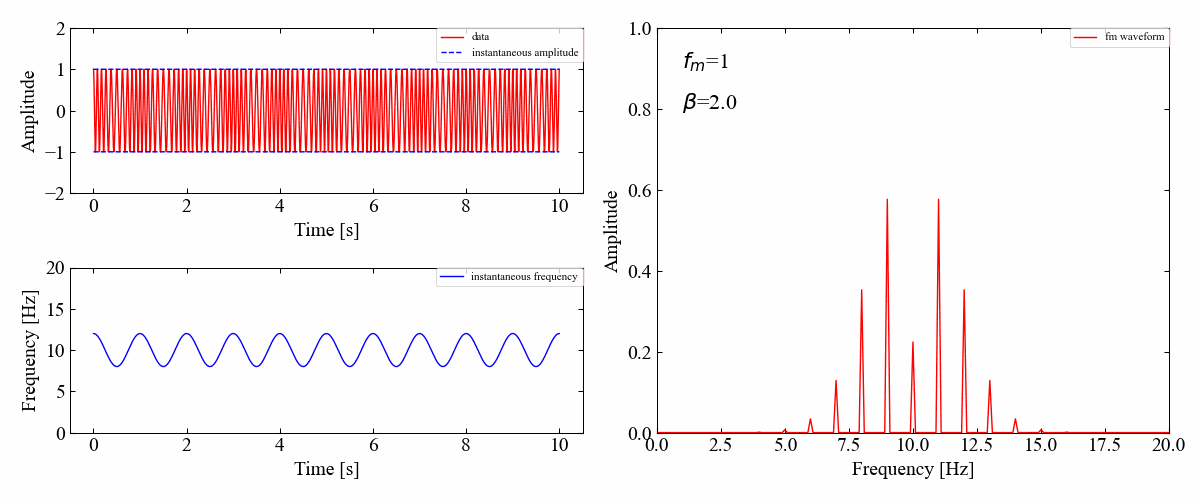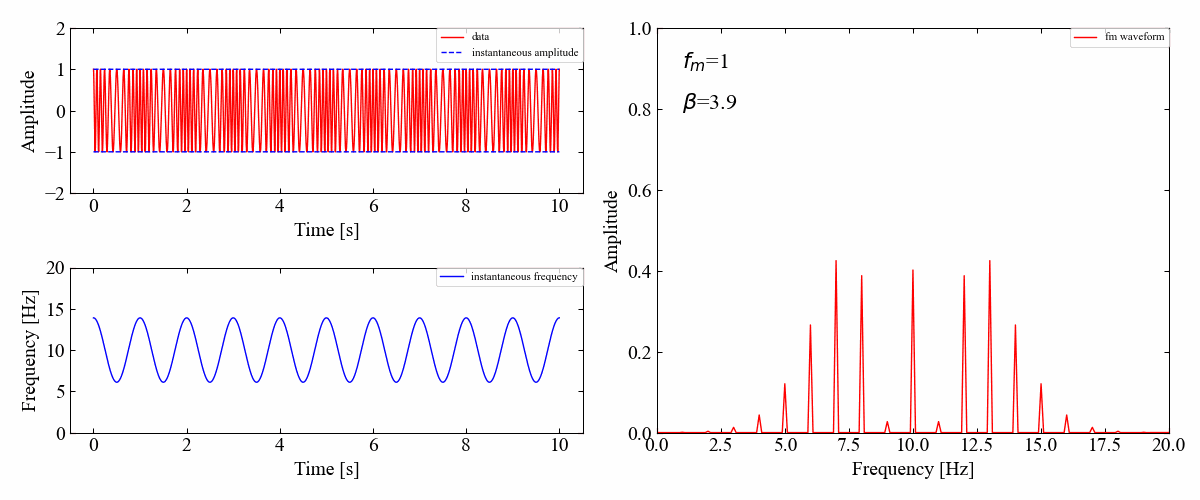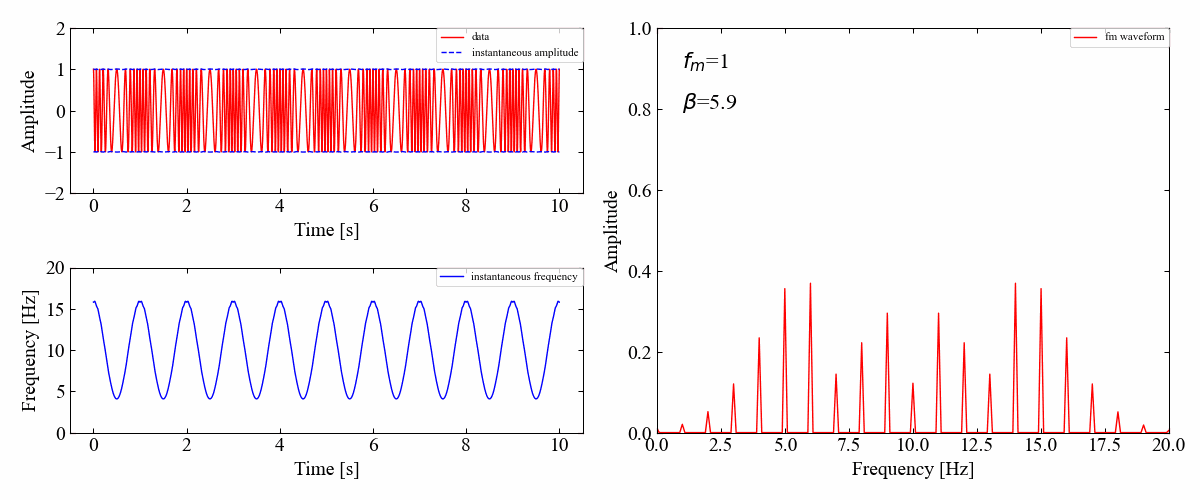
f_delta＝0にすることで、無変調の波とすることができます。これは純粋な基本波であり、変調指数$\beta=0$の結果です。

周波数波形の振幅成分が1になることを確認しました。もちろん左下の瞬時周波数は時間によって変化しません。

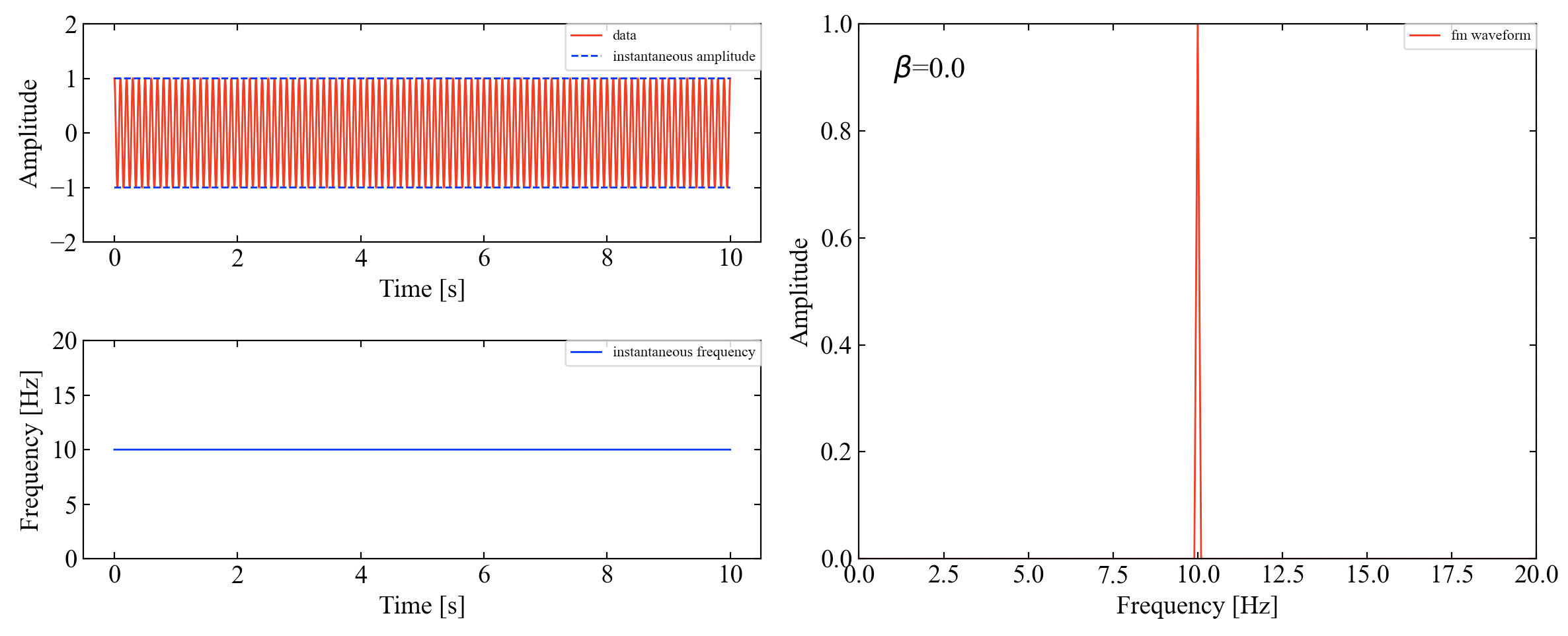
$\beta=0.5$

f_deltaを操作して$\beta=0.5$にしてみました。サイドバンドの発生と主次数がやや低下していることを確認しました。

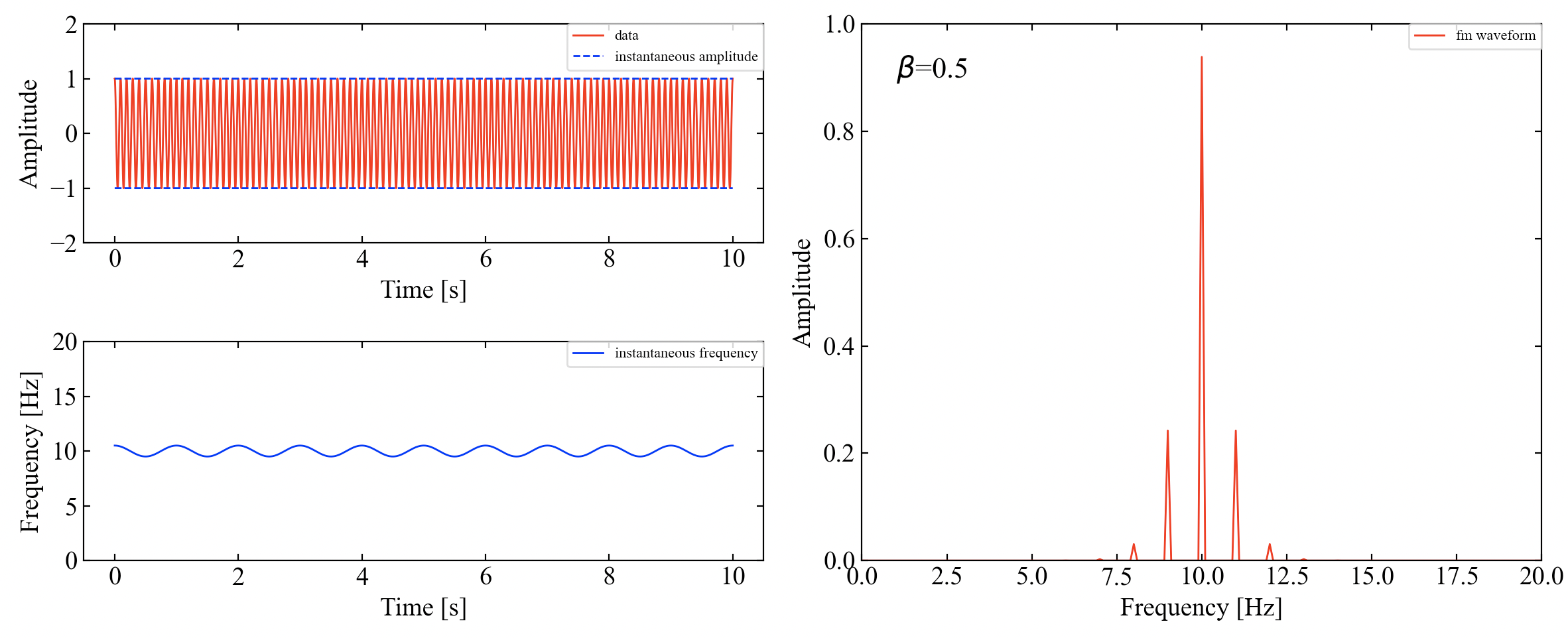
次に変調周波数fm=1→2と変化させ、$\beta$の値が同じになるようf_deltaを調整した結果を示します。先ほどとはサイドバンドの間隔が変わりました。

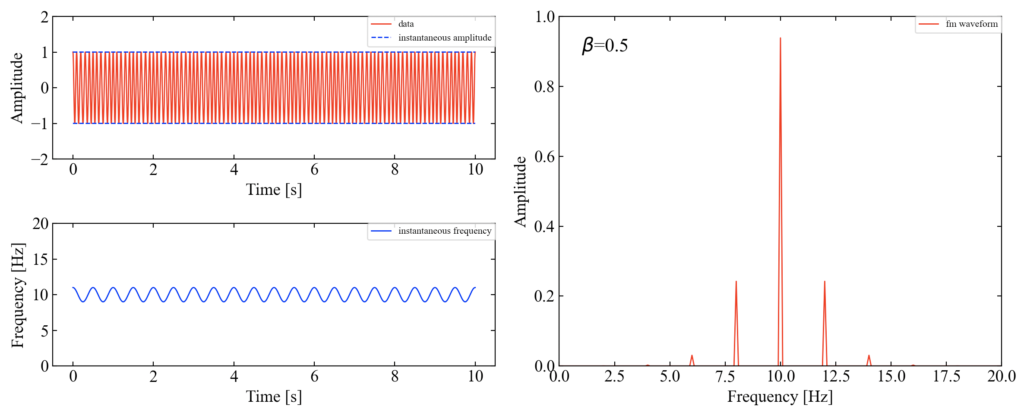
どうやら変調周波数がサイドバンドの間隔となるようです。今回はfm=1の時は1[Hz]刻み、fm=2の時は2[Hz]刻みでサイドバンドが発生していることまで確認しました。

$\beta=1$

$\beta=1$も同様にサイドバンドの発達と主次数の低下を確認。

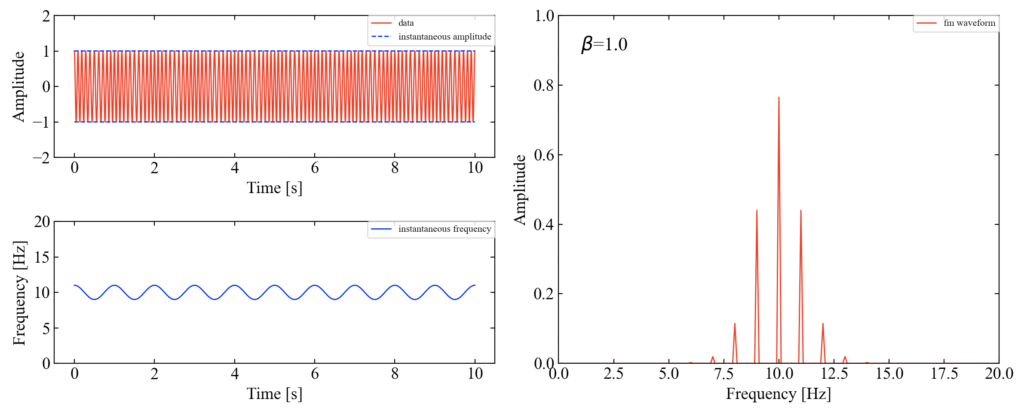
$\beta=1.5$

$\beta=1.5$付近で主次数と隣接サイドバンドの振幅がほぼ等しくなりました。

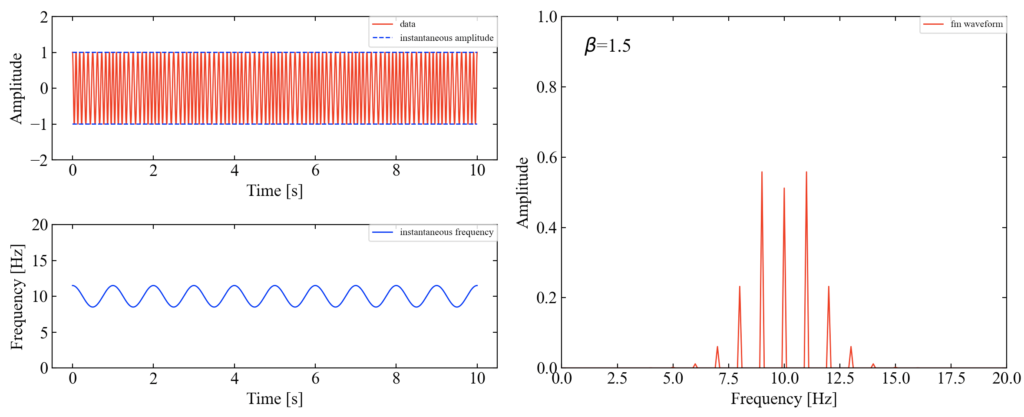
全次数の振幅は何で決定される？

静止画だと結局よくわからないので、動画を作ってみました。

こちらの動画は、変調指数$\beta$が一定で、変調周波数$f_{m}$を増加させていった挙動です。これは先ほど静止画で確認した通り、変調波同士で次数の振幅変化はなく、サイドバンドの間隔のみが変化する結果となりました。

（また、瞬時振幅や瞬時周波数が計算できないほどのパラメータになると挙動がおかしくなるようです）

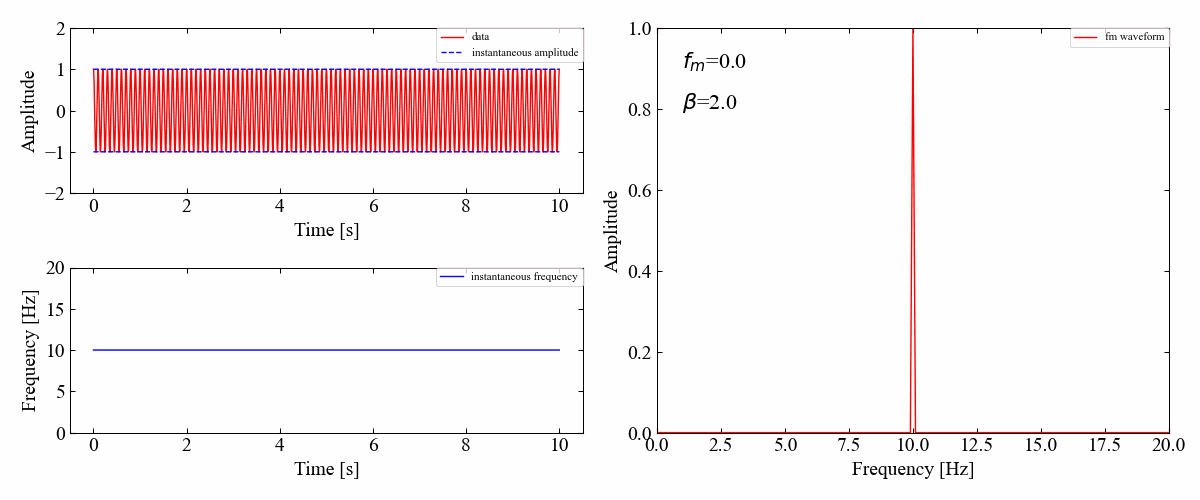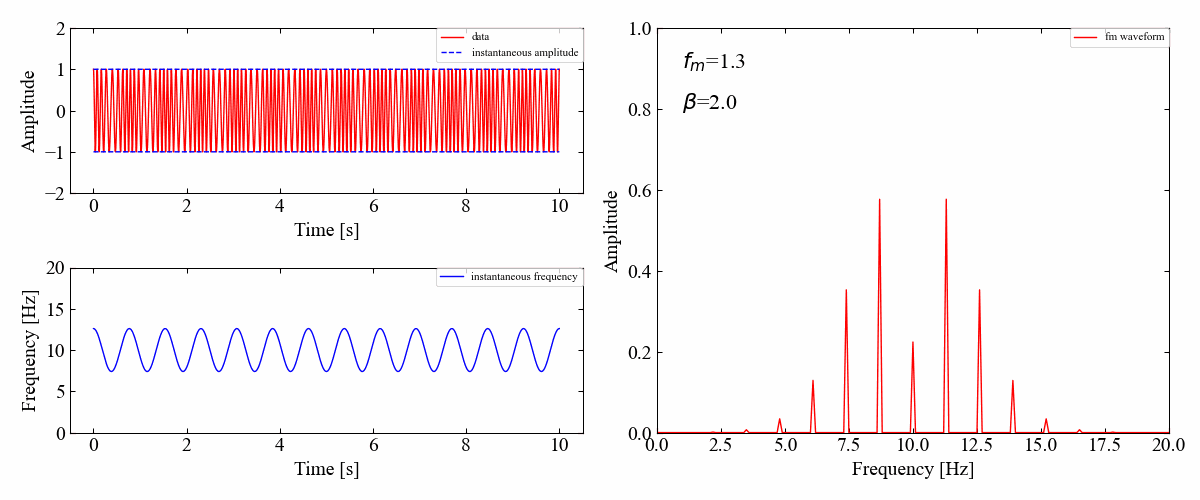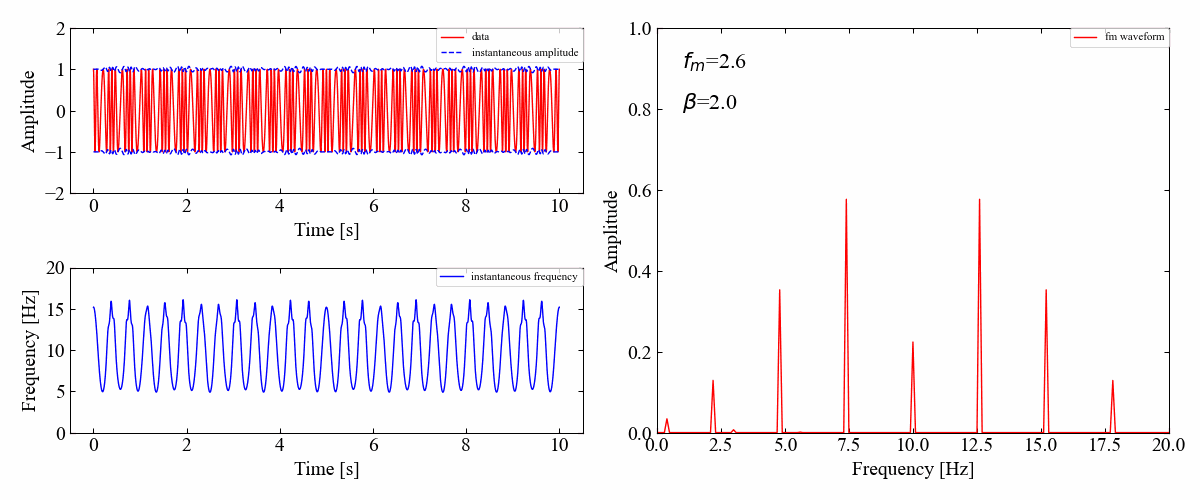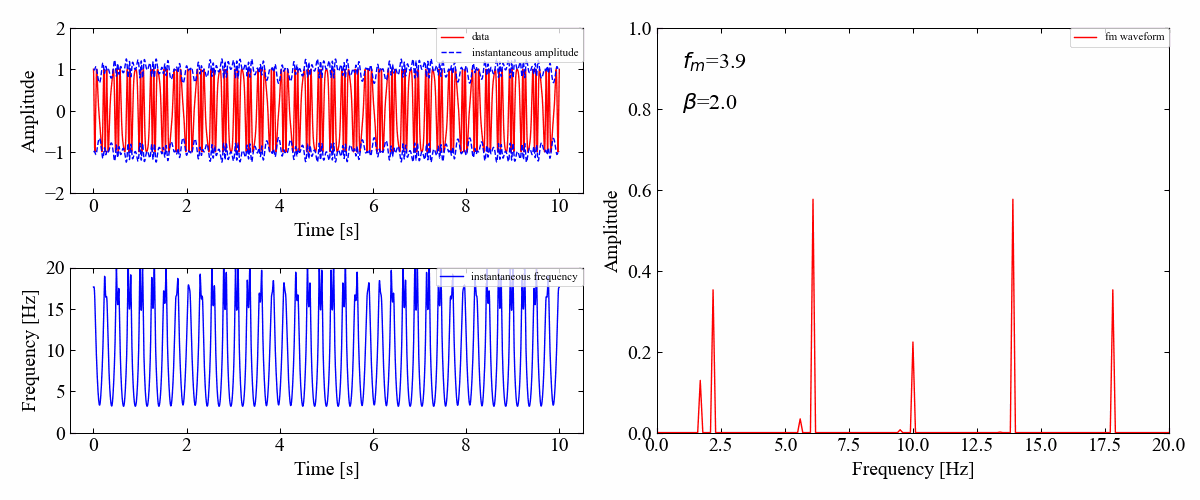
続いて変調周波数$f_{m}$が一定で、$\beta$を変動させた場合です。

どうやら全次数の振幅成分は$\beta$によって変化しますが、各サイドバンドの振幅は周期的に変化しているようです。

サイドバンドの法則は周波数変調の場合簡単に説明できないと上で書きましたが、そのことに関して以下の外部サイト様に詳細記載がありました。

周波数変調サイドバンド
任意の方法で任意のキャリアを変調すると、サイドバンドが生成されます。振幅変調信号の場合、これらの側波帯が作成される方法、およびその帯域幅と振幅は非常に簡単です。周波数変調信号の状況はかなり異なります。

FMサイドバンドは、偏差のレベルと変調の周波数の両方に依存します。実際、周波数変調信号の全スペクトルは、キャリアと、変調周波数の整数倍でキャリアの両側に広がる無限数の側波帯で構成されます。

この図から、偏差と変調周波数の値が変化すると、側波帯のレベルの値が上下することがわかります。

FM側波帯レベルの方程式と計算
FM信号内の側波帯の生成に関する幅広い原理を理解しておくことは非常に役立ちますが、数学的にレベルを決定する必要がある場合があります。
計算は、振幅変調信号の場合ほど簡単ではなく、いくつかの長い方程式を伴います。
中略
ベッセルの方程式を解いて個々の側波帯のレベルを決定することは非常に複雑になる可能性がありますが、コンピューターを使用した解法には理想的です。

数学を操作することにより、基本的なベッセル関数方程式を解いて、次の形式で表すことができます。周波数変調サイドバンドレベルの式シリーズが拡張された方法は、さまざまなサイドバンドがどのように生成され、それらが無限に拡張するかを示しています。
Fmuser:https://ja.fmuser.net/content/?6856.html

簡易的にはカーソンの法則を使うようですが、詳細な分析には第1種ベッセル関数を計算するそうです。振動を少し勉強した後なので自分でも計算できる…はず？（まだやらない）

まとめ

この記事では基本波、振幅変調波と共に周波数変調波の式とPythonコードによる分析コードを紹介しました。分析には瞬時振幅と瞬時周波数を計算できるヒルベルト変換を使いました。

周波数変調の波形はサイドバンドの間隔が変調周波数で決まることや、サイドバンドの振幅成分が変調指数で周期的に変化することも確認できました。

ただし、各パラメータによって周期が変化する振幅を正確に見積もろうとした場合は微分方程式を数値計算する必要があることもわかりました。

まずは波を描くことや分析できるようになったので今回はここでおしまいにしますが、機会があれば第1種ベッセル関数にも手を出してみようと思います（名前もかっこいいので）。

周波数変調の波形が自由に描けるようになりました！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！

Pythonで学ぶ周波数変調(FM)！変調式と特徴を見てみる

周波数変調波の概要

無変調波と振幅変調波の復習

基本波の式と例

振幅変調波の式と例

周波数変調波

周波数変調波の例

周波数変調の式

周波数変調は何に使われる？

通信技術

振動騒音技術

Pythonで周波数変調波を分析してみるコード

開発環境

参考知識

フーリエ変換

ヒルベルト変換

全コード

実行結果

\(\beta=0\)

\(\beta=0.5\)

\(\beta=1\)

\(\beta=1.5\)

全次数の振幅は何で決定される？

まとめ

コメントを残すコメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

周波数変調波の概要

無変調波と振幅変調波の復習

基本波の式と例

振幅変調波の式と例

周波数変調波

周波数変調波の例

周波数変調の式

周波数変調は何に使われる？

通信技術

振動騒音技術

Pythonで周波数変調波を分析してみるコード

開発環境

参考知識

フーリエ変換

ヒルベルト変換

全コード

実行結果

\(\beta=0\)

\(\beta=0.5\)

\(\beta=1\)

\(\beta=1.5\)

全次数の振幅は何で決定される？

まとめ

SNSでもご購読できます。

コメントを残す コメントをキャンセル

最近の投稿

アーカイブ

カテゴリー

コメントを残すコメントをキャンセル