
単一の応答曲面上を遺伝的アルゴリズムで探査するコードを書いたので、次はトレードオフ関係を持つ2つの応答曲面間の多目的最適化に挑戦します。ここではPyTorchによる応答曲面の作成からPlatypusによる多目的最適化、結果の可視化まで全てPythonで書いた内容を紹介します。
こんにちは。wat(@watlablog)です。ここでは機械学習によって得られた2つの応答曲面間で多目的最適化をやってみます!
応答曲面とは?
応答曲面とは、何かしらのシステム(シミュレーションモデルや実験)の応答値によって構築された曲面です。
設計変数を駆動させてシステムの応答を取り、すき間を補間してモデルを作成します。実現象が複雑な場合は応答曲面を作る事自体にも難しさがあります。
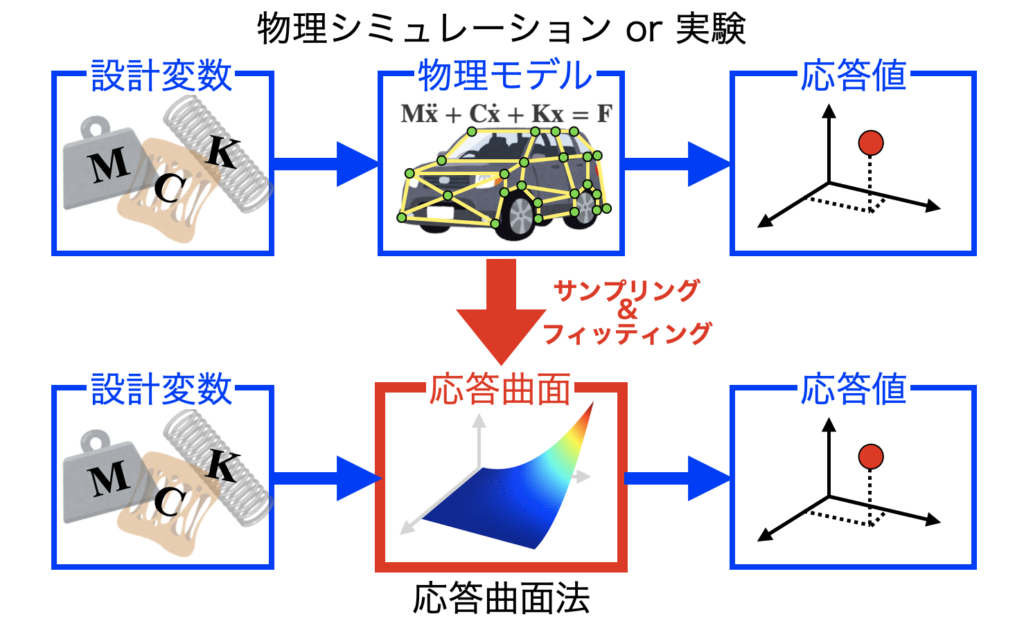
応答を得るには時間がかかるシステムでも一度事前に応答曲面を作っておけば、その後の探査が高速で実行できるというメリットがあります。
応答曲面の概要や単一の応答曲面上の最適化については「1つの応答曲面を遺伝的アルゴリズムで探査するPythonコード例」に詳細を記載しましたので、是非こちらの記事をご覧ください。
多目的最適化とは?
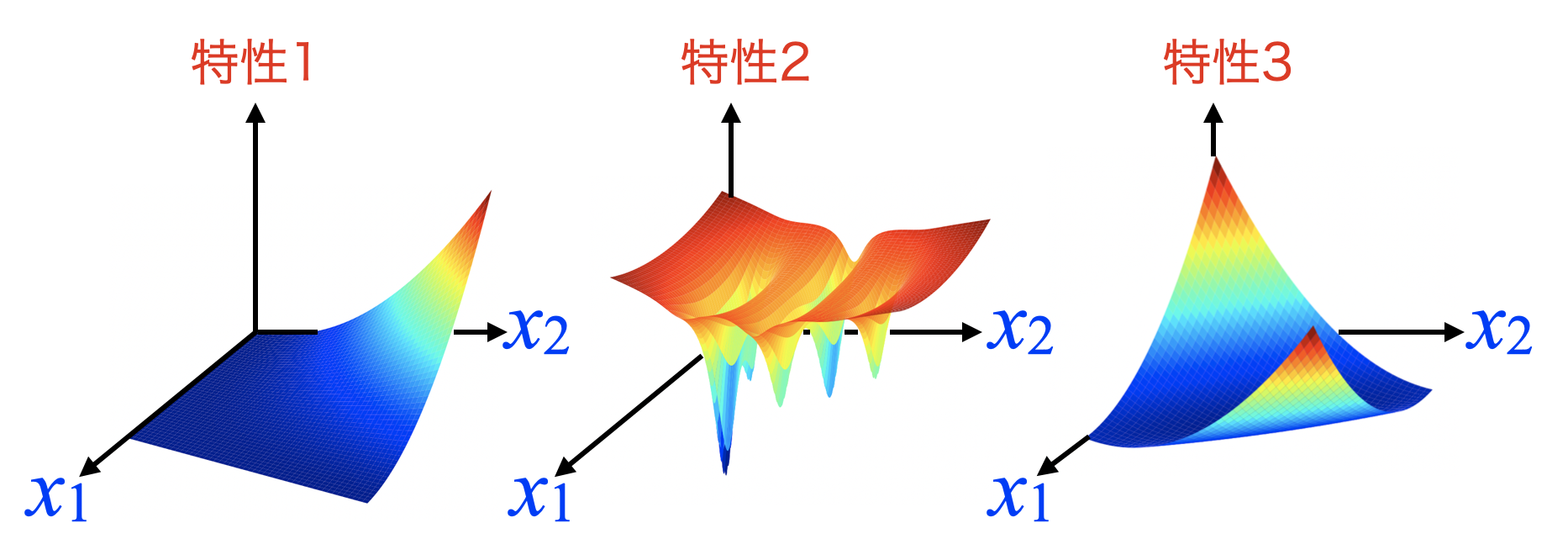
世の中は多目的最適化問題で溢れています。例えば以下の図は、設計変数\(x_{1}, x_{2}\)が取り得る範囲で特性値をプロットした例を示しています。
通常、何かを設計する時は単一の特性値だけを目的にするのではなく、複数の特性が同時に要件を満たすように調整を行います(性能、コスト、デザイン性…等)。
考慮する特性が多ければ多いほどその設計は難解な物になり、このような問題を最適化する事を多目的最適化と呼びます。
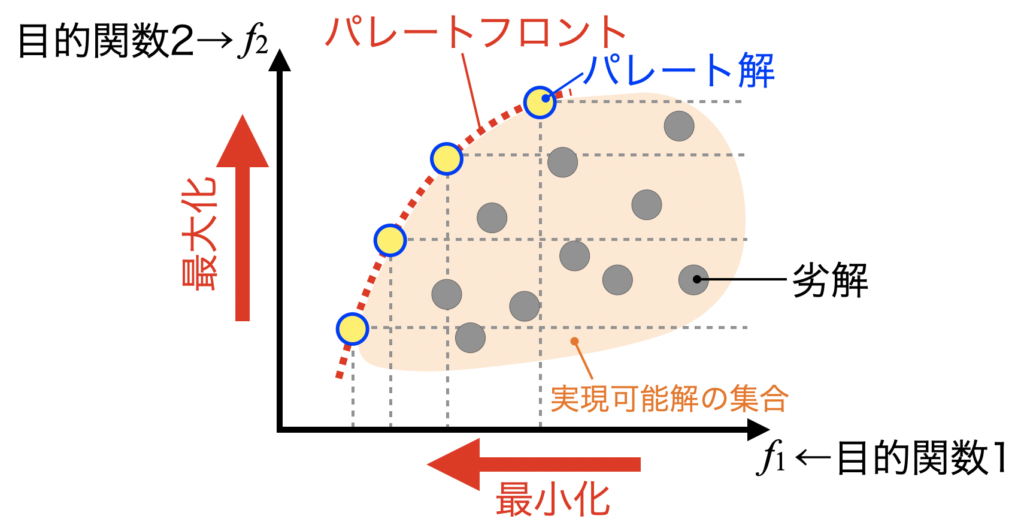
多目的最適化で複数の目的関数の最小化や最大化を行う事で、パレート解を得る事ができます。これらの用語は「Platypusで多目的最適化からパレートフロントを求める方法」で解説していますので、是非こちらも併せて参考にしてください。
複数の応答曲面間で多目的最適化を行うPythonコード
問題設定
ここでは2つの応答曲面を構築して多目的最適化を行います。
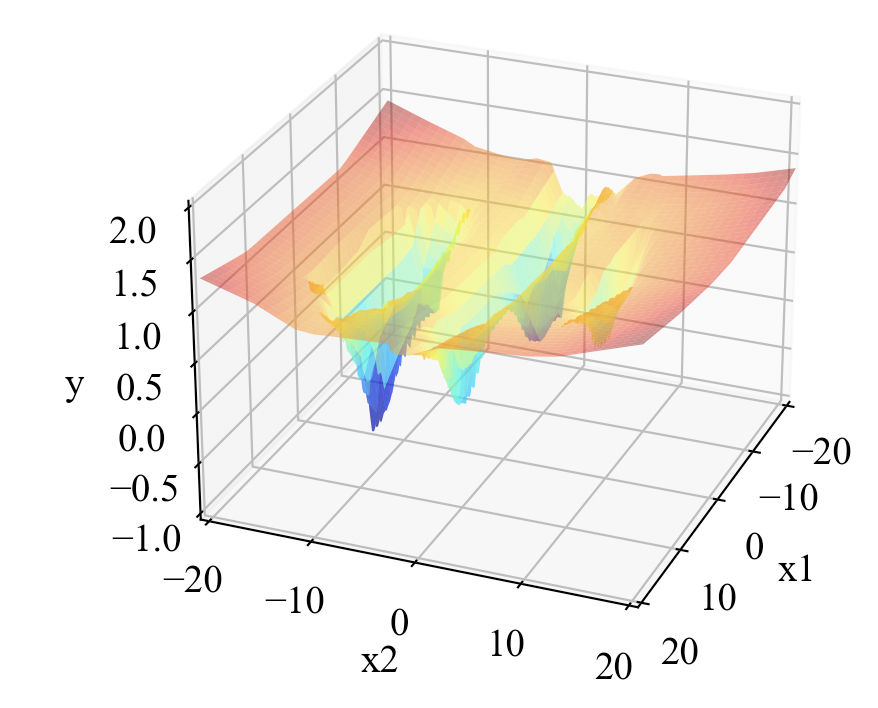
一つ目の関数は式(1)で示すFive-Well Potential Functionです。
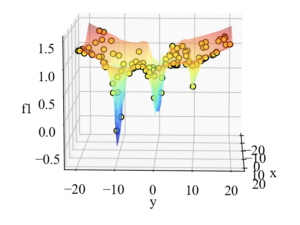
複雑な式の通り、以下のような多峰な形状をしています。
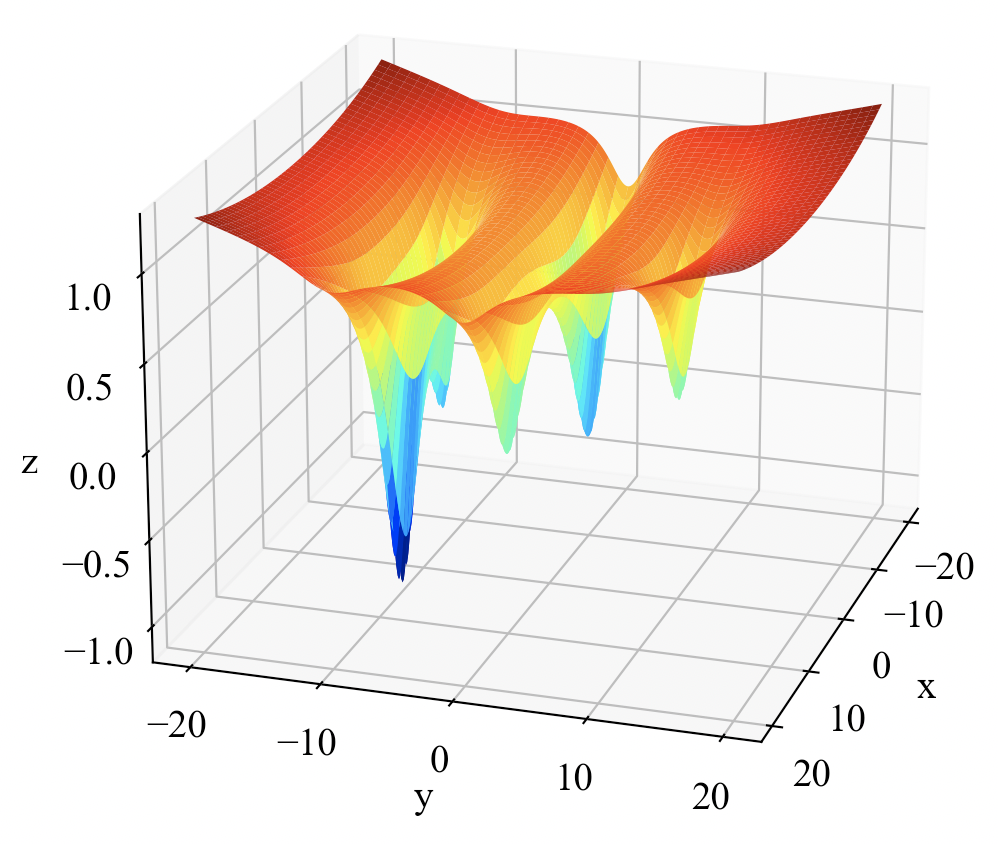
2つ目は式(2)に示すEggholder functionです。
こちらは絶対値とかも入っているからか、結構ギザギザ(コード間違ったかな?)。
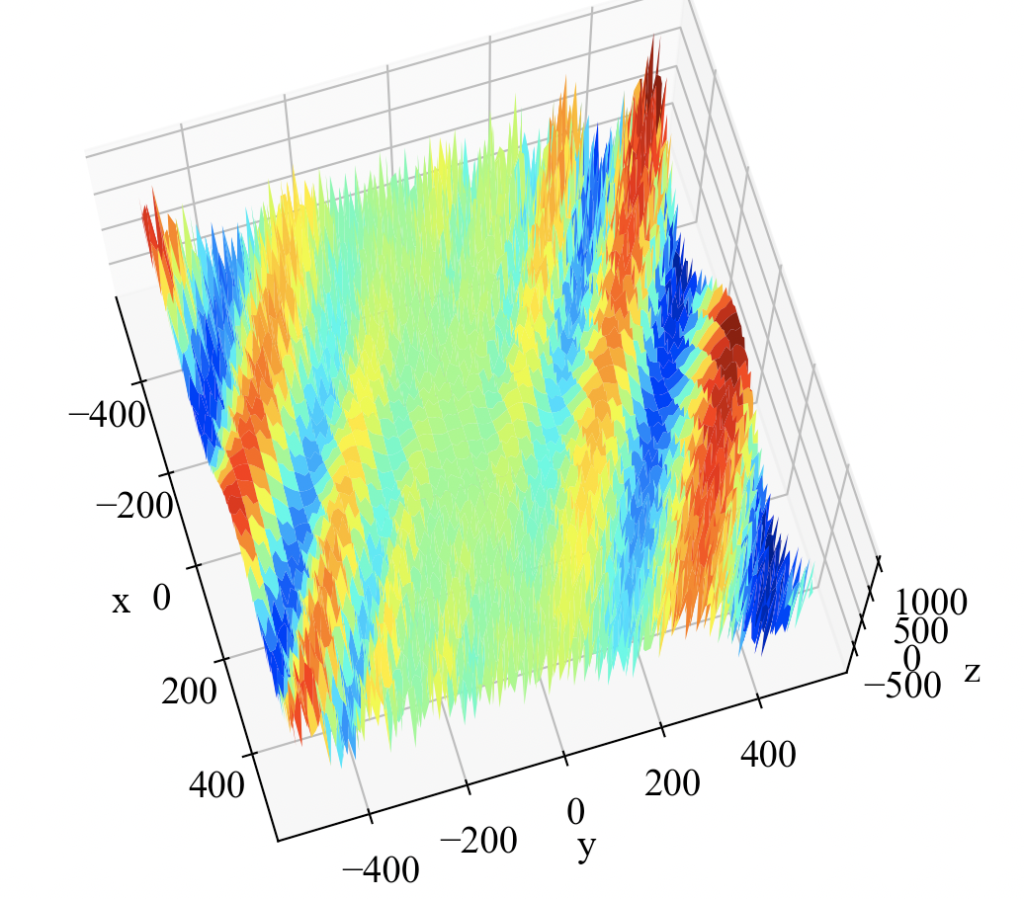
応答曲面モデルを作るコード(PyTorch)
これらの関数をただ多目的最適化にかけたい場合は、特に機械学習で回帰を行う必要もなく、単純に数式をモデルとして扱えば良いのですが、PyTorchとの連携を練習したいがためにあえてニューラルネットワークによるトレーニングを行います。
PyTorchによる学習モデルを使って探査ができるようになると、色々役立ちそうです。
Five-Well Potential functionのトレーニングコード
「PyTorchで色々な非線形関数を回帰してみたらすごかった」で紹介した方法を使って作成する回帰モデルを応答曲面モデルとしています。ここでは動画の作成も一緒にやっているので、ちょっと動作は遅いです。気になる方は動画作成部分を削除したりコメントアウトしたりする事をおすすめします。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 |
import torch from torch import nn, optim import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob import cloudpickle # GIFアニメーションを作成 def create_gif(in_dir, out_filename): # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) imgs = [] # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # 線形回帰ネットワークのclassをnn.Moduleの継承で定義 class Regression(nn.Module): # コンストラクタ(インスタンス生成時の初期化) def __init__(self): super().__init__() self.linear1 = nn.Linear(3, 32) self.linear2 = nn.Linear(32, 32) self.linear3 = nn.Linear(32, 16) self.linear4 = nn.Linear(16, 1) # メソッド(ネットワークをシーケンシャルに定義) def forward(self, x): x = nn.functional.relu(self.linear1(x)) x = nn.functional.relu(self.linear2(x)) x = nn.functional.relu(self.linear3(x)) x = self.linear4(x) return x # トレーニング関数 def train(model, optimizer, E, iteration, x, y): # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = model(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print('epoch=', i+1, 'loss=', loss) #グラフ描画用にXY軸とグリッドを作成 X1 = np.arange(-10, 11, 0.5) X2 = np.arange(-10, 11, 0.5) X, Y = np.meshgrid(X1, X2) # データをテンソルに変換(切片用の定数1も結合) X2 = torch.from_numpy(X.ravel().astype(np.float32)).float() Y2 = torch.from_numpy(Y.ravel().astype(np.float32)).float() Input = torch.stack([torch.ones(len(X.ravel())), X2, Y2], 1) # 100計算毎にプロットを保存 if (i + 1) % 100 == 0: Z = test(model, Input).reshape(X.shape) plot_3d(x.T[1], x.T[2], y, X, Y, Z, losses, 'out', i+1) return model, losses # テスト def test(model, x): y_pred = model(x).data.numpy() return y_pred # グラフ描画関数 def plot_3d(x1, x2, z, X, Y, Z, losses, dir, index): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(-20, 20) ax1.set_ylim(-20, 20) ax1.set_zlim(-1, 1) ax2.set_xlim(0, 10000) ax2.set_ylim(0.0001, 100) ax2.set_yscale('log') # データプロット ax1.scatter3D(x1, x2, z, label='dataset') ax1.plot_surface(X, Y, Z, cmap='jet') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses) - 1], color='red') ax2.text(600, 3, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 5, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend(bbox_to_anchor=(0, 1), loc='upper left') fig.tight_layout() # dirフォルダが無い時に新規作成 if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # plt.show() if index == 10000: plt.show() plt.close() plt.close() # ------------------------------------------------------------------- # トレーニングデータ x1 = np.random.uniform(-20, 20, 100) x2 = np.random.uniform(-20, 20, 100) grid_x, grid_y = np.meshgrid(x1, x2) # ノイズを含んだ平面点列データを作成 # Five-well potential function (https://qiita.com/tomitomi3/items/d4318bf7afbc1c835dda) z = ((1 - (1 / (1 + 0.05 * (grid_x ** 2) + (grid_y - 10) ** 2))) - (1 / ((1 + 0.05 * (grid_x - 10) ** 2) + grid_y ** 2)) - (1.5 / ((1 + 0.03 * (grid_x + 10) ** 2) + grid_y ** 2)) - (2 / ((1 + 0.05 * (grid_x - 5) ** 2) + (grid_y + 10) ** 2)) - (1 / ((1 + 0.1 * (grid_x + 5) ** 2) + (grid_y + 10) ** 2))) * (1 + 0.0001 * (grid_x ** 2 + grid_y ** 2) ** 1.2) # テンソル変換とデータ整形 grid_x = torch.from_numpy(grid_x.ravel().astype(np.float32)).float() grid_y = torch.from_numpy(grid_y.ravel().astype(np.float32)).float() z = torch.from_numpy(z.astype(np.float32)).float() X = torch.stack([torch.ones(len(grid_x)), grid_x, grid_y], 1) # ネットワークのインスタンスを生成 net = Regression() # 最適化アルゴリズム(RMSProp)と損失関数(MSE)を設定 optimizer = optim.RMSprop(net.parameters(), lr=0.01) E = nn.MSELoss() # トレーニング net, losses = train(model=net, optimizer=optimizer, E=E, iteration=10000, x=X, y=z) # ネットワークモデルをシリアライズしてファイルに保存 with open('model-A.pt', mode='wb') as f: cloudpickle.dump(net, f) # GIFアニメーションを作成する関数を実行する create_gif(in_dir='out', out_filename='movieA.gif') |
動画はこちら。10000iterationの学習をしています。
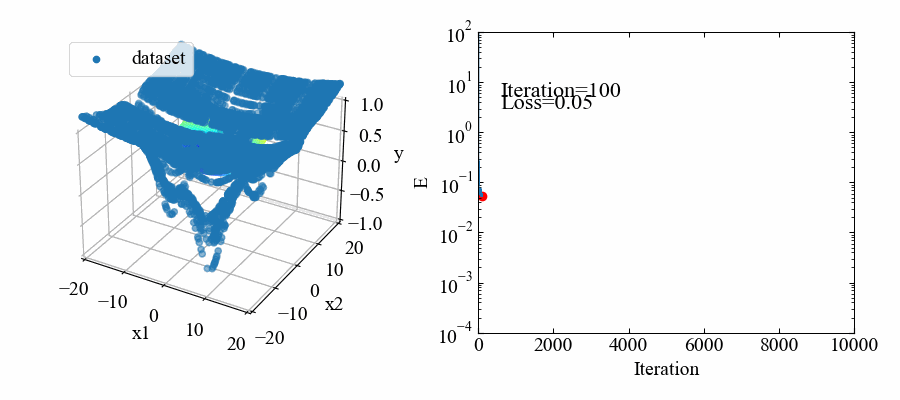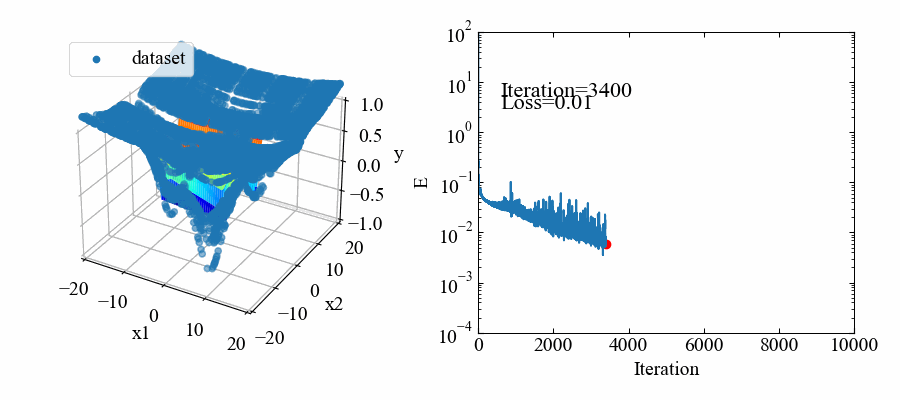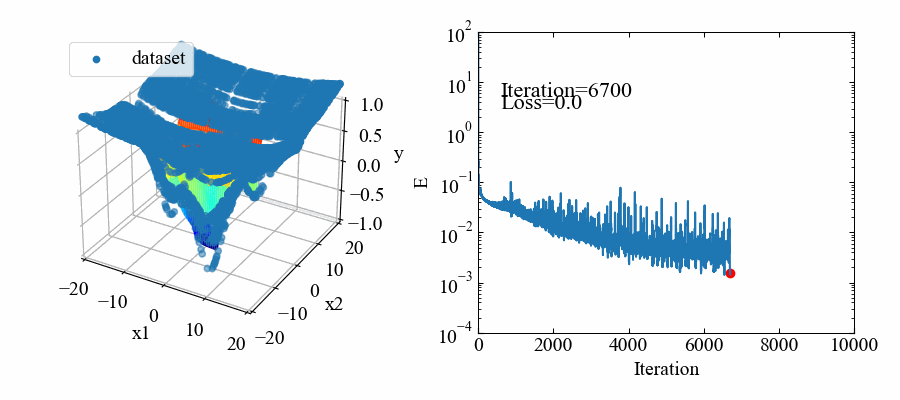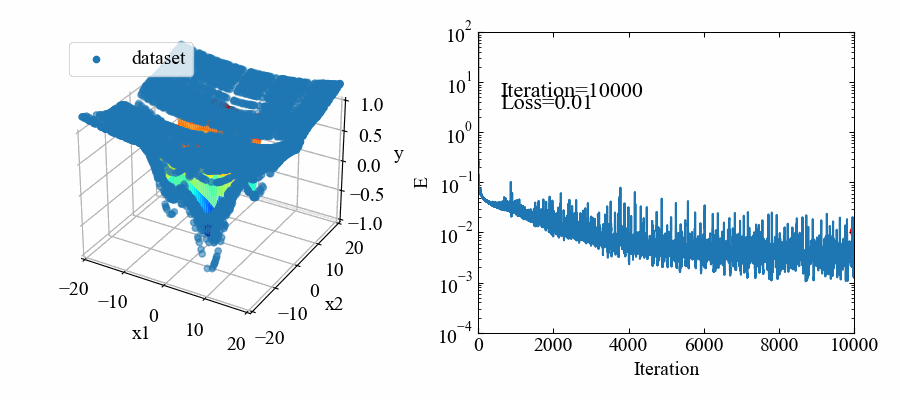
応答曲面モデルはmodel-A.ptというファイルで保存されます。
Eggholder functionのトレーニングコード
コードはほぼ同じですが、こちらの関数の方が複雑なため中間層の数を増やし、RMSPropの学習率も調整しています。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 |
import torch from torch import nn, optim import numpy as np from matplotlib import pyplot as plt from PIL import Image import os import glob import cloudpickle # GIFアニメーションを作成 def create_gif(in_dir, out_filename): # ファイルパスをソートしてリストする path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) imgs = [] # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) imgs.append(img) # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # 線形回帰ネットワークのclassをnn.Moduleの継承で定義 class Regression(nn.Module): # コンストラクタ(インスタンス生成時の初期化) def __init__(self): super().__init__() self.linear1 = nn.Linear(3, 32) self.linear2 = nn.Linear(32, 32) self.linear3 = nn.Linear(32, 32) self.linear4 = nn.Linear(32, 32) self.linear5 = nn.Linear(32, 16) self.linear6 = nn.Linear(16, 1) # メソッド(ネットワークをシーケンシャルに定義) def forward(self, x): x = nn.functional.relu(self.linear1(x)) x = nn.functional.relu(self.linear2(x)) x = nn.functional.relu(self.linear3(x)) x = nn.functional.relu(self.linear4(x)) x = nn.functional.relu(self.linear5(x)) x = self.linear6(x) return x # トレーニング関数 def train(model, optimizer, E, iteration, x, y): # 学習ループ losses = [] for i in range(iteration): optimizer.zero_grad() # 勾配情報を0に初期化 y_pred = model(x) # 予測 loss = E(y_pred.reshape(y.shape), y) # 損失を計算(shapeを揃える) loss.backward() # 勾配の計算 optimizer.step() # 勾配の更新 losses.append(loss.item()) # 損失値の蓄積 print('epoch=', i+1, 'loss=', loss) #グラフ描画用にXY軸とグリッドを作成 X1 = np.arange(-512, 512, 16) X2 = np.arange(-512, 512, 16) X, Y = np.meshgrid(X1, X2) # データをテンソルに変換(切片用の定数1も結合) X2 = torch.from_numpy(X.ravel().astype(np.float32)).float() Y2 = torch.from_numpy(Y.ravel().astype(np.float32)).float() Input = torch.stack([torch.ones(len(X.ravel())), X2, Y2], 1) # 100計算毎にプロットを保存 if (i + 1) % 100 == 0: Z = test(model, Input).reshape(X.shape) plot_3d(x.T[1], x.T[2], y, X, Y, Z, losses, 'out', i+1) return model, losses # テスト def test(model, x): y_pred = model(x).data.numpy() return y_pred # グラフ描画関数 def plot_3d(x1, x2, z, X, Y, Z, losses, dir, index): # ここからグラフ描画------------------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(9, 4)) ax1 = fig.add_subplot(121, projection='3d') ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(122) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x1') ax1.set_ylabel('x2') ax1.set_zlabel('y') ax2.set_xlabel('Iteration') ax2.set_ylabel('E') # スケール設定 ax1.set_xlim(-512, 512) ax1.set_ylim(-512, 512) ax1.set_zlim(-1000, 1000) ax2.set_xlim(0, 10000) ax2.set_ylim(1000, 100000) ax2.set_yscale('log') # データプロット ax1.scatter3D(x1, x2, z, label='dataset') ax1.plot_surface(X, Y, Z, cmap='jet') ax2.plot(np.arange(0, len(losses), 1), losses) ax2.scatter(len(losses), losses[len(losses) - 1], color='red') ax2.text(600, 3000, 'Loss=' + str(round(losses[len(losses)-1], 2)), fontsize=16) ax2.text(600, 8000, 'Iteration=' + str(round(len(losses), 1)), fontsize=16) # グラフを表示する。 ax1.legend(bbox_to_anchor=(0, 1), loc='upper left') fig.tight_layout() # dirフォルダが無い時に新規作成 if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(index)) + '.png']) # 画像を保存する plt.savefig(path) # plt.show() if index == 2000: plt.show() plt.close() plt.close() # ------------------------------------------------------------------- # トレーニングデータ x1 = np.random.uniform(-512, 512, 50) x2 = np.random.uniform(-512, 512, 50) grid_x, grid_y = np.meshgrid(x1, x2) # ノイズを含んだ平面点列データを作成 # Eggholder function (https://qiita.com/tomitomi3/items/d4318bf7afbc1c835dda) z = -(grid_y + 47) * np.sin(np.sqrt(np.abs(grid_y + (grid_x/2) + 47))) - grid_x * np.sin(np.abs(grid_x - (grid_y + 47))) # テンソル変換とデータ整形 grid_x = torch.from_numpy(grid_x.ravel().astype(np.float32)).float() grid_y = torch.from_numpy(grid_y.ravel().astype(np.float32)).float() z = torch.from_numpy(z.astype(np.float32)).float() X = torch.stack([torch.ones(len(grid_x)), grid_x, grid_y], 1) # ネットワークのインスタンスを生成 net = Regression() # 最適化アルゴリズム(RMSProp)と損失関数(MSE)を設定 optimizer = optim.RMSprop(net.parameters(), lr=0.005) E = nn.MSELoss() # トレーニング net, losses = train(model=net, optimizer=optimizer, E=E, iteration=10000, x=X, y=z) # ネットワークモデルをシリアライズしてファイルに保存 with open('model-B.pt', mode='wb') as f: cloudpickle.dump(net, f) # GIFアニメーションを作成する関数を実行する create_gif(in_dir='out', out_filename='movie-B.gif') |
以下が学習中の動画です。色々調整しましたがあまり誤差関数が低くなりませんね…。今回は凹凸があれば良いというレベルなのでこのまま使います(難しい!)。
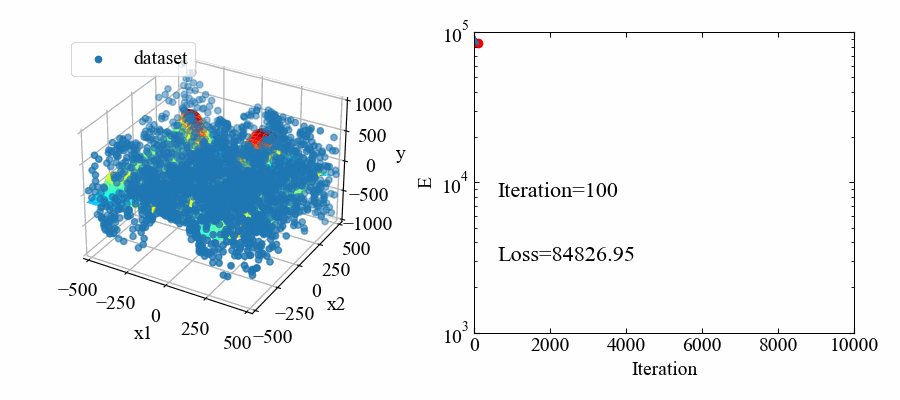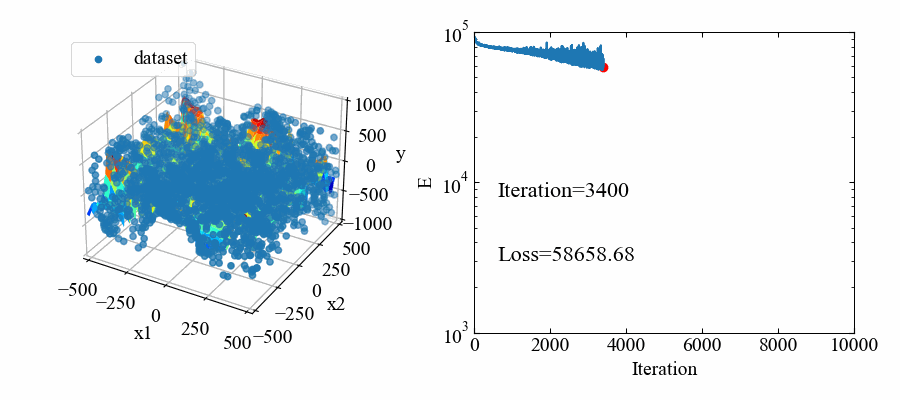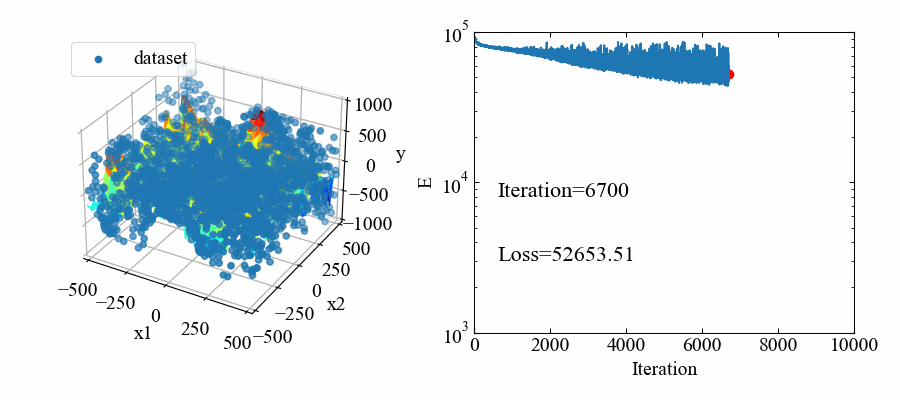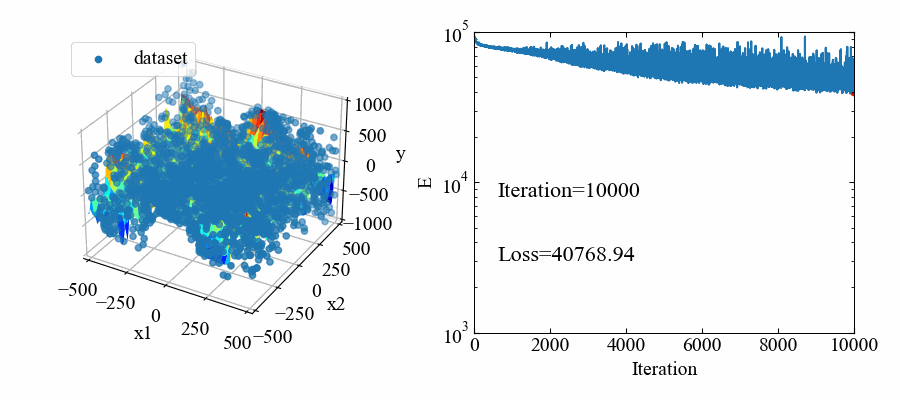
応答曲面はmodel-B.ptというファイルに保存されます。

多目的最適化を行うコード(Platypus)
以下が多目的最適化を行うコードです。「Platypusで多目的最適化からパレートフロントを求める方法」で紹介したコードで最適化問題の設定を行い、目的関数objectiveの部分で「1つの応答曲面を遺伝的アルゴリズムで探査するPythonコード例」で紹介したモデル記法を使っている構造です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 |
from platypus import NSGAII, Problem, Real, nondominated from matplotlib import pyplot as plt import cloudpickle import torch # 目的関数(ネットワークモデル×2) def objective(vars): x = vars[0] y = vars[1] x = torch.tensor(x).float() y = torch.tensor(y).float() Input = torch.stack([torch.tensor(1), x, y], 0) # ファイルからネットワークモデルをデシリアライズして読み込み with open('model-A.pt', mode='rb') as f: net_A = cloudpickle.load(f) with open('model-B.pt', mode='rb') as f: net_B = cloudpickle.load(f) # ネットワークモデルから応答を計算 f1 = net_A(Input).data.numpy() f2 = net_B(Input).data.numpy() return [f1, f2] # 最適化計算を実行する関数 def optimization(n_var, n_obj, vars, n_run): # 設計変数と目的関数の数を設定 problem = Problem(n_var, n_obj) # 最適化問題に最小化を設定 problem.directions[:] = Problem.MINIMIZE # 設計変数と目的関数を設定 problem.types[:] = vars problem.function = objective # 最適化アルゴリズムを設定して計算を実行する algorithm = NSGAII(problem) algorithm.run(n_run) return algorithm # 変数を設定する var1 = Real(-20., 20.) var2 = Real(-20., 20.) vars = [var1, var2] # 最適化計算を実行する algorithm = optimization(n_var=len(vars), n_obj=2, vars=vars, n_run=100) # ここからグラフ描画---------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # グラフの入れ物を用意する。 fig = plt.figure(figsize=(6, 5)) ax1 = fig.add_subplot(111) # 軸のラベルを設定する。 ax1.set_xlabel('Objective1') ax1.set_ylabel('Objective2') # 最適化結果から実現可能解をプロットする。 obj1 = [] obj2 = [] for solution in algorithm.result: obj1.append(solution.objectives[0]) obj2.append(solution.objectives[1]) ax1.scatter(obj1, obj2, color='gray', edgecolor='gray', label='Trial', alpha=0.5) # パレート解をプロットする。 n_dominated = nondominated(algorithm.result) # 非劣解を抽出する obj1 = [] obj2 = [] for solution in n_dominated: obj1.append(solution.objectives[0]) obj2.append(solution.objectives[1]) ax1.scatter(obj1, obj2, color='yellow', edgecolor='black', label='Pareto solution') ax1.legend() # グラフを表示する。 plt.show() plt.close() |
以下は目的関数1(Five-Well Potential function)を横軸、目的関数2(Eggholder function)を縦軸にとった時の実現可能解(グレー)とパレート解(黄)をプロットした結果です。一応解が出てきました。
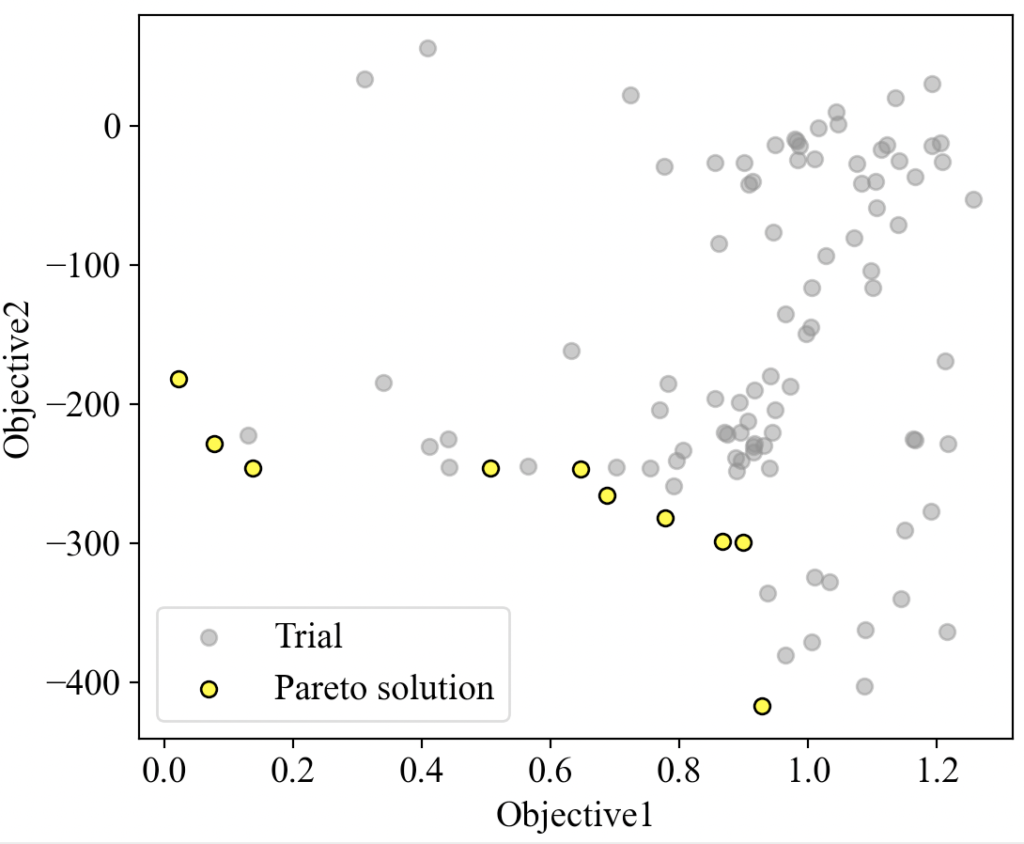
まとめ
この記事ではこれまで学んだニューラルネットワークによる回帰モデル生成、モデルのファイル保存と読み出し、遺伝的アルゴリズムによる多目的最適化、パレート解のプロット…を総動員した内容になりました(ちょっとごちゃごちゃした内容になってしまいました💦)。
ここまでの内容で、データ点からモデルを作ってその曲面上を探査する方法は大分わかってきたのではないかと思います。
本日はモデル生成、最小値探査、プロットと一連の応用記事となりました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!