
ベジェ曲線はコンピュータグラフィックスの分野で曲線を描く時によく使われています。描画に使う数式を理解して自分で実装する事ができれば、自動作図や画像処理の幅が広がります。ここではベジェ曲線の数式を解説しながらPythonコードを紹介します。
こんにちは。wat(@watlablog)です。ここでは制御点を使って曲線を描くベジェ曲線をPythonで描いてみます!
ベジェ曲線の概要
ベジェ曲線とは?
ベジェ曲線(Bezie curve)とは、フランスの自動車メーカであるシトロエン社のド・カステリョ氏と、同じく自動車メーカであるルノー社のピエール・ベジェ\(^{※}\)氏により独立に考案された曲線です。
※発音はベジェよりもベジエの方が近いかも。
ベジェ曲線はN個の制御点から作られる曲線です。まずはベジェ曲線の例として下図を見てみましょう。下図は3つの制御点で構築されたベジェ曲線を示しています。
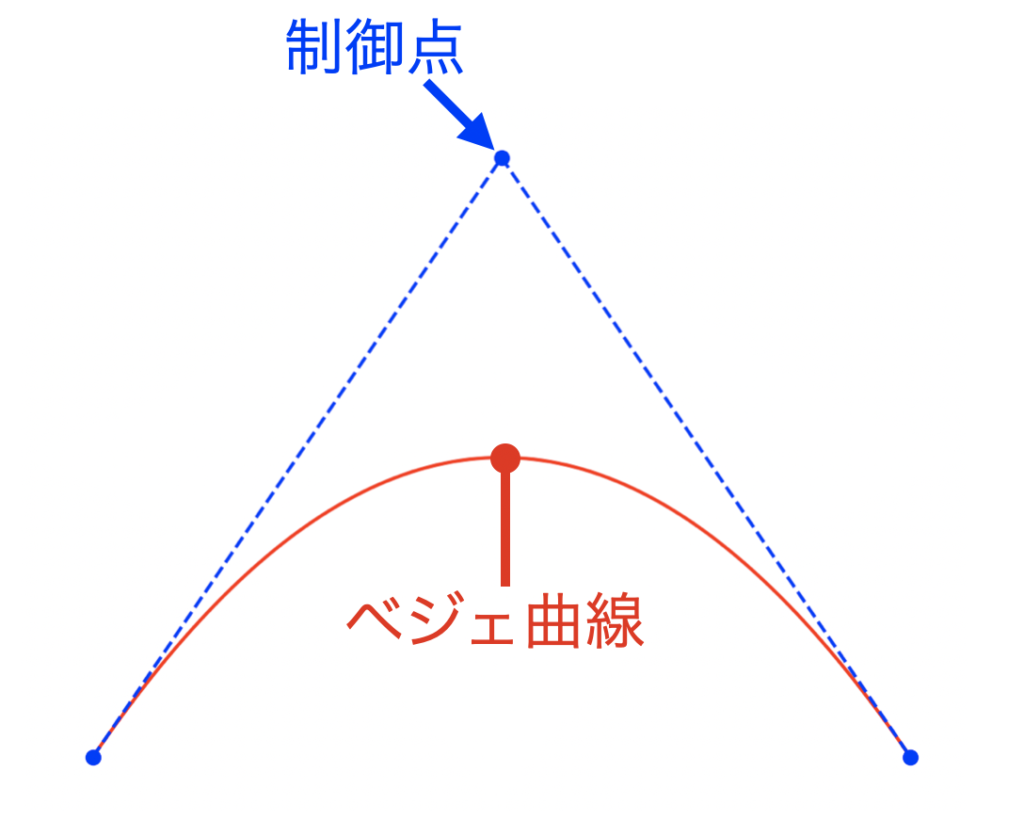
一見すると何の変哲も無い放物線のように見えますが、以下に示す特徴を持ちます。
特徴
曲線が常に制御点の凸包内にある
ベジェ曲線は「常に制御点の凸包(Convex hull)内に存在する」という特徴を持ちます。
凸包というのはなかなか聞かない単語と思いますが、制御点同士を繋いだ線の事です。
上記特徴は下図のように制御点が複数あったとしても、その制御点同士を繋いだ線の外にはベジェ曲線は出ないという意味です。
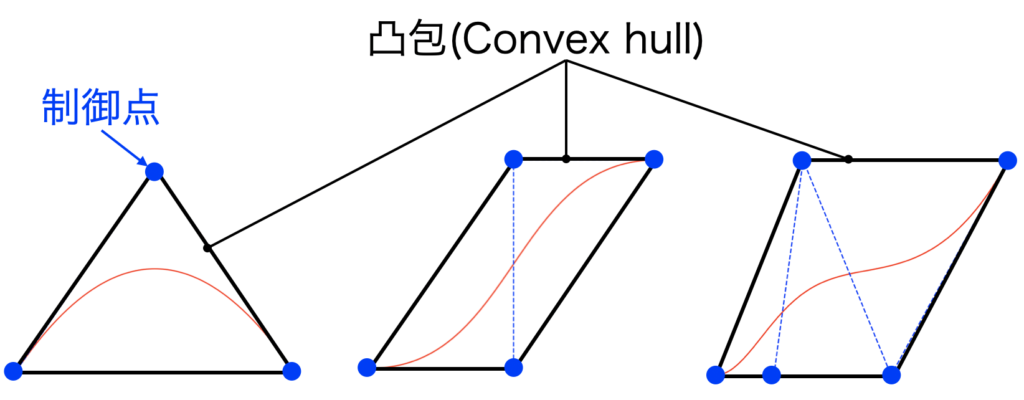
制御点を用いて曲線を描く方式には、ある意味多項式近似も当てはまりますが、多項式近似は凸包を出ないという制約には当てはまりません。制御点によっては思いもよらない曲線になる事があります。
ベジェ曲線はこの特徴のため制御しやすいとも言えます。曲線が交差したり、思ったより範囲外に曲線ができたりすると、自動作図の現場では中々扱いづらいです。
曲線は始点と終点を必ず通り、全ての制御点は通らない
ベジェ曲線は「始点と終点を必ず通り、全ての制御点は通らない」という特徴もまた持ちます。
多項式近似は最小二乗法により全ての点との誤差が最小になるようなフィッティングがされますが、これは全ての制御点を厳密には通らない事を意味します。
ベジェ曲線の場合は指定した始点と終点は必ず通るので、複数の曲線を組み合わせて形状を表現する場合に適しています。
但し、ベジェ曲線は全ての点を通るのではなく制御点により構成された直線群から曲線が接線連続になるように描かれます。これは中々言葉だけでは理解できないと思うので、以下にイメージを伝えるための動画を作成しました。
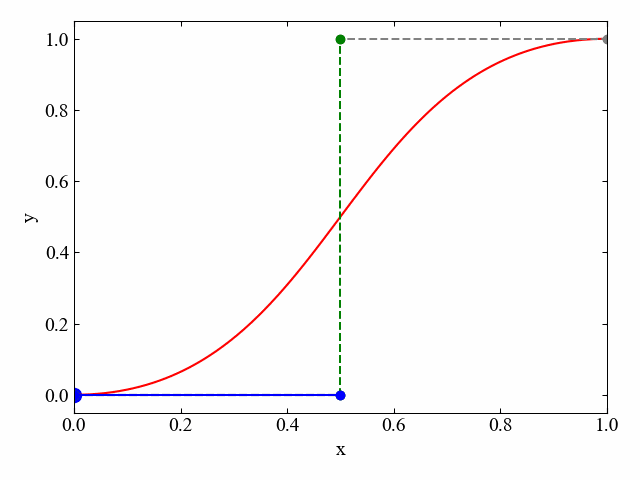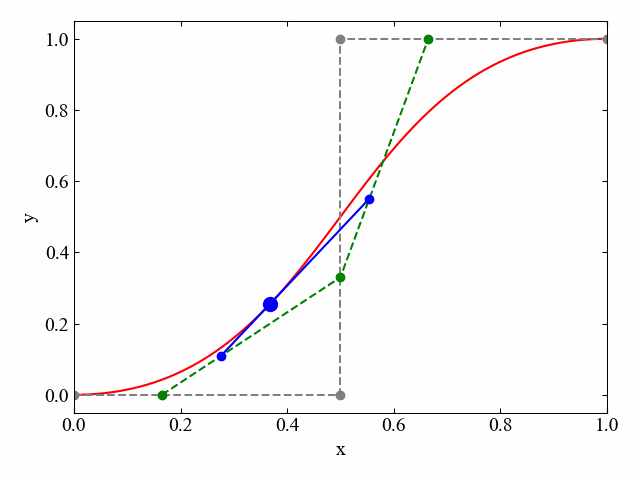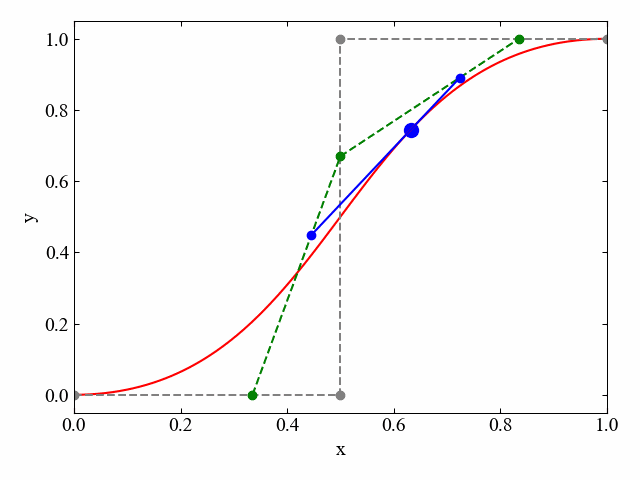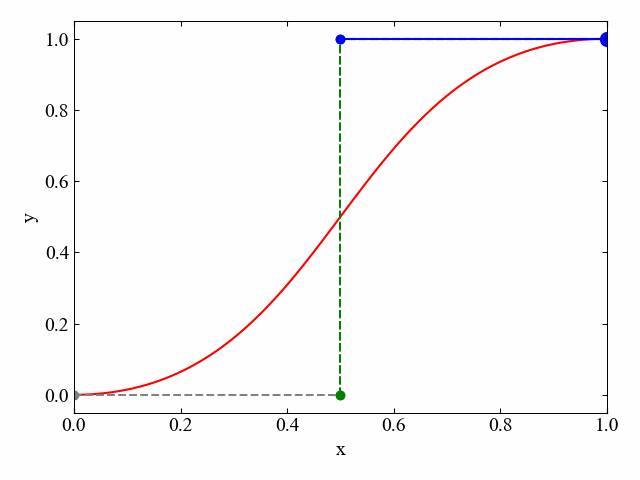
下図は3つの制御点により構成されたベジェ曲線(赤線)です。各制御点間で引かれた直線(灰色線)の内部を進行する移動点(緑点)により移動する直線(緑線)が作られます。
そして、その移動する直線の中をさらに移動する点(青点)の軌跡がベジェ曲線です。

制御点4つの場合は以下動画に示す通りです。制御点が増えた場合も、最終的に直線(ここでは青線)となるまでこの移動点操作を繰り返していく事で、ルール化された接線による曲線の描画が可能となります。
参考までに、制御点4つの場合の別の例を以下に示します。制御点が5つになるとさらに青線が折れ曲がり、青線内部を移動する点により構成される直線が接線となります。
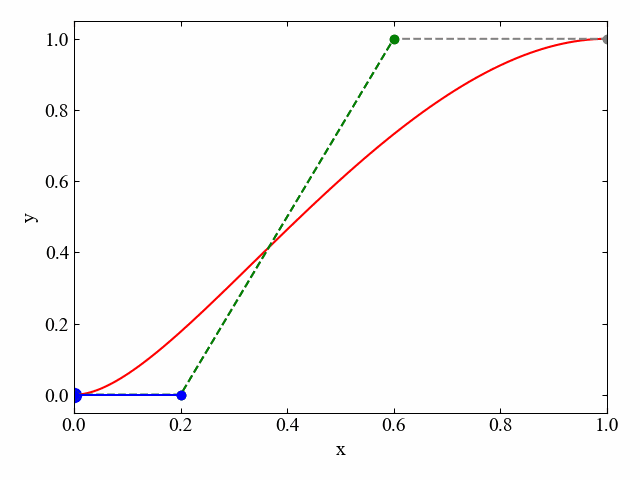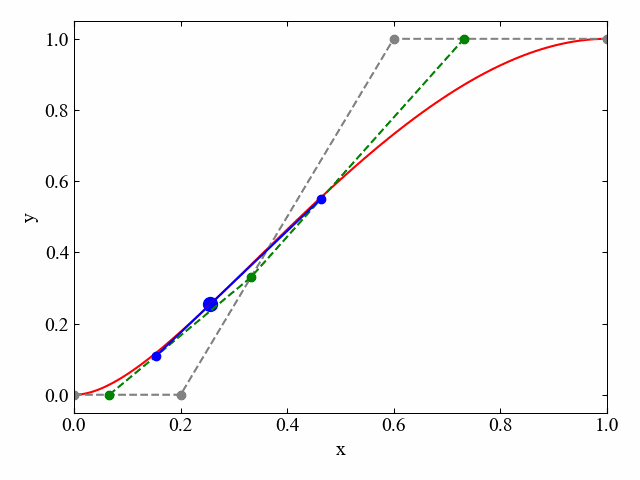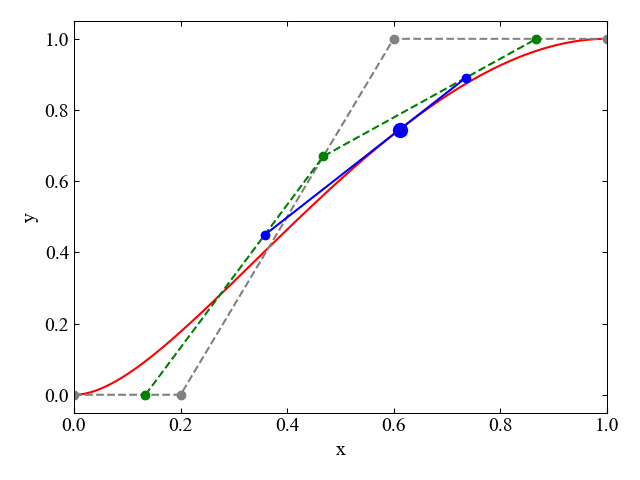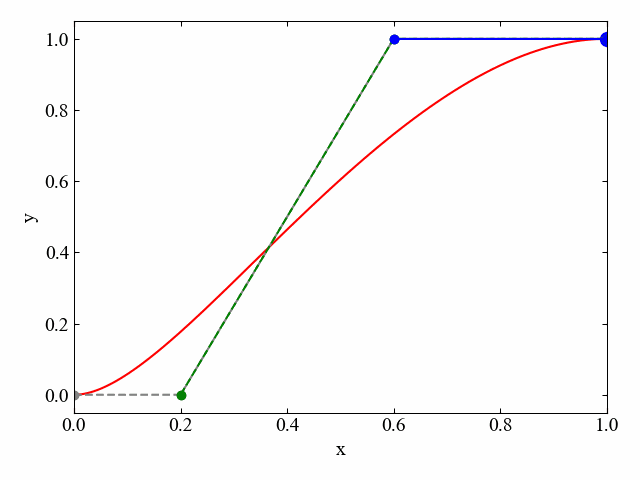
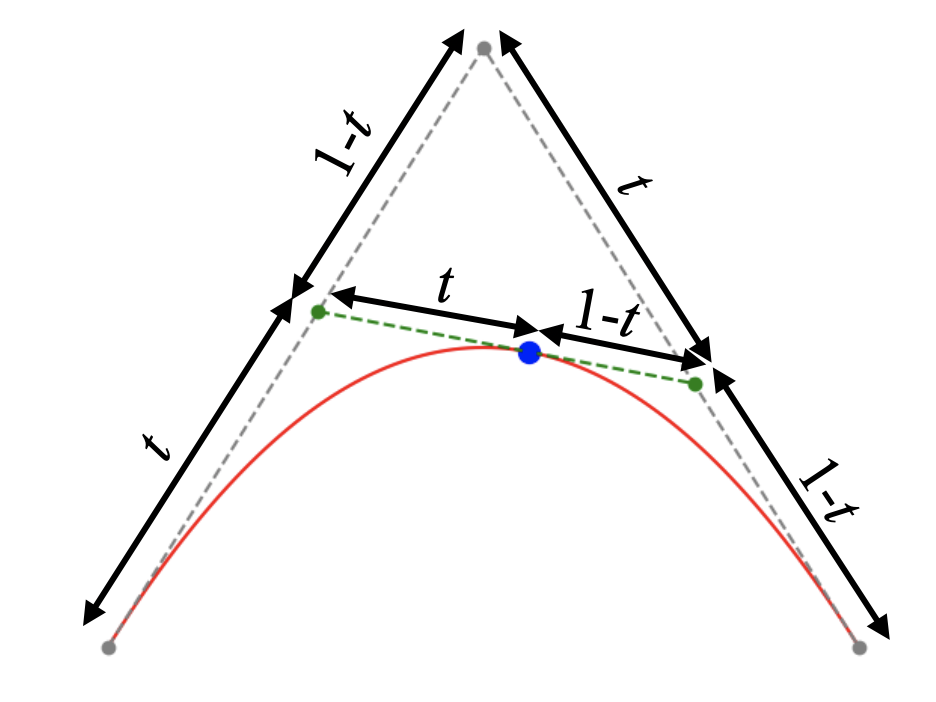
直線内を移動する点は常に\(t:1-t\)の比になります。このような各直線の全長を1として\(0\leq t \leq 1\)で変化する一般化パラメータ\(t\)を用いた直線分割手法をド・カステリョのアルゴリズムと呼びます。
※シトロエン社のカステリョ氏の方が最初に研究していたけど、論文公知はルノー社のベジェ氏が先だったので曲線名はベジェらしい(wiki情報ですが)。
イメトレはこんな所にして、続いて実践トレーニングをしてみましょう。
様々な曲線(自動車のデザインやフォント等)に使われる制御しやすい曲線を描くベジェ曲線をこれから学んでいきます!
ベジェ曲線を描くPythonコード
動作環境
この記事で動作確認した環境を以下にメモっておきます。
PC
| Windows | OS | Windows10 64bit |
|---|---|---|
| CPU | Intel 11th Core i7-11800H:2.3[GHz] | |
| メモリ | 16[GB] |
| Mac | OS | macOS Catalina 10.15.7 |
|---|---|---|
| CPU | 1.4[GHz] | |
| メモリ | 8[GB] |
Python環境
| Python | Python 3.9.6 |
|---|---|
| PyCharm (IDE) | PyCharm CE 2020.1 |
| Numpy | 1.21.1 |
| matplotlib | 3.4.3 |
指定した制御点で描画を練習するコード
厳密な定義を説明する前に、まずは簡単な事例でベジェ曲線のイメージを掴んでみましょう。この記事では理論的に曲線の描き方を説明せず、答えのある状態から逆説的に式の意味を理解する程度に留めます。
2つの制御点
ベジェ曲線を2つの制御点で描く方法を説明します。
2点の場合のベジェ曲線は式(1)で書く事が可能です。
\(P(t)\)は\(0 \leq t \leq 1\)の範囲で描かれるベジェ曲線です。\(\mathbf{q}_{i}\)は制御点の座標を表すベクトル量であり\(\mathbf{q}_{i}=[x_{i}, y_{i}]^{\top}\)の形式で与えられます。2点の場合は非常に簡単な式ですが、まずは描いてみましょう。
Pythonで2点のベジェ曲線を描くコードは以下です。上式をx, y成分それぞれで描いているだけなので説明は不要でしょう。コードはかなり愚直で無駄がありますが、とりあえず書いてみたという物です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 |
import numpy as np from matplotlib import pyplot as plt # 2点のベジェ曲線を描く関数 def bezier_curve(): # 点の座標 q1 = [0., 0.] q2 = [0.5, 1.] Q = [q1, q2] px = [] py = [] t = np.arange(0, 1, 0.01) for i in range(len(t)): P = np.dot((1 - t[i]), Q[0]) + np.dot(t[i], Q[1]) px.append(P[0]) py.append(P[1]) return px, py, Q px, py, Q = bezier_curve() # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(0, 1) # データプロット ax1.plot(px, py, color='red', label='Bezie curve') qx = [] qy = [] for i in range(len(Q)): qx.append(Q[i][0]) qy.append(Q[i][1]) ax1.scatter(qx, qy, color='blue', label='Control point') ax1.legend() # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
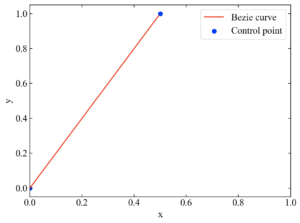
2つの制御点の場合のべシェ曲線は以下です。2点の場合は直線になります。
まだ感覚は掴めないと思いますので、続いて制御点が3点の場合を見てみましょう。
3つの制御点
制御点が3点の場合は式(2)で描く事ができます。何やら項が増えていますが、ここでもまずは描いてみる事を優先してみます。
ちなみにコードは以下です。グラフ部分は共通なので、関数部分のみ示します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 |
# 3点のベジェ曲線を描く関数 def bezier_curve(): # 点の座標 q1 = [0., 0.] q2 = [0.5, 1.] q3 = [1., 0.] Q = [q1, q2, q3] px = [] py = [] t = np.arange(0, 1, 0.01) for i in range(len(t)): P = np.dot((1 - t[i]) ** 2, Q[0]) + np.dot(2 * (1 - t[i]) * t[i], Q[1]) + np.dot(t[i] ** 2, Q[2]) px.append(P[0]) py.append(P[1]) return px, py, Q |
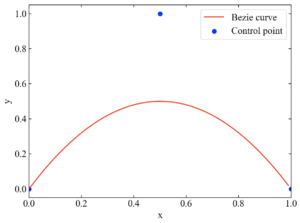
以下が結果です。制御点が3つだと曲線になる事がわかりました。
4つの制御点
くどいですが4つの制御点の場合は式(3)になります。カンの良い人なら既に法則に気付いているかも知れませんが、まずは結果を見てみましょう。
ちなみにちなみにコードは以下です。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
# 4点のベジェ曲線を描く関数 def bezier_curve(): # 点の座標 q1 = [0., 0.] q2 = [0.25, 1.] q3 = [0.75, 1.] q4 = [1., 0.] Q = [q1, q2, q3, q4] px = [] py = [] t = np.arange(0, 1, 0.01) for i in range(len(t)): P = np.dot((1 - t[i]) ** 3, Q[0]) + np.dot(3 * (1 - t[i]) ** 2 * t[i], Q[1]) + np.dot(3 * (1 - t[i]) * t[i] ** 2, Q[2]) + np.dot(t[i] ** 3, Q[3]) px.append(P[0]) py.append(P[1]) return px, py, Q |
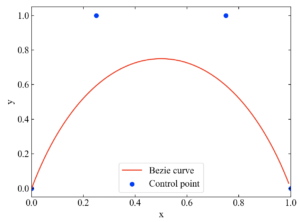
4点の場合は以下の結果を得ます。
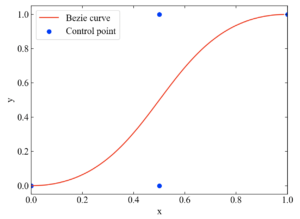
さらにちなみに、4点の座標を変更すると以下のようになります。
|
1 2 3 4 5 6 |
# 点の座標 q1 = [0., 0.] q2 = [0.5, 0.] q3 = [0.5, 1.] q4 = [1., 1.] Q = [q1, q2, q3, q4] |
ここまでは指定した点数でベジェ曲線を描く式とPythonコードを紹介しましたが、これではベジェ曲線を完全に理解したとは言えません。
ここからはベジェ曲線をどうやって一般的に描くかを調べた結果を紹介します。
任意制御点で一般化したベジェ曲線を描くコード
二項係数とパスカルの三角形
ベジェ曲線を描くコードを紹介する前に、事前知識として必要な二項係数(Binomial coefficients)を紹介します。
二項係数とは、二項展開の係数として現れる係数の事で、次式で示されます。
特に左辺は独特な形をしていますが、これはベクトルではありません。
この式は「整数\(n\)に対して、\(k\)を0から\(n\)まで代入して得られる値」を並べると有名なパスカルの三角形が現れます。
以下コードは二項係数を利用してパスカルの三角形を計算するコードです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 |
import numpy as np import math # 二項係数を計算する関数 def binomial_coefficient(n, k): nCk = math.factorial(n) / (math.factorial(k) * math.factorial(n - k)) return nCk # パスカルの三角形を作る関数 def pascal_triangle(N): triangle = np.zeros([N, N]) for n in range(N): for k in range(n + 1): triangle[n, k] = binomial_coefficient(n, k) print(triangle) pascal_triangle(10) |
以下が結果です。「1→1,1→1,2,1→1,3,3,1…」と特徴的な整数が並びます。この並び自体数学的に面白い性質があります。
詳しくは「外部サイト:パスカルの三角形の不思議な性質7個。パスカルの三角形に秘められた不思議な性質」にわかりやすく書いてあるので丸投げしてしまいますが、組み合わせの性質、n乗やべき乗の性質といった様々な数列が隠れている三角形です。
|
1 2 3 4 5 6 7 8 9 10 |
[[ 1. 0. 0. 0. 0. 0. 0. 0. 0. 0.] [ 1. 1. 0. 0. 0. 0. 0. 0. 0. 0.] [ 1. 2. 1. 0. 0. 0. 0. 0. 0. 0.] [ 1. 3. 3. 1. 0. 0. 0. 0. 0. 0.] [ 1. 4. 6. 4. 1. 0. 0. 0. 0. 0.] [ 1. 5. 10. 10. 5. 1. 0. 0. 0. 0.] [ 1. 6. 15. 20. 15. 6. 1. 0. 0. 0.] [ 1. 7. 21. 35. 35. 21. 7. 1. 0. 0.] [ 1. 8. 28. 56. 70. 56. 28. 8. 1. 0.] [ 1. 9. 36. 84. 126. 126. 84. 36. 9. 1.]] |
Bernstein多項式を使った一般式
ベジェ曲線は上で紹介した二項係数の性質を利用します。先ほど紹介した式(1)-(3)を、少し冗長ですが隠れている記号や乗数も表現して式(4)と書き下してみます。
すると各項は共通の因子を持ち、その係数や乗数に規則性がある事がわかります(下図)。
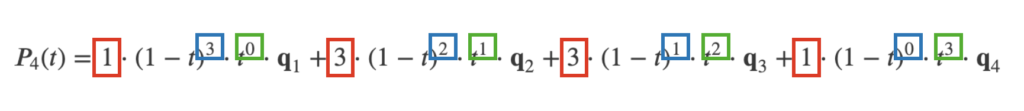
この図で赤枠で示した部分が二項係数の数列になっている事に気付く事で、以下の一般式(5)を得ます。
式(5)における\(B_{k}^{n}\)はバーンスタイン多項式(Bernstein polynomial)と呼ばれ、二項係数を含むバーンスタイン多項式(さらに3次元等に拡張されると一般化されてバーンスタイン行列と呼ばれるらしい)と制御点座標ベクトル\(\mathbf{q}_{i}\)との積の総和がベジェ曲線となります。
ベジェ曲線を描くコード
前置きはかなり長くなってしまいましたが、以下がベジェ曲線を描くコードです。コピペ動作すると思います。
bezie_curve()関数に制御点をまとめたQを引数として渡して実行しています。Qのそれぞれの座標値や点の数を変化させる事で任意のベジェ曲線が描ける…はずです。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 |
import numpy as np import math from matplotlib import pyplot as plt # Bernstein多項式を計算する関数 def bernstein(n, t): B = [] for k in range(n + 1): # 二項係数を計算してからBernstein多項式を計算 nCk = math.factorial(n) / (math.factorial(k) * math.factorial(n - k)) B.append(nCk * t ** k * (1 - t) ** (n - k)) print(nCk, k, n-k) return B # ベジェ曲線を描く関数 def bezie_curve(Q): n = len(Q) - 1 dt = 0.01 t = np.arange(0, 1 + dt, dt) B = bernstein(n, t) px = 0 py = 0 for i in range(len(Q)): px += np.dot(B[i], Q[i][0]) py += np.dot(B[i], Q[i][1]) return px, py # 点座標を準備 q1 = [0., 0.] q2 = [0.5, 1.] q3 = [1., 0.] Q = [q1, q2, q3] #q1 = [0., 0.] #q2 = [0.5, 0.] #q3 = [0.5, 1.] #q4 = [1., 1.] #Q = [q1, q2, q3, q4] # ベジェ曲線を描く関数を実行 px, py = bezie_curve(Q) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(-0.1, 1.1) ax1.set_ylim(-0.1, 1.1) # ベジェ曲線をプロット ax1.plot(px, py, color='red', label='Bezie curve') # 制御点をプロット qx = [] qy = [] for i in range(len(Q)): qx.append(Q[i][0]) qy.append(Q[i][1]) ax1.plot(qx, qy, color='blue', marker='o', linestyle='--', label='Control point') ax1.legend() #ax1.axis('off') # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
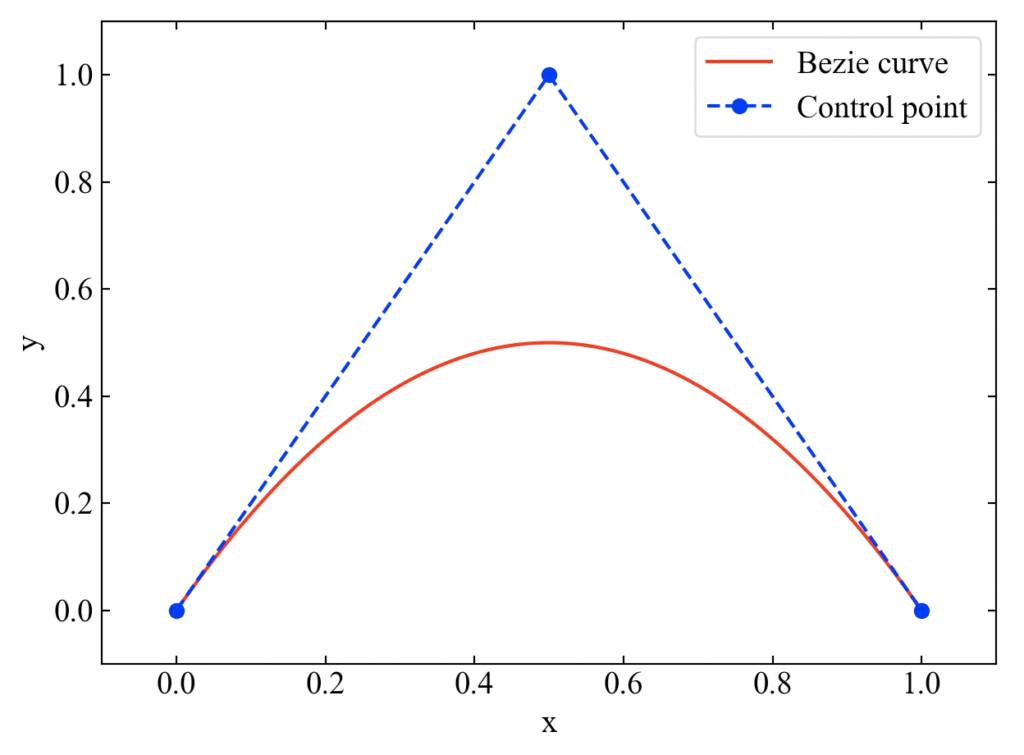
実行すると以下のプロットが表示されます。ベジェ曲線と制御点をプロットしています。
おまけ:【観賞用】ベジェ曲線の動画を作るコード
以下は冒頭で紹介したベジェ曲線のイメージ動画を作成するコードです。create_gif()関数追加、matplotlib内で画像保存…というお粗末なものですが、観賞用にどうぞ。実行するとinputフォルダに静止画が生成され、.py直下にbezie-curve.gifが作成されます。
但し、ブログ記事の素材を作るために書いたものなので、制御点4つまでしか対応していません。制御点5つ以上は一応動画はできますが、直線を増やす所は一般化していないのでご興味のある方は是非Pythonの練習として挑戦してみてください(できたら教えてください)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 |
import numpy as np import math from matplotlib import pyplot as plt import os import glob from PIL import Image # GIFアニメーションを作成 def create_gif(in_dir, out_filename): path_list = sorted(glob.glob(os.path.join(*[in_dir, '*']))) # ファイルパスをソートしてリストする imgs = [] # 画像をappendするための空配列を定義 # ファイルのフルパスからファイル名と拡張子を抽出 for i in range(len(path_list)): img = Image.open(path_list[i]) # 画像ファイルを1つずつ開く imgs.append(img) # 画像をappendで配列に格納していく # appendした画像配列をGIFにする。durationで持続時間、loopでループ数を指定可能。 imgs[0].save(out_filename, save_all=True, append_images=imgs[1:], optimize=False, duration=100, loop=0) # Bernstein多項式を計算する関数 def bernstein(n, t): B = [] for k in range(n + 1): # 二項係数を計算してからBernstein多項式を計算 nCk = math.factorial(n) / (math.factorial(k) * math.factorial(n - k)) B.append(nCk * t ** k * (1 - t) ** (n - k)) print(nCk, k, n-k) return B # ベジェ曲線を描く関数 def bezie_curve(Q): n = len(Q) - 1 dt = 0.01 t = np.arange(0, 1 + dt, dt) B = bernstein(n, t) px = 0 py = 0 for i in range(len(Q)): px += np.dot(B[i], Q[i][0]) py += np.dot(B[i], Q[i][1]) return px, py, t # 点座標を準備 #q1 = [0., 0.] #q2 = [0.5, 1.] #q3 = [1., 0.] #Q = [q1, q2, q3] q1 = [0., 0.] q2 = [0.5, 0.] q3 = [0.5, 1.] q4 = [1., 1.] Q = [q1, q2, q3, q4] # ベジェ曲線を描く関数を実行 px, py, t = bezie_curve(Q) for j in range(len(t)): print(j) # 制御点個数-1(n-1)の線分ができるので、その方程式(傾きと切片)を得る tx = [] ty = [] for i in range(len(Q) - 1): diff_x = Q[i + 1][0] - Q[i][0] if diff_x == 0: diff_y = Q[i + 1][1] - Q[i][1] tx.append(Q[i][0]) ty.append(Q[i][1] + t[j] * diff_y) else: grad = (Q[i + 1][1] - Q[i][1]) / diff_x intercept = Q[i][1] - grad * Q[i][0] tx_temp = Q[i][0] + t[j] * diff_x tx.append(tx_temp) ty.append(grad * tx_temp + intercept) tx2 = [] ty2 = [] for i in range(len(tx) - 1): diff_x2 = tx[i + 1] - tx[i] if diff_x2 == 0: diff_y2 = ty[i + 1] - ty[i] tx2.append(tx[i]) ty2.append(ty[i] + t[j] * diff_y2) else: grad2 = (ty[i + 1] - ty[i]) / diff_x2 intercept2 = ty[i] - grad2 * tx[i] tx_temp2 = tx[i] + t[j] * diff_x2 tx2.append(tx_temp2) ty2.append(grad2 * tx_temp2 + intercept2) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure() ax1 = fig.add_subplot(111) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('x') ax1.set_ylabel('y') # スケールの設定をする。 ax1.set_xlim(-0.1, 1.1) # データプロット ax1.plot(px, py, color='red', label='Bezie curve') qx = [] qy = [] for i in range(len(Q)): qx.append(Q[i][0]) qy.append(Q[i][1]) ax1.plot(qx, qy, color='gray', marker='o', linestyle='--', label='Control point') ax1.plot(tx, ty, color='green', marker='o', linestyle='--', label='sub-line') ax1.plot(tx2, ty2, color='blue', marker='o', linestyle='-', label='sub-line2') ax1.scatter(px[j], py[j], color='blue', label='contact point', s=100) #ax1.legend() #ax1.axis('off') # レイアウト設定 fig.tight_layout() # グラフを表示する。 #plt.show() # dirフォルダが無い時に新規作成 dir = 'input' if os.path.exists(dir): pass else: os.mkdir(dir) # 画像保存パスを準備 path = os.path.join(*[dir, str("{:05}".format(j)) + '.png']) plt.savefig(path) plt.close() # --------------------------------------------------- create_gif(dir, 'bezie-curve.gif') |
こんなのができます。
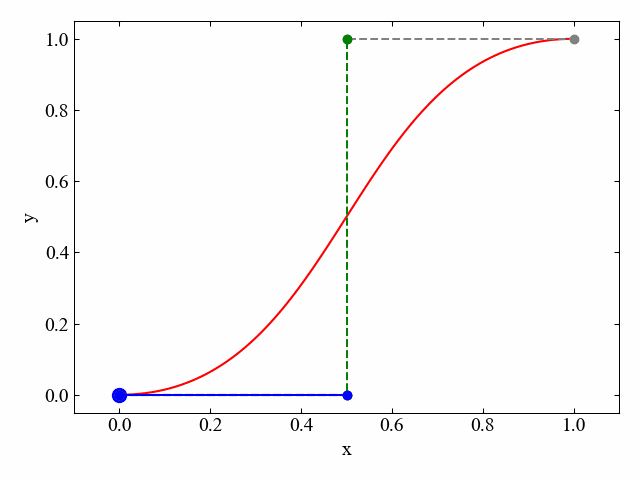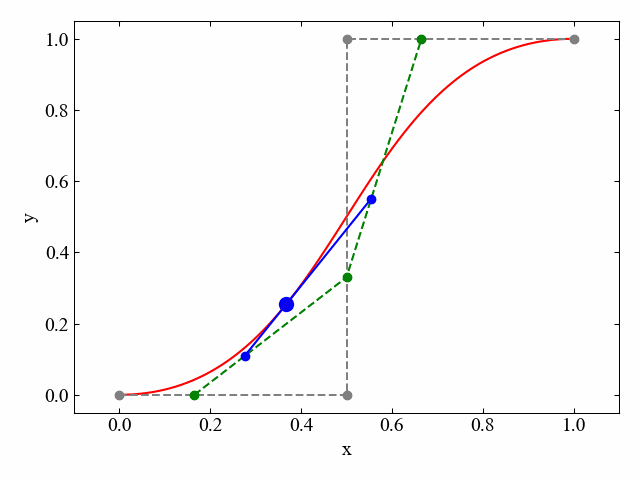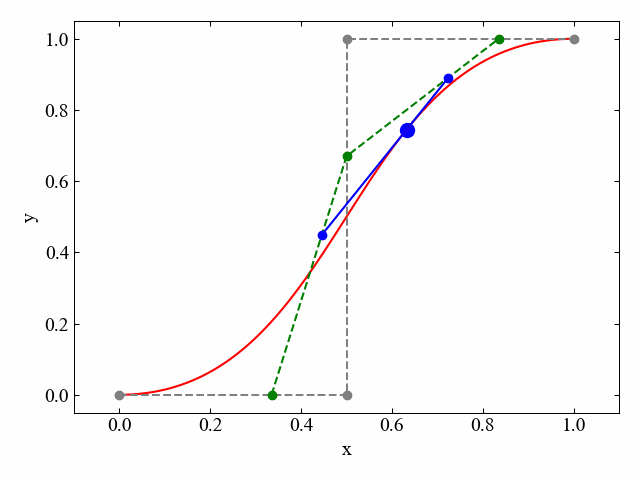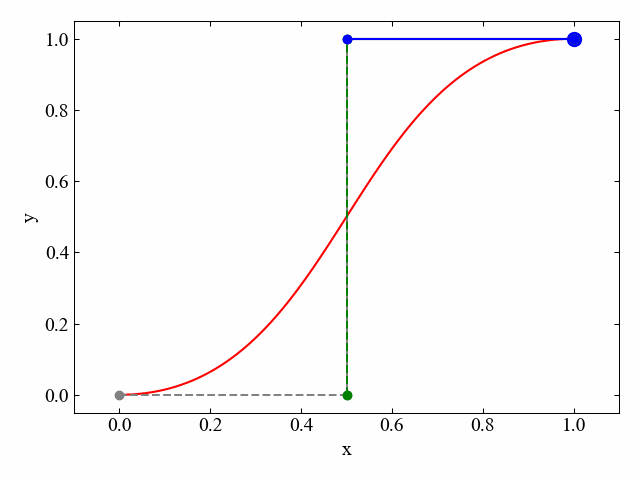
まとめ
この記事ではベジェ曲線がどのような幾何学的原理で描かれるのかに着目して概要を説明しました。
いきなり最終式を紹介しないで解説する事で理解しやすさを高めようとしましたが、もしかしたら冗長でまわりくどい表現になってしまったかも知れません。
コードは自作しましたが、バーンスタイン多項式を一度計算しておいて、最後に制御点毎に内積をとって加算する方式をとりました。これは変数tでforループを回さないよう気を付けただけですが、効率の良い書き方はまだまだあるのではと思います。
今までCADソフトで何気なく使っていたベジェ曲線の描き方がわかってスッキリしました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!