
これまで当ブログではPyVistaを使ってSTLを作ってきましたが、まだ欠落面が存在する3Dモデルでした。ここでは最後の仕上げとして欠落面を閉じた完全な立体を作成、そしてSTLファイルを保存するPythonコードを紹介します。
こんにちは。wat(@watlablog)です。ここではPython/PyVistaで欠落面を閉じたSTLを作成する方法を紹介します!
この記事の目標
PythonでSTLの欠落面を閉じる方法を身につける
当WATLABブログでは過去に「PyVistaをインストールしてPythonでSTLを扱う備忘録」や「Python/PyVistaでSTLモデルを座標変換してみた」という記事でPyVistaを使ってSTLファイルの基本的な扱いを学びました。
PyVistaについては上記記事を参照下さい。
ライブラリを使うとびっくりするくらい簡単にSTLファイルの処理ができるのはすごい!
そして「PyVistaで任意サーフェスメッシュを作成してSTL保存する」で断面プロファイルの押し出しによってサーフェスメッシュを作成、STLファイル保存してみました。
この記事ではサーフェス(面)情報のみのSTLファイルを作成しました。この内容は例えばCAEソフト等で結果を出力する観測面を作成する事には役立ちますが、ソリッドモデル(中身の詰まったモデル)への変換を行ったり、3Dプリンタ用のモデルとして使う事はできません。
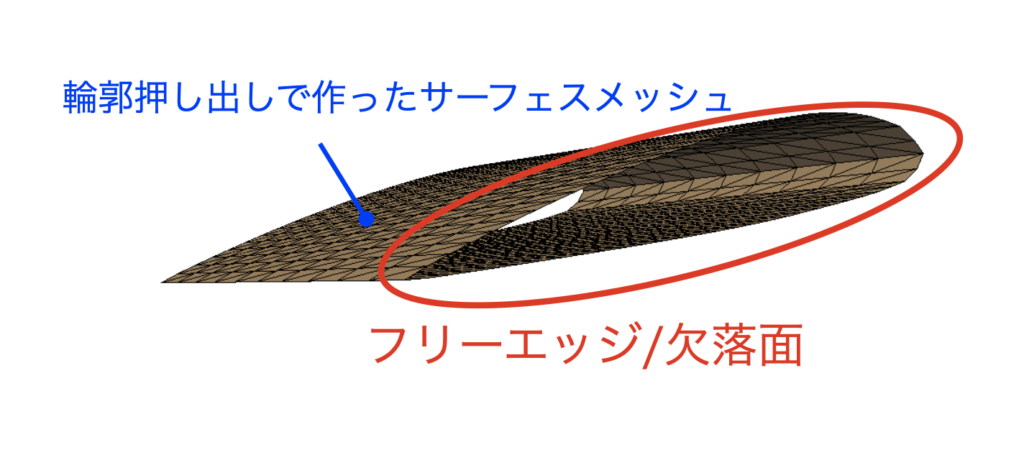
欠落面というのは下図のような開いた面の事で、欠落面を形成している辺をフリーエッジと呼びます。今回は前回のモデルを使ってこの欠落面を埋め、フリーエッジを無くす事を目標とします。
コードの方針
本記事のコードを後半に載せますが、コードを理解するためにもコード上で行っている事を事前に図付きで説明しておきます。
輪郭を押し出してサーフェスを作る
まずはサーフェスを作るための輪郭を作りますが、「def NACA4()」という関数を使います。
ここは「PyVistaで任意サーフェスメッシュを作成してSTL保存する」という記事で詳細を説明していますので、まだ読んでいない方は是非ご覧ください。
この記事では下図の結果を得ます。先ほど紹介した欠落面がある状態です。
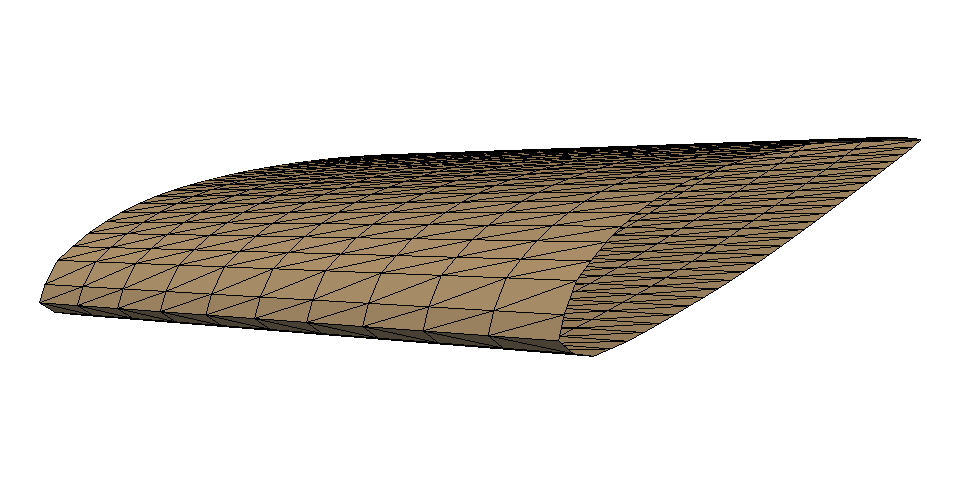
欠落面を埋める事ができるサーフェスを作る
次に、欠落面を埋める事ができるサーフェスを作成します。
目標としては下図の状態を作るワケですが…現状の筆者のスキルだと少しやっかいな方法で工夫するしかありませんでした。

側面の点列データを抽出して座標変換する
工夫の内容を説明します。
この時点で輪郭のサーフェスメッシュが存在します。そして、このメッシュはデローニー三角形分割によりメッシュを作成しています。
PyVistaのデローニー三角形分割は、どうやらxy方向の点列群に対して処理が行われるようでした。
上記理由から輪郭を押し出す方向をy軸に設定していたわけですが、側面に対しては点群を作っただけでは正常に三角形分割されません。
そのため、下図のように面を作りたい点群(ここではy軸の最大値と最小値とセットになっているxyz座標で定義される点群)を抽出した後にy軸とz軸を入れ替える座標変換を実施します。
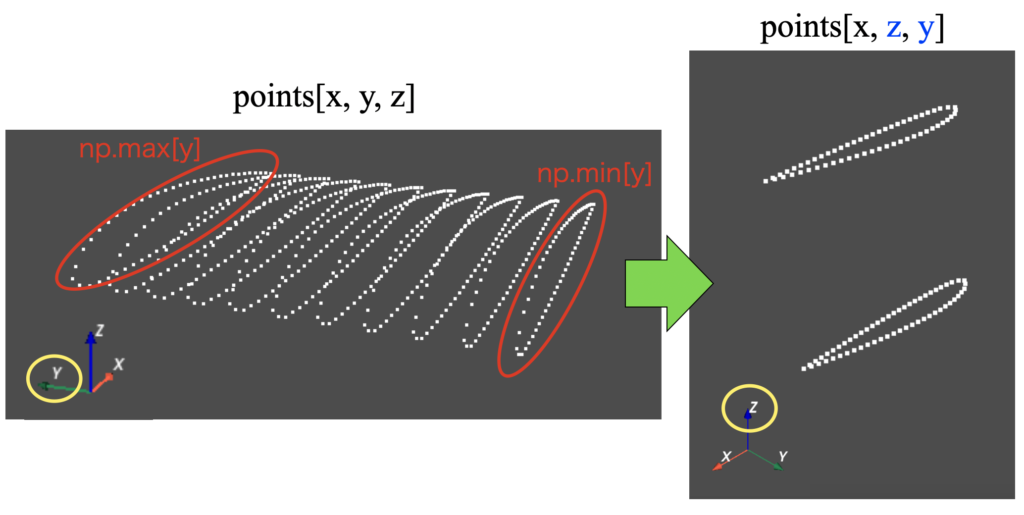
デローニー三角形分割をした後に再び座標変換する
座標変換後であれば、PyVistaのデローニー三角形分割で問題なくサーフェスメッシュを切る事ができます。
2面がくっつかないように1面ずつ切っています。
そしてメッシュを作成した後は、再度y軸とz軸を入れ替えて元の座標系に戻します(下図)。
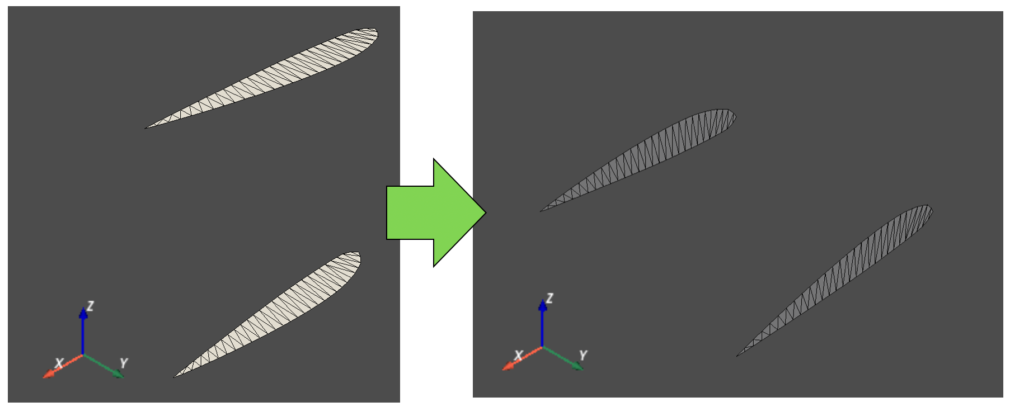
今回はこのような面倒な処理で側面のメッシュを作成しましたが、もしかしてもっと簡単な方法があるのかも知れませんね。PyVistaで何か良い事例があれば是非知りたい所!
デローニー三角形分割は以下のドキュメントを参考にしました。
PyVista:三角形サーフェスを作成
重複節点をマージする
座標変換して元の位置に戻した側面メッシュは、元のメッシュと重ねる事で見かけ上は一体になっているように見えます。
しかし、下図のように異なる面同士が接続される部分は、頂点(ここでは節点と呼んでいます)が重なっています。これを重複節点と呼びます。
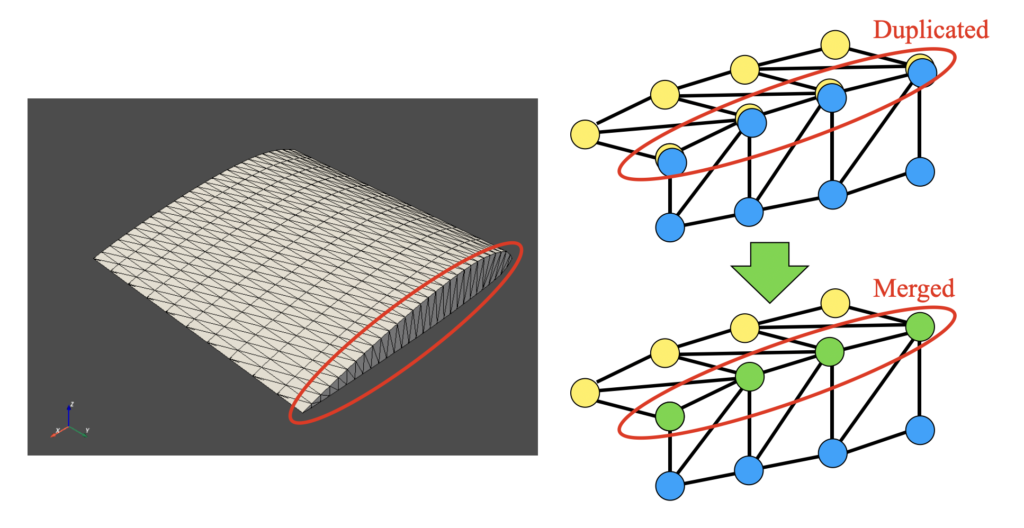
この重複節点はPyVistaであれば「.clean()」にtolerance(公差)を設定してマージする事が可能です。
toleranceを大きくとってしまうと、隣接の節点もマージされてしまい形状が破綻します。そのため面の細かさによってtoleranceの値は調整する必要があります。
本コードでは元のサーフェスメッシュ節点数とマージ後のサーフェスメッシュ節点数がイコールになるかどうかを判定して警告文を出すようにしてみました。
.clean()は以下のドキュメントを参考にしました。
PyVista:pyvista.PolyDataFilters.clean
Python/PyVistaで面が閉じた立体を作ってSTL保存する
全コード
以下に全コードを示します。このコードを実行すると「surf_closed.stl」というSTLファイルが作成されます。
やっている事の概要は上に書きましたが、詳しくはコード内のコメントを参照下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 134 135 136 137 138 139 140 141 142 143 144 145 146 147 148 149 150 151 152 153 154 155 156 157 158 159 160 161 162 163 164 165 166 167 168 169 170 171 172 173 174 175 176 177 |
import numpy as np import pyvista as pv # 最大反り量m, 最大反り位置p, 最大厚み比tからNACA4桁翼形状を作成する関数 def NACA4(m, p, t, x_resolution): # 無次元横軸(0<=x<=1)を作成 x = np.linspace(0, 1, x_resolution) # 公称パラメータを実際の桁に合わせる t = t / 100 m = m / 100 p = p / 10 print('t=', t, 'm=', m, 'p=', p) # 翼厚分布 yt = (t / 0.20) * \ (0.29690 * np.sqrt(x) - 0.12600 * x - 0.35160 * (x ** 2) + 0.28430 * (x ** 3) - 0.10150 * (x ** 4)) # キャンバー線(反り) yc_front = (m / (p ** 2)) * ((2 * p * x) - (x ** 2)) yc_back = (m / (1 - p) ** 2) * ((1 - 2 * p) + (2 * p * x) - (x ** 2)) # 翼厚分布とキャンバー線から翼形状を作成 yc = [] for i in range(len(x)): if x[i] < p: yc.append(yc_front[i]) else: yc.append(yc_back[i]) # 翼厚分布と反りを形状に反映 y_top = yt + yc y_bottom = - yt + yc # 後でサーフェスを閉じるために末尾を0にする y_top[-1] = 0 y_bottom[-1] = 0 # Z座標を設定 z = np.zeros_like(x) # 点列をまとめる points_top = np.column_stack((x, z, y_top)) points_bottom = np.column_stack((x, z, y_bottom)) # 点列データからスプラインを作成 spline_top = pv.Spline(points_top, x_resolution) spline_bottom = pv.Spline(points_bottom, x_resolution) ''' 表示用 cloud1 = pv.PolyData(spline_top.points) cloud2 = pv.PolyData(spline_bottom.points) add = spline_top + spline_bottom + cloud1 + cloud2 add.plot(point_size=15, color='tan') ''' return spline_top, spline_bottom # スプラインから断面一定のNACA翼サーフェスメッシュを作成 def generate_surf_from_spline(spline_top, spline_bottom, length, divisions, round_num): # splineの点データをコピーする(コピーしないと元データが書き換わる) base_top = np.copy(spline_top.points) base_bottom = np.copy(spline_bottom.points) # 押し出し方向の初期値を準備 dy = 0 # divisions数の間隔で点列データを押し出しコピー for i in range(int(divisions)): dy += length / round(divisions, round_num) # y方向の座標に増分値を代入 base_top[:, -2] = np.round(dy, round_num) base_bottom[:, -2] = np.round(dy, round_num) # splineの点列データに行方向に追加 spline_top.points = np.vstack([spline_top.points, base_top]) spline_bottom.points = np.vstack([spline_bottom.points, base_bottom]) # 点列データからXY方向にデローニー三角形分割を行う points_top = pv.PolyData(spline_top.points) points_bottom = pv.PolyData(spline_bottom.points) surf_top = points_top.delaunay_2d() surf_bottom = points_bottom.delaunay_2d() '''表示用 add_points = points_top + points_bottom add_points.plot() ''' # ブーリアン加算演算をして面を一つにする surf_add = surf_top + surf_bottom surf_add = surf_add.clean(tolerance=1e-2) # 面同士が結合している点を重複削除する surf_add.plot(show_edges=True) # 点の数を確認(重複がなくなっていればtop≠bottomとなる) print('top=', len(surf_top.points)) print('bottom=', len(surf_bottom.points)) print('add=', len(surf_add.points)) return surf_add # サーフェスの側面を閉じる関数 def generate_solid_from_surf(surf): # 受け取ったサーフェスメッシュの点列座標を取得 x = surf.points.T[0] y = surf.points.T[1] z = surf.points.T[2] # y軸押し出しで作成したサーフェスのy最大値とy最小値に一致する座標を取得する x_maxy = x[np.where(y == np.max(y))] z_maxy = z[np.where(y == np.max(y))] y_maxy = y[np.where(y == np.max(y))] x_miny = x[np.where(y == np.min(y))] z_miny = z[np.where(y == np.min(y))] y_miny = y[np.where(y == np.min(y))] # y座標とz座標を入れ替える(デーローニー三角形分割を別方向に対して行うため) points_max = np.c_[x_maxy, z_maxy, y_maxy] points_min = np.c_[x_miny, z_miny, y_miny] cloud_max = pv.PolyData(points_max) cloud_min = pv.PolyData(points_min) #(cloud_min + cloud_max).plot(point_size=15) # デーローニー三角形分割を行い側面のサーフェスメッシュを作成する surf_max = cloud_max.delaunay_2d() surf_min = cloud_min.delaunay_2d() #(surf_min + surf_max).plot(show_edges=True) # 座標変換を行うために、側面のメッシュの座標を取得する surf_max_x = surf_max.points.T[0] surf_max_y = surf_max.points.T[1] surf_max_z = surf_max.points.T[2] surf_min_x = surf_min.points.T[0] surf_min_y = surf_min.points.T[1] surf_min_z = surf_min.points.T[2] # z座標とy座標を入れ替える(元の位置に戻すため) surf_max.points = np.c_[surf_max_x, surf_max_z, surf_max_y] surf_min.points = np.c_[surf_min_x, surf_min_z, surf_min_y] (surf_min + surf_max).plot(show_edges=True) # 欠落面を有した元の面と、側面をブーリアン加算する # .cleanで重複節点を探査してマージする surf_closed = (surf + surf_max + surf_min).clean(tolerance=1e-3) # surf==surf_finalになっていれば重複節点は削除されている print('surf=', len(surf.points)) print('surf_max=', len(surf_max.points)) print('surf_min=', len(surf_min.points)) print('surf_final=', len(surf_closed.points)) if len(surf.points) == len(surf_closed.points): print('Successfully completed!') else: print('Some duplicated nodes are remain exist!') print('Change tolerance and retry meshing.') surf_closed.plot(show_edges=True) return surf_closed # NACA4桁翼の断面3D点列座標を計算する関数を実行 resolution = 30 spline_top, spline_bottom = NACA4(m=3, p=3, t=15, x_resolution=resolution) # スプラインから断面一定のNACA翼サーフェスメッシュを作成 surf = generate_surf_from_spline(spline_top, spline_bottom, 1, 10, 1) # サーフェスの側面を閉じる関数 surf_closed = generate_solid_from_surf(surf) # STLファイルを作成 pv.save_meshio('surf_closed.stl', surf_closed) |
他ソフト検証:Blenderでimportしてみた
作成したSTLファイルが他のソフトでも使えるかどうかを確かめるために、3Dモデリングソフトで有名なBlenderでimportしてみました。
結果は正常に読み込まれていました。前回記事の欠落面のある開いたサーフェスメッシュも読み込み可能でしたので、おそらくこのモデルで3Dプリンタ出力とかできるのではないでしょうか?
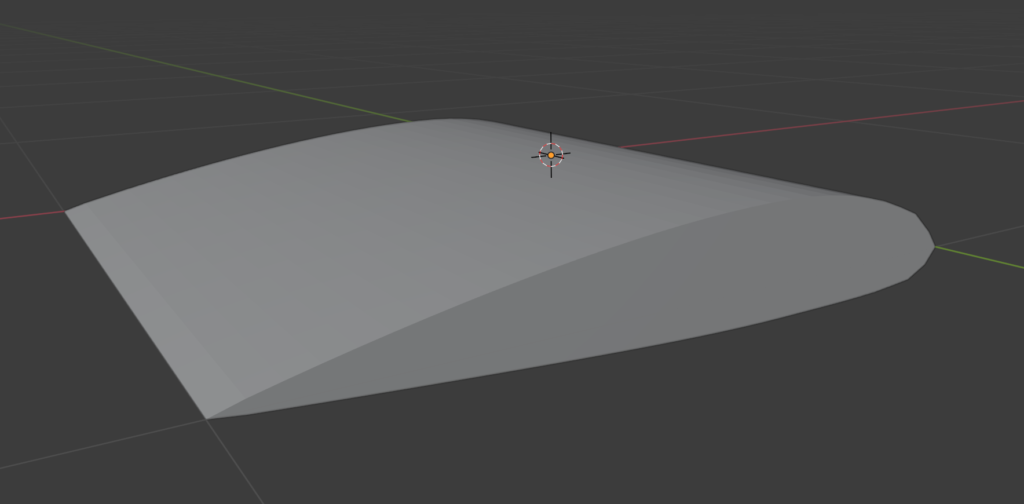
僕は(まだ)3Dプリンタを持っていませんが、数学的に自由な曲面を作成して3Dモデルを作る事ができれば、DIYの幅がグッと広がりそうですね!
おまけ1:モデルの拡大縮小
ここで紹介しているモデルは弦長を1として全て比率で寸法を割り振っています。
実際に3Dプリンタ等で実寸法を扱いたい場合は、元の作図式を実寸法に合わせるよう修正するか、出来上がったモデルの拡大縮小処理をする必要があります。
当ブログの過去記事である「Python/PyVistaでSTLモデルを座標変換してみた」ではSTLファイルの拡大縮小の他に、並進移動や回転移動を紹介しています。是非組み合わせてみて下さい。
おまけ2:背景を白くしてプロット
おまけとして、白背景でSTLファイルを読み込むコードの例を示します。
|
1 2 3 4 5 6 7 8 9 10 |
import pyvista as pv # STlファイルを読み込み mesh = pv.read('surf_closed.stl') # 表示 plotter = pv.Plotter() plotter.set_background('white') actor = plotter.add_mesh(mesh, color='tan', show_edges=True) cpos = plotter.show() |
下図が白背景プロットの例です。当ブログのアイキャッチ画像(タイトル部分の画像)もこれで作っています。
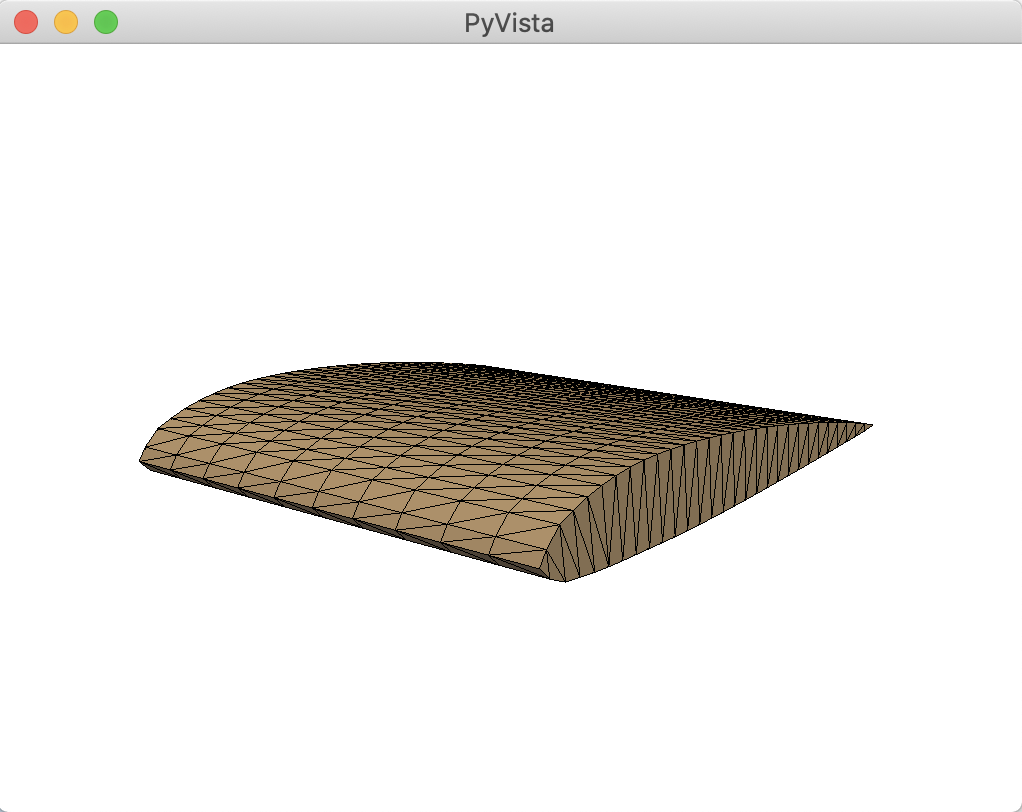
まとめ
本記事ではサーフェスメッシュの開いた面、いわゆるフリーエッジによって形成された欠落面を閉じる方法を紹介しました。
PyVistaのデローニー三角形分割.delauney_2d()と重複節点をマージする.clean()を使うのは過去記事と同じですが、座標変換を繰り返すという事を行いました。
…本当はもっと簡単な方法があるのではないか、と思うようなやり方ですが、今のスキルではこれが精一杯のようです。
(欠落面を自動検出してくれてイイ感じに埋めてくれるメソッドとか無いかな???)
ようやく面を閉じた立体モデルを作る事ができるようになりました!これで色々応用に進めそうです!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!