
周波数応答関数(FRF)はしばしばノイズに悩まされます。正確な評価のためにはノイズを正しく見積もる必要があり、その時はコヒーレンス関数が有用です。ここではPythonでコヒーレンス関数を計算する方法と簡単な分析例を紹介します。
こんにちは。wat(@watlablog)です。ここではFRF分析とセットで使われるコヒーレンス関数の計算方法と計算例を紹介します!
コヒーレンス関数の概要
周波数応答関数のおさらい
本記事ではコヒーレンス関数の使い方を習得し、周波数応答関数のノイズを評価することを目標としますが、まずは周波数応答関数(FRF)について知っておく必要があります。
FRFは以下の式(1)で計算することができます。ここで分母がパワースペクトル、分子がクロススペクトルであることは「Pythonで伝達関数!2つの信号の周波数応答関数を計算する方法」で説明した通りです。
\[
H(\omega )=\frac{O(\omega )I^{\star}(\omega )}{I(\omega )I^{\star}(\omega )} \tag{1}
\]
パワースペクトルを\(P\)、クロススペクトルを\(C\)とし、入力\(i\)と出力\(o\)の関係を添字で表現すると式(2)と書くことも可能です(複素共役で演算することを知っているのが前提ですが、こちらの記法の方がシンプル)。
\[
H(\omega )=\frac{C_{io}(\omega )}{P_{ii}(\omega )} \tag{2}
\]
理想的な条件下であればここまでの知識で2信号の関係を分析することに対して問題はありません。
しかし、リアルワールドデータとしての出力信号には往々にしてノイズが乗ってしまいます。より正確な分析を行うためには、このノイズ成分を評価することが重要です。
ノイズが乗るとどうなる?
式(1)と式(2)の状況は以下の信号系モデルで表現することが可能です。このモデルは任意の伝達系\(h(t)\)に入力\(i(t)\)が入ってきた時に、出力\(o(t)\)を出すという線形モデルです(\(t\)は時間を表します)。
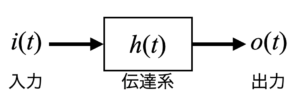
線形で、何のロス(漏れ)もなく、出力に遅延もなく、かつ外乱も入ってこない理想的な状況(理論式ベースのシミュレーション等)では問題無いものの、この状況が1つでも崩れることでそれは出力信号にノイズとなって現れてしまいます。
百聞は一見にしかず…ということで、実際にノイズの有無でFRFがどうなるかを見てみましょう!
理想的なFRFの例
まずは理想的なデータで計算したFRF(ボード線図)の例を以下の図に示します。
入力データはインパルス波形を模擬したForce[N], 出力波形は2自由度ばねマスダンパー系を4次のRunge-Kutta法で解いたシミュレーション結果(Displacement[m])です。
※理想的とは言っても数値解析なので、シミュレーション上の誤差は乗っていますが…。
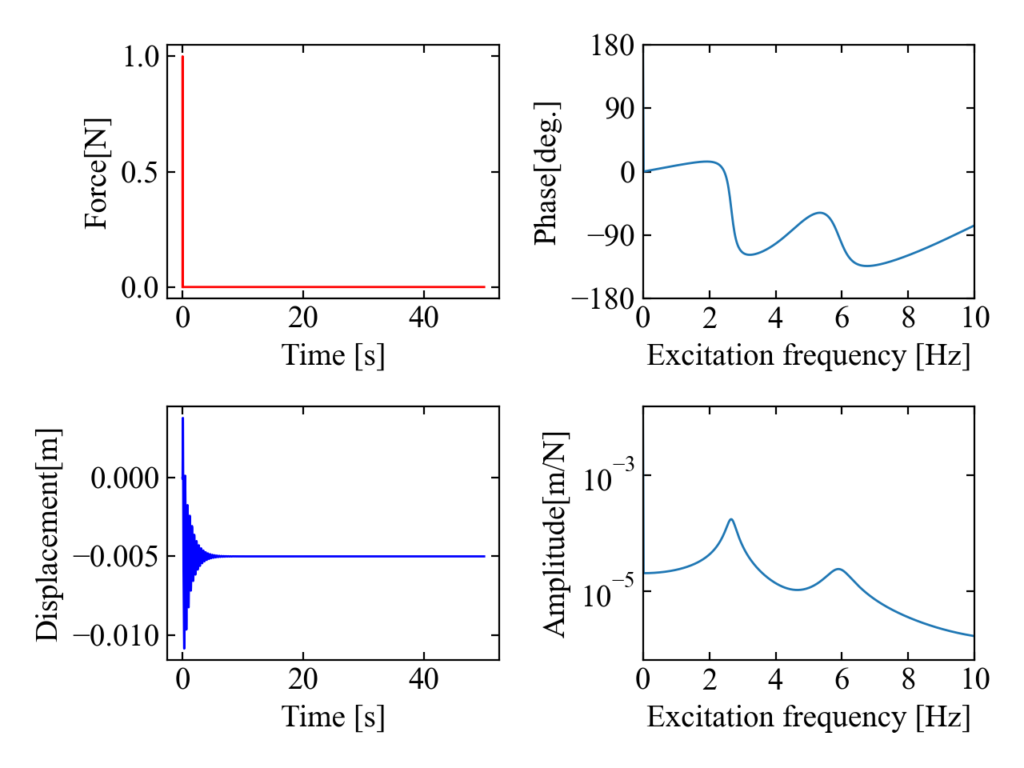
振幅波形(右下)にはピークが2つ、2自由度分綺麗に見えています。これは想定通り。
ノイズが乗ってしまったFRFの例
続いてノイズを重畳させてみましょう。ノイズ成分は出力波形にガウシアンノイズを加算しています。下図がノイズの乗った出力信号で計算したFRFです。
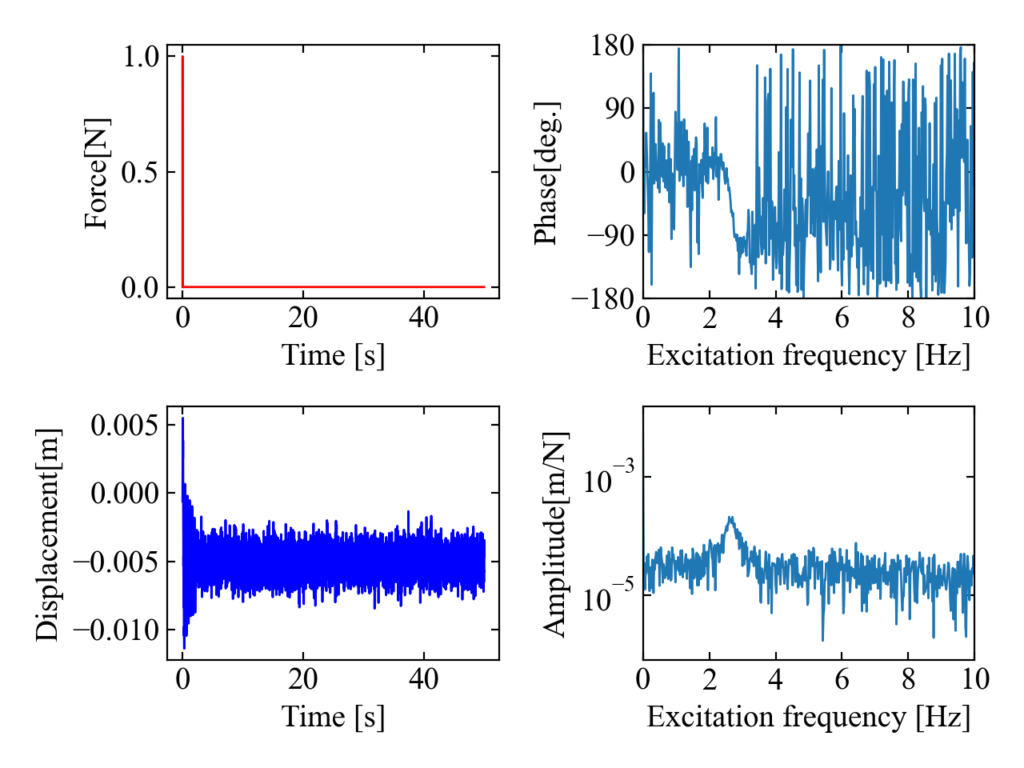
振幅波形には…もはや2つ目のピークは目視で確認できず位相波形(右上)もひどい有様です。
このように、ノイズが乗ってしまうと本来あるはずの情報を正確に分析できないといった大きな問題が生じてしまいます。
ノイズを考慮したモデルとコヒーレンス関数
モデルとノイズ評価の意義
ノイズは様々な状況で信号に加算されます。
実験では測定器の測定範囲に対する計測信号の比が悪いことや、電源ノイズといった外乱、シミュレーションでは時間刻みやアルゴリズム、収束性といった所に原因がある場合が多いでしょうか?
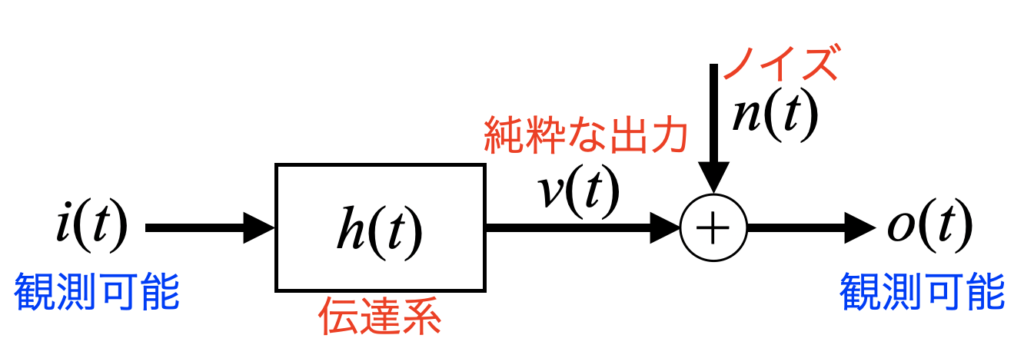
以下の図は出力信号にノイズが重畳する場合の信号系モデルです。先ほどの理想的な系の場合と比べ、伝達系\(h(t)\)から出てきた純粋な出力\(v(t)\)に外乱であるノイズ\(n(t)\)が加算されて最終的な出力\(o(t)\)が得られるという所に違いがあります。
ここで、通常観測可能な物理量としては入力\(i(t)\)と出力\(o(t)\)のみです。周波数応答関数として伝達系を推定しようとしても、ノイズ\(n(t)\)に邪魔をされて純粋な出力\(v(t)\)を抽出することが困難です。
そのため、一般的にはノイズが出来るだけ入らないようにノイズを評価しながら分析していくことが重要とされています。
コヒーレンス関数(関連度関数)の式
それではコヒーレンス関数(Coherence function:※関連度関数とも呼ばれます。)の式を見ていきましょう。
コヒーレンス関数\(\gamma _{io}^{2}(f) \)は式(3)で計算することが出来ます(\(f\)は周波数)。計算はクロススペクトルの絶対値の二乗を入力と出力それぞれのパワースペクトルで除するだけなので、既にFRFを計算したことがあれば簡単ですね。
\[
\gamma _{io}^{2}(f) = \frac{ |C_{io}(f)|^{2}}{P_{ii}(f) P_{oo}(f)}\tag{3}
\]
\[
0 \leq \gamma _{io}^{2}(f) \leq 1
\]
コヒーレンス関数は周波数軸で0から1の間に値をとります。1に近ければコヒーレンス、すなわち入力信号と出力信号の関連度が高いということになります。
式の導出の詳細は「モード解析入門」のP224辺りに載っています。意味合いとしては、周波数領域で定義された相関係数の二乗となるそうです。
コヒーレンス関数は平均化しないと意味がない
式(3)でコヒーレンス関数の計算方法はわかったので、後は実装すれば良いだけですが、1つ注意点があります。
それは、コヒーレンス関数はクロススペクトルとパワースペクトルの平均化をしないと意味がないということです(上記参考書にはP322に記載がありますね)。
この後紹介するPythonコードで計算を実行してみればわかりますが、このコヒーレンス関数は2つの関数がどれくらい似ているのかではなく、再現性があるかどうかを評価する関数です。そのため、複数回ノイズ成分を含んだ計測等を行い、平均化させる必要があります。
Pythonでコヒーレンス関数を計算するコード
サンプルの信号を別.pyファイルで準備する
周波数応答関数の時と同じですが、入力と出力の信号は「simulation.py」を別途作成し、シミュレーションによって用意します。
前回はランダムノイズを加振力として設定していましたが、今回はインパルス波形にしているため再掲します。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 |
import numpy as np # 運動方程式を関数として定義 def f(x, v, f): # 質量・減衰・剛性の集中定数を設定する m1 = 0.1 m2 = 0.05 c1 = 0.6 c2 = 0.3 k1 = 50.0 k2 = 40.0 M = np.array([[m1, 0], # 質量マトリクス [0, m2]]) C = np.array([[c1 + c2, -c2], # 減衰マトリクス [-c2, c2]]) K = np.array([[k1 + k2, -k2], # 剛性マトリクス [-k2, k2]]) M_inv = np.linalg.inv(M) # 質量マトリクスの逆行列 F = np.array([[0.0], [f]]) # 外力ベクトル # 減衰強制振動モデル y = np.dot(M_inv, F) - np.dot((np.dot(C, M_inv)), v) - np.dot((np.dot(K, M_inv)), x) return y # シミュレーションを4次のRunge-Kutta法で実行する関数 def sim(): # 解析条件 t0 = 0.0 # 開始時間 t1 = 50.0 # 終了時間 dt = 1e-2 # 時間刻み # 初期条件 x0 = np.array([[0.0], [0.0]]) # 初期変位[m] v0 = np.array([[0.0], [0.0]]) # 初期速度[m/s] x, v = x0, v0 # 初期値に設定 t_axis = np.arange(t0, t1, dt) # 時間軸 x_sol = [] # 初期化x(変位)配列 v_sol = [] # 初期化v(速度)配列 # インパルスを加振力に設定 force = np.zeros(len(t_axis)) force[1] = 1 # 4次のRunge-Kutta法による数値解析(外力成分を離散1D波形から抽出するバージョン) iteration = 0 for t in t_axis: x_sol.append(x[1, 0]) # 2つ目の自由度の変位を結果として抽出 v_sol.append(v[1, 0]) # 2つ目の自由度の速度を結果として抽出 print('iteration=', iteration,'time=', t, force[iteration]) k11 = f(x, v, force[iteration]) * dt k12 = v * dt k21 = f(x + dt / 2, v + k11 / 2, force[iteration]) * dt k22 = (v + k11 / 2) * dt k31 = f(x + dt / 2, v + k21 / 2, force[iteration]) * dt k32 = (v + k21 / 2) * dt k41 = f(x + dt, v + k31, force[iteration]) * dt k42 = (v + k31) * dt v += (k11 + 2 * k21 + 2 * k31 + k41) / 6 x += (k12 + 2 * k22 + 2 * k32 + k42) / 6 iteration += 1 return force, x_sol, dt, t_axis |
メインコード
import文
続いてメインコードです。import文は定番のnumpy, フーリエ変換用のscipy, グラフ描画用のmatplotlibの他に、先ほど作成したsimulation.pyを読むためのsimulationを記述します。
|
1 2 3 4 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt import simulation |
フーリエ変換する関数
今回は平均化処理を行うため、「Pythonで伝達関数!2つの信号の周波数応答関数を計算する方法」とは異なるコード構成をとっています。以下のようにフーリエ変換をするコードは別途作成しておきます。
この関数はスペクトルを得るためのinput, outputの時間波形と周波数軸を計算するための時間刻みdtを入力して使います。
|
1 2 3 4 5 6 |
# 入力信号と出力信号のフーリエ変換をする関数 def fft(input, output, dt): fft_i = fftpack.fft(input) # 入力信号のフーリエ変換 fft_o = fftpack.fft(output) # 出力信号のフーリエ変換 freq = np.linspace(0, 1 / dt, len(input)) # 周波数軸を作成 return fft_i, fft_o, freq |
FRFとコヒーレンス関数を計算する関数
周波数応答関数(FRF)とコヒーレンス関数は同じ関数の中で計算します。
その理由は、平均化を考慮しているからです。
この関数は複数回分のクロススペクトルとパワースペクトルを関数の外でも中でも保持できるように、入力と出力の両方に「〜_list」という変数を設定しています(シフトレジスタ的にしたかった)。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 |
# 周波数応答関数(FRF)とコヒーレンス関数を計算する関数(平均化機能付き) def frf_mean(fft_i, fft_o, c_io_list, p_ii_list, p_oo_list): c_io = fft_o * fft_i.conjugate() # inputとoutputのクロススペクトルを計算 p_ii = fft_i * fft_i.conjugate() # inputのパワースペクトルを計算 p_oo = fft_o * fft_o.conjugate() # outputのパワースペクトルを計算 # 平均化のためにリストに追加 c_io_list.append(c_io) p_ii_list.append(p_ii) p_oo_list.append(p_oo) # axis=0でリストの列方向に平均化(周波数軸で平均化)する c_io_mean = np.mean(c_io_list, axis=0) p_ii_mean = np.mean(p_ii_list, axis=0) p_oo_mean = np.mean(p_oo_list, axis=0) # 周波数応答関数(FRF)を計算する h_io = c_io_mean / p_ii_mean # コヒーレンス関数を計算する coherence = (abs(c_io_mean) ** 2) / (p_ii_mean * p_oo_mean) return h_io, coherence, c_io_list, p_ii_list, p_oo_list |
ボード線図描画のための関数
ボード線図のための振幅と位相の計算は関数で用意しておいた方が、今回の平均化FRFの場合は便利だったので、以下のコードのように準備しておきます。
|
1 2 3 4 5 6 7 |
# FRFからボード線図を計算する関数 def bode_plot(h_io): amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) # FRFの振幅成分 amp = amp / (len(input) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(h_io.imag, h_io.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 return amp, phase |
各種関数の実行とグラフ描画
最後は各種関数を実行するための文とグラフ描画のための文を書いておしまいです。forループを使ってシミュレーションを3回計算し、毎回新しいノイズを重畳してFRFを計算していくという内容です。
もしこのプログラムを測定用に使う場合は、simulation()の部分をデータ収集コードに換えることで実現できると思います。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 |
# 平均化のために空リストを作成 c_io_list = [] p_ii_list = [] p_oo_list = [] # 平均化回数分のループを設定 for i in range(3): # サンプル信号を準備する(別ファイルで作成したsimulation.pyのsim()関数で計算) input, output, dt, t_axis = simulation.sim() # 出力信号にガウシアンノイズを重畳する output += 2e-4 * np.random.normal(loc=0, scale=1, size=len(t_axis)) # 入力信号と出力信号のフーリエ変換 fft_i, fft_o, freq = fft(input, output, dt) # 平均化FRFとコヒーレンス関数を計算する h_io, coherence, c_io_list, p_ii_list, p_oo_list = frf_mean(fft_i, fft_o, c_io_list, p_ii_list, p_oo_list) # 平均化FRFからボード線図用の振幅と位相を計算する amp, phase = bode_plot(h_io) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(12,4)) ax1 = fig.add_subplot(231) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(234) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(232) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(235) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') ax5 = fig.add_subplot(133) ax5.yaxis.set_ticks_position('both') ax5.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') ax5.set_xlabel('Excitation frequency [Hz]') ax5.set_ylabel('Coherence') # スケールの設定をする。 ax3.set_xticks(np.arange(0, 20, 2)) ax3.set_xlim(0, 10) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax4.set_xticks(np.arange(0, 20, 2)) ax4.set_xlim(0, 10) ax4.set_yscale('log') ax5.set_xticks(np.arange(0, 20, 2)) ax5.set_xlim(0, 10) ax5.set_yticks(np.arange(0, 2, 0.2)) ax5.set_ylim(0, 1.05) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='Input', lw=1, color='red') ax2.plot(t_axis, output, label='Output', lw=1, color='blue') ax3.plot(freq, phase, lw=1) ax4.plot(freq, amp, lw=1) ax5.plot(freq, coherence, lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
実行結果
このコードを実行することで、以下の図のような結果を得ます。左から時間波形、FRF(ボード線図)、コヒーレンス関数です。
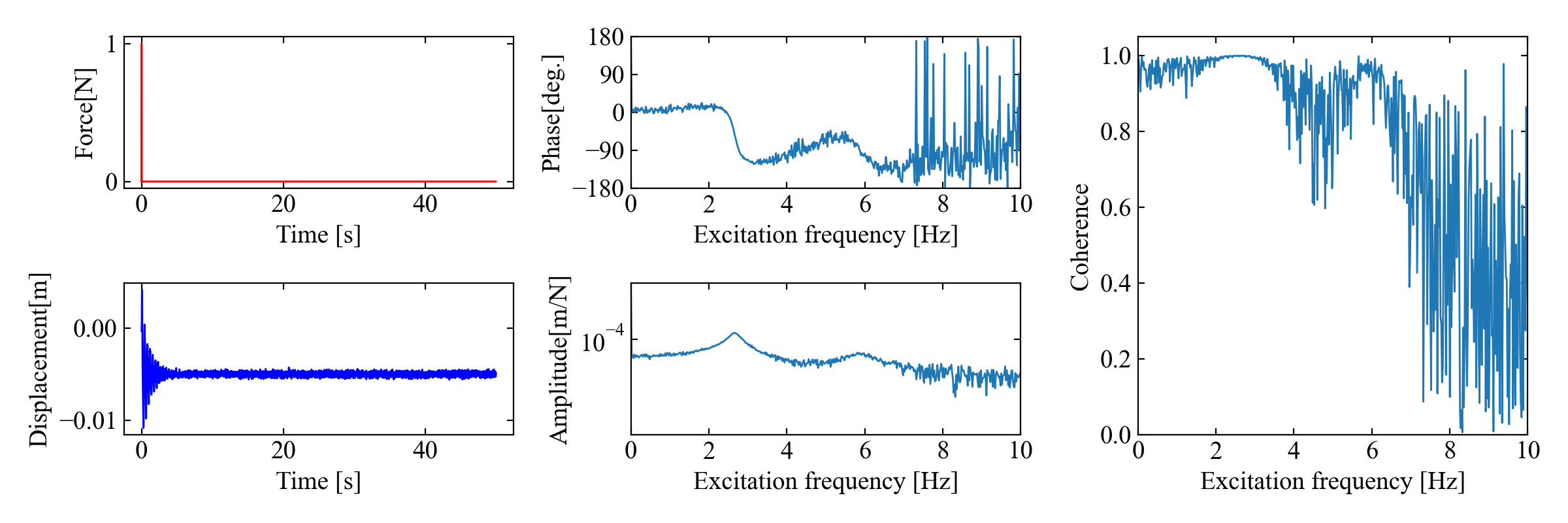
ノイズ違いで比較してみる
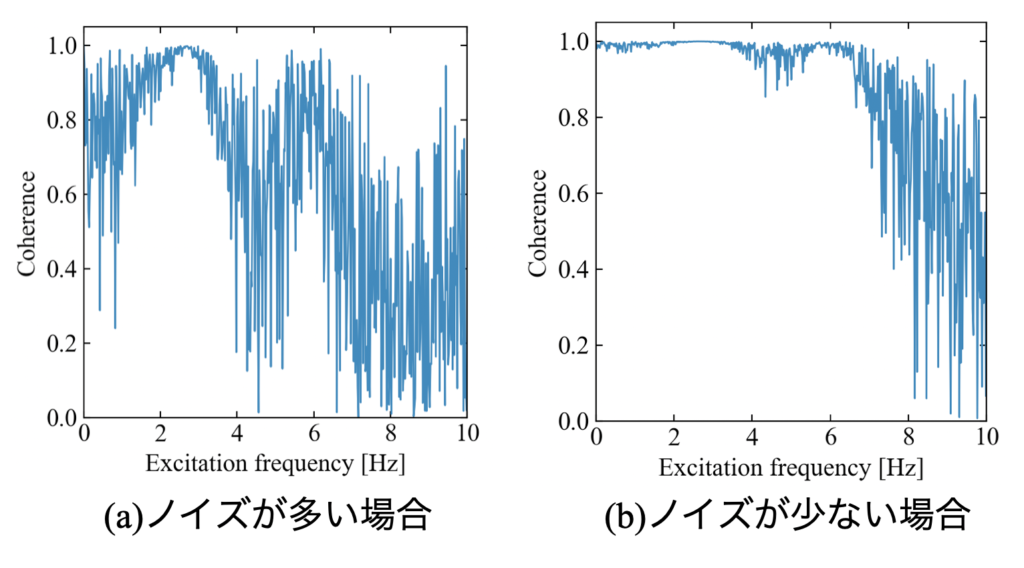
ガウシアンノイズの振幅を調整し、ノイズの量でコヒーレンス関数の値がどう変わるのかを下図で比較してみました。
今回は2自由度の振動シミュレーションを信号として使っているので、FRFには振動モードが存在することが特徴です。
(a)ノイズが多い場合は(b)ノイズが少ない場合に比べて全体的にコヒーレンス値が低い傾向にありますが、モード部分は比較的高い値を維持しようとしている特徴がありました。
実験であれば測定毎に毎回コヒーレンスを評価し、著しく値が低下しないかどうかを確認することが良いとされています。
(モード周波数の部分がよければ後はOKと妥協することもありますが…。)
メインコード全文(コピペ用)
コピペしやすいようにメインコード部分全コードを以下に示します。
是非信号や平均化回数と条件を変えて遊んでみて下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 85 86 87 88 89 90 91 92 93 94 95 96 97 98 99 100 101 102 103 104 105 106 107 108 109 110 111 112 113 114 115 116 117 118 119 120 121 122 123 124 125 126 127 128 129 130 131 132 133 |
import numpy as np from scipy import fftpack import matplotlib.pyplot as plt import simulation # 入力信号と出力信号のフーリエ変換をする関数 def fft(input, output, dt): fft_i = fftpack.fft(input) # 入力信号のフーリエ変換 fft_o = fftpack.fft(output) # 出力信号のフーリエ変換 freq = np.linspace(0, 1 / dt, len(input)) # 周波数軸を作成 return fft_i, fft_o, freq # 周波数応答関数(FRF)とコヒーレンス関数を計算する関数(平均化機能付き) def frf_mean(fft_i, fft_o, c_io_list, p_ii_list, p_oo_list): c_io = fft_o * fft_i.conjugate() # inputとoutputのクロススペクトルを計算 p_ii = fft_i * fft_i.conjugate() # inputのパワースペクトルを計算 p_oo = fft_o * fft_o.conjugate() # outputのパワースペクトルを計算 # 平均化のためにリストに追加 c_io_list.append(c_io) p_ii_list.append(p_ii) p_oo_list.append(p_oo) # axis=0でリストの列方向に平均化(周波数軸で平均化)する c_io_mean = np.mean(c_io_list, axis=0) p_ii_mean = np.mean(p_ii_list, axis=0) p_oo_mean = np.mean(p_oo_list, axis=0) # 周波数応答関数(FRF)を計算する h_io = c_io_mean / p_ii_mean # コヒーレンス関数を計算する coherence = (abs(c_io_mean) ** 2) / (p_ii_mean * p_oo_mean) return h_io, coherence, c_io_list, p_ii_list, p_oo_list # FRFからボード線図を計算する関数 def bode_plot(h_io): amp = np.sqrt((h_io.real ** 2) + (h_io.imag ** 2)) # FRFの振幅成分 amp = amp / (len(input) / 2) # 振幅成分の正規化(辻褄合わせ) phase = np.arctan2(h_io.imag, h_io.real) # 位相を計算 phase = np.degrees(phase) # 位相をラジアンから度に変換 return amp, phase # 平均化のために空リストを作成 c_io_list = [] p_ii_list = [] p_oo_list = [] # 平均化回数分のループを設定 for i in range(3): # サンプル信号を準備する(別ファイルで作成したsimulation.pyのsim()関数で計算) input, output, dt, t_axis = simulation.sim() # 出力信号にガウシアンノイズを重畳する output += 1e-4 * np.random.normal(loc=0, scale=1, size=len(t_axis)) # 入力信号と出力信号のフーリエ変換 fft_i, fft_o, freq = fft(input, output, dt) # 平均化FRFとコヒーレンス関数を計算する h_io, coherence, c_io_list, p_ii_list, p_oo_list = frf_mean(fft_i, fft_o, c_io_list, p_ii_list, p_oo_list) # 平均化FRFからボード線図用の振幅と位相を計算する amp, phase = bode_plot(h_io) # ここからグラフ描画------------------------------------- # フォントの種類とサイズを設定する。 plt.rcParams['font.size'] = 14 plt.rcParams['font.family'] = 'Times New Roman' # 目盛を内側にする。 plt.rcParams['xtick.direction'] = 'in' plt.rcParams['ytick.direction'] = 'in' # グラフの上下左右に目盛線を付ける。 fig = plt.figure(figsize=(12,4)) ax1 = fig.add_subplot(231) ax1.yaxis.set_ticks_position('both') ax1.xaxis.set_ticks_position('both') ax2 = fig.add_subplot(234) ax2.yaxis.set_ticks_position('both') ax2.xaxis.set_ticks_position('both') ax3 = fig.add_subplot(232) ax3.yaxis.set_ticks_position('both') ax3.xaxis.set_ticks_position('both') ax4 = fig.add_subplot(235) ax4.yaxis.set_ticks_position('both') ax4.xaxis.set_ticks_position('both') ax5 = fig.add_subplot(133) ax5.yaxis.set_ticks_position('both') ax5.xaxis.set_ticks_position('both') # 軸のラベルを設定する。 ax1.set_xlabel('Time [s]') ax1.set_ylabel('Force[N]') ax2.set_xlabel('Time [s]') ax2.set_ylabel('Displacement[m]') ax3.set_xlabel('Excitation frequency [Hz]') ax3.set_ylabel('Phase[deg.]') ax4.set_xlabel('Excitation frequency [Hz]') ax4.set_ylabel('Amplitude[m/N]') ax5.set_xlabel('Excitation frequency [Hz]') ax5.set_ylabel('Coherence') # スケールの設定をする。 ax3.set_xticks(np.arange(0, 20, 2)) ax3.set_xlim(0, 10) ax3.set_yticks(np.arange(-270, 270, 90)) ax3.set_ylim(-180, 180) ax4.set_xticks(np.arange(0, 20, 2)) ax4.set_xlim(0, 10) ax4.set_yscale('log') ax5.set_xticks(np.arange(0, 20, 2)) ax5.set_xlim(0, 10) ax5.set_yticks(np.arange(0, 2, 0.2)) ax5.set_ylim(0, 1.05) # データプロットの準備とともに、ラベルと線の太さ、凡例の設置を行う。 ax1.plot(t_axis, input, label='Input', lw=1, color='red') ax2.plot(t_axis, output, label='Output', lw=1, color='blue') ax3.plot(freq, phase, lw=1) ax4.plot(freq, amp, lw=1) ax5.plot(freq, coherence, lw=1) # レイアウト設定 fig.tight_layout() # グラフを表示する。 plt.show() plt.close() # --------------------------------------------------- |
まとめ
本記事では周波数応答関数(FRF)の評価に必要不可欠なコヒーレンス関数の概要を説明し、Pythonによる実装方法を紹介しました。
コヒーレンス関数は平均化処理が必須であり、信号同士の再現性を分析、ノイズ成分の大小を評価することができます。
ノイズ評価は様々な工学的場面で重要となりますので、是非活用してみて下さい。
FRFとともにコヒーレンス関数のPythonコードを習得しました!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
