
複素力学系で有名な図にマンデルブロ集合がありますが、同じ漸化式を異なる条件で計算するとジュリア集合を計算する事が出来ます。ここでは、Pythonによるジュリア集合を描画し、さらに変数を連続的に変化させた場合で動画にする方法を紹介します。
こんにちは。wat(@watlablog)です。マンデルブロ集合の次はジュリア集合を描画してみます!
ジュリア集合とマンデルブロ集合の関係
漸化式はマンデルブロ集合と同じ
ジュリア集合の説明をする前に、まずはマンデルブロ集合をおさらいしてみましょう。
マンデルブロ集合とは、以下の漸化式を初期値\(z_{0}=0\)、複素数\(c\)に複素平面上の座標を代入した条件下で反復計算を行って収束するか発散するかを調べ、結果をプロットして出来る図です。
\[
z_{n+1}=z_{n}^{2}+c
\]
マンデルブロ集合を描画すると、以下のように非常に不思議な図を得ることが出来ます。
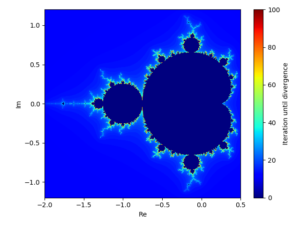
マンデルブロ集合は拡大して見ていくとフラクタル図形の世界を旅することが出来ます。詳しくは「Pythonで描くマンデルブロ集合!フラクタルの旅を体感してみる」の記事をご覧下さい。
ジュリア集合の条件
一方、ジュリア集合もマンデルブロ集合と同じ上記の漸化式を使います。先ほどは\(z_{0}=0\)として\(c\)を変動させていましたが、ジュリア集合をプロットするためにはその逆に\(c\)を固定して\(z_{0}\)に複素平面上の座標を代入させます。
詳細は本ページの後半に載せるプログラムコードを参照下さい。
ちなみにジュリア集合を計算すると、以下のような図を得ることが出来ます。

それでは早速プログラムを書いてみましょう。
Pythonでジュリア集合を描画するコード
固定変数で単一のジュリア集合を描く
まずは基本の描画として、複素数の実部(コードではa)と虚部(コードではb)を1つだけ設定してジュリア集合を描画するプログラムを以下に示します。
プログラムはほぼマンデルブロ集合の時と同じなので、詳しい説明は先の記事のコード部分をご確認下さい。
また、このプログラムはnumbaをimportしてJIT(Just In Time compile)を使って高速化しています。高速化を行うと僕の環境では約1[s]ほどで計算が終了しますが、JITを使わないと数十倍の計算時間になってしまいます。
numbaについては「NumbaのJITでPythonを高速化したら40倍も速くなった」に詳細を書きましたのでご確認下さい。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 |
import numpy as np from matplotlib import pyplot as plt from matplotlib.colors import Normalize # カラーマップを自在に操作するために必要 from numba import jit # これが無いとおそろしく計算時間がかかる import time # 計算時間を見るために必要 t0 = time.time() @jit # NumbaによるJust In Time Compileを実行 def julia(z_real, z_imag, n_max, a, b): Re, Im = np.meshgrid(z_real, z_imag) # ReとImの組み合わせを計算 n_grid = len(Re.ravel()) # 組み合わせの総数 z = np.zeros(n_grid) # ジュリア集合のデータ格納用空配列 # zにジュリア集合に属するか否かのデータを格納していくループ for i in range(n_grid): c = complex(a, b) # 複素数cを定義 # イタレーション回数nと複素数z0を初期化 n = 0 z0 = complex(Re.ravel()[i], Im.ravel()[i]) # z0が無限大になるか、最大イタレーション数になるまでループする while np.abs(z0) < 1e20 and not n == n_max: z0 = z0 ** 2 + c # 漸化式を計算 n += 1 # イタレーション数を増分 # z0が無限大に発散する場合はn, 収束する場合は0を格納 if n == n_max: z[i] = 0 else: z[i] = n # 計算の進捗度をモニター(毎ループだと計算が遅くなるため) if i % 100000 == 0: print(i, '/',n_grid, (i/n_grid)*100) z = np.reshape(z, Re.shape) # 2次元配列(画像表示用)にリシェイプ z = z[::-1] # imshow()で上下逆になるので予め上下反転 return z # 水平方向h(実部Re)と垂直方向v(虚部Im)の範囲を決める h1 = -1.5 h2 = 1.5 v1 = -1.5 v2 = 1.5 # 分解能を設定 resolution = 1000 # 実部と虚部の軸データ配列、最大イタレーション数を設定 z_real = np.linspace(h1, h2, resolution) z_imag = np.linspace(v1, v2, resolution) n_max = 100 a = -0.8 b = 0.15 # 関数を実行し画像を得る z = julia(z_real, z_imag, n_max, a, b) t1 = time.time() print('Calculation time=', float(t1 - t0), '[s]') # ここからグラフ表示---------------------------------------- fig = plt.figure() ax1 = fig.add_subplot(111) ax1.set_xlabel('Re') ax1.set_ylabel('Im') ax1.text(-1.4, 1.3, 'a=' + str(a), size=10, color='yellow') ax1.text(-1.4, 1.2, 'b=' + str(b), size=10, color='yellow') mappable = ax1.imshow(z, cmap='seismic', norm=Normalize(vmin=0, vmax=n_max), extent=[h1, h2, v1, v2]) cbar = plt.colorbar(mappable=mappable, ax=ax1) cbar.set_label('Iteration until divergence') cbar.mappable.set_clim(0, n_max) ax1.axis('off') plt.tight_layout() plt.show() plt.close() # ---------------------------------------------------------- |
上記コードを実行すると以下の図を得ます。これがジュリア集合です。
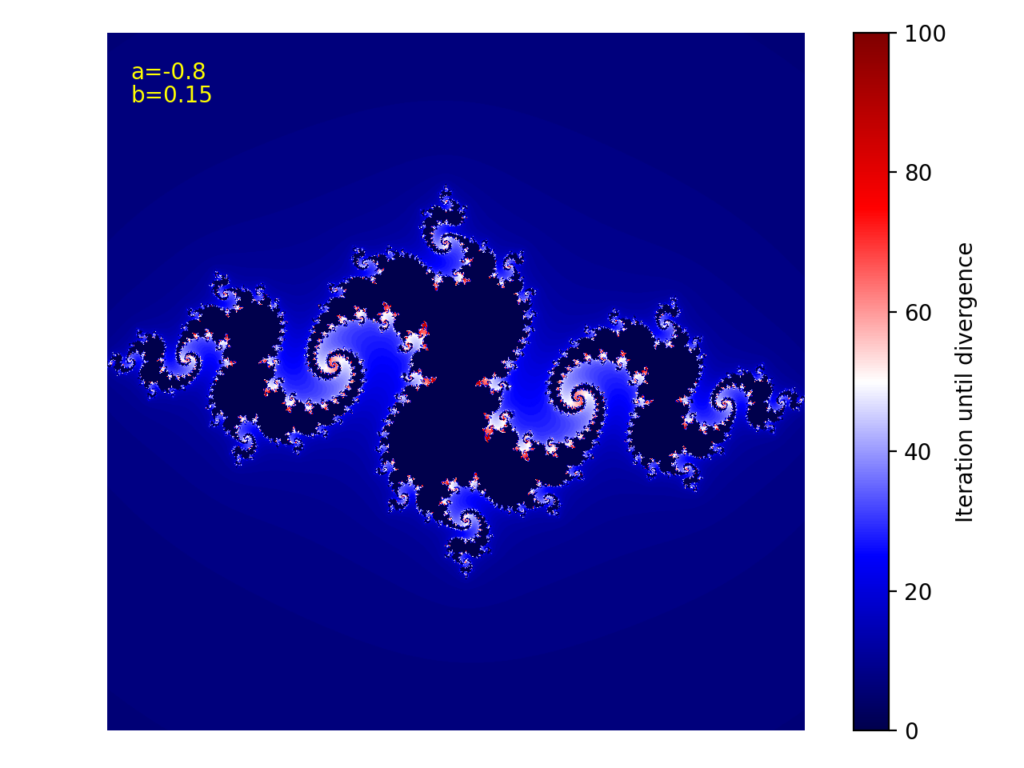
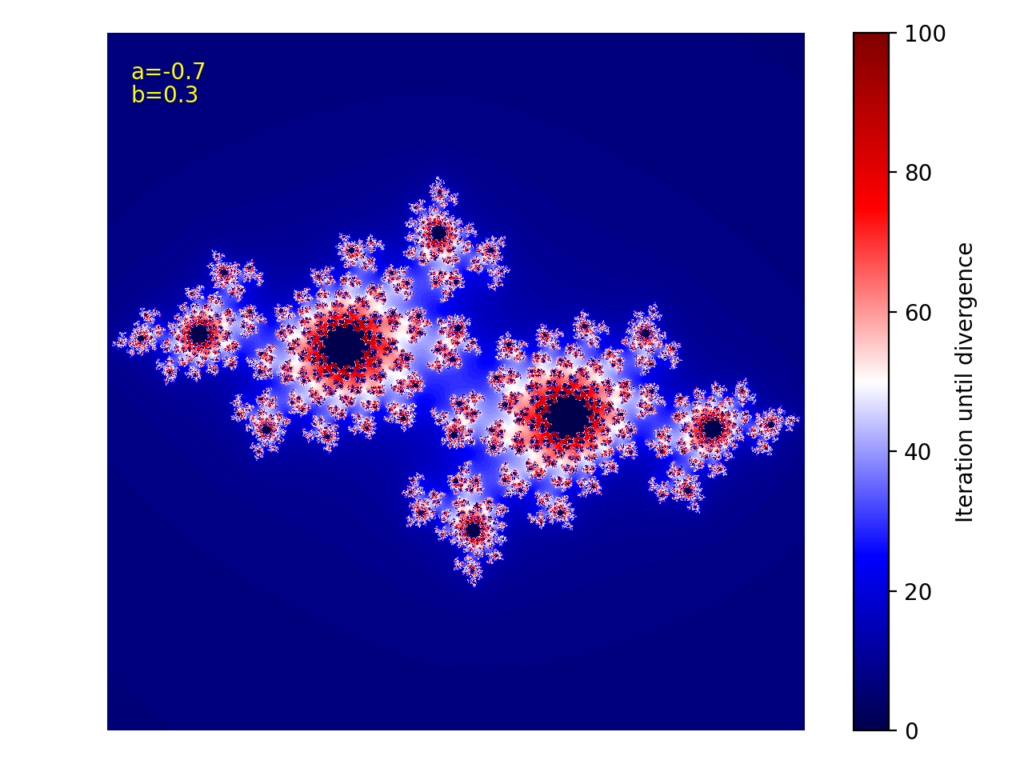
cの実部と虚部を少し変更すると、また違った図を得ますので、是非色々試してみて下さい!
変動変数で動画用の連続画像を作成する
ジュリア集合はcの値を変化させることで様々な模様の変化をします。
このことから「実部と虚部の値を連続的に少しずつ変化させたらどうなるのか?」という興味が湧いてきたので、プログラムで表現してみます。
以下のコードはジュリア集合計算部分をforループで囲み、変数を少しずつ変化させながらプロットを画像として保存していくプログラムです。
(動画化はフリーソフトを使ってやった方が簡単だったのでPythonでは実装していません)
これだけの計算量をこなせるのは、numbaのおかげ。
|
1 2 3 4 5 6 7 8 9 10 11 12 13 14 15 16 17 18 19 20 21 22 23 24 25 26 27 28 29 30 31 32 33 34 35 36 37 38 39 40 41 42 43 44 45 46 47 48 49 50 51 52 53 54 55 56 57 58 59 60 61 62 63 64 65 66 67 68 69 70 71 72 73 74 75 76 77 78 79 80 81 82 83 84 |
import numpy as np from matplotlib import pyplot as plt from matplotlib.colors import Normalize # カラーマップを自在に操作するために必要 from numba import jit # これが無いとおそろしく計算時間がかかる import time # 計算時間を見るために必要 t0 = time.time() @jit # NumbaによるJust In Time Compileを実行 def julia(z_real, z_imag, n_max, a, b): Re, Im = np.meshgrid(z_real, z_imag) # ReとImの組み合わせを計算 n_grid = len(Re.ravel()) # 組み合わせの総数 z = np.zeros(n_grid) # ジュリア集合のデータ格納用空配列 # zにジュリア集合に属するか否かのデータを格納していくループ for i in range(n_grid): c = complex(a, b) # 複素数cを定義 # イタレーション回数nと複素数z0を初期化 n = 0 z0 = complex(Re.ravel()[i], Im.ravel()[i]) # z0が無限大になるか、最大イタレーション数になるまでループする while np.abs(z0) < 1e20 and not n == n_max: z0 = z0 ** 2 + c # 漸化式を計算 n += 1 # イタレーション数を増分 # z0が無限大に発散する場合はn, 収束する場合は0を格納 if n == n_max: z[i] = 0 else: z[i] = n # 計算の進捗度をモニター(毎ループだと計算が遅くなるため) if i % 100000 == 0: print(i, '/',n_grid, (i/n_grid)*100) z = np.reshape(z, Re.shape) # 2次元配列(画像表示用)にリシェイプ z = z[::-1] # imshow()で上下逆になるので予め上下反転 return z # 水平方向h(実部Re)と垂直方向v(虚部Im)の範囲を決める h1 = -1.5 h2 = 1.5 v1 = -1.5 v2 = 1.5 # 分解能を設定 resolution = 1000 # 実部と虚部の軸データ配列、最大イタレーション数を設定 z_real = np.linspace(h1, h2, resolution) z_imag = np.linspace(v1, v2, resolution) n_max = 100 a = np.linspace(-0.9, -0.3, 50) b = np.linspace(0, 0.7, 50) for k in range(len(a)): # 関数を実行し画像を得る z = julia(z_real, z_imag, n_max, a[k], b[k]) print(str(k) + '/' + str(len(a))) # ここからグラフ表示---------------------------------------- fig = plt.figure() ax1 = fig.add_subplot(111) ax1.set_xlabel('Re') ax1.set_ylabel('Im') ax1.text(-1.4, 1.3, 'a=' + str(a[k]), size=10, color='yellow') ax1.text(-1.4, 1.2, 'b=' + str(b[k]), size=10, color='yellow') mappable = ax1.imshow(z, cmap='seismic', norm=Normalize(vmin=0, vmax=n_max), extent=[h1, h2, v1, v2]) cbar = plt.colorbar(mappable=mappable, ax=ax1) cbar.set_label('Iteration until divergence') cbar.mappable.set_clim(0, n_max) ax1.axis('off') plt.tight_layout() #plt.show() plt.savefig('fig_' + str("{:05}".format(k)) + '.png') plt.close() # ---------------------------------------------------------- t1 = time.time() print('Calculation time=', float(t1 - t0), '[s]') |
上記コードを実行すると50枚ほどの画像が生成されます。その画像をフリーソフトでまとめたものが以下のGIF動画です。
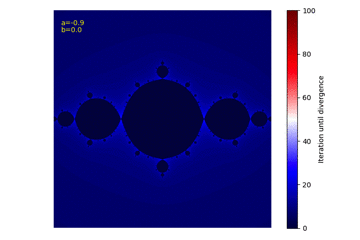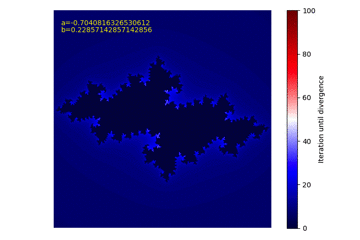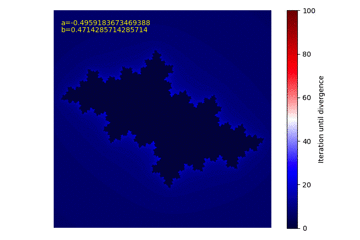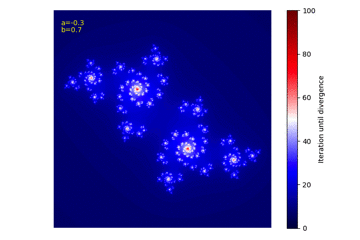
全体的に時計回りに回転しながら、まるで花が咲いて散り、また咲くような面白い動きを観測することが出来ました!
まとめ
本記事ではマンデルブロ集合の親戚であるジュリア集合を紹介し、Pythonプログラムで描画する方法を紹介しました。
また、ジュリア集合は条件によって模様を変える特徴を持つため、プログラム内で連続的に値を変化させた時の挙動を観測することを行ってみました。
結果、その模様変化は連続的で大変美しいものと確認出来ました。
変数の取り方によってはまだ見ぬ模様になる可能性も多くあり、さらにグラフの範囲(コード内のhとv)を変更して拡大していくとさらなるフラクタル図形を確認できると思います。
是非本コードを使って遊んでみて下さい!
マンデルブロ集合も面白かったけど、ジュリア集合はさらに変化に富んでいて興味深かったです!
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています!

 ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!
ついにWATLABブログから書籍「いきなりプログラミングPython」が発売しました!