多次元解析チャートで3個以上の多変量グリッドサーチ結果を可視化

機械学習は多数のハイパーパラメータの組み合わせにより予測精度が決まります。ここではヒートマップでは表現出来ない3つ以上のパラメータとスコアの関係性可視化方法である多次元解析チャートをグリッドサーチの結果を使って紹介します。

こんにちは。wat(@watlablog)です。ここでは多変量分析で効果を発揮する多次元解析チャートの作り方を紹介します！

目次（項目クリックでジャンプできます）

多次元解析チャートの概要

多次元解析チャートとは？

多次元解析チャート(Multidimensional Analysis Chart)とは、複数の説明変数と1つまたは複数の目的変数で構成された、それぞれのパラメータを線で繋いだデータ可視化手法です。

下図が多次元解析チャートの例です。見せ方は色々あるようですが、今回Pythonコードで作成するのはこの図になります。

追記：平行座標プロットという呼び方もあるそうです。

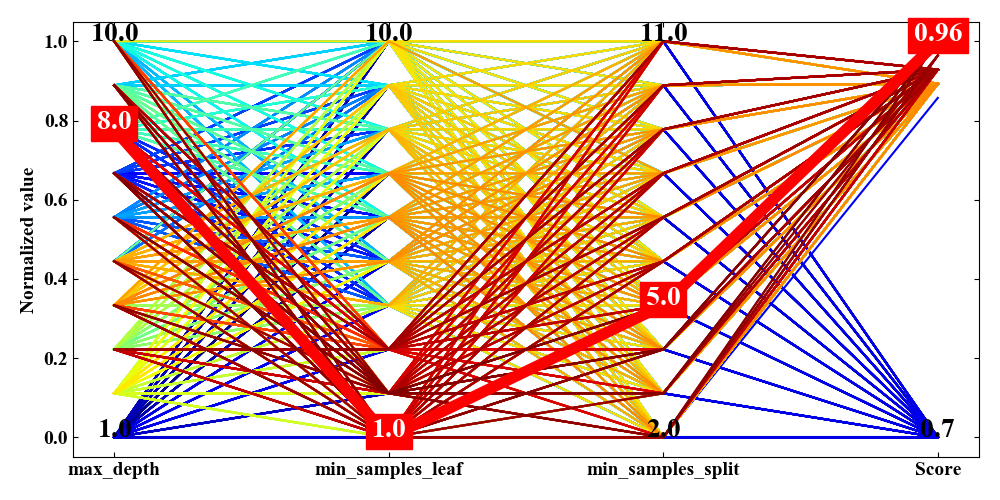
この図は横軸に変数名があり、左3つが説明変数、一番右側が目的変数です。

ちなみに、この変数群はscikit-learnに内蔵されているiris分類データセットを決定木モデルでグリッドサーチした結果です。

決定木については「Python/sklearnで決定木分析!分類木の考え方とコード」、
グリッドサーチについては「Pythonのグリッドサーチで決定木のハイパーパラメータを調整！」にそれぞれ詳細を記載しましたので、是非お読み頂ければと思います。

この多次元解析チャートには主に2つのメリットがありますので、以下に紹介します。

多次元解析チャートのメリット2選

説明変数と目的変数の組み合わせが一目瞭然となる

多次元解析チャートは複数のパラメータをどう調整したら良いか迷った時に重宝します。

scikit-learnに付属しているGridSearchCVは交差検証をしてくれたり、最適モデル(スコアの最も高いモデル)を自動的に抽出してくれたりと便利な機能が備わっていますが、機械学習モデルは訓練データでいくらスコアが良くても未知のデータでは使い物にならないといったことも十分考えられます。

このようなケースを過学習(オーバーフィッティング)と呼び、機械学習で最も注意しなければいけない要素になります。

先ほど紹介した図の線の色は目的変数であるScoreが高いと赤く、低いと青く、中間は黄色や緑というmatplotlibの「cmap='jet'」というカラーマップに対応しています。線に色付けすることで、目的変数が高くなる時はどういったパラメータの組み合わせを通って来たのかを視覚的に認識することができます。

例えば下図は赤く太い線がグリッドサーチが見つけてきた最適解（.best_estimator_）です。

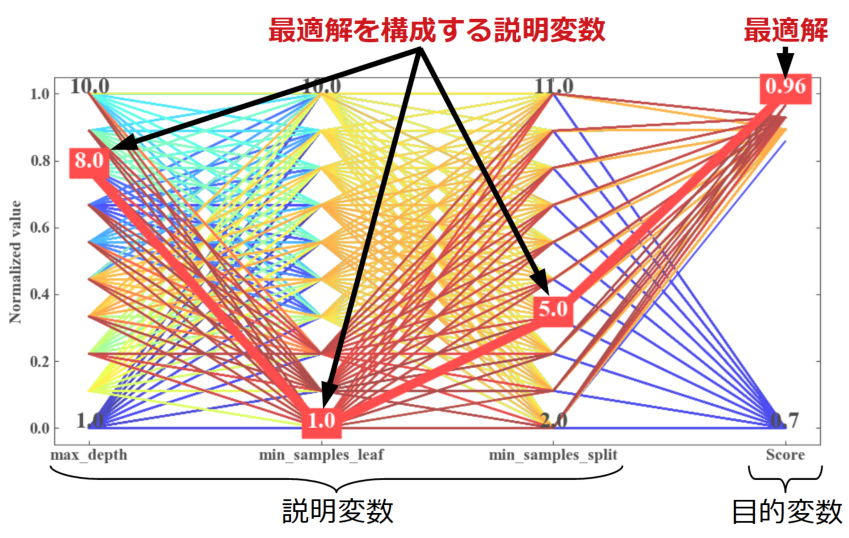
しかし決定木なのでノードの深さ(max_depth)が高く、1ノード(葉)に含まれる最小サンプル数(min_samples_leaf)が小さくなれば当然スコアが上がります。

決定木場合、できるだけシンプルな条件分岐や1ノードに多くのサンプルが含まれている方が、本質を抽出した学習モデルになったという事ができそうです。

今回の多次元解析チャートを見ると、最適解以外のパラメータの組み合わせ(通り道、パスと表現することも有り)も高スコアに繋がっていそうです。多次元解析チャートはこのようにデータの組み合わせを直感的に判断することが可能です。

絞込みで過学習を避けるパラメータセットを検討できる

決定木の場合は先ほど説明したように、過学習を軽減するためのパラメータの振り方はある程度人間が理解しやすいものです。

ここで、多次元解析チャートは「絞込み」という作業を行って、どの程度までスコアを維持しながらパラメータを変えることができるかを分析することも可能です。

下図が絞込みの例です。max_depthを小さく、min_samples_leafを大きくしてみると、スコアは0.03減少する程度ですがmax_depthを2まで少なくすることができました。

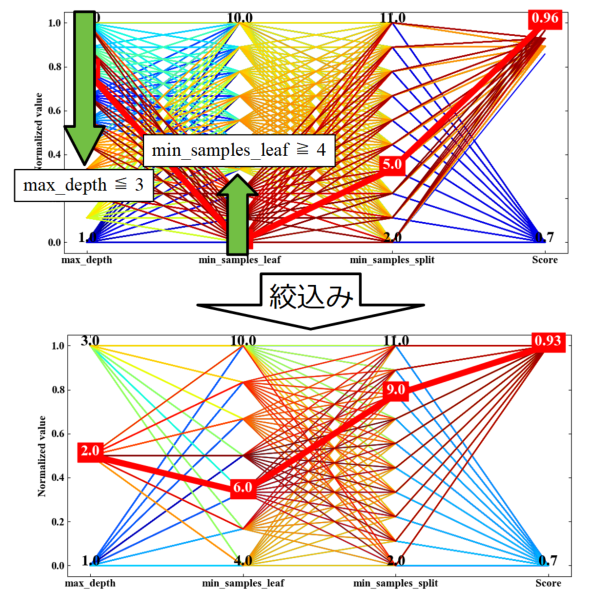
さらに絞込みとしてmin_samples_leafを大きくしていくと(下図)、スコアの変動は全く無いこともわかりました。

つまり、グリッドサーチ時のmin_samples_leafの値の設定範囲が全く意味を持っていなかったということが言えるのではないかと考えられます。

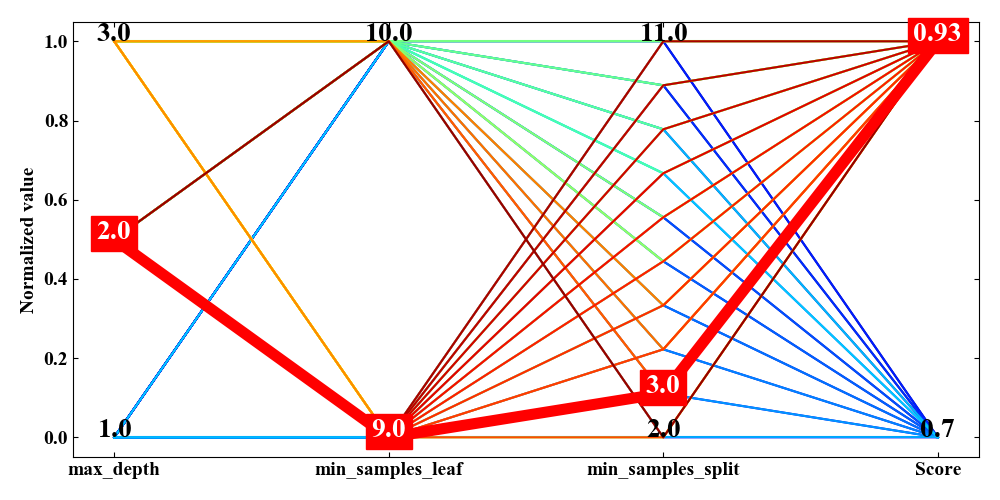
グリッドサーチに限らず、機械学習モデルの検証手法はエンジニアの設定次第でスコアが変動します。データの本質はどこにあるのかを分析する場合でも多次元解析チャートを眺めてみる価値があると言えます。

Pythonで多次元解析チャートを作るコード

フローチャート(簡易)

コードの説明の前に、ざっくりとですがこれから作るプログラムがどんなことをしているかを以下のフローチャートに示します。

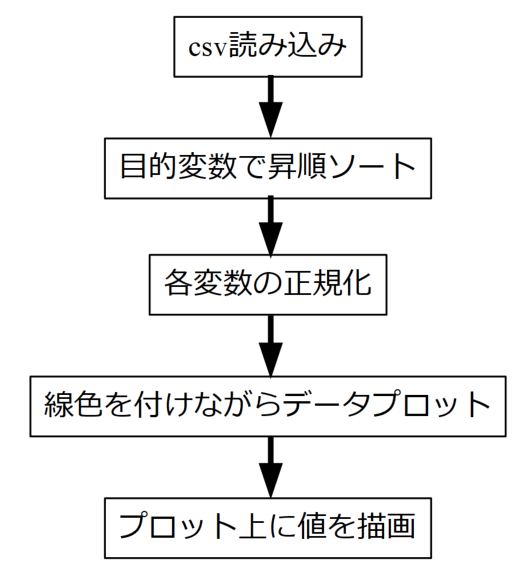
途中正規化(スケーリング)がありますが、この作業をしないと変数の桁が他と異なる場合にそれぞれの関係性がよくわからなくなってしまうために必要としています。

サンプルファイル

今回のプログラムコードは既にグリッドサーチを終えた状態からスタートします。

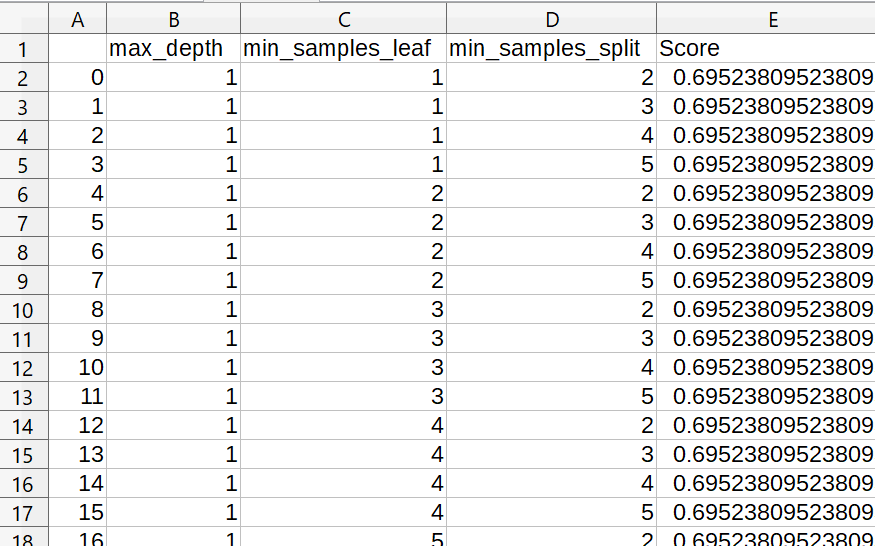
以下の図に示すSHIFT-JIS形式のcsvデータが必要ですが、前回の「Pythonのグリッドサーチで決定木のハイパーパラメータを調整！」のコードを一回流して頂ければこのファイルを作成することが可能ですので、多次元解析チャートをお試しで作成する場合にも参照してみて下さい。

※今回は前の記事よりも細かいグリッドを使っている点が異なります。

全コード

以下が多次元解析チャートの全サンプルコードです。詳細はコード内コメントの通りですが、10行目の絞込み部分はコメントアウト記号である「#」を外すことで機能します。

import pandas as pd
import numpy as np
from matplotlib import pyplot as plt

# csvファイルを読み込み(グリッドサーチ結果)
df = pd.read_csv('summary.csv', encoding='shift-jis',
                 index_col=0)
df = df.sort_values('Score', ascending=True)    # Score列で昇順ソート(高スコア値を最後にする）

# データ前処理(高スコアのデータのみ抽出)→下2行有効化で絞込みを実行
#df = df[df['min_samples_leaf'] >= 4.0]
#df = df[df['max_depth'] <= 3.0]

# プロットに必要な設定
n_col = len(df.columns)                         # 列数
n_row = len(df)                                 # 行数
maxs = np.zeros(n_col)                          # 正規化用最大値配列の初期化
mins = np.zeros(n_col)                          # 正規化用最小値配列の初期化
col = df.columns                                # 列名取得
cm = plt.get_cmap('jet', n_row)                 # jetのカラーマップを行数分の階調で用意
best = df.iloc[n_row - 1]                       # 最適解(正規化前)を抽出

# 各列を最大値と最小値で正規化
for i in range(n_col):
    maxs[i] = df.iloc[:, i].max()
    mins[i] = df.iloc[:, i].min()
    df.iloc[:, i] = (df.iloc[:, i] - mins[i]) / (maxs[i] - mins[i])

best_norm = df.iloc[n_row - 1]                  # 最適解(正規化後)を抽出

# グラフ描画事前設定-------------------------------------------------------------------------
# フォントの種類とサイズを設定する。
plt.rcParams['font.size'] = 14
plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。
plt.rcParams['xtick.direction'] = 'in'
plt.rcParams['ytick.direction'] = 'in'

# figureを定義する。
fig = plt.figure(figsize=(10, 5))

# グラフの上下左右に目盛線を付ける。
ax1 = fig.add_subplot(111)
ax1.yaxis.set_ticks_position('both')
ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。
ax1.set_ylabel('Normalized value')
# -------------------------------------------------------------------------------------------

# データプロット
for j in range(n_row):
    # プロットの最後(最高スコア)だけ赤太ラインにする
    if j == n_row - 1:
        ax1.plot(col, df.iloc[j], label=str(j), color='red', lw=8)
    # 他のデータは昇順ソートされているので、カラーマップの階調を順番に当てはめる
    else:
        ax1.plot(col, df.iloc[j], label=str(j), color=cm(j))
# 実際の値をプロット上に描画
for k in range(n_col):
    ax1.text(k, 1.0, str(round(maxs[k], 2)), fontsize=20, horizontalalignment='center')
    ax1.text(k, 0.0, str(round(mins[k], 2)), fontsize=20, horizontalalignment='center')
    ax1.text(k, best_norm[k], str(round(best[k], 2)),
             fontsize=20,
             color='white',
             backgroundcolor='red',
             horizontalalignment='center')

# グラフを表示する。
fig.tight_layout()
plt.show()
plt.close()

import pandas as pd

import numpy as np

from matplotlib import pyplot as plt

# csvファイルを読み込み(グリッドサーチ結果)

df = pd.read_csv('summary.csv', encoding='shift-jis',

index_col=0)

df = df.sort_values('Score', ascending=True) # Score列で昇順ソート(高スコア値を最後にする）

# データ前処理(高スコアのデータのみ抽出)→下2行有効化で絞込みを実行

#df = df[df['min_samples_leaf'] >= 4.0]

#df = df[df['max_depth'] <= 3.0]

# プロットに必要な設定

n_col = len(df.columns) # 列数

n_row = len(df) # 行数

maxs = np.zeros(n_col) # 正規化用最大値配列の初期化

mins = np.zeros(n_col) # 正規化用最小値配列の初期化

col = df.columns # 列名取得

cm = plt.get_cmap('jet', n_row) # jetのカラーマップを行数分の階調で用意

best = df.iloc[n_row - 1] # 最適解(正規化前)を抽出

# 各列を最大値と最小値で正規化

for i in range(n_col):

maxs[i] = df.iloc[:, i].max()

mins[i] = df.iloc[:, i].min()

df.iloc[:, i] = (df.iloc[:, i] - mins[i]) / (maxs[i] - mins[i])

best_norm = df.iloc[n_row - 1] # 最適解(正規化後)を抽出

# グラフ描画事前設定-------------------------------------------------------------------------

# フォントの種類とサイズを設定する。

plt.rcParams['font.size'] = 14

plt.rcParams['font.family'] = 'Times New Roman'

# 目盛を内側にする。

plt.rcParams['xtick.direction'] = 'in'

plt.rcParams['ytick.direction'] = 'in'

# figureを定義する。

fig = plt.figure(figsize=(10, 5))

# グラフの上下左右に目盛線を付ける。

ax1 = fig.add_subplot(111)

ax1.yaxis.set_ticks_position('both')

ax1.xaxis.set_ticks_position('both')

# 軸のラベルを設定する。

ax1.set_ylabel('Normalized value')

# -------------------------------------------------------------------------------------------

# データプロット

for j in range(n_row):

# プロットの最後(最高スコア)だけ赤太ラインにする

if j == n_row - 1:

ax1.plot(col, df.iloc[j], label=str(j), color='red', lw=8)

# 他のデータは昇順ソートされているので、カラーマップの階調を順番に当てはめる

else:

ax1.plot(col, df.iloc[j], label=str(j), color=cm(j))

# 実際の値をプロット上に描画

for k in range(n_col):

ax1.text(k, 1.0, str(round(maxs[k], 2)), fontsize=20, horizontalalignment='center')

ax1.text(k, 0.0, str(round(mins[k], 2)), fontsize=20, horizontalalignment='center')

ax1.text(k, best_norm[k], str(round(best[k], 2)),

fontsize=20,

color='white',

backgroundcolor='red',

horizontalalignment='center')

# グラフを表示する。

fig.tight_layout()

plt.show()

plt.close()

実行結果

上記コードを実行すると以下の結果を得ます。まずはフルデータの場合。

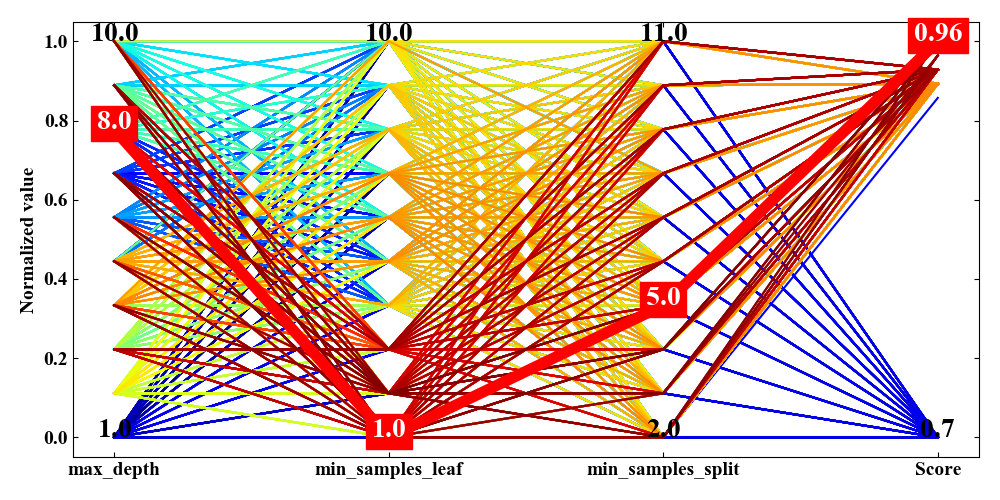
次に絞込みをした場合です。

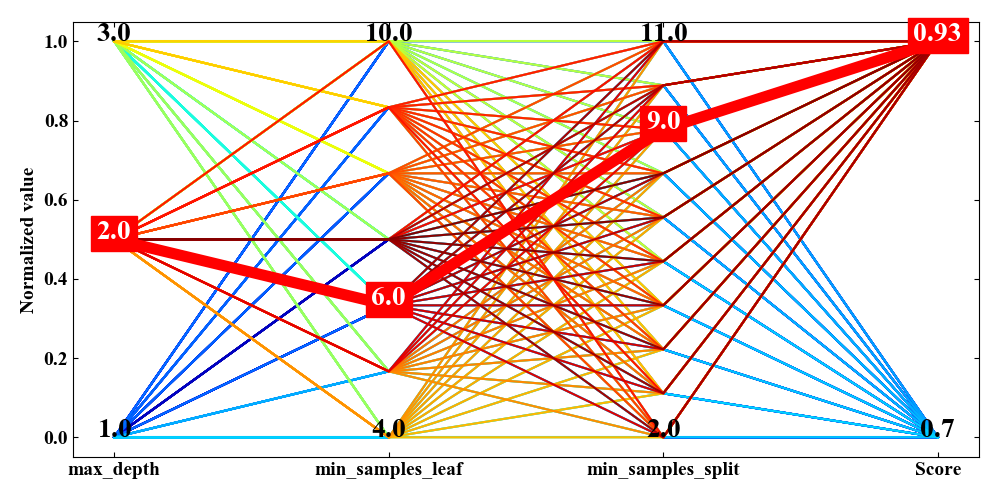
まとめ

本記事では多次元解析チャートの概要とメリットを説明し、Pythonコードを紹介しました。

scikit-learnのグリッドサーチをただ使っているだけでは、画面に最適スコア時のパラメータが見えるだけでしたが、多次元解析チャートを使って可視化を行うことで、各変数がどういった組み合わせの時にスコアが高くなるのかが一目瞭然でした。

また、このチャートを使うと変数の余裕度や検証ミスにも気付くことが出来そうです。

今後はグリッドサーチの条件を変えてみたり、機械学習モデルを変えてみたりしてデータ処理に慣れて行こうと思います。

多次元解析チャートは機械学習以外にも様々な多変量問題や最適化問題に活用が出来そうです！
Twitterでも関連情報をつぶやいているので、wat(@watlablog)のフォローお待ちしています！